Лекция
Привет, Вы узнаете о том , что такое оконное преобразование фурье, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое оконное преобразование фурье , настоятельно рекомендую прочитать все из категории Методы и средства компьютерных информационных технологий.
оконное преобразование фурье — это разновидность преобразования Фурье, определяемая следующим образом:
где — некоторая оконная функция. В случае дискретного преобразования оконная функция используется аналогично:
Существует множество математических формул, визуально улучшающих частотный спектр на разрыве границ окна. Для этого применяются преобразования: треугольное (Барлетта), синус-окно, синус в кубе, синус в 4-й степени, преобразование Парзена, Уэлча, Гаусса, Хеннинга, приподнятый косинус (Хэмминга), Чебышева, с пульсациями, Розенфилда, Блэкмана-Харриса, горизонтальное и с плоской вершиной. Также существует методика по взаимному перекрытию окон, при этом обычно можно выбрать сколько семплов из предыдущего окна будет усреднено с текущим окном.
На практике нет возможности получить сигнал на бесконечном интервале, так как нет возможности узнать, какой был сигнал до включения устройства и какой он будет в будущем. Ограничение интервала анализа равносильно произведению исходного сигнала на прямоугольную оконную функцию. Таким образом, результатом оконного преобразования Фурье является не спектр исходного сигнала, а спектр произведения сигнала и оконной функции. В результате возникает эффект, называемый растеканием спектра сигнала. Опасность заключается в том, что боковые лепестки сигнала более высокой амплитуды могут маскировать присутствие других сигналов меньшей амплитуды.
Для борьбы с растеканием спектра применяют более гладкую оконную функцию, спектр которой имеет более широкий главный лепесток и низкий уровень боковых лепестков. Спектр, полученный при помощи оконного преобразования Фурье, является сверткой спектра исходного идеального сигнала и спектра оконной функции.
Искажения, вносимые применением окон, определяются размером окна и его формой. Выделяют следующие основные свойства оконных функций: ширина главного лепестка по уровню -3 дБ, ширина главного лепестка по нулевому уровню, максимальный уровень боковых лепестков, коэффициент ослабления оконной функции.
Оконное преобразование Фурье применяется в связи для синтеза частотных фильтров, например, в методе частотного мультиплексирования с множеством несущих, использующим банк (гребенку) частотных фильтров FBMC .
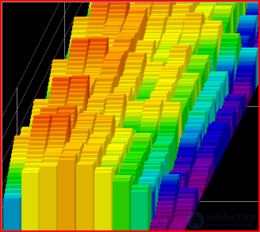
STFT используется для анализа аудиосигнала во времени.
STFT, а также стандартные преобразования Фурье и другие инструменты часто используются для анализа музыки. Спектрограмма может, например, отображать частоту на горизонтальной оси: самые низкие частоты слева, а самые высокие справа. Высота каждой полосы (дополненной цветом) представляет амплитуду частот в этом диапазоне. Измерение глубины представляет собой время, когда каждый новый столбец представлял собой отдельное преобразование. Аудиоинженеры используют этот вид визуальных эффектов для получения информации об аудиообразце, например, для определения частот определенных шумов (особенно при использовании с более высоким частотным разрешением) или для поиска частот, которые могут быть более или менее резонансными в пространстве, где находится сигнал был записан. Эту информацию можно использовать для эквалайзера или настройки других звуковых эффектов.
| Метод | Сложность |
|---|---|
| Прямая реализация | О(ТФвопрос) |
| на основе БПФ | О(ТНбревно2Н) |
| Рекурсивный | О(ТФ) |
| Чирп-Z-преобразование | О(ТНбревно2Н) |
При использовании оконного преобразования Фурье невозможно одновременно обеспечить хорошее разрешение по времени и по частоте. Об этом говорит сайт https://intellect.icu . Чем уже окно, тем выше разрешение по времени и ниже разрешение по частоте.

Сравнение оконного преобразования Фурье с разными окнами. Слева (узкое окно) - хорошее разрешение по времени, справа (более широкое окно) - хорошее разрешение по частоте.
Разрешение по осям является постоянным. Это нежелательно для ряда задач, в которых информация по частотам распределена неравномерно. В таких задачах в качестве альтернативы оконному преобразованию Фурье может использоваться вейвлет-преобразование, временное разрешение которого увеличивается с частотой (частотное снижается).

Прямоугольное окно; B=1.00
Получается автоматически при ограничении выборки N отсчетами. Максимальный уровень боковых лепестков частотной характеристики: -13 дБ.

Окно Ханна; B = 1.50
где N — ширина окна. Уровень боковых лепестков: −31.5 дБ.

Окно Хэмминга
Уровень боковых лепестков: -42 дБ.

Окно Блэкмана; α = 0.16; B=1.73
Уровень боковых лепестков: -58 дБ (α=0.16).
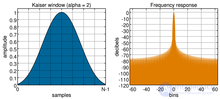
Окно Кайзера, α =2; B=1.5

Окно Кайзера, α =3; B=1.8
где 0 — модифицированная функция Бесселя первого рода нулевого порядка;
— коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции. Чем больше
тем больше доля энергии, и шире главный лепесток, и меньше уровень боковых лепестков. На практике используются значения от 4 до 9.
Для оконного преобразования Фурье в цифровом виде может применяться не только взвешивание каждого цифрового отсчета в процессе формирования свертки, но и эквивалентное весовое суммирование откликов преобразования Фурье .
К примеру взвешивание окном Ханна (Хеннинга) и окном Хэмминга может быть представлено в виде:
,
где ,
,
- исходные отклики преобразования Фурье,
- результат оконного преобразования,
соответствует окну Ханна (Хеннинга),
- окну Хэмминга .
Реализация указанного взвешивания осуществляется в режиме скользящего окна по массиву откликов преобразования Фурье.
Исследование, описанное в статье про оконное преобразование фурье, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое оконное преобразование фурье и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Методы и средства компьютерных информационных технологий
Из статьи мы узнали кратко, но содержательно про оконное преобразование фурье
Комментарии
Оставить комментарий
Методы и средства компьютерных информационных технологий
Термины: Методы и средства компьютерных информационных технологий