Лекция
Привет, Вы узнаете о том , что такое преобразование фурье для одномерного сигнала, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое преобразование фурье для одномерного сигнала, свойства преобразования фурье , настоятельно рекомендую прочитать все из категории Методы и средства компьютерных информационных технологий.
Преобразование Фурье (символ ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.Названо в честь Фурье, Жан-Батист Жозеф
Преобразование Фурье позволяет представить практически любую функцию или набор данных в виде комбинации таких тригонометрических функций, как синус и косинус, что позволяет выявить периодические компоненты в данных и оценить их вклад в структуру исходных данных или форму функции. Традиционно различаются три основные формы преобразования Фурье: интегральное преобразование Фурье, ряды Фурье и дискретное преобразование Фурье.
Интегральное преобразование Фурье переводит вещественную функцию в пару вещественных функций или одну комплексную функцию в другую.
Вещественную функцию f(x) можно разложить по ортогональной системе тригонометрических функций, то есть представить в виде

где A(ω) и B(ω) называются интегральными косинус- и синус-преобразованиями:
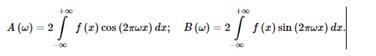
Ряд Фурье представляет периодическую функцию f(x), заданную на интервале [a,b], в виде бесконечного ряда по синусам и косинусам. То есть периодической функции f(x) ставится в соответствие бесконечная последовательность коэффициентов Фурье
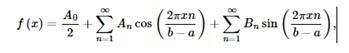
где
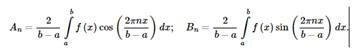
Дискретное преобразование Фурье переводит конечную последовательность вещественных чисел в конечную последовательность коэффициентов Фурье.
Пусть {xi},i=0,…,N−1 - последовательность вещественных чисел - например, отсчеты яркости пикселов по строке изображения. Эту последовательность можно представить в виде комбинации конечных сумм вида
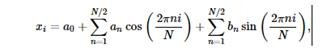
где
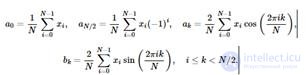
Основное отличие между тремя формами преобразования Фурье заключается в том, что если интегральное преобразование Фурье определено по всей области определения функции f(x), то ряд и дискретное преобразование Фурье определены только на дискретном множестве точек, бесконечном для ряда Фурье и конечном для дискретного преобразования.
Как видно из определений преобразования Фурье, наибольший интерес для систем цифровой обработки сигналов представляет дискретное преобразование Фурье. Данные, получаемые с цифровых носителей или источников информации, представляют собой упорядоченные наборы чисел, записанные в виде векторов или матриц.
Обычно принимается, что входные данные для дискретного преобразования представляют собой равномерную выборку с шагом Δ, при этом величина T=NΔ называется длиной записи, или основным периодом. Основная частота равна 1/T. Таким образом, в дискретном преобразовании Фурье производится разложение входных данных по частотам, которые являются целым кратным основной частоты. Максимальная частота, определяемая размерностью входных данных, равна 1/2Δ и называется частотойНайквиста. Учет частоты Найквиста имеет важное значение при использовании дискретного преобразования. Если входные данные имеют периодические составляющие с частотами, превышающими частоту Найквиста, то при вычислении дискретного преобразования Фурье произойдет подмена высокочастотных данных более низкой частотой, что может привести к ошибкам при интерпретации результатов дискретного преобразования.
Важным инструментом анализа данных является также энергетическийспектр. Мощность сигнала на частоте ω определяется следующим образом:
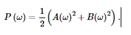
Эту величину часто называют энергиейсигнала на частоте ω. Согласно теореме Парсеваля общая энергия входного сигнала равна сумме энергий по всем частотам.
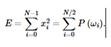
График зависимости мощности от частоты называется энергетическим спектром или спектром мощности. Энергетический спектр позволяет выявлять скрытые периодичности входных данных и оценивать вклад определенных частотных компонент в структуру исходных данных.
Свойствами преобразований Фурье определяется взаимное соответствие трансформации сигналов и их спектров.
1. Линейность. Преобразование Фурье относится к числу линейных интегральных операций, т.е. спектр суммы сигналов равен сумме спектров этих сигналов.
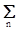 ansn(t) <=>
ansn(t) <=> 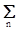 anSn(w). (4.3.1)
anSn(w). (4.3.1)
Пример суммирования сигналов и его отображения в спектральной области на рис. 4.3.1.
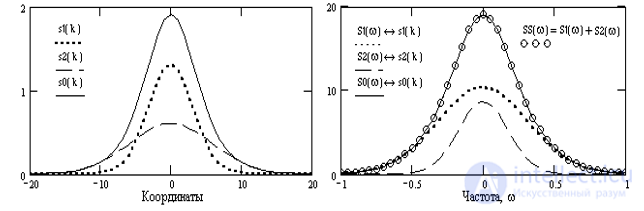
Рис. 4.3.1. Сигналы и их спектры. s0(k)=s1(k)+s2(k) <=>S1(w)+S2(w) = S0(w).
.
|
Сигнал s(t) |
Спектр S(w) |
|
Четный |
Вещественный, четный |
|
Нечетный |
Мнимый, нечетный |
|
Произвольный |
Действительная часть – четная. Мнимая часть - нечетная |
2. Свойства симметрии преобразования определяются косинусными (четными, действительными) и синусными (нечетными, мнимыми) частями разложения и подобием прямого и обратного преобразований.
На рис. 4.3.2. приведены примеры, поясняющие свойства четности преобразования. Сигнал s1(k) является четным, s1(k) = s1(-k), и имеет только вещественный четный спектр (мнимая часть спектральной функции представлена нулевыми значениями). Сигнал s2(k) = -s2(-k) нечетный и имеет мнимый нечетный спектр, а нулевыми значениями представлена его действительная часть. Сигнал s3(k) образован суммой сигналов s1(k) и s2(k). Соответственно, спектральная функция сигнала представлена и действительной четной частью (принадлежащей s1(k)), и мнимой нечетной частью (принадлежащей s2(k)). При обратном преобразовании Фурье раздельно действительной и мнимой части спектра S3(w), равно как и любых других комплексных спектров, будут раздельно восстановлены четная и нечетная части исходного сигнала.
Произвольный исходный сигнал может быть задан в одностороннем варианте (0-Т), но четная и нечетная части этого сигнала занимают интервал от –Т до Т, при этом на левой половине числовой оси (от –Т до 0) эти два сигнала компенсируют друг друга, давая нулевые значения.
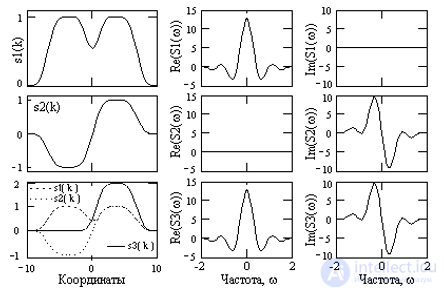
Рис. Об этом говорит сайт https://intellect.icu . 4.3.2. Свойства четности преобразования.
3. Изменение аргумента функции (сжатие или расширение сигнала) приводит к обратному изменению аргумента ее фурье-образа и обратно пропорциональному изменению его модуля. Так, если s(t) Û S(w), то при изменении длительности сигнала с сохранением его формы (растяжении сигнала по временной оси), т.е. для сигнала с новым аргументом s(x) = s(at) при x=at, получаем:
s(at) <=> 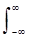 s(at)exp(-jwt) dt = (1/a)
s(at)exp(-jwt) dt = (1/a)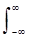 s(x)exp(-jxw/a) dx
s(x)exp(-jxw/a) dx
s(at) <=> (1/a) S(w/a). (4.3.2')
Выражение (4.3.2') действительно при а>0. При а<0 происходит зеркальный поворот сигнала относительно вертикальной оси, а замена переменной t=x/a вызывает перестановку пределов интегрирования и, соответственно, изменение знака спектра:
s(at) <=> -(1/a) S(w/a). (4.3.2'')
Обобщенная формула изменения аргумента:
s(at) <=> (1/|a|) S(w/a), a ≠ 0 (4.3.2)
Если под аргументом функции и ее спектра понимать определенные физические единицы, например, время - частота, то отсюда следует: чем короче по своей длительности сигнал, тем шире по частоте его спектр, и наоборот. Это можно наглядно видеть на рис. 4.3.1. для сигналов s1(k) и s2(k) и их спектров S1(w) и S2(w).
От изменения аргумента функций следует отличать изменение масштаба представления функций. Изменение масштаба аргументов изменяет оцифровку числовых осей отображения сигналов и их спектров, но не изменяет самих сигналов и спектров. Так, при масштабе оси времен t=1 секунда, масштаб оси частот f=1/t=1 герц, а при t=1 мксек f=1/t=1 МГц (t=at, f=1/at, a=10-6).'
4. Теорема запаздывания. Запаздывание (сдвиг, смещение) сигнала по аргументу функции на интервал to приводит к изменению фазочастотной функции спектра (фазового угла всех гармоник) на величину -wto. Применяя замену переменной t-to = x, получаем:
s(t-to) <=>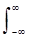 s(t-to)exp(-jwt) dt =
s(t-to)exp(-jwt) dt =
=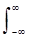 s(x)exp(-jwx)exp(-jwto) dx = S(w)exp(-jwto). (4.3.3)
s(x)exp(-jwx)exp(-jwto) dx = S(w)exp(-jwto). (4.3.3)
Совершенно очевидно, что амплитуды гармоник сигнала при его сдвиге изменяться не должны. С учетом того, что |exp(-jwto)|=1, это следует и из (4.3.3):
|S(w) exp(-jwto)| = |S(w)|.
Фазовый спектр сдвигается на -wto с линейной зависимостью от частоты:
S(w) exp(-jwto)= R(w) exp[j(j(w)]exp(-jwto)= R(w) exp[j(j(w)-wto)]. (4.3.4)
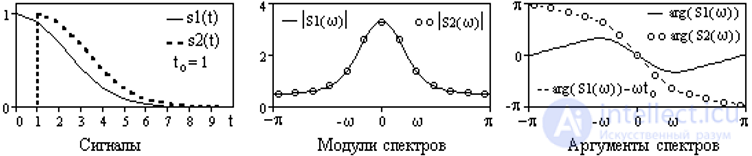
Рис. 4.3.3. Изменение спектра сигнала при его сдвиге.
Пример двух одинаковых сигналов, сдвинутых относительно друг друга на to=1, и соответствующих данным сигналам спектров приведен на рис. 4.3.3.
Аналогично нетрудно показать, что сдвиг спектра в частотной области на w0 вызывает умножение сигнала на exp(jw0t):
S(w - w0) <=> s(t) exp(jw0t),
что эквивалентно модуляции сигнала функцией комплексной экспоненты во временной области.
5. Преобразование производной (дифференцирование сигнала):
s(t) = d[y(t)]/dt = d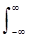 [Y(w) exp(jwt) dw]/dt =
[Y(w) exp(jwt) dw]/dt =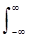 Y(w) [d(exp(jwt))/dt] dw =
Y(w) [d(exp(jwt))/dt] dw =
= 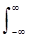 jw Y(w) exp(jwt) dw <=> jw Y(w). (4.3.5)
jw Y(w) exp(jwt) dw <=> jw Y(w). (4.3.5)
Дифференцирование сигнала отображается в спектральной области простым умножением спектра сигнала на оператор дифференцирования сигнала в частотной области jw, что эквивалентно дифференцированию каждой гармоники спектра. Умножение на jw приводит к обогащению спектра производной сигнала высокочастотными составляющими (по сравнению с исходным сигналом) и уничтожает составляющие с нулевой частотой.
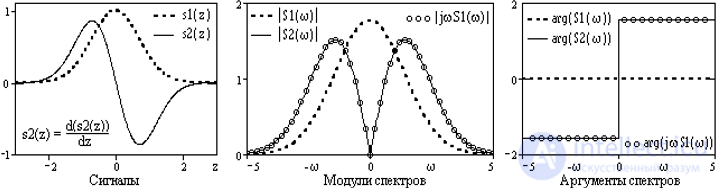
Рис. 4.3.4. Спектры сигнала и его производной.
Пример сигнала, его производной и соответствующих им спектров приведен на рис. 4.3.4. По изменению аргумента спектра (для четного исходного сигнала он был нулевым) можно видеть, что для всех гармоник спектра появляется сдвиг фаз на p/2 (900) для положительных частот, и на -p/2 (-900) для отрицательных частот.
В общем случае, для кратных производных:
dn[y(t)]/dtn = (jw)n Y(w). (4.3.6)
При дифференцировании спектра функции соответственно получаем:
dn[S(w)]/dwn = (-jt)n s(t).
6. Преобразование интеграла сигнала в частотной области при известном спектре сигнала может быть получено из следующих простых соображений. Если имеет место
s(t) = d[y(t)]/dt Û jw Y(w) = S(w),
то должна выполняться и обратная операция: y(t) =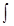 s(t) dt <=> Y(w) = S(w)/jw. Отсюда следует:
s(t) dt <=> Y(w) = S(w)/jw. Отсюда следует:
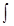 s(t)dt <=> (1/jw)S(w). (4.3.7)
s(t)dt <=> (1/jw)S(w). (4.3.7)
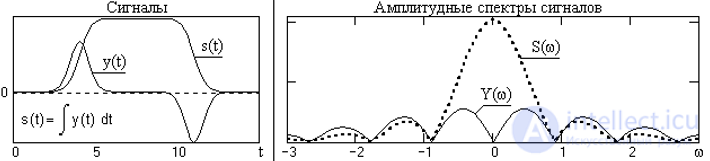
Рис. 4.3.5. Сигналы и амплитудные спектры сигналов.
Оператор интегрирования в частотной области (1/jw) при w>1 ослабляет в амплитудном спектре высокие частоты и при w<1 усиливает низкие. Фазовый спектр сигнала смещается на -900для положительных частот и на 900 для отрицательных. Пример модуля спектра сигнала и его интегральной функции приведен на рис. 4.3.5.
Формула (4.3.7) справедлива для сигналов с нулевой постоянной составляющей. При интегрировании сигналов с определенным значением постоянной составляющей С=const в правой части выражения (4.3.7) появляется дополнительное слагаемое преобразования Фурье постоянной составляющей C, которое представляет собой дельта-функцию на нулевой частоте с весовым коэффициентом, равным значению С:
(1/jw)S(w) + C·d(0).
7. Преобразование свертки сигналов y(t) = s(t) * h(t):
Y(w) =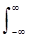 y(t) exp(-jwt) dt =
y(t) exp(-jwt) dt =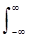
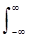 s(t) h(t-t) exp(-jwt) dtdt.
s(t) h(t-t) exp(-jwt) dtdt.
Y(w) =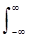 s(t) dth(t-t) exp(-jwt) dt.
s(t) dth(t-t) exp(-jwt) dt.
По теореме запаздывания (4.3.3):
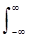 h(t-t) exp(-jwt) dt = H(w) exp(-jwt).
h(t-t) exp(-jwt) dt = H(w) exp(-jwt).
Отсюда: Y(w) =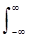 H(w) s(t) exp(-jwt) dt = H(w)·S(w).
H(w) s(t) exp(-jwt) dt = H(w)·S(w).
s(t) * h(t) <=> S(w) H(w). (4.3.8)
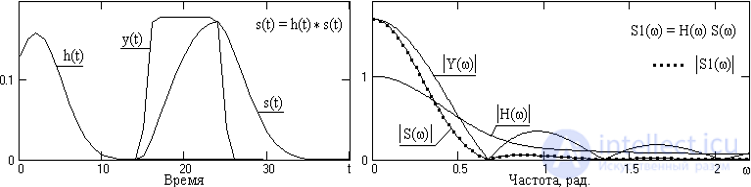
Рис. 4.3.6. Сигналы и амплитудные спектры сигналов.
Пример выполнения свертки в частотной области приведен на рис. 4.3.6. Отметим, что частотное представление H(w) импульсного отклика h(t) линейной системы (или соответствующей линейной операции) имеет смысл частотной передаточной функции системы и позволяет определить сигнал на выходе системы (в частотной форме представления) при задании произвольного сигнала (в частотной форме) на ее входе. По существу, функция H(w) представляет собой распределение по частоте коэффициента пропускания частотных составляющих сигнала с входа на выход системы.
Таким образом, свертка функций в координатной форме отображается в частотном представлении произведением фурье-образов этих функций.
Это положение имеет фундаментальное значение в практике обработки данных.
Любая линейная система обработки данных (информационных сигналов) реализует определенную операцию трансформации сигнала, т.е. выполняет операцию свертки входного сигнала s(t) с оператором системы h(t). С использованием преобразования свертки эта операция может производиться как с динамической, так и с частотной формой представления сигналов. При этом обработка данных, представленных в цифровой форме, производится, как правило, в частотной области, т.к. может быть на несколько порядков выше по производительности, чем во временной области. Она представляет собой последовательность следующих операций.
1. Перевод сигнала в частотную область: s(t) Û S(w).
2. Умножение спектра сигнала на передаточную функцию системы: Y(w) = H(w)·S(w).
Передаточная функция системы определяется аналогичным преобразованием h(t) Û H(w) или задается непосредственно в частотном представлении, что позволяет задавать передаточные функции сколь угодно сложной формы, в том числе с разрывами и скачками, для которых во временной области потребуются операторы h(t) с бесконечной импульсной характеристикой.
3. Перевод спектра обработанного сигнала во временную область: Y(w) Û y(t).
8. Преобразование произведения сигналов y(t) = s(t)·h(t):
Y(w) =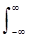 s(t) h(t) exp(-jwt) dt =
s(t) h(t) exp(-jwt) dt =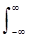 s(t) [(1/2p)
s(t) [(1/2p)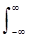 H(w') exp(jw't) dw'] dt =
H(w') exp(jw't) dw'] dt =
= (1/2п)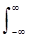
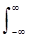 s(t)H(w') exp(-j(w-w')t) dw'dt =
s(t)H(w') exp(-j(w-w')t) dw'dt =
(1/2п)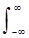 H(w') dw's(t)
H(w') dw's(t) 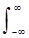 exp(-j(w-w')t) dt =
exp(-j(w-w')t) dt =
= (1/2п)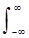 H(w') S(w-w') dw' = (1/2п) H(w) * S(w). (4.3.9)
H(w') S(w-w') dw' = (1/2п) H(w) * S(w). (4.3.9)
Таким образом, произведение функций в координатной форме отображается в частотном представлении сверткой фурье-образов этих функций, с нормировочным множителем (1/2p), учитывающем несимметричность прямого и обратного преобразования Фурье функций s(t) и h(t) при использовании угловых частот.
9. Производная свертки двух функций s'(t) = d[x(t) * y(t)]/dt. С использованием выражений (4.3.6) и (4.3.8), получаем:
s'(t) = jw [X(w) Y(w)] = (jw X(w)) Y(w) = X(w) (jw Y(w).
s'(t) = x'(t) * y(t) = x(t) * y'(t).
Это выражение позволяет выполнять вычисление производной сигнала с одновременным сглаживанием весовой функцией, которая является производной сглаживающей функции (например, гауссиана).
10. Спектры мощности. Временная функция мощности сигнала в общей форме определяется выражением:
w(t) = s(t) s*(t) = |s(t)|2.
Спектральная плотность мощности, соответственно, равна преобразованию Фурье произведения s(t)·s*(t), которое отобразится в спектральном представлении сверткой Фурье-образов этих функций:
W(f) = S(f) * S*(f) =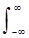 S(f) S*(f-v) dv. (4.3.10)
S(f) S*(f-v) dv. (4.3.10)
Но для всех текущих значений частоты f интеграл в правой части этого выражения равен произведению S(f)·S*(f), так как для всех значений сдвига v ≠ 0 в силу ортогональности гармоник S(f) и S*(f-v) значения их произведения равны нулю. Отсюда:
W(f) = S(f) * S*(f) = |S(f)|2. (4.3.11)
Спектр мощности - вещественная неотрицательная четная функция, которую очень часто называют энергетическим спектром. Спектр мощности, как квадрат модуля спектра сигнала, не содержит фазовой информации о частотных составляющих, а, следовательно, восстановление сигнала по спектру мощности невозможно. Это означает также, что сигналы с различными фазовыми характеристиками могут иметь одинаковые спектры мощности. В частности, сдвиг сигнала не отражается на его спектре мощности.
Для функций мощности взаимодействия сигналов в частотной области соответственно имеем частотные спектры мощности взаимодействия сигналов:
Wxy(f) = X(f) Y*(f),
Wyx(f) = Y(f) X*(f),
Wxy(f) = W*yx(f).
Функции мощности взаимодействия сигналов комплексные, даже если обе функции x(t) и y(t) вещественны, при этом Re[Wxy(f)] - четная функция, а Im[Wxy(f)] - нечетная. Отсюда полная энергия взаимодействия сигналов при интегрировании функций мощности взаимодействия определяется только реальной частью спектра:
Exy = (1/2п)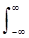 Wxy(w) dw = (1/п)
Wxy(w) dw = (1/п)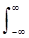 Re[Wxy] dw,
Re[Wxy] dw,
и всегда является вещественным числом.
11. Равенство Парсеваля. Полная энергия спектра сигнала:
Es =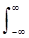 W(f) df =
W(f) df =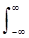 |S(f)|2 df. (4.3.12)
|S(f)|2 df. (4.3.12)
Так как координатное и частотное представление по существу только разные математические отображения одного и того же сигнала, то равной должна быть и энергия сигнала в двух представлениях, откуда следует равенство Парсеваля:
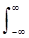 |s(t)|2 dt =
|s(t)|2 dt =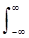 |S(f)|2 df,
|S(f)|2 df,
т.е. энергия сигнала равна интегралу модуля его частотного спектра - сумме энергий всех частотных составляющих сигнала. Аналогично для энергии взаимодействия сигналов:
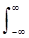 x(t) y*(t) dt =
x(t) y*(t) dt =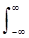 X(f) Y*(f) df.
X(f) Y*(f) df.
Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:
áx(t),y(t)ñ = áX(f),Y(f)ñ, ||x(t)||2 = ||X(f)||2.
Не следует забывать, что при представлении спектров в круговых частотах (по w) в правой части приведенных равенств должен стоять множитель 1/2п.
Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть обратимый переход от временно́го пространства в частотное пространство. Богатые возможности применения основываются на нескольких полезных свойствах преобразования:
В заключение, эта статья об преобразование фурье для одномерного сигнала подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое преобразование фурье для одномерного сигнала, свойства преобразования фурье и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Методы и средства компьютерных информационных технологий
Комментарии
Оставить комментарий
Методы и средства компьютерных информационных технологий
Термины: Методы и средства компьютерных информационных технологий