Кратковременное преобразование Фурье одномерного сигнала. Частотно-временной анализ сигналов. кратко

Привет, Вы узнаете о том , что такое кратковременное преобразование фурье, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое кратковременное преобразование фурье, частотно-временной анализ сигналов , настоятельно рекомендую прочитать все из категории Методы и средства компьютерных информационных технологий.

классическое преобразование Фурье (непрерывное и дискретное) является весьма полезным математическим аппаратом для анализа и синтеза сигналов, однако иногда оказывается недостаточно эффективным при обработке сложных сигналов. Преобразование Фурье, например, не отличает сигналы из двух синусоид с разными частотами, один из которых представляет собой сумму синусоид, второй – последовательно следующие друг за другом синусоиды. В обоих случаях их спектр будет выглядеть как

два пика на двух фиксированных частотах. Следовательно, преобразование Фурье в своем традиционном виде не приспособлено для анализа нестационарных сигналов в том числе локализованных на некотором временном интервале, так как теряется информация о временных характеристиках сигнала.

Следовательно, спектральный анализ реальных сигналов необходимо осуществлять как по частоте, так и во времени. Преимущества такого анализа очевидны. Об этом говорит сайт https://intellect.icu . На практике чаще всего приходится иметь дело с нестационарными процессами, в которых информативным является сам факт изменения частотно-временных характеристик сигнала

Для выполнения такого анализа требуются базисные функции, обладающие способностью выявлять в анализируемом сигнале как частотные, так и его временные характеристики. Другими словами, сами базисные функции должны обладать определенными

свойствами, названными частотно - временной локализацией

3.1. Частотно-временные свойства базисных функций

3.1.1. Плоскость частота-время

Для анализа и сравнения частотно-временных локализационных свойств различных базисов используют плоскость частота-время. Любая функция ϕ(t) может характеризоваться интервалом на временной оси и интервалом в Фурье области, в которых содержится 90% ее энергии, сосредоточенной около центра тяжести (В.3) функции . Тогда в этой плос- кости функцию ϕ (t) можно изобразить в виде прямоугольника, как показано на рис. 3.1. Очевидно, что смещение функции на τ от исходного состояния вызо- вет перемещение прямоугольника параллельно оси t .

Как следует из свойства масштабирования Фурье-преобразования(2.2.5), ширина базисной функции во временной и частотной областях взаимосвязаны: расширение функции во временной области ведет к ее сужению в частотной и наоборот.

Закономерность, связывающая две эти величины, называется принципом неопределенности

Итак, частотно-временной анализ предназначен для выявления локальных частотно-временных возмущений сигнала. Вследствие кратковре- менности таких возмущений, сам сигнал может рассматриваться как заданный в L2 , т.е. для одномерных сигналов – на всей действительной оси R(− ∞,∞) с нормой

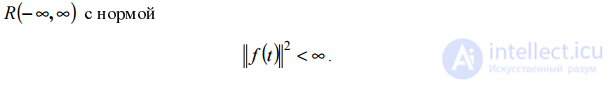
Следовательно, базисные функции, которые получили название вейвлетов, также должны принадлежать L2 и быстро убывать при t → ∞ . Тогда, чтобы перекрыть такими базисными функциями все возможные временные положения сигнала, необходимо, чтобы базисные функции представляли собой набор смещенных во времени функций. Удобнее всего, если этот набор образуется из одной и той же "материнской" функции ψ (t) (прототипа), сдвинутой по оси t , т.е. { ψ(t − b). } Чтобы обеспечить частотный анализ, базисная функция должна иметь еще один аргумент – масштабный коэффициент, который является аналогом частоты в Фурье- анализе. Тогда базисные функции для частотно-временного анализа будут меть вид

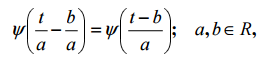
В заключение, эта статья об кратковременное преобразование фурье подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое кратковременное преобразование фурье, частотно-временной анализ сигналов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Методы и средства компьютерных информационных технологий

Из статьи мы узнали кратко, но содержательно про кратковременное преобразование фурье