12. Анализ речевых сигналов в частотной области. Гомоморфная обработка речи

Привет, Вы узнаете о том , что такое анализ речевых сигналов в частотной области гомоморфная обработка речи, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое анализ речевых сигналов в частотной области гомоморфная обработка речи , настоятельно рекомендую прочитать все из категории Методы и средства компьютерных информационных технологий.

Одним из основных способов обработки речи в частотной области является кратковременный спектральный анализ. На выполнении кратковременного спектрального анализа основана работа многих систем распознавания речи, спектрографов, вокодеров. Кратковременный спектральный анализ может быть реализован с использованием гребенки полосовых фильтров (рис. 2) или с помощью дискретного преобразования Фурье. Полосы пропускания фильтров выбираются так, чтобы перекрыть весь частотный диапазон речи. Средние значения модулей выходных сигналов фильтров будут представлять значения спектральных коэффициентов в полосах.

 

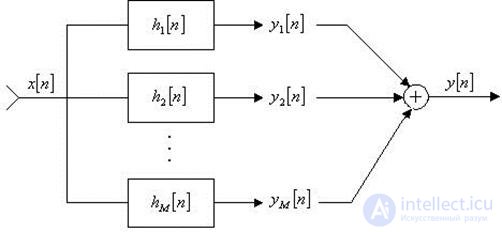
Рис. 2. Гребенка фильтров.

 Иногда частотный диапазон разбивают на неравные полосы с учетом особенностей слухового восприятия человека. Экспериментально установлено, что во внутреннем ухе человека высота тона (частота) звукового сигнала преобразуется в механические колебания определенных участков базилярной мембраны. При этом линейным приращениям координаты вдоль тела мембраны соответствуют логарифмические приращения частоты звука, т.е. частота звука, воспринимаемого человеком, нелинейно зависит от действительной физической частоты. Это приводит к неодинаковой разрешающей способности по частоте и к восприятию звуков в соответствии смеханизмом критических частотных полос. Сложный звук постоянной громкости, состоящий из нескольких тонов, лежащих в пределах критической полосы, воспринимается человеком с таким же субъективным ощущением, как одно-тональный звук, соответствующий центральной частоте критической полосы. Ширина критических полос для области частот до 500  Гц составляет примерно 100  Гц. Выше 500 Гц ширина критических полос увеличивается примерно на  20% по сравнению с шириной предыдущей полосы. Ширина критических полос аппроксимируется зависимостью: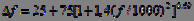 

 [Гц].

Для характеристики субъективных частот, воспринимаемых человеком, предложено несколько шкал: барк-шкала, мел-шкала. Функция

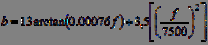 [Барк]

используется для перевода частот, заданных в герцах, в барки.

Гребенка (банк) фильтров с неравными полосами пропускания, заданными в герцах и соответствующими критическим полосам слуха, будет иметь равномерное распределение центральных частот и равные значения полос пропускания, измеренных в барках. Таким образом, применение барк-шкалы соответствует равномерному разбиению оси субъективных частот. Мел-шкала вводится с аналогичной целью и имеет незначительные отличия от барк-шкалы.

Кратковременный спектральный анализ речи может быть также выполнен на основе ДПФ. Кратковременное дискретное преобразование Фурьеопределяется следующим образом:

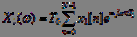 , (3)

где   представляет отрезок речи, взвешенный окном   , длиной 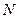 отсчетов:

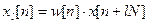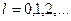 ,  . (4)

Один из алгоритмов определения частоты основного тона основан на вычислении произведения:

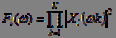   . Об этом говорит сайт https://intellect.icu . (5)

Значения, вычисляемые с помощью (5), могут быть весьма большими. Для уменьшения значений вычисляют логарифм от (5). Зависимость  представляет произведение функций  , сжатых по частоте. В вокализованной речи сжатие частоты в  раз должно привести к совпадению гармоник основного тона. Благодаря этому в спектре  появляется максимум на частоте основного тона. Невокализованная речь характеризуется существенно меньшими значениями  и она не имеет максимума в спектре  на частоте основного тона. Данный способ определения частоты основного тона устойчив к шумам, поскольку шумовые компоненты в спектре  не регулярны.

Гомоморфная обработка речи.

Речевой сигнал является сверткой функции возбуждения (случайного шума либо квазипериодической последовательности импульсов) и импульсной характеристики голосового тракта. Гомоморфный анализ речи позволяет разделить эти компоненты. Поэтому, используя гомоморфный анализ, можно определить период основного тона и частотные свойства голосового тракта. Общая схема гомоморфной обработки приведена на рис. 3.

 

Рис. 3. Общая схема гомоморфной обработки.

 В соответствии с этой схемой сначала выполняется нелинейное преобразование 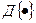 сигнала  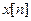, которое определяется отношением:

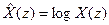 . (6)

Затем выполняется оператор  , который соответствует линейной инвариантной системе. В конце реализуется преобразование  .

Пусть сигнал 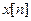  является сверткой двух последовательносте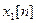й   и 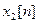  . Тогда:

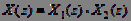 . (7)

Подставив (7) в (6), получим:

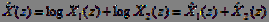 . (8)

Линейная инвариантная система пропускает на выход только одну из компонент 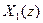  или 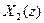  . Соответственно обратное преобразование  дает  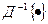 или 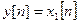  . Следовательно, гомоморфная обработка разделяет входные компоненты  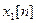 и 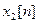  , содержащиеся во входном сигнале.

  

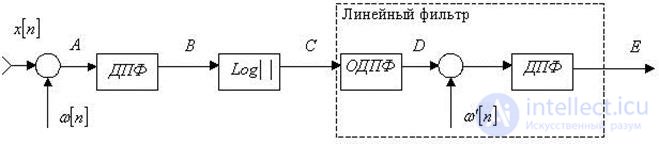
Рис. 4. Гомоморфная система анализа речи.

 Гомоморфная система анализа речи показана на рис. 4. Здесь на первом этапе вычисляется логарифм модуля кратковременного преобразования Фурье. Если предположить, что сигнал в точке А является сверткой функции возбуждения и импульсной характеристики голосового тракта, то в точке С мы получим сумму логарифмов спектра функции возбуждения и импульсной характеристики голосового тракта. Сигнал в точке D, полученный с помощью обратного дискретного преобразования Фурье, называется кепстром. Кепстр в точке D равен сумме кепстров функции возбуждения и импульсной характеристики голосового траста.

 

Кепстр  — энергетический спектр функции 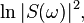  определяемый выражением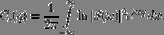 

 

Другими словами, кепстр определяет последовательность коэффициентов разложения функции lg [Ф (z)] в степенной ряд.

Аргумент q имеет размерность времени, но это особое, кепстральное время, поскольку  в любой момент q зависит от функции  исходного сигнала со спектром   заданной при 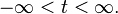  Иногда q называют «сачтота» или «кьюфренси» (анаграммы от рус. частота или англ. frequency).

В английском языке есть два аналога этого понятия — Kepstrum и Cepstrum.

 

 

1.         Кратковременное преобразование Фурье одномерного сигнала. Частотно-временной анализ сигналов.

 

В заключение, эта статья об анализ речевых сигналов в частотной области гомоморфная обработка речи подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое анализ речевых сигналов в частотной области гомоморфная обработка речи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Методы и средства компьютерных информационных технологий

Из статьи мы узнали кратко, но содержательно про анализ речевых сигналов в частотной области гомоморфная обработка речи