Лекция
Привет, Вы узнаете о том , что такое волновые процессы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое волновые процессы, элементы теории музыки, электромагнитные волны , настоятельно рекомендую прочитать все из категории Колебания и волны (Оптика, акустика и радиофизика).
В предыдущих главах изучались колебания в системах с одной, максимум с двумя степенями свободы. Теперь мы переходим к системам с бесконечным числом степеней свободы. Примерами могут служить колебания в газовой среде, колебания твердых тел, натянутой струны и т. п. Во всех этих примерах колебания возможны в каждой точке среды или тела, которую можно рассматривать как осциллятор. Соседние осцилляторы связаны между собой, так что между ними возможны процессы передачи энергии. В таких случаях говорят о распространяющейся волне.
Колебания струны
Рассмотрим малые колебания струны, натянутой силой Т вдоль оси х. Пусть смещение произвольной точки струны с координатой х в момент времени t есть вектор  . Ограничимся простейшим колебательным процессом, когда все векторы смещения
. Ограничимся простейшим колебательным процессом, когда все векторы смещения 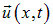 в любой момент времени перпендикулярны оси х и лежат в фиксированной плоскости. Тогда смещения точек струны можно описать одной скалярной функцией
в любой момент времени перпендикулярны оси х и лежат в фиксированной плоскости. Тогда смещения точек струны можно описать одной скалярной функцией 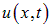 , как показано на рис. 2.1.
, как показано на рис. 2.1.

Рис. 2.1. Колебания струны
Напряжения, возникающие в струне, направлены по касательным к ее мгновенному профилю. Мы будем рассматривать малые колебания, когда можно пренебречь удлинением струны и возникающими при этом дополнительными силами упругости. Тогда натяжение струны можно считать постоянным для всех моментов времени t и точек х. Выделим элемент струны, лежащий между координатами х и  . Рассмотрим точку с координатой х. Тангенс угла наклона силы T, действующей на этот край элемента, равен
. Рассмотрим точку с координатой х. Тангенс угла наклона силы T, действующей на этот край элемента, равен

Вертикальная компонента силы равна
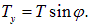
Так как угол 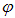 мал, то
мал, то

Тогда
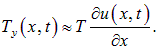
Аналогично, вертикальная компонента силы натяжения струны, действующей на другом конце выделенного элемента, равна
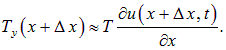
Равнодействующая этих сил равна
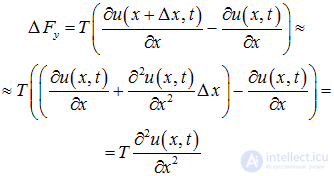
Заметим, что горизонтальные компоненты силы натяжения

не зависят от положения точки и потому их равнодействующая равна нулю. Это означает, что в рассматриваемом приближении элементы струны движутся только в вертикальном направлении.
Если линейная плотность (масса единицы длины) струны равна  , то масса элемента равна
, то масса элемента равна
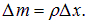
Записываем уравнение второго закона Ньютона для вертикального смещения элемента струны:

Подставляя сюда выражение для 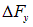 , получаем уравнение движения струны:
, получаем уравнение движения струны:
|
|
|
(2.1) |
Это уравнение можно переписать в виде:
|
|
|
(2.2) |
где
|
|
|
(2.3) |
Определим размерность величины  . Размерность силы
. Размерность силы

размерность линейной плотности материала струны
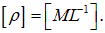
Отсюда размерность величины  будет
будет
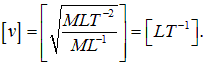
то есть величина  имеет размерность скорости.
имеет размерность скорости.
Колебания в идеальном газе
Рассмотрим колебания в газе, происходящие вдоль одной оси х. В отличие от струны частицы газа смещаются здесь в продольном направлении, но величины смещения мы будем обозначать тем же символом u(x,t).
Рассмотрим элементарный объем газа V0, ограниченный сечениями 1 и 2, находящимися в точке с координатами х и  (рис. 2.2). Масса газа в объеме равна
(рис. 2.2). Масса газа в объеме равна 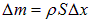 , где
, где 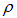 — плотность газа, a S — площадь поперечного сечения. В равновесном стационарном состоянии давление газа равно
— плотность газа, a S — площадь поперечного сечения. В равновесном стационарном состоянии давление газа равно 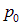 .
.
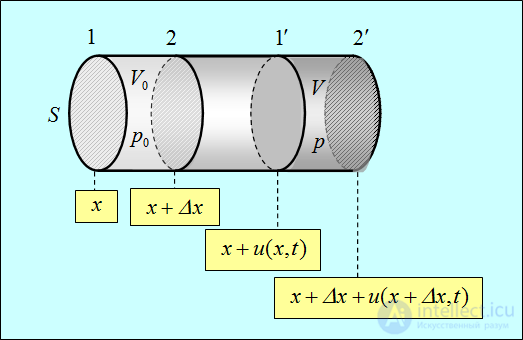
Рис. 2.2. Колебания в газе
При колебаниях выделенный объем смещается в новое положение между сечениями 1' и 2' с координатами

и

Объем газа в новом положении становится равным

а давление в нем — р. Найдем это давление.
Колебательные процессы в газах происходят достаточно быстро, так что можно считать, что элементарный объем не успевает обмениваться теплотой с соседними объемами. Значит, процесс можно считать адиабатным. Записываем уравнение этого процесса:

или

откуда
|
|
|
(2.4) |
Здесь  — показатель адиабаты, зависящий от вида газа. Мы использовали также малость производной
— показатель адиабаты, зависящий от вида газа. Мы использовали также малость производной

для разложения в ряд:

Составим теперь уравнение движения элементарного объема. Его ускорение равно

Сила, действующая на объем, определяется разностью давлений в сечениях 1' и 2':
|
|
|
(2.5) |
Подставляя сюда выражение для давления р находим:
|
|
|
(2.6) |
Записываем теперь уравнение второго закона Ньютона

или
|
|
|
(2.7) |
После очевидных сокращений это уравнение можно представить в виде:
|
|
|
(2.8) |
где
|
|
|
(2.9) |
Величина  имеет размерность скорости. Уравнение колебаний газа совпало с уравнением колебаний струны (2.2), хотя они описывают процессы в совершенно различных физических системах.
имеет размерность скорости. Уравнение колебаний газа совпало с уравнением колебаний струны (2.2), хотя они описывают процессы в совершенно различных физических системах.
Колебания в твердых телах
Колебательные процессы в твердых телах похожи на колебания в газах. На рис. 2.3 представлена продольная деформация твердого тела в направлении оси х.
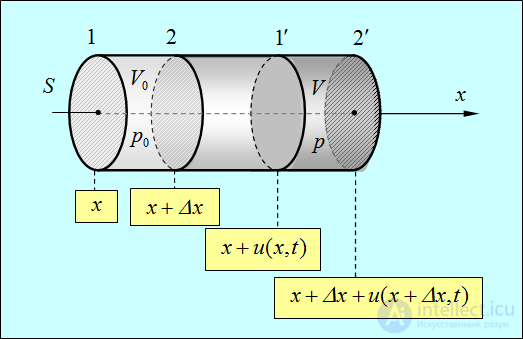
Рис. 2.3. Продольные колебания в твердом теле
Относительная деформация элементарного объема при смещении u равна

Согласно закону Гука, это приводит к появлению упругой силы
|
|
|
(2.10) |
где Е — коэффициент (модуль Юнга), характеризующий жесткость среды. Равнодействующая сил упругости, действующих в сечениях 1' и 2' равна:
|
|
|
(2.11) |
Записывая второй закон Ньютона в виде:
|
|
|
(2.12) |
находим уравнение колебаний в твердом теле:
|
|
|
(2.13) |
где
|
|
|
(2.14) |
Размерность модуля Юнга совпадает с размерностью давления, так что  и здесь имеет размерность скорости.
и здесь имеет размерность скорости.
Выше мы рассматривали продольные смещения в твердом теле. В отличие от газов, упругие силы возникают в твердых телах и при деформации сдвига. Уравнение для таких поперечных колебаний имеет тот же вид (2.13), но вместо модуля Юнга в выражении для v будет стоять так называемый модуль сдвига G:
|
|
|
(2.15) |
Механизм распространения продольных и поперечных колебаний показан на рис. 2.4 и 2.5.

Рис. 2.4. Продольные волны в твердом теле

Рис. 2.5. Поперечные волны в твердом теле
Уравнение типа (2.2), описывающее колебания различных упругих сред, называется волновым уравнением. Запишем его формально в виде:
|
|
|
(2.16) |
или
|
|
|
(2.16') |
Введем теперь вместо (x, t) новые переменные:
|
|
|
(2.17) |
Производные по новым переменным выражаются по стандартным правилам дифференцирования сложной функции:

Отсюда следует, что уравнение (2.16) в новых переменных записывается в виде:
|
|
|
(2.18) |
Поскольку производная по  равна нулю,
равна нулю,
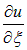
не зависит от этой переменной и, следовательно, является некоторой функцией w только от переменной  :
:
|
|
|
(2.19) |
Интегрируем теперь это уравнение:
|
|
|
(2.20) |
Первое слагаемое в правой части является только функцией переменной  , которую мы обозначим как
, которую мы обозначим как  . Второе слагаемое — постоянная интегрирования. Она не зависит от
. Второе слагаемое — постоянная интегрирования. Она не зависит от  , являясь, стало быть, функцией только переменной
, являясь, стало быть, функцией только переменной  :
:

Мы получили, что решение волнового уравнения имеет вид:

Подставляя сюда выражения (2.17), мы возвращаемся к прежним переменным (x, t):
|
|
|
(2.21) |
Функции f1 и f2 — совершенно произвольны и должны быть определены из начальных и граничных условий.
Обсудим физический смысл полученных решений. Ограничимся сначала первым слагаемым. Пусть

В момент времени t = 0 функция f1(x) задает распределение смещений (профиль струны, деформацию твердого тела, распределение давления или частиц в газе и т. д.):

Предположим, например, что это распределение имеет максимум в точке  (рис. 2.6).
(рис. 2.6).
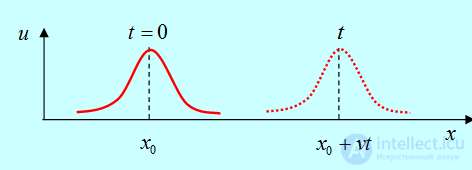
Рис. 2.6. Движение волнового пакета f1(x – vt)
Такое распределение называют обычно волновым пакетом. В момент t максимум функции  по-прежнему будет в точке, в которой аргумент
по-прежнему будет в точке, в которой аргумент  равен
равен  , но теперь (в момент времени
, но теперь (в момент времени  ) аргумент равен
) аргумент равен  , таким образом:
, таким образом:  или
или  . Другими словами, за время от 0 до
. Другими словами, за время от 0 до  волновой пакет сдвинется вправо на расстояние vt, так что максимум теперь придется на точку
волновой пакет сдвинется вправо на расстояние vt, так что максимум теперь придется на точку

Нетрудно сообразить, что форму свою волновой пакет при этом перемещении не изменит.
Мы видим, что начальное распределение движется вправо со скоростью 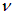 . Аналогично, второе слагаемое,
. Аналогично, второе слагаемое,  , описывает движение волнового пакета налево с той же скоростью
, описывает движение волнового пакета налево с той же скоростью 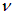 . Общее решение (2.21) является суперпозицией двух этих решений.
. Общее решение (2.21) является суперпозицией двух этих решений.
В свою очередь, любой волновой пакет может быть представлен как суперпозиция гармонических функций. Отсюда — особая роль решений волнового уравнения вида:
|
|
|
(2.22) |
Это решение описывает монохроматическую волну, распространяющуюся направо со скоростью
|
|
|
(2.23) |
Действительно, выражение (2.22) можно представить в виде

что является одной из бесчисленных возможностей конкретного воплощения функции f(x–vt) в (2.21). Величина  – это циклическая частота колебаний, а k называется волновым числом.
– это циклическая частота колебаний, а k называется волновым числом.
Пусть наблюдатель находится в точке  и следит за колебаниями среды в этой точке. Он обнаружит, что колебательное движение происходит по закону
и следит за колебаниями среды в этой точке. Он обнаружит, что колебательное движение происходит по закону
|
|
|
(2.24) |
Наблюдатель в другой точке также обнаружит гармонические колебания с той же частотой, но с другой начальной фазой  . Чем правее точка наблюдения, тем большее запаздывание по фазе имеют там колебания. Соответственно, выражение
. Чем правее точка наблюдения, тем большее запаздывание по фазе имеют там колебания. Соответственно, выражение

описывает монохроматическую волну, распространяющуюся налево.
Проведем теперь другой мысленный опыт: «сфотографируем» нашу волну в какой-то данный момент времени  (в случае колеблющейся струны для этого даже не нужно изощренных приборов). На снимке мы увидим периодическую пространственную структуру:
(в случае колеблющейся струны для этого даже не нужно изощренных приборов). На снимке мы увидим периодическую пространственную структуру:
|
|
|
продолжение следует...
Часть 1 2. Волновые процессы и Элементы теории музыки
Часть 2 2.3. Энергия волны - 2. Волновые процессы и Элементы теории
Часть 3 2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -
Часть 4 2.5. Сферические волны - 2. Волновые процессы и Элементы теории
Часть 5 - 2. Волновые процессы и Элементы теории музыки
Часть 6 - 2. Волновые процессы и Элементы теории музыки
Часть 7 - 2. Волновые процессы и Элементы теории музыки
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика