2.5. Сферические волны - 2. Волновые процессы и Элементы теории

Это продолжение увлекательной статьи про волновые процессы.

...

того или иного гласного звука, как не имеет его простая гитарная струна: музыкальные инструменты говорить не умеют. Исходный тембр голосовой щели приобретает характер речевого звука при прохождении по рото-глоточному каналу. Со времен исследований Гельмгольца по акустике известно, что каждый гласный звук содержит в своем спектре две основные, относительно усиленные области частот — форманты гласных, или характеристические тоны Гельмгольца. По ним наше ухо отличает один гласный звук от другого. Одна из частот связана с резонансом глотки, вторая — с резонансом ротовой полости. Ротовая полость меньше по объему, и потому объем воздуха в ней резонирует на более высокие частоты — порядка килогерц, глоточная полость по размеру больше, и резонирует она на частоты порядка нескольких сот герц. (Зависимость резонансной частоты от размера полости резонатора такая же, как для частот на струне — чем короче струна, тем выше извлекаемая на ней частота.) Изменение относительных размеров этих полостей производится артикуляцией языка, перемещение которого создает в ротовой и глоточной полостях нужные для образования формант объемы воздуха. В старые времена преступникам вырезали язык, и они лишались возможности произносить гласные звуки, лишались дара речи, хотя голос у них и сохранялся. Форманты для гласных русского языка имеют примерно следующие значения: и – 240 Гц и 2 250 Гц, у – 300 Гц и 650 Гц, е – 440 Гц и 1 800 Гц, о – 535 Гц и 780 Гц, а – 700 Гц и 1 000 Гц. У женщин и детей формантные области несколько смещены в сторону более высоких частот, и благодаря этому мы различаем, кто говорит с нами, даже если частота основного звука будет одной и той же. Важно, что формантные области остаются постоянными, несмотря на изменение высоты основного тона: человек может произнести гласную е басом или тенорком, но формантные частоты будут теми же самыми (рис. 2.15). Некоторые отличия в числах между приведенными данными и рисунком связаны с тем, что измерения слегка отличаются у разных групп исследователей.

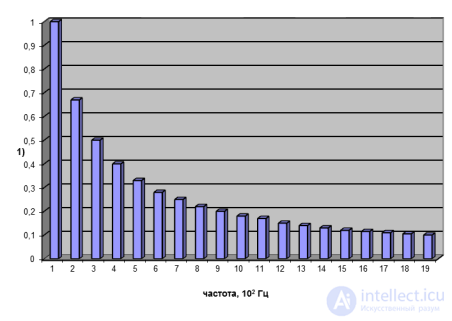
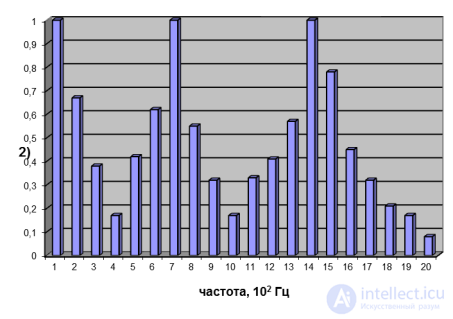
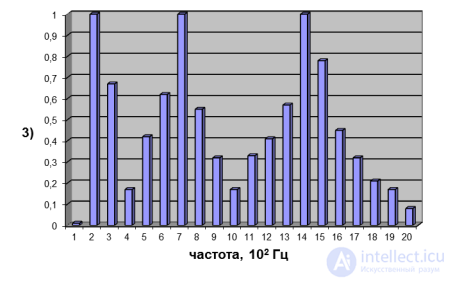
Рис. 2.15. Спектр гортани, состоящий из равномерно убывающих по амплитуде обертонов (1) и спектры звука е,
взятого на частоте 100 Гц (2) и 200 Гц (3). Формантные области n = 700 Гц и n = 1 400 Гц
остаются неизменными, несмотря на изменение высоты основного тона

При изучении не речи, но уже пения, были открыты еще две области обертонов — так называемые певческие форманты. В 20–30-е гг. было обнаружено, что в спектре хорошо поставленного мужского голоса всегда присутствуют усиленные обертоны с частотой в области 500 Гц. Наличие этой низкой певческой форманты придает голосу округлое, полное и мягкое звучание. Высокая певческая форманта лежит в области 3 000 Гц, она привносит в звук яркость, блеск, создает серебристость тембра. У мастеров вокального искусства в области высокой певческой форманты сосредоточено до 30–35 % всей звуковой энергии голоса, в речи же, даже поставленной (у дикторов и актеров) — только 5–7 %. Чем интенсивнее звук, тем более выражены певческие форманты по сравнению с формантами гласных. Поэтому при большой мощности звука гласные становятся плохо различимыми, и мы узнаем их скорее по контексту, в начальный момент формирования звука. На рис. 2.16 показан спектр голоса Ф. Шаляпина.

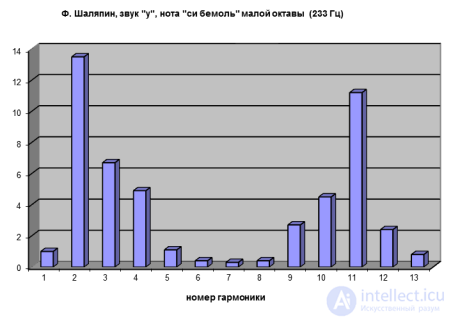
Рис. 2.16. Спектр голоса Ф. Шаляпина. Основной тон у Шаляпина в общем спектре роли не играет.
Его амплитуда принята на рисунке за единицу. Основная энергия заключена в низкой певческой форманте — 2–4 обертонах.

Высокая певческая форманта возникает в гортани человека — в надсвязочной полости между голосовыми связками и входом в гортань. Эта полость имеет размеры порядка 3 см, что при скорости звука v = 340 м/с приводит к резонансу на частоте

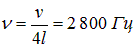
(основной тон закрытой трубы, который мы обсуждали выше), то есть как раз в области высокой певческой форманты. Место возникновения низкой певческой форманты точно не определено: данные указывают, скорее всего на резонанс трахеальной трубки.

С тембром голоса, в присутствии в его спектре высоких обертонов, связано качество «полетности». Существуют певческие голоса, летящие в зал и «пробивающие» звучание оркестра, причем иногда они не имеют большой силы. И наоборот, есть голоса необыкновенной мощи, теряющиеся в больших помещениях, заглушаемые звучанием оркестра. Качество полетности оказалось связанным с особенностями нашего слуха, который наиболее восприимчив к области частот 2 500 – 3 000 Гц. На эти частоты резонирует наружный слуховой проход уха, и такие звуки субъективно воспринимаются как более громкие. Как мы уже знаем, это — область высокой певческой форманты. Голоса, в которых большой процент энергии концентрируется в высокой певческой форманте, обладают способностью «лететь через оркестр», они хорошо слышны в большом зале.

2. Высота звука и устройство музыкальной шкалы

Равномерная темперация

Одной из важнейших характеристик музыкального звука является его высота, количественной мерой которой служит частота n колебаний соответствующего вибратора (столбика воздуха в духовых инструментах, струны — в струнных и т. п.). Частота колебаний может принимать любые значения, но с точки зрения восприятия музыкального звука наблюдается известная периодичность: два звука воспринимаются как аналогичные, если частота одного из них ровно в два раза превышает частоту другого. Эту аксиому эквивалентности звуков провозгласил в 1722 г. французский композитор Жан Филипп Рамо. Таким двум звукам соответствует одна и та же нота, и, как говорят, их разделяет интервал, называемый октавой.

Международным стандартом для ноты «ля» первой октавы установлена частота 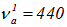Гц. Нота «ля» следующей, второй октавы, имеет частоту, ровно в два раза большую — 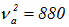Гц. В европейской системе октава делится на двенадцать разных звуков (вспомните, например, семь белых и пять черных клавиш в каждой октаве фортепиано). Интервал между соседними звуками называется полутоном. Как же настроить соответствующие вибраторы, исходя из стандартной частоты 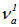? Один из способов — равномерный строй (как говорят музыканты – равномерная темперация), когда отношение между частотами соседних звуков постоянно. Это отношение, как легко понять, равно

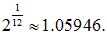
Именно это число, будучи умноженным само на себя 12 раз, дает в результате удвоение частоты для той же ноты в следующей октаве:

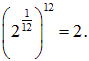
Приняв равномерно-темперированный строй, мы можем рассчитать частоты любых нот. Так, нота «ля» первой октавы и нота «до» второй октавы разделены тремя полутонами, то есть частота последней должна равняться

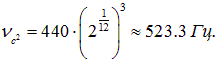
Соответственно, частота 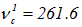Гц ноты «до» первой октавы получается отсюда делением на двойку. Нота «соль» первой октавы отстоит от «до» той же октавы на семь полутонов, то есть ее частота равна

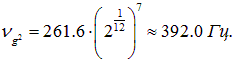
Результаты подобных расчетов для четырех октав приведены в таблице 2.2.

Таблица 2.2.

Высота музыкальных звуков при равномерно-темперированном строе: для каждой ноты указаны ее международное (латинское) обозначение и частота в герцах

Заметим, кстати, что эти октавы выбраны для примера не случайно: именно в этом диапазоне лежит голос человека. Самый высокий женский певческий голос — сопрано, для которого характерен диапазон с¹–e³ (редко — до g³). На несколько тонов ниже лежит диапазон меццо-сопрано: а–h². Самый низкий женский голос — контральто, его типичный диапазон — f–а². Особо надо упомянуть контратеноров — современных исполнителей произведений, написанных некогда для певцов-кастратов. Но диапазон последних был необычайно широк, и немногие из нынешних певцов в полной мере могут воспроизвести некогда популярные произведения. «Типичные» контратеноры (если можно говорить о типичности столь редких голосов) поют в диапазоне (c–e²), отличаясь от контральто тембром.

Самый высокий из обычных мужских голосов — тенор, для него типичен диапазон с–с². Далее следуют баритон (А–f¹) и бас (С–е¹). Таким образом, «вокальные» частоты простираются от примерно 70 Гц до 1 400 Гц (здесь идет речь об основной ноте, а не о примеси обертонов). Примерные диапазоны певческих голосов показаны на рис. 2.17 вместе с диапазонами струнных инструментов — скрипки, альта, виолончели и контрабаса. Король инструментов — концертный рояль — содержит обычно 7.25 октав: от А₂ (27.5 Гц) до с⁵ (4 186 Гц).

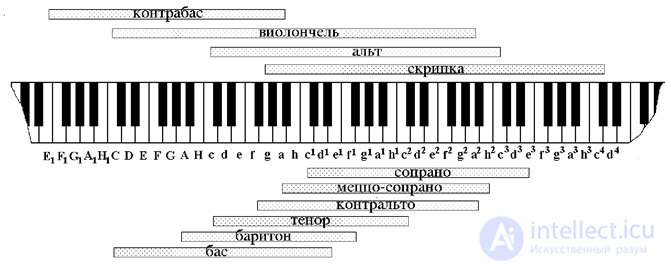
Рис. 2.17. Примерные диапазоны струнных инструментов и человеческих голосов

Идея равномерной темперации родилась в Германии на рубеже XVII–XVIII веков. Приведенная музыкальная шкала поначалу встретила сопротивление, но после сочинения И.С. Бахом в 1722–1744 гг. «Хорошо темперированного клавира» — сборника прелюдий и фуг, по одной на каждую из существующих 24 тональностей, – жизнеспособность новой шкалы была доказана. С тех пор она и стала общепринятой. Основное достоинство равномерно темперированной шкалы — это возможность транспонировать мелодию в другой диапазон без ее искажения. Например, мелодия «Чижика» (ми¹ – до¹ – ми¹ – до¹ – фа¹ – ми¹ – ре¹), играемая в первой октаве, соответствует последовательности частот (в Гц): 330–262–330–262–349–330–294 (мы округлили значения, приведенные в таблице 3.2). Предположим, мы хотим сыграть ее, перенеся начало на три клавиши выше — с ноты «си», которой соответствует частота 494 Гц. Отношение первых нот оригинальной и транспонированной мелодий равно 493.7/329.6=1.4983=2^7/12 (показатель степени соответствует семи полутонам, разделяющий ноты «ми» и «си» — см. рис. 3.17). Таким же должно быть отношение вторых и всех последующих нот мелодии. Стало быть, последовательность частот транспонированной мелодии должна иметь вид 494–392–494–392–523–494–440, то есть транспонированная мелодия прозвучит как си¹ – соль¹ – си¹ – соль¹ – до² – си¹ – ля¹.

Почему же равномерно темперированная музыкальная шкала вызывала возражения? Дело в том, что еще в древности, со времен Пифагора, было известно, что некоторые ноты, взятые одновременно, звучат в консонанс, благозвучно, не вступают в противоречие друг с другом. К таким двузвучиям Пифагор относил октаву (отношение частот 2:1), квинту (3:2) и кварту (4:3)— так называемые совершенные консонансы. Позже к ним причислили еще большую и малую терции (5:4 и 6:5). Что же общего между консонансом двузвучия и отношением первых шести целых чисел?

Разберемся, что происходит, когда одновременно берутся две ноты. Нижний по высоте звук называется основанием интервала, верхний — его вершиной. Пусть основанию соответствует частота v₁ при звучании струны на этой ноте неизбежно будут возбуждаться и первые обертоны с частотами v₂ = 2v₁, v₃ = 3v₁, v₄ = 4v₁. Если теперь одновременно с первой нотой взять другую, образующую с первой интервал в октаву (соответствующая ей частота равна v₂ = 2v₁), то на ней тоже будут возникать обертоны с частотами v₄=2v₂ = 4v₁, v₆ = 3v₂ = 6v₁ и т. д. Мы видим, что состав созвучия, в сущности, не изменился — добавление новой ноты не прибавило новых обертонов. Поэтому октава и звучит почти как одна нота, абсолютный консонанс.

«Примесь» второй гармоники всегда существует при колебании любого вибратора, и, может, это и есть причина того, что наше ухо воспринимает одинаковые ноты в разных октавах как звучащие в унисон, как, в сущности, ту же самую ноту. В этом, видимо, заключена физическая основа аксиомы эквивалентности Рамо, само понятие октавы как некой меры периодичности музыкального звука, когда начинают повторяться те же самые ноты.

Попутно мы установили, что нота, соответствующая частоте v₃ = 3v₁ тесно связана с первоначально взятой нотой — так или иначе, но этот звук уже присутствует в изначальном как его третья гармоника. Но по теореме эквивалентности этой ноте в предыдущей октаве соответствует частота v_1quint=3v₁/2. Таким образом, интервал, где основанию соответствует частота v₁, а вершине — частота v_quint = 3n₁/2, будет благозвучным. Такой интервал называется, напомним, квинтой, и отношение частот вершины и основания в квинте в точности равно 3/2.

Возьмем теперь благозвучную квинту — двузвучие с частотами v₁ и v_quint = 3v₁/2, — и добавим к нему третью ноту, составляющую октаву с основанием. Ее частота равна 2v₁. По теореме эквивалентности, благозвучие этого созвучия не нарушится. Но если благозвучен интервал между основанием и третьей нотой (октава) и благозвучен интервал между основанием и вершиной двузвучия (квинта), то должен быть благозвучен и интервал между вершиной и третьей нотой. Соответствующее отношение частот равно v₂/v_quint = 2v₁/(3v₁/2) = 4:3. Такой интервал называется, как мы помним, квартой. Если за основание интервала взять все ту же ноту с частотой v₁, то кварту с ней образует нота, звучащая на частоте v_quart = 4v₁/3.

В принципе, эти отношения целых чисел можно было бы положить в основу построения музыкальной шкалы. Но тогда возникнет проблема с транспонированием мелодии.

Попробуем построить одну октаву гипотетической музыкальной шкалы, а) основанной на отношении целых чисел и б) допускающей транспонирование мелодии. Пусть эта шкала содержит какую-то ноту с частотой v. Тогда в ней должна содержаться также и нота, образующая с исходной интервал в октаву (2v). Пусть также в шкале имеется еще одна нота, образующая с первой, например, чистую квинту (3v/2). Тогда шкала должна содержать и ноту, отстоящую от первой на две квинты: ее частота равна (3/2)²v = 9v/4, а понижение на октаву дает нам ноту 9v/8. Понижение на октаву комбинации трех квинт приводит к ноте с частотой v/(3/2)³/2 = 27v/16, понижение на две октавы комбинации четырех квинт приводит к частоте 81v/64 и т. д. Продолжая этот процесс, мы получим бесконечное число нот в пределах одной октавы, ибо никакая степень тройки не станет равной какой-то степени двойки (нечетное число не может быть равным четному). Значит, описанная процедура будет приводить все к новым и новым нотам, которые необходимо включить в шкалу. Тот же результат получается, если строить шкалу на основе кварт, а не квинт. Таким образом, требования а) и б) к музыкальной шкале оказываются несовместимыми. Надо отказаться от одного из них, и проще пожертвовать отношением целых чисел для совершенных консонансов, приобретая свободу выбора тональностей и легкость транспонирования мелодий.

Поэтому музыканты отказались от настройки своих инструментов по закону отношения целых чисел, и перешли к равномерной темперации. При этом частоты совершенных консонансов воспроизводятся приблизительно. Например, в равномерно темперированной шкале квинте соответствует интервал в 7 полутонов: 2^7/12 = 1.4983, что лишь на 0.1 % отличается от чистой квинты (отношения 1.5). Таков интервал, например, между нотами «до» и «соль». Кварте соответствует интервал в 5 полутонов: 2^5/12 = 1.3348, что отличается от чистой кварты (1.3333) также на 0.1 % (опытному уху слышны даже столь малые отличия от идеальных интервалов).

Было бы интересно обсудить физические принципы, лежащие в основе мажорного (до–ми–соль) и минорного (до–ми бемоль–соль) трезвучий, но это увело бы нас слишком далеко от физики, к которой пора возвращаться. Мы надеемся, однако, что музыкальные примеры помогли усвоить важные понятия высших гармоник и спектра колебаний, с которыми нам еще предстоит встретиться.

2.5. Сферические волны

В предыдущих разделах мы рассматривали специальный тип волн: фаза

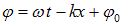
зависела только от координаты х.

Для изученных нами волн колебания среды одинаковы во всех точках плоскости, ортогональной направлению распространения волны (мы выбрали его в качестве оси х). Иными словами, фронт волны является плоскостью, параллельной плоскости, содержащей оси у, z. Фронт бегущей волны перемещается с течением времени вдоль оси х с фазовой скоростью v. Такие волны называются плоскими.

Трехмерное волновое уравнение

Пусть мы по-прежнему имеем дело с плоской волной. Повернем координатные оси так, чтобы направление распространения волны задавалось каким-то единичным вектором n. Решение, очевидно, имеет вид:

Соотношения между 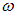, k и 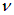остаются прежними.

Фронт волны – плоскость, ортогональная волновому вектору k, – движется со скоростью v, оставаясь параллельным самому себе.

Найдем уравнение, которому удовлетворяет решение (2.65). Дважды дифференцируем выражение (2.65) по координатам х, у, z:

Складывая эти три уравнения, находим:

Вторая производная решения по времени имеет вид:

Учитывая соотношение

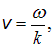
получаем из (2.67), (2.68):

продолжение следует...

Продолжение:

Часть 1 2. Волновые процессы и Элементы теории музыки
Часть 2 2.3. Энергия волны - 2. Волновые процессы и Элементы теории
Часть 3 2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -
Часть 4 2.5. Сферические волны - 2. Волновые процессы и Элементы теории
Часть 5 - 2. Волновые процессы и Элементы теории музыки
Часть 6 - 2. Волновые процессы и Элементы теории музыки
Часть 7 - 2. Волновые процессы и Элементы теории музыки