- 2. Волновые процессы и Элементы теории музыки

Это продолжение увлекательной статьи про волновые процессы.

...

loading="lazy" alt="2. Волновые процессы и Элементы теории музыки" >

(2.89)

Используя соотношение

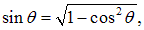
получаем связь скорости самолета с высотой полета и временем t:

откуда:

Подставляем числовые данные:

Число Маха (здесь ) равно

При такой скорости движения самолет удалился по горизонтали на расстояние

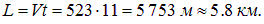
Заметим, кстати, что момент прихода к наблюдателю фронта ударной волны воспринимается как резкий хлопок (подобный грому). Бытующее выражение «самолет преодолел звуковой барьер» неверно отражает физический процесс: хлопок, как мы видели, не связан с моментом, когда самолет приобрел сверхзвуковую скорость.

На рис. 2.25 демонстрируется прохождение ударной волны при движении сверхзвукового самолета.

Рис. 2.25. Прохождение ударной волны при движении сверхзвукового самолета

Проанализируем формулу (2.90). Видно, что время задержки t не может быть больше, чем

Такая задержка могла бы быть при очень большой скорости самолета (V>>v), когда конус Маха становится крайне узким, почти параллельным направлению движения. Фронту ударной волны, распространяющемуся вертикально вниз, надо при этом пройти расстояние h, что он и осуществляет за время .

Время задержки t = 0 соответствует случаю, когда скорость самолета равна скорости звука: V = v. При этом угол раствора конуса Маха становится равным (рис. 2.26), так что ударная волна доходит до наблюдателя в тот самый момент, когда самолет оказывается у него над головой.

Рис. 2.26. Фронт ударной волны в случае движения источника со скоростью звука. В каждый момент времени t источник находится на поверхности всех сферических волн, испущенных ранее. Огибающая этих сферических волн – фронт ударной волны – представляет собой плоскость, ортогональную направлению движения источника

При дозвуковых скоростях звук опережает летательный аппарат и приходит к наблюдателю раньше самолета.

2.6. электромагнитные волны

Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды () и токи (j = 0):

где

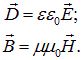
Величины и — электрическая и магнитная постоянные, соответственно, которые связаны со скоростью света в вакууме соотношением

Постоянные и характеризуют электрические и магнитные свойства среды, которую мы будем считать однородной и изотропной.

В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.

Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.

При строго гармоническом изменении во времени векторов и электромагнитная волна называется монохроматической.

Получим из уравнений Максвелла волновые уравнения для векторов и .

Волновое уравнение для электромагнитных волн

Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.

Возьмем ротор от обеих частей уравнения

При этом воспользуемся доказываемой в курсе математики формулой:

где — введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:

Получаем в итоге:

Выразим rotB через электрическое поле с помощью уравнения Максвелла:

и используем это выражение в правой части (2.93). В результате приходим к уравнению:

Учитывая связь

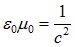
и вводя показатель преломления среды

запишем уравнение для вектора напряженности электрического поля в виде:

Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:

Взяв ротор от обеих частей уравнения Максвелла

и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:

Полученные волновые уравнения для и 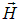означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна

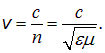
В отсутствие среды (при ) скорость электромагнитных волн совпадает со скоростью света в вакууме.

Основные свойства электромагнитных волн

Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:

Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:

Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:

Дифференцирование плоских волн по времени дает:

Тогда из уравнений Максвелла следует:

Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:

Далее, ни у , ни у нет компонент параллельных оси х:

Иными словами и в изотропной среде,

Тогда можно выбрать координатные оси так, чтобы вектор был направлен вдоль оси у (рис. 2.27):

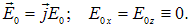
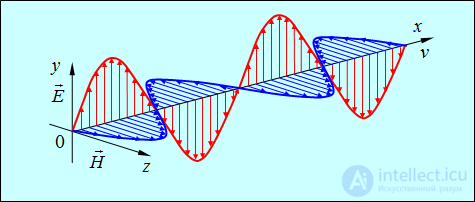
Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне

В этом случае уравнения (2.103) приобретают вид:

Отсюда следует, что вектор направлен вдоль оси z:

Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:

Отсюда вытекает обычная связь волнового вектора, частоты и скорости:

а также связь амплитуд колебаний полей:

Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.

Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.

Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).

На рис. 2.28 представлена шкала электромагнитных волн.

Рис. 2.28. Шкала электромагнитных волн

Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.

Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.

Эффект Доплера для электромагнитных волн

Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:

Наблюдатель в другой инерциальной системе отсчета К', движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t', r'. Связь между системами отсчета дается преобразованиями Лоренца:

Подставим эти выражения в выражение для фазы , чтобы получить фазу волны в движущейся системе отсчета:

Это выражение можно записать как

где и — циклическая частота и волновой вектор относительно движущейся системы отсчета. Сравнивая с (2.110), находим преобразования Лоренца для частоты и волнового вектора:

Для электромагнитной волны в вакууме

Пусть направление распространения волны составляет в первой системе отсчета угол 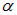с осью х:

Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:

Это и есть формула Доплера для электромагнитных волн.

Если , то наблюдатель удаляется от источника излучения и воспринимаемая им частота волны уменьшается:

Если , то наблюдатель приближается к источнику и частота излучения для него увеличивается:

При скоростях V << с можно пренебречь отклонением квадратного корня в знаменателях от единицы, и мы приходим к формулам, аналогичным формулам (2.85) для эффекта Доплера в звуковой волне.

Отметим существенную особенность эффекта Доплера для электромагнитной волны. Скорость движущейся системы отсчета играет здесь роль относительной скорости наблюдателя и источника. Полученные формулы автоматически удовлетворяют принципу относительности Эйнштейна, и с помощью экспериментов невозможно установить, что именно движется — источник или наблюдатель. Это связано с тем, что для электромагнитных волн отсутствует среда (эфир), которая играла бы ту же роль, что и воздух для звуковой волны.

Заметим также, что для электромагнитных волн имеет место поперечный эффект Доплера. При частота излучения изменяется:

в то время как для звуковых

продолжение следует...

Продолжение:

Часть 1 2. Волновые процессы и Элементы теории музыки
Часть 2 2.3. Энергия волны - 2. Волновые процессы и Элементы теории
Часть 3 2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -
Часть 4 2.5. Сферические волны - 2. Волновые процессы и Элементы теории
Часть 5 - 2. Волновые процессы и Элементы теории музыки
Часть 6 - 2. Волновые процессы и Элементы теории музыки
Часть 7 - 2. Волновые процессы и Элементы теории музыки