2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -

Это продолжение увлекательной статьи про волновые процессы.

...

листьев

10

Шепот, тиканье часов

20

Уличный шум (без автотранспорта)

30

Нормальный разговор

60

Крик

80

Рок-группа

110

Болевой предел

120

Реактивный двигатель на расстоянии 50 м

130

Стартующая ракета на расстоянии 50 м

200

2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны

Помимо бегущих волн предыдущего раздела, в природе существуют и стоячие волны, образующиеся в результате суперпозиции бегущих. Мы постоянно встречаемся с ними в своей практической жизни: когда говорим, поем, слушаем музыку. В этом разделе, после общих математических формул, мы совсем коротко обсуждаем некоторые вопросы музыкальной акустики – в надежде, что эта часть не покажется нашим студентам самой скучной.

Струна, закрепленная на одном конце

Предположим, что струна закреплена неподвижно в точке с координатой 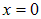и тянется в положительном направлении оси х. Пусть по струне справа налево (то есть в отрицательном направлении оси х) распространяется волна

Дойдя до точки закрепления, волна отразится. Если пренебречь потерями энергии, то амплитуда отраженной волны совпадет с амплитудой падающей волны. Надо учесть также, что при отражении происходит изменение направления движения элемента на обратное (как в упругом ударе шарика о стенку):

Суперпозиция падающей и отраженной волн имеет вид:

Мы видим, что в любой момент времени

Это и есть условие закрепления струны в точке 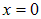. Воспользовавшись известными формулами тригонометрии для преобразования разности косинусов, записываем (2.53) в виде:

где 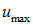— наибольшее смещение в стоячей волне.

Мы нашли особый тип колебаний: в каждой точке пространства струна колеблется с частотой 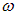и амплитудой 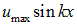, причем все точки струны одновременно достигают своих максимальных отклонений (или проходят положение равновесия), и если мы находимся, например, в узле струны, то есть в точке с координатой

то в любой момент времени эта точка остается узлом. Иными словами, здесь нет движения волны, точки узлов волны (нулевых значений смещения) неподвижны, равно как и точки ее максимумов. Такие колебания и называются стоячими волнами.

Это очевидно хотя бы потому, что точки узлов волны неподвижны, и переноса энергии через них быть не может. Можно рассуждать и иначе: две бегущие волны, образовавшие стоячую, переносят одну и ту же энергию, но в противоположных направлениях, так что оба эти процесса взаимно компенсируются.

На рис. 2.9 показано образование стоячей волны при сложении двух бегущих навстречу друг другу монохроматических волн.

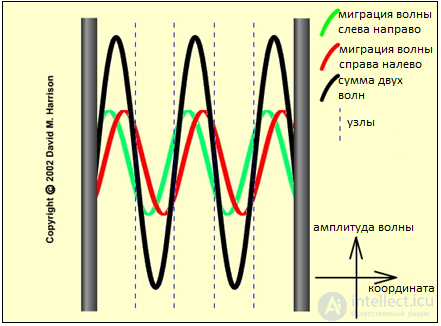
Рис. 2.9. Возникновение стоячей волны

Подставляя найденное решение (2.53) в выражение (2.39), получаем для мгновенного значения плотности энергии стоячей волны выражение

Усредняя по времени, находим:

Мы получили, что средняя плотность энергии стоячей волны не зависит от точки наблюдения и равна сумме средних плотностей энергий двух бегущих волн, суперпозицией которых она является.

Пример 1. Для струны, закрепленной на одном конце, найдем точки, в которых плотность энергии колебаний не зависит от времени.

Используя соотношение

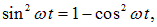
представим (2.54) в виде:

Теперь ясно, что зависимости от времени не будет, если

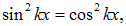
или

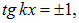
то есть в точках

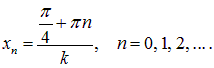
Пример 2. Найдем закон изменения во времени плотности энергии стоячей волны в точках, где смещение струны достигает своих максимальных значений.

Указанные точки имеют координаты

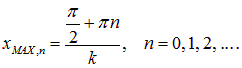
В этих точках

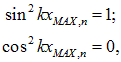
так что из (2.54) следует:

Гармоники

На струне, закрепленной на одном конце, могут существовать колебания любых частот. Закрепим теперь второй конец струны в точке с координатой 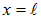. Имеем то же решение (2.53), которое должно удовлетворять дополнительному граничному условию:

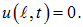
Это означает, что

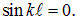
На струне длиной l, закрепленной на обоих концах, могут существовать только стоячие волны с волновыми векторами

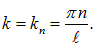
Соответственно, длины волн будут

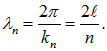
Иными словами, на длине струны должно укладываться целое число полуволн. Следовательно, закрепленная с обоих концов струна может колебаться только с определенными частотами:

Мы использовали здесь уравнение (2.2) для скорости волн на натянутой струне.

Из (2.58) видно, что частота колебаний повышается при:

• уменьшении длины струны;
• уменьшении ее толщины (линейной плотности);
• увеличении натяжения.

Эти закономерности известны каждому, кто держал в руках хотя бы гитару. Колебания с низшей частотой (n = 1) называются основной (первой) гармоникой, с последующими частотами — высшими (второй, третьей и т. п.) гармониками.

Аналогичные граничные условия существуют и для колебаний воздуха в трубах духовых музыкальных инструментов. Соответственно, в их сигналах также присутствуют только вполне определенные частоты. Рассмотрим, например, органную трубу длиной l. Волна давления в ней также может быть описана уравнением вида (2.53):

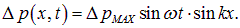
Если труба открыта с обеих сторон, то давление на концах равно стационарному (атмосферному) и 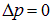в точках х = 0, l. Отсюда получаем те же условия для волновых чисел

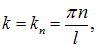
длин волн

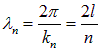
и частот

Если же труба открыта в точке х = 0 и закрыта на другом конце (х = l), то на закрытом конце смещение частиц равно нулю, а давление достигает максимума или минимума:

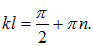
Отсюда следуют несколько иные соотношения:

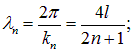
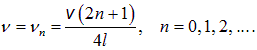
Первая гармоника для такой трубы возбуждается на частоте

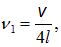
что в два раза меньше частоты

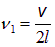
первой гармоники полностью открытой трубы.

Пример 3. Нейлоновая гитарная струна имеет линейную плотность массы 7.2 г/м и натянута с силой 150 Н. Длина струны 90 см. Определим, каковы четыре низшие частоты, извлекаемые на такой струне?

Скорость волны на струне равна

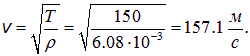
Наибольшая длина стоячей волны в струне равна 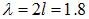м. Отсюда находим самую низкую частоту:

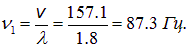
(Эта частота соответствует ноте «фа» большой октавы.)

Следующие частоты являются целыми кратными n₁:

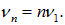
Отсюда следует: n₁ = 2·87.3 = 174.6 Гц («фа» малой октавы), n₃ = 3·87.3 = 261.9 Гц («до» первой октавы) и n₁ = 4·87.3 = 349.2 Гц («фа» первой октавы).

Пример 4. Струна звучит на ноте «до» первой октавы. Максимальное отклонение точек струны от положения равновесия равно и_тах = 2 мм. Найдем максимальную скорость и ускорение точек струны.

Закон колебания струны имеет вид (ср. (2.53)):

откуда находим скорость и ускорение точек струны:

По условию 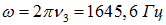(см. пример 3.). Максимальные значения скорости и ускорения равны:

Сложение гармоник

Выше мы уже занимались сложением колебаний, и теперь нам предстоит проделать то же самое, но для каждой точки колеблющейся струны.

Движение струны при возбуждении основной (первой) гармоники, показано на рис. 2.10–1. В начальном положении (линия отмечена красным цветом) точки струны имеют максимальное отклонение от положения равновесия. Под действием силы упругости они начинают двигаться (на рисунке – вертикально вниз), и форма струны через 1/8 периода показана линией зеленого цвета. Через четверть периода струна приходит в положение равновесия (линия черного цвета), но ее элементы имеют некоторые скорости, и потому в положении равновесия не задерживаются. Еще через 1/16 периода они оказываются в положении, показанном линией синего цвета, а через половину периода струна снова приобретает максимальное отклонение (пунктирная линия красного цвета), но в другую сторону, после чего процесс повторяется в обратном направлении. Так происходит колебание в стоячей волне, соответствующее первой гармонике, частоту которой мы обозначаем n₁.

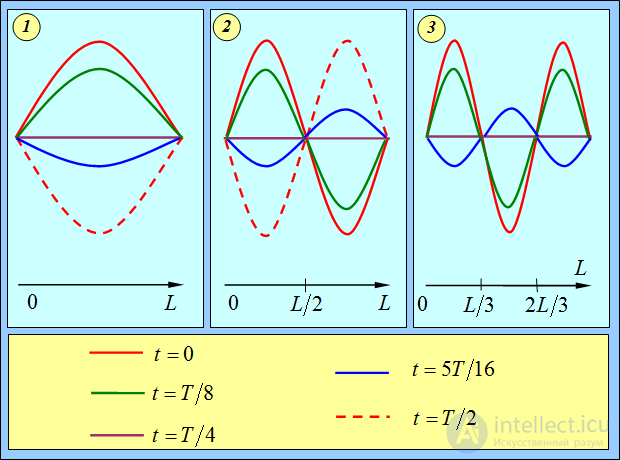
Рис. 2.10. Колебания струны:
1 – первая гармоника; 2 – вторая гармоника; 3 – третья гармоника;

Но на струне, как мы уже знаем, могут возникать колебания и других гармоник. Вторая гармоника показана на том же рис. 2.10–2. Использование тех же обозначений позволяет не описывать процесс колебаний столь же детально. Заметим, что в этом случае имеется одна неподвижная точка (ее называют узлом) в середине струны. Поскольку узел все равно не движется, можно представить себе, что мы закрепили среднюю точку. И тем самым, не изменив частоты издаваемого звука, в два раза укоротили струну. Стало быть, частота колебаний ровно в два раза превышает частоту основной гармоники: 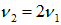. Этот результат мы уже получали другим способом.

На рис. 2.10–3 показаны колебания той же струны при возбуждении третьей гармоники. Здесь уже существует два узла, и издаваемый звук соответствует основному колебанию струны, укороченной в три раза (или, что то же самое, второй гармонике струны, длина которой составляет 2/3 исходной): .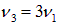

Колебания струны для первых трех гармоник показаны на рис. 2.11.

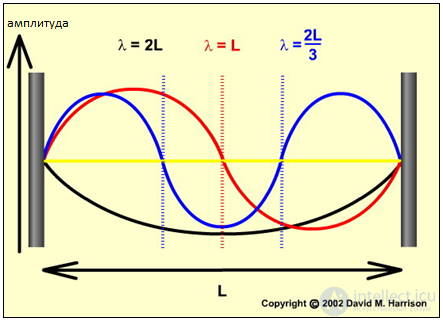
Рис. 2.11. Колебания струны для первых трех гармоник

На обсуждавшихся рисунках гармоники показаны без учета их амплитуд, то есть без учета их относительного вклада. На самом деле вклад гармоник может быть различным, так что в общем случае результирующее колебание получается сложением всех гармоник, каждая из которых представлена уравнением, аналогичным (2.59):

Здесь мы уже учли, что частоты и волновые числа принимают дискретный ряд значений; коэффициенты 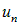– это амплитуды соответствующих гармоник. Заметим, что в множителе с зависимостью от времени мы заменили синус косинусом, то есть сдвинули точку отсчета времени. Теперь в момент t = 0 скорости всех точек струны равны нулю.

На практике приходится решать обратную задачу: находить коэффициенты 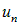по известному результирующему колебанию. Численные значения 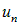зависят от способа возбуждения струны, например, от ее начальной формы 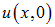. Если нам задана функция 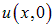, то для нее из (2.62) следует разложение:

которое известно в математике как разложение в ряд Фурье. Там же доказывается теорема, что коэффициенты и_п однозначно восстанавливаются по функции :

От величины примеси высших гармоник зависит форма колеблющейся струны. На рис. 2.12 показан вид колеблющейся струны в разные моменты времени при двух способах ее возбуждения. В обоих случаях струне придается некая начальная форма, после чего она отпускается «на свободу» (оставаясь закрепленной на концах, разумеется).

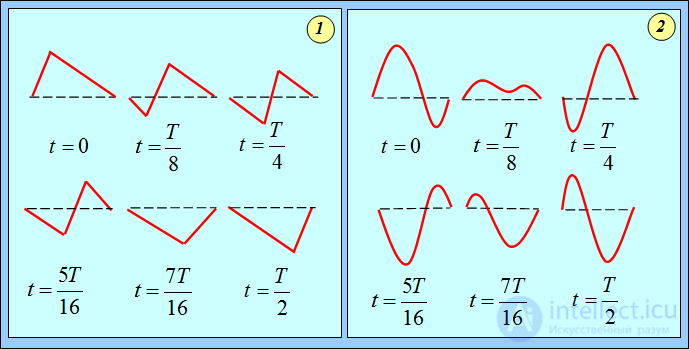
Рис. 2.12. Форма колеблющейся струны в различные моменты времени при разных формах струны в начальном состоянии:
1 – струна оттянута на расстоянии 0.1 ее длины; 2 – струне придана кусочно-синусоидная форма.

Мы рассматриваем два случая:

• в начальном положении струна оттягивается за точку, находящуюся на расстоянии 0.1 ее длины, считая от ее закрепленного конца;
• начальная форма струны описывается двумя синусоидами

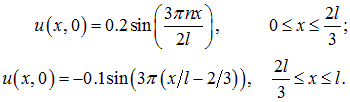
Второй пример носит явно модельный характер и дан для сравнения. Надо сказать, что придание струне какой-то начальной формы — не единственный способ возбуждения колебаний. Можно, например, задать начальное распределение скоростей (как происходит, скажем, в фортепиано, где молоточек ударяет по струне, находящейся в положении равновесия).

Мы все же ограничимся двумя описанными случаями. На рис. 22.6 показаны положения точек струны за половину периода колебаний основной гармоники, после чего процесс повторяется в обратном направлении. За время, равное периоду колебаний Т₁ первой гармоники, струна возвращается в исходное положение. Если струна настроена на ноту «до» первой октавы, то Т₁ = 3.82 мс.

элементы теории музыки

1. Спектр колебаний. Тембр звука, речь и пение

Причудливое изменение формы струны со временем мало что говорит нам о составе колебаний. Поэтому самой, быть может, важной характеристикой колебания является его спектр: диаграмма, показывающая относительный вклад каждой гармоники в полную интенсивность (энергию) колебаний, то есть функция

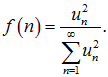
Спектр колебания также зависит от способа возбуждения струны. На рис. 2.13 приведен численный расчет спектра колебаний струны для обоих наших случаев. Темные столбики соответствуют «треугольной» начальной форме струны, а светлыми показан спектр колебаний струны, начальная форма которой составлена из кусков разных синусоид. По горизонтальной оси отложены номера гармоник, а высота столбиков по вертикальной оси дает относительную интенсивность соответствующих колебаний (то есть долю каждой из гармоник в полной интенсивности издаваемого струной звука).

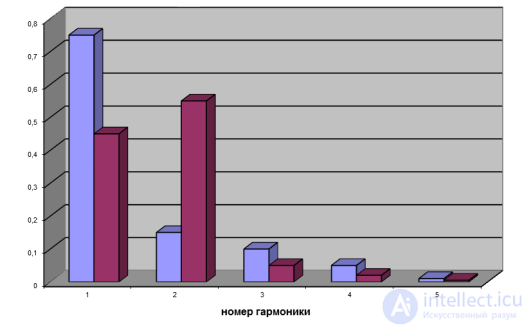
Рис. 2.13. Спектр колебаний струны (первые восемь гармоник) при разных способах возбуждения колебаний.
Синими столбиками показаны амплитуды обертонов при «треугольной» начальной форме струны,
а фиолетовыми — при «кусочно-синусоидальной» форме

Видно, что в первом случае наибольший вклад вносят первые четыре гармоники — на них приходится 97.9 % интенсивности звука, вклад следующих четырех гармоник уже невелик (2%), а на все остальные приходится лишь около 0.1% интенсивности. Конкретные числа здесь зависят от способа возбуждения струны, при ином методе они могут измениться. Например, при оттягивании струны за середину все четные гармоники просто отсутствуют в спектре, на долю первой приходится 98.55 %, на долю третьей — 1.22 %, пятой — 0.16 %, а оставшиеся 0.07 % — на долю всех остальных.

Во втором случае вклад второй гармоники даже больше вклада основ ной, заметны третья и, в меньшей степени, четвертая гармоники. В сумме вклад первых четырех гармоник составляет около 99.97 %, так что на все остальные приходится лишь 0.03 %.

Эти примеры демонстрируют общее правило: обычно возбуждаются низшие гармоники колебаний, а влияние высших уменьшается с ростом их номера. От наличия дополнительных гармоник в спектре колебаний (их называют обертонами) зависит окраска, тембр звука. По-разному воспринимается одна и та же нота, сыгранная на флейте, скрипке или гобое. Если бы звучала чистая нота, то никакого отличия одного инструмента от другого не было бы. Разнообразию музыкальных звуков мы обязаны обертонам. Степень их присутствия, помимо способа возбуждения вибратора, зависит также (и даже в гораздо большей степени) от резонатора инструмента. Так, при игре на скрипке в образовании звука принимает участие корпус инструмента, колеблющийся под действием колебаний струн, и объем воздуха внутри корпуса. Во-первых, тем самым усиливается звук инструмента: основной источник звука — тонкая струна, и сама по себе она не может привести в движение большую массу воздуха, чтобы звук дошел до слушателя. Во-вторых, на верхней деке скрипки возникают колебания, причем благодаря резонансу некоторые обертоны исходных колебаний струн усиливаются, а другие — гасятся. Резонаторы музыкальных инструментов выступают, таким образом, как преобразователи тембра исходного звука. Всем известно, что ценность инструмента, будь то скрипка или рояль, зависит не от качества натянутых в нем струн, а от особенностей строения их корпуса, дек. Искусство старых итальянских мастеров Страдивари, Амати, Гварнери, изготовивших прекрасные скрипки, альты и виолончели, состояло, в частности, в том, что они умели на практике добиваться оптимального спектра колебаний, что мы воспринимаем как божественного звучание их инструментов.

Области усиления высших обертонов называются формантами, и они определяют тембр того или иного инструмента. На рис. 2.14 показано разложение в спектр звуков рояля и кларнета.

Рис. 2.14. Спектр звука различных музыкальных инструментов

На спектре отчетливо видны форманты: скажем, шестая гармоника для рояля и восьмая–десятая — для кларнета. Именно они создают отличия в звучании этих инструментов.

Если перейти к голосу человека, то источником исходного звука является голосовая щель, колебания голосовых связок (то есть в сущности — тех же струн). На слух этот звук резко отличается от нормального, выходящего изо рта. Он носит «пищащий» характер и не имеет формы

продолжение следует...

Продолжение:

Часть 1 2. Волновые процессы и Элементы теории музыки
Часть 2 2.3. Энергия волны - 2. Волновые процессы и Элементы теории
Часть 3 2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -
Часть 4 2.5. Сферические волны - 2. Волновые процессы и Элементы теории
Часть 5 - 2. Волновые процессы и Элементы теории музыки
Часть 6 - 2. Волновые процессы и Элементы теории музыки
Часть 7 - 2. Волновые процессы и Элементы теории музыки

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.