2.3. Энергия волны - 2. Волновые процессы и Элементы теории

Это продолжение увлекательной статьи про волновые процессы.

...

Элементы теории музыки" >

(2.25)

Эта структура имеет максимумы смещений (рис. 2.7) в точках с координатами х_п, определяемыми из условия

Рис. 2.7. Смещение точек среды в момент времени t (сплошная кривая) и (пунктирная кривая).

Период повторения тех же смещений в пространстве есть расстояние между ближайшими максимумами:

Получаем в итоге:

Величина называется длиной волны.

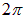Точнее, фазы колебаний в двух точках, отстоящих друг от друга на , отличаются на , что, учитывая периодичность синуса и косинуса, то же самое, что и равенство фаз. Напомним, что такие колебания чаще всего называют просто: синфазные колебания.

Если «сфотографировать» волну в близкий момент времени , то на снимке вся пространственная структура сдвинется как целое на расстояние . Скорость v называется фазовой скоростью волны, так как с такой скоростью движутся максимумы, минимумы и вообще все точки с данным значением фазы.

Если в общем случае фазу волны в точке с радиус-вектором в момент времени обозначить и ввести поверхность постоянной фазы, во всех точках которой фаза имеет одно и то же постоянное значение

,

то фазовую скорость волны можно определить так: фазовая скорость волны есть скорость точки поверхности постоянной фазы. Это скорость точки, принадлежащей поверхности постоянной фазы, сама эта поверхность не стационарна — ее точки перемещаются. В простейшем случае плоской волны вида поверхность постоянной фазы есть плоскость перпендикулярная оси ОХ и перемещающаяся вдоль этой оси с фазовой скоростью . Действительно:

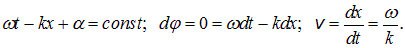
Используя (2.26) и (2.23), находим связь между характеристиками волны:

Здесь 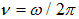— частота (в герцах) колебаний в волне.

Рис. 2.8.

Приведем численные примеры. Волна сгущений и разрежений в газе есть продольная упругая волна. Используя уравнение Менделеева-Клапейрона для газового состояния, можно записать скорость звуковой волны в газе (2.8) в виде:

где М — молярная масса, т — масса молекул, а T — абсолютная температура газа. С другой стороны, среднеквадратичная скорость молекул газа также определяется его абсолютной температурой

откуда

Иными словами, скорость звука в газе по порядку величины совпадает со скоростью теплового движения молекул. Молярная масса воздуха М=29·10^-3 кг/моль, показатель адиабаты . Подставляя эти значения в (2.28), находим скорость звука в воздухе при комнатной температуре (T = 20 °С = 293 К):

Человеческое ухо воспринимает частоты в диапазоне от 20 Гц до 20 кГц. Соответствующие длины волн равны:

для низких частот и

— для высоких.

Для стали модуль Юнга равен Е = 20.6·10¹⁰ Н/м², модуль сдвига G = 8·10¹⁰ Н/м², а плотность 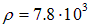. Соответственно, получаем из (2.14), (2.15) скорости распространения продольных и поперечных колебаний в стали :

Наконец, для воды роль модуля Юнга играет величина, обратная сжимаемости k=0.47·10^-9 Па^-1. Плотность воды кг/м³. Для скорости звука в воде получаем тогда:

Звук той же частоты будет иметь в воде и воздухе разные длины волн. Так, для кГц получаем длину волны в воде:

что надо сравнить с мм в воздухе.

Рассмотрим несколько примеров для оценки длины звуковой волны в различных средах.

Пример 1. Для диагностики опухолей в мягких тканях применяется ультразвук с частотой 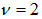МГц. Найдем длину ультразвуковой волны в воздухе и в мягких тканях, где скорость распространения звука равна 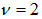МГц = 1.5 км/с.

Длина ультразвуковой волны в воздухе

В мягких тканях длина ультразвуковой волны равна

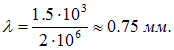
Как мы увидим в дальнейшем, длина волны любого излучения накладывает естественный предел на размеры объектов, которые можно различить с его помощью. Данный пример показывает, что диагностика опухолей, размеры которых меньше миллиметра, с помощью ультразвука затруднительна.

Пример 2. Летучая мышь использует для ориентирования ультразвук с частотой кГц. Определим размеры препятствий, которые заведомо не будут замечены летучей мышью и ответим на тот же вопрос в отношении дельфинов, которые также используют эти частоты.

Длина волны, испускаемой летучей мышью, равна

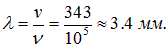
Препятствия меньших размеров заведомо не могут быть замечены мышью с помощью испускаемой ультразвуковой волны.

Для дельфинов ответ иной из-за другой скорости распространения звука в воде. Скорость звука в воде 1.46 км/с. Тогда

Таким образом, летучая мышь может обнаружить насекомых, а дельфин — небольших рыбок.

Пример 3. Альпинист, спускающийся с отвесной скалы, висит на веревке длиной 30 м. Страхующий его партнер подает ему сигнал, дергая веревку. Найдем, за какое время сигнал достигнет альпиниста. Масса альпиниста 80 кг, масса одного метра веревки равна 75 г.

Так как нам дана линейная плотность веревки 7.5·10^-2 кг/м и сила ее натяжения Т = тg, то по формуле (2.3) находим скорость распространения колебаний:

Отсюда определяем время прохождения сигнала:

2.3. Энергия волны

Рассмотрим для примера звуковую волну. Элемент объема на рис. 2.2. имеет кинетическую энергию:

При его деформации в данном объеме газа запасается потенциальная энергия П. Рассматривая колебания поршня, мы получили выражение (1.13) для силы упругости при перемещении поршня на расстояние х:

Этот закон аналогичен закону Гука для силы упругости при сжатии или растяжении пружины. Следовательно, потенциальная энергия газа равна в данном случае

Произведение равно изменению объема газа под поршнем. Поэтому (3.35) можно записать в виде:

Применим это выражение к объему газа в звуковой волне. Давление в стационарном состоянии мы обозначили . Объем в стационарном состоянии равен . Изменение объема при колебаниях равно

Получаем тогда для потенциальной энергии данного объема газа:

Сумма кинетической и потенциальной энергии равна полной энергии данного объема. Плотность энергии w в волне получаем, разделив полную энергию на величину объема:

Учитывая, что фазовая скорость волны равна

записываем (2.38) в виде:

Точно такое же выражение получается для волны в твердом теле (неважно, продольной ли, поперечной ли) и для волны вдоль струны.

Подставляя сюда решение (2.22)

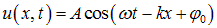
для монохроматической волны и учитывая соотношение

получаем для объемной плотности кинетической и потенциальной энергий одинаковые выражения

так что их сумма есть

Плотность энергии волны различна в разных точках пространства и в разные моменты времени. Зафиксируем какую-то точку х и усредним плотность энергии в данной точке по времени. Среднее значение квадрата синуса равно 1/2. Получаем тогда, что

Таким образом, среда обладает полным запасом энергии, плотность которой пропорциональна плотности среды, квадрату циклической частоты и квадрату амплитуды. Напомним, что для колебания системы с одной степенью свободы энергия колебания также была пропорциональна квадрату частоты и квадрату амплитуды колебания, а на месте плотности, — стояла масса колеблющегося тела.

Если вернуться к выражению (2.40) для мгновенного значения плотности энергии, то легко убедиться, что любое взятое значение плотности энергии, например, ее максимум

перемещается вдоль оси х с фазовой скоростью волны скоростью v. Иными словами, волна переносит энергию. Эта энергия доставляется, естественно, от источника колебаний. Можно ввести также вектор плотности потока энергии

модуль которого численно равен энергии, переносимой в единицу времени через единичную площадку, ортогональную направлению распространения волны. Отметим, что приведенные выше соотношения предполагают равенство скорости переноса волной энергии фазовой скорости волны. Это имеет место лишь в том случае, когда нет дисперсии, то есть фазовая скорость волны не зависит от ее волнового числа, а именно, когда .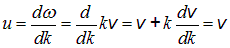

Применения к звуковой волне

Смещение частиц газа описывается стандартным решением:

где фазовая скорость

Под р и понимаются давление и плотность невозмущенного волной газа.

Смещение частиц приводит к появлению избыточного давления

Здесь мы использовали соотношение (2.4).

Учитывая, что

формулу (2.42) можно переписать в виде:

Заметим, что колебания давления сдвинуты на по отношению к колебаниям смещения частиц газа. При максимальном смещении

давление равно стационарному значению, то есть

Наоборот, амплитуда давления достигает максимума при нулевом смещении частиц газа.

Интенсивность волны, так же, как и объемная плотность энергии, пропорциональна квадрату амплитуды.

Звуковые волны принято характеризовать уровнем громкости L, измеряемым в децибелах (дБ). Связь уровня громкости с интенсивностью звуковой волны дается формулой:

где

Выбор I₀ связан с порогом слышимости в области частот 1 000 Гц – 4 000 Гц, к которым наиболее восприимчиво ухо человека. Таким образом, при I = I₀ уровень громкости полагается равным нулю. При интенсивностях волны порядка

волна перестает восприниматься как звук, вызывая только ощущение боли. Этому соответствует уровень громкости

Найдем связь между интенсивностью звуковой волны, избыточным давлением , создаваемым ею, и смещениями частиц газа. Амплитуда колебаний давления в волне равна (см. (2.43)):

откуда

Интенсивность волны выражаем также через амплитуду давления:

Отсюда находим избыточное давление в звуковой волне:

Учитывая, что плотность воздуха при нормальных условиях равна кг/м³, получаем амплитуду колебаний давления на болевом пороге (L = 120 дБ, I = 1Вт/м²):

Амплитуда смещения частиц газа зависит при этом от частоты:

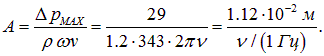
Отсюда следует, что при громкости L = 120 дБ и частоте n = 20 Гц смещение составляет А = 5.6·10^-4 м = 0.56 мм, а на частоте n = 20 кГц — А=5.6·10^-7 м = 0.56 мкм.

Найдем теперь амплитуду колебания скорости частиц газа:

Она не зависит от частоты волны и при громкости L = 120 дБ равна:

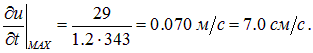
В таблице 1 представлены значения уровня громкости для некоторых звуков, с помощью которых можно найти избыточное давление, смещения и скорости частиц газа в иных случаях.

Таблица 1

Уровни громкости некоторых звуков

Звук	L, дБ
Шелест

продолжение следует...

Продолжение:

Часть 1 2. Волновые процессы и Элементы теории музыки
Часть 2 2.3. Энергия волны - 2. Волновые процессы и Элементы теории
Часть 3 2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -
Часть 4 2.5. Сферические волны - 2. Волновые процессы и Элементы теории
Часть 5 - 2. Волновые процессы и Элементы теории музыки
Часть 6 - 2. Волновые процессы и Элементы теории музыки
Часть 7 - 2. Волновые процессы и Элементы теории музыки