- 2. Волновые процессы и Элементы теории музыки

Это окончание невероятной информации про волновые процессы.

...

волн движение в направлении, ортогональном распространению волны, не приводило к сдвигу частот. Этот эффект прямо связан с релятивистским замедлением времени в движущейся системе отсчета: наблюдатель на ракете видит увеличение частоты излучения или, в общем случае, ускорение всех процессов, происходящих на Земле.

Найдем теперь фазовую скорость волны

в движущейся системе отсчета. Имеем из преобразований Лоренца для волнового вектора:

Подставим сюда соотношение:

Получаем:

Отсюда находим скорость волны в движущейся системе отсчета:

Мы обнаружили, что скорость волны в движущейся системе отсчета не изменилась и по-прежнему равна скорости света с. Отметим все же, что, при корректных выкладках, это не могло не получиться, так как инвариантность скорости света (электромагнитных волн) в вакууме есть основной постулат теории относительности уже «заложенный» в использованные нами преобразования Лоренца для координат и времени (3.109).

Пример 1. Фотонная ракета движется со скоростью V = 0.9 с, держа курс на звезду, наблюдавшуюся с Земли в оптическом диапазоне (длина волны 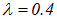мкм). Найдем длину волны излучения, которую будут наблюдать космонавты.

Длина волны обратно пропорциональна частоте колебаний. Из формулы (2.115) для эффекта Доплера в случае сближения источника света и наблюдателя находим закон преобразования длин волн:

откуда следует результат:

По рис. 2.28 определяем, что для космонавтов излучение звезды сместилось в ультрафиолетовый диапазон.

Энергия и импульс электромагнитного поля

Объемная плотность энергии w электромагнитной волны складывается из объемных плотностей 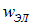электрического и 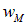магнитного полей:

Учитывая связь векторов Е и Н, получим, что плотности энергии электрического и магнитного полей в каждый момент времени одинаковы, то есть 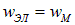. Следовательно, w можно представить в виде:

Если умножить плотность энергии w на скорость электромагнитной волны в среде

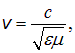
то получим модуль плотности потока энергии:

Так как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора

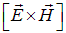
совпадает с направлением распространения волны, то есть с направлением переноса энергии, а модуль этого вектора равен ЕН. Следовательно, вектор плотности потока электромагнитной энергии, называемый вектором Умова-Пойнтинга, имеет вид:

Как и для упругих волн, интенсивность электромагнитной волны — это среднее значение плотности потока энергии:

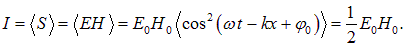
С учетом (2.107) между Е₀ и Н₀ получаем

Как и в упругой (звуковой) волне,

Пример 2. Интенсивность солнечного излучения, падающего на Землю, составляет I = 1.4 кВт/м² (солнечная постоянная). Найдем среднюю амплитуду колебаний E₀ вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H₀ и вектора магнитной индукции B₀ в волне.

Ответ находим сразу из уравнений (3.127), где полагаем :

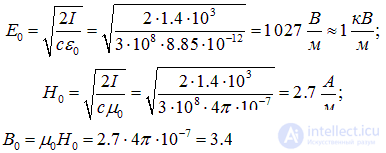
Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:

Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время площадка получила от волны энергию . Тогда переданный площадке импульс равен

На площадку действует со стороны волны сила

Давление Р, оказываемое волной, равно

Если средняя плотность энергии в волне равна , то на площадь А за время 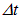попадет энергия из объема 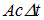и

Отсюда находим давление электромагнитной волны (света):

Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.

Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:

Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.

Площадь сечения пучка лазерного излучения

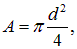
интенсивность излучения

Отсюда находим:

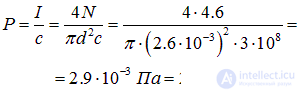
Исследование, описанное в статье про волновые процессы, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое волновые процессы, элементы теории музыки, электромагнитные волны и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Колебания и волны (Оптика, акустика и радиофизика)

Продолжение:

Часть 1 2. Волновые процессы и Элементы теории музыки
Часть 2 2.3. Энергия волны - 2. Волновые процессы и Элементы теории
Часть 3 2.4. Об этом говорит сайт https://intellect.icu . Стоячие волны -
Часть 4 2.5. Сферические волны - 2. Волновые процессы и Элементы теории
Часть 5 - 2. Волновые процессы и Элементы теории музыки
Часть 6 - 2. Волновые процессы и Элементы теории музыки
Часть 7 - 2. Волновые процессы и Элементы теории музыки