Лекция
Привет, Вы узнаете о том , что такое схема сонга, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое схема сонга , настоятельно рекомендую прочитать все из категории Шифры в криптографии.
схема сонга — алгоритм, реализующий шифрование и поиск по зашифрованным данным. Разработан Dawn Xiaodong Song, David Wagner, Adrian Perrig.
Эта работа была частью магистерской диссертации Технического университета Дрездена под руководством доктора Йозефа Спиллнера и Мартина Бека.
В этой статье авторы разрабатывают набор алгоритмов, позволяющих выполнять поиск по зашифрованным данным. Эти алгоритмы обеспечивают линейный поиск (O (n)) для каждого документа и вносят относительно небольшие накладные расходы на пространство. Также включены доказательства безопасности их модели, которые показывают, что сервер, на котором размещены данные, «не может ничего узнать об открытом тексте, учитывая только зашифрованный текст».
Сначала определим проблему поиска по зашифрованным
данные.
Предположим, у Алисы есть набор документов, и она хранит их.
на ненадежном сервере Боб. Например, Алиса могла быть
мобильный пользователь, который хранит свои сообщения электронной почты на ненадежном
почтовый сервер. Поскольку Бобу не доверяют, Алиса хочет зашифровать свои документы и сохранить зашифрованный текст только на Бобе.
Каждый документ можно разделить на «слова». Каждое слово'
может быть любой токен; это может быть 64-битный блок, английский
слово, предложение или некоторая другая атомарная величина, в зависимости от
в интересующую область приложения. Для простоты мы обычно предполагаем, что эти «слова» имеют одинаковую длину (в противном случае
мы можем либо дополнить более короткие «слова», либо разделить более длинные «слова»
чтобы все "слова" имели одинаковую длину, или используйте некоторые
простые расширения для «слов» переменной длины; см. также раздел 5.3). Поскольку у Алисы может быть только низкая пропускная способность
сетевое соединение с сервером Боба, она хочет только
получить документы, содержащие слово
. Для достижения этой цели нам нужно разработать схему, чтобы
после выполнения определенных вычислений над зашифрованным текстом,
Боб может с некоторой вероятностью определить, содержит ли каждый документ слово
ничего не изучая.
Кажется, есть два типа подходов. Одна из возможностей - создать индекс, который для каждого слова
представляет интерес,
перечисляет документы, содержащие
. Альтернативой является выполнение последовательного сканирования без индекса. Преимущество
использование индекса - это то, что он может быть быстрее, чем последовательный
сканировать, когда документы большие. Недостаток
использование индекса заключается в том, что сохранение и обновление индекса может быть
существенных накладных расходов. Итак, подход к использованию индекса
больше подходит для данных, предназначенных в основном только для чтения.
Сначала опишем нашу схему поиска по зашифрованному
данные без индекса. Поскольку схемы на основе индексов кажутся
чтобы требовать менее сложных конструкций, мы отложим
обсуждение поиска по индексу до конца
бумага (см. раздел 5.4)
Наша схема требует нескольких фундаментальных примитивов
из классической криптографии с симметричным ключом. Потому что мы
докажет безопасность нашей схемы, мы используем только примитивы с
четко определенное понятие безопасности. Мы перечислим здесь необходимые примитивы, а также рассмотрим стандартные определения безопасности для них. Определения можно пропустить
в первом чтении для тех, кто не интересуется нашими теоретическими
доказательства безопасности.
Мы принимаем стандартные определения безопасности из
литература по доказуемой безопасности , и мы измеряем силу
криптографических примитивов с точки зрения ресурсов
нужно было их сломать. Мы скажем, что атака прорывается
криптографический примитив, если алгоритм атаки успешен
в нарушении примитива с ресурсами, указанными, и
мы говорим, что криптопримитив безопасен, если нет алгоритма, который может его взломать. Пусть
Взаимодействие с другими людьми
- произвольный алгоритм, и пусть и - распределены случайные величины. Отличительная вероятность
- иногда называемого преимуществом - для и
является
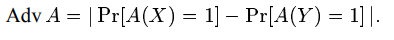
На этом фоне наш список необходимых примитивов выглядит так:
следующее:
1. Псевдослучайный генератор 1, т. Е. Потоковый шифр.
Мы говорим, что 12
354 6
является & 78: 9 -защищенным псевдослучайным генератором, если каждый алгоритм с временем выполнения не более 7 имеет преимущество Adv <; = 9. В
преимущество противника определяется как
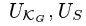- случайные величины , распределенные равномерно на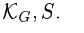 
.
2. Псевдослучайная функция K. Мы говорим, что KL
M3ON P
Q SR - это -78: TU V9 - безопасная псевдослучайная функция.
если каждый алгоритм оракула делает не более Т оракула
запросов и с временем выполнения не более 7 имеет преимущество
Adv; 9. Преимущество определяется как Adv <
"! + #,% N
.'C)! $ #%
Взаимодействие с другими людьми
('где представляет
случайная функция, выбираемая равномерно из множества
все карты из Q
к R
, и где вероятности
взял на себя выбор
и .
3. Псевдослучайная перестановка, т.е. блочный шифр.
Мы говорим что
3 пол.
является -78: TU V9 -защищенная псевдослучайная функция, если каждый алгоритм оракула делает
самое большее количество запросов к Oracle и самое большее время выполнения
7 имеет преимущество Adv; 9. Преимущество определено
как Adv>! $ #.%
Взаимодействие с другими людьми
Взаимодействие с другими людьми
. ' )
! $ #,%
Взаимодействие с другими людьми
Взаимодействие с другими людьми
('
где представляет собой случайную перестановку, выбранную равномерно из множества всех биекций на, и где
вероятности берутся за выбор
и.
Обратите внимание, что противнику дается оракул как для шифрования, так и для дешифрования; это соответствует
адаптивная модель атаки с выбранным открытым текстом / зашифрованным текстом.
В общем, интуиция подсказывает, что -78: TU V9 -security представляет собой
устойчивость к атакам, использующим не более 7 автономных работ и при
большинство T адаптивных запросов с выбранным текстом.
Конечно, нет принципиальной необходимости в трех отдельных примитивах, поскольку на практике все три могут быть построены
всего одного стандартного примитива. Например, при любом
блочный шифр, мы можем построить псевдослучайный генератор, используя режим счетчика или псевдослучайную функцию, используя
CBC-MAC .
Мы будем использовать следующие обозначения. Если
3 P Q R
представляет собой псевдослучайную функцию или перестановку, мы
напишите результат подачи на ввод с помощью ключа
3. Мы пишем E для конкатенации и,
и! для побитового XOR для и. В оставшейся части статьи мы полагаем 1
34 Q # "быть псевдослучайным
генератор для некоторых
, К
3N P Q
- псевдослучайная функция, и
3 $ P%
- псевдослучайная перестановка. Обычно у нас будет Q
'&
, Р
Взаимодействие с другими людьми
, а Q
P R
Взаимодействие с другими людьми
.
В этом разделе мы представляем наше решение для поиска
с последовательным сканированием. Начнем сначала с базовой схемы
и показать, что его алгоритм шифрования обеспечивает доказуемую
секретность. Затем мы покажем, как можно расширить первую схему
для обработки управляемого поиска и скрытого поиска. Мы описываем нашу окончательную схему, которая удовлетворяет всем свойствам, которые мы
упоминалось ранее, включая изоляцию запроса в конце.
4.1 Схема I: Базовая схема
Алиса хочет зашифровать документ, содержащий
последовательность слов) (, /. /. /
"
. Интуитивно схема
работает, вычисляя побитовое исключающее ИЛИ (XOR)
открытый текст с последовательностью псевдослучайных битов,
особая структура. Эта структура позволит искать по
данные , не раскрывая ничего другого о открытом тексте.
Более конкретно, базовая схема выглядит следующим образом. Алиса
генерирует последовательность псевдослучайных значений 6 (
, /. /. / 6
"
используя некоторый потоковый шифр (а именно, генератор псевдослучайных 1), где каждые 6 + * имеют длину) бит. Зашифровать
-битовое слово *
появляется в позиции, Алиса берет
псевдослучайные 6 *
, наборы -
*
. Об этом говорит сайт https://intellect.icu . 6 *
: K 0/6 *, и выходы
зашифрованный текст 1
*
* 2- *
. Обратите внимание, что только Алиса может генерировать псевдослучайный поток -
(
./,/./ 3- "
так что никто другой
можно расшифровать. Конечно, шифрование можно выполнить в режиме онлайн, поэтому
что мы шифруем каждое слово, когда оно становится доступным.
Существует некоторая гибкость в том, как ключи *
может быть выбран. Одна из возможностей - использовать тот же ключ
в каждой позиции в документе. Другой вариант - выбрать
новый ключ *
для каждой позиции независимо от всех остальных ключей.
В более общем плане, в каждой позиции Алиса может либо (а) выбрать
*
быть таким же, как некоторые предыдущие 4 (5;,), или (b) выбрать
*
независимо от всех предыдущих ключей. Мы увидим позже
как эта гибкость позволяет нам поддерживать множество интересных функций.
Базовая схема обеспечивает доказуемую секретность, если псевдослучайная функция K и псевдослучайный генератор 1
безопасны. Под этим мы подразумеваем, что в каждой позиции, где
*
неизвестно, значения -
*
неотличимы от
действительно случайные биты для любого вычислительно ограниченного противника. Формализуем теорему, как показано ниже.
Теорема 4.1. Если K - это & 78
: 9 N -защищенный псевдослучайный
функция, а 1 - безопасный генератор псевдослучайных сигналов & 78: 94, и если ключевой материал выбран, как описано выше,
то описанный выше алгоритм генерации последовательности - (
././,/M - "
is a -7) 76: 9 -безопасный псевдослучайный
генератор, где 9 I
98 "9N #: 94:
Взаимодействие с другими людьми
)
Взаимодействие с другими людьми
Взаимодействие с другими людьми
Q
и
постоянная 6
незначительно по сравнению с 7.
Другими словами, мы ожидаем, что базовая схема будет хорошей.
для шифрования примерно до
макс <; '&> =? A @ слова, если
псевдослучайная функция и псевдослучайный генератор
достаточно безопасны. См. Приложение A для получения более подробной информации.
точная формулировка теоремы и полное доказательство.
Базовая схема поддерживает поиск по зашифрованному тексту .
следующим образом: если Алиса хочет найти слово
,
она может сказать Бобу
и *
соответствует каждому месту, где слово
может возникнуть. Затем Боб может искать
для
в зашифрованном тексте, проверив, 1
* *
является
вида CB: K 0 / CB для некоторого B. Такой поиск может быть
выполняется за линейное время. На позициях, где работает Боб
не знаю *
, Боб ничего не узнает об открытом тексте. Таким образом,
схема допускает ограниченную форму контроля: если только Алиса
хочет, чтобы Боб мог выполнять поиск по первой половине зашифрованного текста, Алиса должна открывать только *
соответствующий
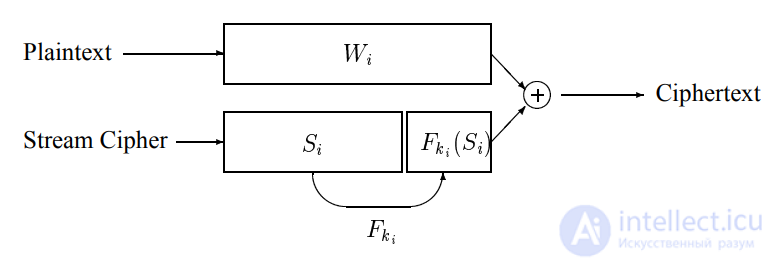
Рисунок 1. Базовая схема
эти места и ни один из *
используется во второй половине
зашифрованный текст.
Как было описано выше, основная схема не очень удовлетворительна: если Алиса хочет помочь Бобу найти слово
,
либо Алиса должна раскрыть все *
(таким образом потенциально раскрывая весь документ), или Алиса должна знать заранее
какие места
может появиться в (что, кажется, побеждает
цель удаленного поиска). Однако мы увидим
Далее, как решить эту проблему.
4.2 Схема II: Контролируемый поиск
Пусть F
3N P
3N - дополнительная псевдослучайная функция, которая будет вводиться независимо от K.
Основная идея - выбрать наши ключи как *
*.
Мы требуем, чтобы
выбирается равномерно случайным образом в 3 с помощью
Алиса и никогда не раскроется. Затем, если Алиса желает разрешить
Боб искать слово
, она показывает
и
к
ему. Это позволяет Бобу определить все места, где
может произойти, но ничего не показывает на локациях
, где *
. Это достигает нашей желаемой цели контролируемого поиска. Показываем правильность такого подхода.
в следующей теореме.
Теорема 4.2. Предположим, что K - & 78 "
V9 N -защищенная псевдослучайная функция, составляет -78 "
V9 -защищенная псевдослучайная функция, а 1 - -78: 9 4 -защищенный генератор псевдослучайных сигналов.
Если ключевой материал выбран, как описано выше, то
описанный выше алгоритм генерации последовательности
- (
, /. /. / M 3- "
будет & 7) 6
V9 "! -Защищенный псевдослучайный
генератор, где 9 "!
8 9К: 9: 94:
Взаимодействие с другими людьми
)
Взаимодействие с другими людьми
Взаимодействие с другими людьми
Q
.
Это показывает, что наша схема контролируемого поиска
примерно так же хорош, как и базовая схема, если базовые примитивы безопасны. См. Приложение A для доказательства, а также
более точная формулировка.
Возможны различные расширения этой идеи. Если документ, который нужно зашифровать, состоит из серии глав,
альтернативный подход - сгенерировать ключ *
за слово
Взаимодействие с другими людьми
в главе 1 как *
# 3 C1
. Это позволяет Алисе контролировать, в каких главах Боб может искать, а также
контролировать, какие слова Боб может искать.
Мы можем развить эту идею еще дальше, используя иерархическую схему управления ключами. Наборы Алисы *
"$? 01 $
и %
#
*. Тогда она может раскрыть либо
(1)
; '& (
(*) =? A1 $ за каждую интересующую главу или (2)
Взаимодействие с другими людьми
Взаимодействие с другими людьми
сама, если она желает кратко разрешить Бобу
искать
во всех главах.
Эта схема по-прежнему не поддерживает скрытые поисковые запросы:
чтобы Боб мог найти место, где слово
Взаимодействие с другими людьми
появляется, Алиса должна раскрыть
Бобу. Мы увидим дальше
что эта проблема может быть легко решена
фиксированный.
Предположим, Алиса теперь хочет попросить Боба найти
слово
но она не желает раскрывать
Бобу. Мы
предложить простое расширение к указанной выше схеме для поддержки
эта цель.
Алисе следует просто предварительно зашифровать каждое слово
из
чистый текст отдельно с использованием детерминированного алгоритма шифрования #. Обратите внимание, что нельзя использовать случайность, и вычисление # может зависеть только от
и не должен зависеть от позиции в документе
где находится. Итак, мы можем подумать об этом предварительном шифровании
шаг как шифрование ECB слов документа с использованием некоторого блочного шифра. (Конечно, если слово очень
long, внутренне карта может быть реализована с помощью CBCencrypting *
с постоянным IV или каким-то другим, но
Дело в том, что этот процесс должен быть одинаковым на всех позициях
документа).
*
*.
После фазы предварительного шифрования Алиса имеет последовательность
-зашифрованные слова
(
, /. /. / "
. Теперь она пост-шифрует
эта последовательность с использованием конструкции потокового шифра, описанной выше, для получения 1
*
Взаимодействие с другими людьми
* -
*
, где
* # * и -
*. 6 *
ВК / - * 3 8 /
Искать слово
, Алиса вычисляет
#
Взаимодействие с другими людьми
и
# & и отправляет -
Бобу. Обратите внимание, что это
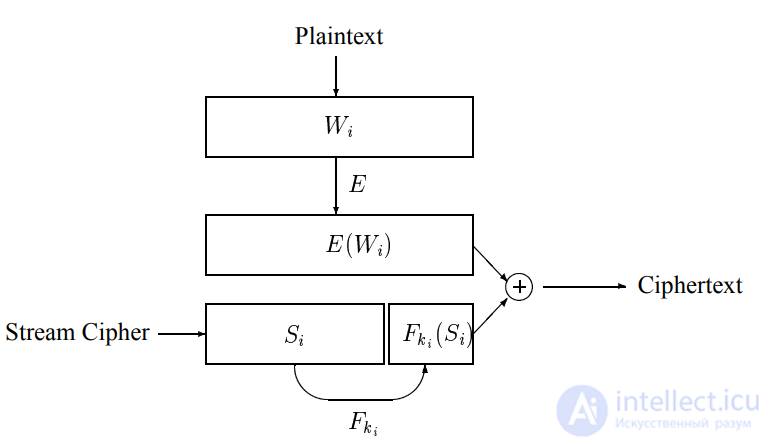
Рисунок 2. Схема скрытого поиска
позволяет Бобу искать
не раскрывая
сам. Это
легко видеть, что эта схема удовлетворяет скрытому поиску
свойство, если предварительное шифрование является безопасным.
4.4 Схема IV: Окончательная схема
Внимательные читатели могли заметить, что Схема III на самом деле страдает от небольшого недостатка: если Алиса генерирует
ключи *
в качестве *
C * тогда Алиса больше не может
восстановить открытый текст только из зашифрованного текста, потому что она
необходимо знать # * (точнее, последний
биты *), прежде чем она сможет расшифровать. Это побеждает
цель схемы шифрования, потому что даже законные
Принципалы с доступом к ключам дешифрования не смогут
расшифровать. (Схема II также имеет аналогичную неадекватность, но
как мы покажем ниже, лучший способ исправить это - ввести
предварительное шифрование, как на схеме III.)
Теперь мы покажем простое решение этой проблемы. В фиксированном
схему, мы разбиваем предварительно зашифрованное слово
* # *
на две части,
* *
V *, где
*
(соответственно
*
)
обозначает первые) биты (соответственно последние биты)
*
. Вместо
генерации *
C *, Алиса должна сгенерировать *
в качестве *
# *. Для расшифровки Алиса может сгенерировать 6 *
с помощью
псевдослучайный генератор (поскольку Алиса знает семя),
и с 6 *
она может выздороветь
*
XORing 6 + * против
первый) биты 1
*
. Наконец, знание
*
позволяет Алисе
вычислить *
и на этом закончим расшифровку.
Это исправление небезопасно, если *
Не зашифрованы, так как
может быть очень вероятно, что в некоторых случаях разные слова имеют
тот же первый (!) бит. Предварительное шифрование устранит
эта проблема, так как с большой вероятностью все
*
Являются
отчетливый. (Предполагая, что предварительное шифрование является псевдослучайной перестановкой, тогда из-за парадокса дня рождения [15],
вероятность того, что хотя бы одна коллизия произойдет после шифрования
слов самое большее
Взаимодействие с другими людьми
)
; <& (
знак равно
/)
С этим исправлением полученная схема доказуемо безопасна,
и на самом деле мы также можем показать, что он обеспечивает изоляцию запросов, что означает, что даже когда один ключ *
раскрыто, нет
утечка дополнительной информации выходит за рамки возможности идентифицировать
позиции, где соответствующее слово *
происходит.
Теорема 4.3. Предположим, это & 78
: 9 -защищенная псевдослучайная перестановка, K равно -78 "
V9N - безопасный псевдослучайный
функция, является & 78 "
V9 -защищенная псевдослучайная функция, 1
является -78: 9 4 -защищенным псевдослучайным генератором, и мы выбираем
ключевой материал, как описано выше. Тогда описанный выше алгоритм генерации последовательности - (
, /. /. / M 3- "
буду
быть a & 7)! 6: 9! -защищенный псевдослучайный генератор, где
9! Взаимодействие с другими людьми
> 8,9 Н: 9: 9 4:
Взаимодействие с другими людьми
)
Взаимодействие с другими людьми
Взаимодействие с другими людьми
Q
.
Более того, если мы раскроем один *
и рассмотрим сокращенный
последовательность -
Взаимодействие с другими людьми
полученный путем отбрасывания всего -
4
значения в позициях, где 4 *
, то получаем a & 7) 6
: 9
! -безопасный
псевдослучайный генератор , где 9
! I9 "!: 9
:
Взаимодействие с другими людьми
Q
.
Строго говоря, доказательство теоремы на самом деле не требует псевдослучайной перестановки : если
обозначает отправку карты (с ключом)
к первому) бит
из #
, тогда мы сможем обойтись гораздо более слабым
предположение, что столкновения должны быть редкими. Как особый
случай, если первые биты (
)) можно показать как
псевдослучайная функция , то обязательно будет
требуемое свойство , и мы сможем доказать результат, аналогичный теореме 3. Это предполагает, что для предварительного шифрования
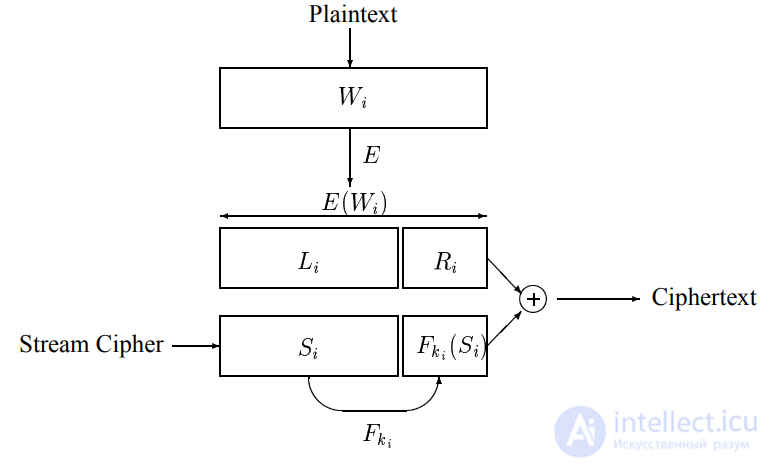
Рисунок 3. Окончательная схема длинных блоков может быть
нет, чтобы взять #
быть
инверсия битов шифрования CBC
под ключ
(с использованием постоянной IV).
После пословного шифрования Алиса также может изменить порядок
зашифрованный текст согласно некоторой псевдослучайной перестановке (известной только Алисе). В этом случае, когда Боб выполняет
поиск слова, он не сможет сказать позицию
где слово встречается в реальном открытом тексте.
Мы видим, что обновления в этой схеме просты. Например, если Алиса хочет добавить новый документ в папку Боба
хранилище данных, она может просто зашифровать их в соответствующем
способ и проинструктируйте Боба добавить его к уже сохраненному зашифрованному тексту. Более того, поскольку ключи могут быть сгенерированы иерархически из главного ключа, хранение и управление ключами
тоже очень удобно: Алисе нужно запомнить только одно
пароль, мастер-ключ.
Основная техника встраивания информации в
псевдослучайные потоки битов также могут представлять независимый интерес: мы предполагаем, что этот простой трюк может оказаться полезным
и для других приложений тоже.
Схемы, которые мы представили ранее, решают проблему поиска только одного слова. Мы показываем несколько примеров, чтобы проиллюстрировать, что реализовать относительно легко
более продвинутые функции поиска с использованием нашей схемы как
фундаментальный строительный блок.
Понятно, что мы легко можем поддержать расширенный поиск
запросы, использующие логические операторы (например,
и
),
запросы близости (например,
рядом
) и поиск по фразе
(например,
непосредственно предшествует
).
Мы также можем поддерживать поиск, если запрос задан как
регулярное выражение с использованием, например, подстановочных знаков в ограниченной форме.
Например, если Алиса хочет найти слово% -
'
,
тогда она может фактически сгенерировать 26 поисковых запросов вида
././,/*
. Однако количество необходимых запросов (и утечка информации на сервер) явно
резко увеличивается по мере того, как поисковое слово становится более общим.
Для многих приложений цель поиска - найти
документы, которые содержат определенное слово, где позиция или количество вхождений не имеют значения. Например, поиск по электронной почте - это такое приложение, в котором
запрос принимает форму «найти все письма от Джо». За это
приложения, предыдущие схемы поиска утекали информацию, так как сервер знал бы позиции слова
в документе, или, по крайней мере, частота слова в документе, если порядок слов зашифрован. Поскольку мы только
нужно знать, содержит ли данный документ слово,
мы можем использовать следующий трюк. Мы добавляем счетчик к каждому
word, который подсчитывает, сколько раз это слово встречается ранее в этом документе. Например, первое вхождение
слова «срочно» сохраняется как «срочно», второе появление - как
срочно и т. д. Это позволяет Алисе искать
только первое появление, если она хочет просто идентифицировать
документы, в которых встречается это слово; и Боб не получает
любую информацию о других позициях поискового запроса в
документ. В качестве дополнительной функции эта кодировка позволяет Алисе искать документы, содержащие или более
вхождения слова
путем поиска)
Взаимодействие с другими людьми
В нашей схеме минимальная единица, которую мы можем найти, - это
отдельное слово. До сих пор мы предполагали, что открытый текст
легко разбивается на последовательность слов фиксированного
длина. Но это может быть не так в обычном текстовом документе.
Например, если минимальная единица поискового интереса - одна
Английское слово, тогда мы должны иметь дело с тем, что английский
слова различаются по длине.
Одна из возможностей - выбрать длинный блок фиксированного размера.
достаточно, чтобы вместить большинство слов. Слишком короткие слова
или слишком длинный может быть дополнен до кратного размера блока
с некоторым заранее определенным форматом заполнения. (Обратите внимание, что
заполнение не может быть случайным, так как Алиса должна знать
заполнение для выполнения поиска.) Однако такой
схема заполнения привела бы к неэффективности использования пространства. Также,
по соображениям безопасности мы не можем уменьшить длину слова ниже определенного предела.
Другое решение - использовать слова переменной длины. В этом
случае, для поддержки дешифрования с произвольным доступом, длина
каждое слово также должно быть сохранено вместе со словом. Один из естественных подходов - хранить поле длины перед каждым словом в
файл и склеить поле длины и слово как одно целое
слово для шифрования и поиска с использованием нашего стандарта
схемы.
Когда длина слов может быть разной, важно скрыть
информация о длине с сервера, потому что раскрытие
длина каждого слова может допускать статистические атаки. К счастью, в этом случае серверу не нужно знать
длины для выполнения поиска: он может просто сканировать
файл и проверьте соответствие на каждой возможной границе битов.
В этом случае стоимость каждого сканирования увеличивается, потому что
количество операций определяется битовой длиной
документ, а не количество блоков в документе. ЧАС
Тем не менее, такой подход может обеспечить лучшее пространство
эффективность по сравнению с блочно-ориентированной схемой.
Последовательное сканирование может быть недостаточно эффективным, если
размер данных большой. Для некоторых приложений, например больших
базы данных , распространенный метод ускорения поиска
заключается в использовании предварительно вычисленного индекса. Здесь мы показываем, как мы можем
отвечать на поисковые запросы с помощью зашифрованного индекса
без ущерба для безопасности.
Индекс содержит список ключевых слов; с каждым ключом
слово - это список указателей на документы, в которых ключевое слово
появляется. Ключевые слова - это интересные слова, которые Алиса может
хочу поискать позже. Алиса, безусловно, может построить индекс
ее открытых текстовых документов, а затем зашифровать открытый текст
и индекс и сохранить зашифрованный текст на Бобе. Интересный вопрос, как зашифровать индекс.
Наивным способом было бы просто зашифровать ключевые слова в
индекс и оставьте списки позиций незаполненными. Это делает
Бобу легко выполнять поисковые запросы от имени Алисы,
но также передает много информации Бобу и, следовательно, может
позволяют ему применять различные статистические атаки. Поэтому мы
отвергнуть этот наивный подход.
Простой способ - также зашифровать указатели документов в
каждый список в указателе. Следовательно, когда Боб ищет
Взаимодействие с другими людьми
и находит совпадение, он возвращает Алисе зашифрованный список
совпадающих позиций из индекса. Алиса может расшифровать
зашифрованные записи и отправьте Бобу еще один запрос на получение соответствующих документов. Одно возможное преимущество для
эта схема заключается в том, что запрос может быть встроен в другие
поисков, так что Боб может быть неуверен в корреляции поискового запроса и поискового запроса для
зашифрованный текст. Недостаток в том, что Алисе приходится тратить
дополнительное время туда и обратно для получения документов.
Если Алиса не хочет ждать дополнительной поездки туда и обратно
время , или если Алиса хочет, чтобы Боб объединил для нее результаты нескольких поисковых запросов, доступны и другие методы. Например, она может зашифровать список документов.
указатели в индексе с помощью ключа (связанных
, т.е.
(#
. Следовательно, когда Алиса хочет искать
за слово
, она раскроет
8 (Бобу.
чтобы Боб не мог проводить статистический анализ
index, лучше хранить списки указателей фиксированного размера
список. Для слов, которые появляются нечасто, Алиса может дополнить
список до фиксированного размера. Для более общих слов Алиса может
разбить длинный список на несколько списков фиксированного размера; тогда,
чтобы найти такое слово, Алисе нужно попросить Боба
выполнять и объединять несколько поисковых запросов параллельно. Примечание
что, сохраняя списки указателей в списке фиксированного размера, мы
в основном мешают Бобу изучать статистическую информацию по ключевым словам, которые он не искал. Для
ключевые слова , которые искал Боб, он все еще может
узнать некоторую статистическую информацию из схемы доступа Алисы. Это приемлемо с нашей точки зрения, поскольку Алиса
хочет только получить соответствующие документы в первую очередь .
Обратите внимание , что общий недостаток поиска по индексу заключается в том, что
всякий раз, когда Алиса меняет свои документы, она должна обновить
индекс . Существует компромисс между тем, сколько индексов обновляет Алиса, и тем, сколько информации Боб сможет обработать.
учиться. Например, если Алиса не изменяет список указателей документов для одной записи ключевого слова, когда она добавляет новый
документ в хранилище данных Боба, Боб сможет
Сообщите, что ключевое слово не появляется в новом документе.
Следовательно, Алисе необходимо обновить значительную часть индекса.
чтобы скрыть настоящие обновления, которые могут быть довольно дорогими. это
интересный исследовательский вопрос для разработки схем, которые
поддерживать более эффективные обновления.
Во всех наших схемах, позволяя Бобу искать слово
Взаимодействие с другими людьми
мы эффективно раскрываем ему список потенциальных мест
где
может произойти. Если мы позволим Бобу тоже искать
много слов, он может использовать статистические методы, чтобы
начните узнавать важную информацию о документах.
Одна из возможных защит - уменьшение (чтобы ложные совпадения
более распространены, и поэтому информация Боба о
открытый текст "зашумлен"), но мы не анализировали экономическую эффективность этого компромисса в каких-либо деталях.
Лучшая защита для Алисы - периодически менять
key, повторно зашифруйте все документы под новым ключом и измените порядок зашифрованного текста в соответствии с некоторой псевдослучайной перестановкой (известной Алисе, но не Бобу). Это поможет
запретить Бобу изучать корреляции или другие статистические
информация с течением времени. Этот метод также может быть полезен, если Алиса хочет скрыть от Боба места, где
искомое слово встречается в интересующих документах.
Во всех схемах, которые мы обсуждали до сих пор, мы должны
доверять Бобу возвращать все результаты поиска. Если Боб продержится
нам и возвращает только некоторые (но не все) результаты поиска,
Алиса не сможет это обнаружить. В рамках нашего интереса мы предполагаем, что Боб не ведет себя плохо.
качаться. Четное
когда присутствует этот тип атаки, можно комбинировать
наша схема с методами хэш-дерева [17] для обеспечения целостности данных и обнаружения таких атак, хотя полная
описание этой меры противодействия выходит за рамки
бумага.
Многие исследователи исследовали проблему обеспечения секретности и целостности при использовании ненадежного файла.
сервер или внешняя недоверенная память [5, 12, 1, 6]. Но насколько
как мы знаем, никакая предыдущая работа не предоставила решения для
поиск по зашифрованным данным. Также интенсивно изучаются безопасные многосторонние вычисления и незаметные функции (см.
например, [14, 8]). Мы считаем, что может быть решение
проблема поиска по зашифрованным данным с использованием многосторонних
вычисления, но это потребует больших накладных расходов, например, нескольких серверов. Нашему решению нужен только один сервер
для поиска по зашифрованным данным и, следовательно, более практичный
решение.
Несколько исследователей изучили личную информацию.
Проблема извлечения (PIR) , так что клиенты могут получить доступ к записям в распределенной таблице, не раскрывая, какие записи
они заинтересованы. Литература PIR обычно направлена на
очень строгие теоретико-информационные границы безопасности, которые
затрудняет поиск практических схем: схемы PIR часто требуют нескольких серверов, не участвующих в сговоре, потребляют большие
объемы пропускной способности , не гарантируют конфиденциальность
данных, не поддерживают частный поиск по ключевым словам и
не поддерживают контролируемый поиск или изоляцию запросов (но
см., например, [16, 13, 10, 7] для важных исключений, которые позволяют снять некоторые - но не все - из этих ограничений). В
Напротив, хотя наша схема не решает проблему PIR, ей нужен только один сервер (без непрактичного доверия
предположений), имеет низкую вычислительную сложность и поддерживает частный поиск по ключевым словам с очень высокой степенью безопасности.
характеристики.
Мы описали новые методы удаленного поиска о зашифрованных данных с использованием ненадежного сервера и предоставленных
доказательства безопасности полученных криптосистем. Наш
методы имеют ряд важных преимуществ: они
доказуемо безопасный; они поддерживают контролируемый и скрытый поиск
и изоляция запросов; они просты и быстры (точнее, для длинного документа шифрование и поиск
алгоритмам нужен только поточный шифр и блочный шифр
операции); и они не вводят почти никаких накладных расходов на пространство и связь. Наша схема также очень гибкая, и
его можно легко расширить для поддержки более расширенного поиска
запросы. Мы пришли к выводу, что это дает новый мощный
строительный блок для построения безопасных сервисов в
ненадежная инфраструктура.
Благодарности
Мы хотели бы поблагодарить Дуга Тайгара за его ценные предложения и советы. Мы также хотели бы поблагодарить Джона Кубятовича за поддержку работы над проблемой поиска по зашифрованным данным. Мы также хотели бы поблагодарить Боба
Бриско за полезные комментарии к статье.
Авторы: Дон Сяодун Сонг, Дэвид Вагнер и Адриан Перриг.
Данная статья про схема сонга подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое схема сонга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Шифры в криптографии
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Шифры в криптографии
Термины: Шифры в криптографии