Лекция
Привет, Вы узнаете о том , что такое криптосис rsa цифровая подпись, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое криптосис rsa цифровая подпись , настоятельно рекомендую прочитать все из категории Шифры в криптографии.
RSA – криптографическая система открытого ключа, обеспечивающая такие механизмы защиты как шифрование и цифровая подпись (аутентификация – установление подлинности). Криптосистема RSA разработана в 1977 году и названа в честь ее разработчиков Ronald Rivest, Adi Shamir и Leonard Adleman. Алгоритм RSA работает следующим образом: берутся два достаточно больших простых числа p и q и вычисляется их произведение n = p*q; n называется модулем. Затем выбирается число e, удовлетворяющее условию
1< e < (p - 1)*(q - 1) и не имеющее общих делителей кроме 1 (взаимно простое) с числом (p - 1)*(q - 1). Затем вычисляется число d таким образом, что (e*d - 1) делится на (p - 1)*(q – 1).
e – открытый (public) показатель
d – частный (private) показатель
(n; e) – открытый (public) ключ
(n; d). – частный (private) ключ.
Делители (факторы) p и q можно либо уничтожить либо сохранить вместе с частным (private) ключом. Если бы существовали эффективные методы разложения на сомножители (факторинга), то, разложив n на сомножители (факторы) p и q, можно было бы получить частный (private) ключ d. Таким образом надежность криптосистемы RSA основана на трудноразрешимой – практически неразрешимой – задаче разложения n на сомножители (то есть на невозможности факторинга n) так как в настоящее время эффективного способа поиска сомножителей не существует. Ниже описывается использование системы RSA для шифрования информации и создания цифровых подписей (практическое применение немного отличается).

Шифрование
Предположим, Алиса хочет послать Бобу сообщение M. Алиса создает зашифрованный текст С, возводя сообщение M в степень e и умножая на модуль n: C = M**e* (mod n), где e и n – открытый (public) ключ Боба. Затем Алиса посылает С (зашифрованный текст) Бобу. Чтобы расшифровать полученный текст, Боб возводит полученный зашифрованный текст C в степень d и умножает на модуль n:
M = c**d*(mod n); зависимость между e и d гарантирует, что Боб вычислит M верно. Так как только Боб знает d, то только он имеет возможность расшифровать полученное сообщение.


Цифровая подпись
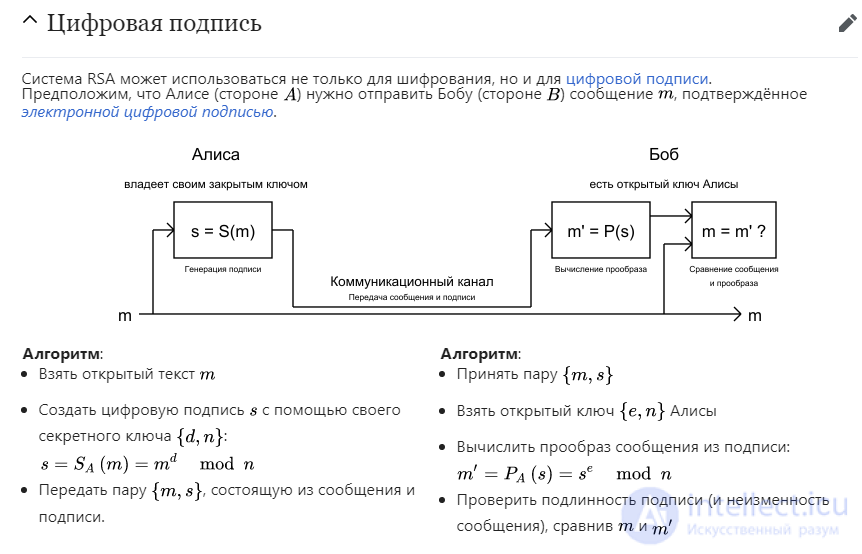
Предположим, Алиса хочет послать Бобу сообщение M , причем таким образом, чтобы Боб был уверен, что сообщение не было взломано и что автором сообщения действительно является Алиса. Алиса создает цифровую подпись S возводя M в степень d и умножая на модуль n:
S = M**d*(mod n), где d и n – частный ключ Алисы. Она посылает M и S Бобу.
Чтобы проверить подпись, Боб возводит S в степень e и умножает на модуль n: M = S**e*(mod n), где e и n – открытый (public) ключ Алисы. Таким образом шифрование и установление подлинности автора сообщения осуществляется без передачи секретных (private) ключей: оба корреспондента используют только открытый (public) ключ своего корреспондента или собственный частный (private) ключ. Послать зашифрованное сообщение и проверить подписанное сообщение может любой, но расшифровать или подписать сообщение может только владелец соответствующего частного (private) ключа.
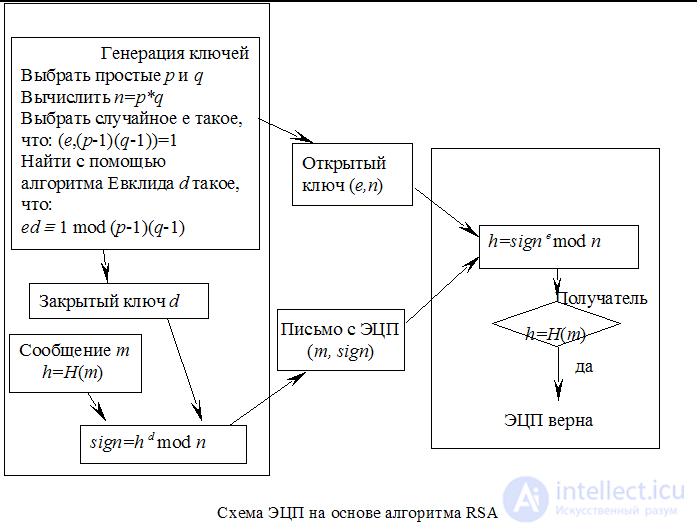
Скорость работы алгоритма RSA
Как при шифровании и расшифровывании, так и при создании и проверке подписи алгоритм RSA по существу состоит из возведения в степень, которое выполняется как ряд умножений. В практических приложениях для открытого ключа обычно выбирается относительно небольшой показатель, а зачастую группы пользователей используют один и тот же открытый показатель, но каждый с различным модулем. Если открытый показатель неизменен, то вводятся некоторые ограничения на главные сомножители (факторы) модуля. При этом шифрование данных идет быстрее расшифровывания, а проверка подписи быстрее, чем подписание.
сли k — количество битов в модуле, то в обычно используемых для RSA алгоритмах количество шагов, необходимых для выполнения операции с открытым ключом, пропорционально второй степени k, количество шагов для операций частного ключа — третьей степени k, количество шагов для операции создания ключей — четвертой степени k.
Методы “быстрого умножения” (например, методы, основанные на быстром преобразовании Фурье (Fast Fourier Transform, FFT)) выполняются гораздо меньшим количеством шагов. Тем не менее, они не получили широкого распространения из-за сложности программной реализации, а также потому, что с распространенными размерами ключей они фактически работают медленнее. Однако производительность и эффективность приложений и оборудования, реализующих алгоритм RSA, быстро увеличиваются. Алгоритм RSA намного медленнее, чем DES и другие алгоритмы блочного шифрования. Программная реализация DES работает быстрее, по крайней мере, в 100 раз и от 1000 до 10 000 — в аппаратной реализации (в зависимости от конкретного устройства). Благодаря ведущимся разработкам, скорость алгоритма RSA, вероятно, увеличится, но одновременно ускорится и работа алгоритмов блочного шифрования.
Алгоритмические задачи, связанные со схемой RSA.
В связи со схемой RSA возникает ряд алгоритмических задач.
1. Для генерации ключей нам надо уметь генерировать большие простые числа. Близкой задачей является проверка простоты целого числа.
2. Для взламывания ключа в RSA нужно уметь раскладывать целое число на множители (или, что практически то же самое, уметь вычислять функцию Эйлера). Взлом ключа может интересовать только преступников, но, с другой стороны, те, кто пытаются защитить информацию, должны быть уверены, что задача разложения на множители достаточно сложна.
Применение алгоритма RSA на практике
На практике криптосистема RSA часто используется вместе с криптографической системой секретного ключа типа DES для зашифровывания сообщения ключом RSA посредством цифрового конверта.
Предположим, что Алиса посылает зашифрованное сообщение Бобу. Сначала она шифрует сообщение по алгоритму DES, используя случайно выбранный ключ DES и затем шифрует ключ DES открытым (public) ключом RSA Боба. Сообщение зашифрованное ключом DES и ключ DES зашифрованный в свою очередь ключом RSA вместе формируют цифровой конверт RSA и отсылаются Бобу. Получив цифровой конверт, Боб расшифровывает ключ DES с помощью своего частного (private) ключа, а затем использует ключ DES, чтобы расшифровать само сообщение.
Применение алгоритма RSA для установления подлинности и цифровых подписей
Криптосистема RSA может использоваться также и для подтверждения подлинности или идентификации другого человека или юридического лица. Это возможно потому, что каждый зарегистрированный пользователь криптосистемы имеет свой уникальный частный (private) ключ, который (теоретически) больше никому недоступен. Именно это делает возможным положительную и уникальную идентификацию Предположим, Алиса желает послать подписанное сообщение Бобу. Она хеширует сообщение (применяет к сообщению хеш-функцию), чтобы создать дайджест сообщения, который является как бы “цифровым отпечатком” сообщения. Затем Алиса шифрует дайджест сообщения своим частным (private) ключом, создавая цифровую подпись, которую посылает Бобу непосредственно вместе с сообщением.
Получив сообщение и подпись, Боб расшифровывает подпись открытым (public) ключом Алисы и получает таким образом даджест сообщения. Затем он обрабатывает сообщение той же хеш-функцией что и Алиса и сравнивает результат с дайджестом сообщения, полученным при расшифровке подписи. Если они совпадают точно, то это означает успешную проверку подписи и Боб может быть уверен, что сообщение действительно послано Алисой. Если же результаты не одинаковы, то это означает, что либо сообщение пришло не от Алисы, либо было изменено при передаче (то есть после того, как Алиса его подписала). Подпись Алисы может проверить любой, кто получил или перехватил это сообщение. Еcли же Алиса хочет сохранить содержание документа в тайне, то она подписывает документ, а затем зашифровывает его открытым (public) ключом Боба. Боб расшифровывает сообщение своим частным (private) ключом и проверяет подпись на восстановленном сообщении, используя открытый (public) ключ Алисы. Либо – если, например, необходимо, чтобы посредник мог подтвердить целостность сообщения, не получая доступ к его содерданию – вместо дайджеста открытого текста может быть рассчитан дайджест зашифрованного сообщения. На практике же общий показатель алгоритма RSA обычно много меньше показателя частного и потому проверка подписи осуществляется быстрее чем подписание. Это является оптимальным так как сообщение подписывется только однажды, а проверка подписи может быть неоднократной.
Для обеспечения секретности обмена информацией необходимо исключить для нападающего возможность во-первых получить открытое сообщение, соответствующее хешированному, а во-вторых получить два различных хешированных сообщения, имеющих одно значение так как в любом из этих случаев нападающий имеет возможность присоединить к подписи Алисы ложное сообщение. Специально для этого разработаны функции хеширования MD5 и SHA, которые делают такое сопоставление невозможным. Цифровая подпись может сопровождаться одним или несколькими сертификатами. Сертификат – заверенный подписью документ, подтверждающий принадлежность открытого (public) ключа определенному владельцу, благодаря чему предотвращается возможность имитации отправителя. Об этом говорит сайт https://intellect.icu . При наличии сертификата, получатель (или третье лицо) имеет возможность удостовериться в принадлежности ключа автору сообщения, то есть ключ позволяет удостоверить сам себя.
Использование криптосистемы RSA в настоящее время
Криптосистема RSA используется в самых различных продуктах, на различных платформах и во многих отраслях. В настоящее время криптосистема RSA встраивается во многие коммерческие продукты, число которых постоянно увеличивается. Также ее используют операционные системы Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм применяется в защищенных телефонах, на сетевых платах Ethernet, на смарт-картах, широко используется в криптографическом оборудовании. Кроме того, алгоритм входит в состав всех основных протоколов для защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, а также используется во многих учреждениях, например, в правительственных службах, в большинстве корпораций, в государственных лабораториях и университетах. На осень 2000 года технологии с применением алгоритма RSA были лицензированы более чем 700 компаниями.
Технологию шифрования RSA BSAFE используют около 500 миллионов пользователей всего мира. Так как в большинстве случаев при этом используется алгоритм RSA, то его можно считать наиболее распространенной криптосистемой общего (public) ключа в мире и это количество имеет явную тенденцию к увеличению по мере роста Internet.
Стандарты с применением RSA
Криптосистема RSA – часть многих стандартов. Стандарт ISO 9796 описывает RSA как совместимый криптографический алгоритм, соотвествующий стандарту безопасности ITU-T X.509. Кроме этого криптосистема RSA является частью стандартов SWIFT, ANSI X9.31 rDSA и проекта стандарта X9.44 для американских банков. Австралийский стандарт управления ключами AS2805.6.5.3 также включает систему RSA. Алгоритм RSA используется в Internet, в частности он входит в такие протоколы как S/MIME, IPSEC (Internet Protocol Security) и TLS (которым предполагается заменить SSL), а также в стандарт PKCS, применяемый в важных приложениях.
Для разработчиков приложений с применением PKCS организация OSI Implementers' Workshop (OIW) выпустила соглашение, которое в частности посвящено алгоритму RSA.
Множество других разрабатываемых в настоящее время стандартов включают в себя либо сам алгоритм RSA или его поддержку либо рекомендуют криптосистему RSA для обеспечения секретности и/или установления подлинности (аутентификации). Например, включают в себя систему RSA рекомендации IEEE P1363 и WAP WTLS.
Криптосистема RSA в мире
На начало 2001 года криптосистема RSA являлась наиболее широко используемой асимметричной криптосистемой (криптосистемой открытого (public) ключа) и зачастую называется стандартом де факто. Вне зависимости от официальных стандартов существование такого стандарта чрезвычайно важно для развития электронной коммерции и вообще экономики. Единая система открытого (public) ключа допускает обмен документами с электронно-цифровыми подписями между пользователями различных государств, использующими различное программное обеспечение на различных платформах; такая возможность насущно необходима для развития электронной коммерции. Распространение системы RSA дошло до такой степени, что ее учитывают при создании новых стандартов. При разработке стандартов цифровых подписей, в первую очередь в 1997 был разработан стандарт ANSI X9.30, поддерживающий Digital Signature Standard (стандарт Цифровой подписи). Годом позже был введен ANSI X9.31, в котором сделан акцент на цифровых подписях RSA, что отвечает фактически сложившейся ситуации в частности для финансовых учреждений.
Недостатки защищенной аутентификации (установления подлинности) были главным препятствием для замены бумажного документооборота электронным; почти везде контракты, чеки, официальные письма, юридические документы все еще выполняются на бумаге. Именно это – необходимость элементов бумажного документооборота – не позволяло полностью перейти к электронным транзакциям. Предлагаемая RSA цифровая подпись – инструмент, который позволит перевести наиболее существенные бумажные документо-потоки в электронно-цифровой вид. Благодаря цифровым подписям многие документы – паспорта, избирательные бюллетени, завещания, договора аренды – теперь могут существовать в электронной форме, а любая бумажная версия будет в этом случае только копией электронного оригинала. Все это стало возможным благодаря стандарту цифровых подписей RSA.
В отличие от симметричного кодирования, при котором процедура расшифровки легко восстанавливается по процедуре шифрования и обратно, в схеме кодирования с открытым ключом невозможно вычислить процедуру расшифровки, зная процедуру шифрования. Более точно, время работы алгоритма, вычисляющего процедуру расшифровки, настолько велико, что его нельзя выполнить на любых современных компьютерах, равно как и на любых компьютерах будущего. Такие схемы кодирования называют асимметричными.
Итак, имеем два отображения:
E: S --> T
D: T --> S
где S -- множество всевозможных незашифрованных сообщений, T -- множество зашифрованных сообщений. Буква "E" -- первая буква слова "Encoding", буква "D" -- первая буква слова "Decoding". Отображение
E: s |--> t
переводит исходное сообщение s в зашифрованное сообщение t, отображение
D: t |--> s
переводит зашифрованное сообщение t обратно в s. Тот факт, что D является декодирующей процедурой, на математическом языке означает, что композиция отображений DE является тождественным отображением: для всякого s справедливо
D(E(s)) = s.
или
DE = 1 (тождественное отображение в S).
Все это справедливо для любой схемы асимметричного кодирования. Перейдем непосредственно к схеме RSA, названной так по первым буквам фамилий ее авторов -- Rumley, Shamir, Adleman. Отметим сразу, что схема RSA обладает двумя дополнительными очень полезными свойствами.
1. Множество исходных сообщений S совпадает с множеством закодированных сообщений T; в качестве этого множества используется кольцо вычетов по модулю m, где m -- произведение двух больших простых чисел (десятичная запись m имеет длину не меньше 200).
2. Не только DE = 1, но и ED = 1! Таким образом, D и E -- два взаимно обратных отображения. Это позволяет владельцу секретной процедуры декодирования D применять ее для кодирования. При этом все могут раскодировать это сообщение, используя открытую процедуру E, но только владелец секретной процедуры D может послать его. Такая "обратная" схема применения открытого ключа позволяет удостоверить отправителя сообщения. В практических применениях (для аутентификации отправителя) обратная схема даже более важна, чем прямая.
Итак, в схеме RSA в качестве множества исходных и зашифрованных сообщений используется кольцо вычетов Zm, где
m = p * q --
произведение двух больших простых чисел (длина десятичной записи каждого из чисел p и q не меньше 100). Всякое сообщение представляется в виде элемента Zm. (Любое собщение -- это последовательность битов, которую можно рассмотреть как большое целое число. Если длина сообщения больше, чем длина двоичной записи m, то оно разбивается на блоки, и каждый блок шифруется отдельно.)
Число m открытое, однако разложение m на множители -- секретное. Разложение позволяет вычислить функцию Эйлера (следствие 3):
phi(m) = (p - 1) * (q - 1)
Нетрудно показать, что знание функции Эйлера дает возможность разложить число на множители, так что сложность задачи взламывания открытого ключа равна сложности задачи разложения на множители. Математики верят, что это действительно сложная задача, хотя никаких удовлетворительных оценок снизу в настоящее время не получено. (И вряд ли это NP-полная задача.)
Построение кодирующей процедуры E
Сгенерируем случайный элемент e в кольце вычетов по модулю phi(m), такой, что он обратим в этом кольце (т.е. взаимно прост с phi(m)). Пара (m, e) является открытым ключом. Отображение E состоит в возведении в степень e в кольце вычетов по модулю m.
E: s |--> s^e (mod m)
Для практического вычисления применяется алгоритм быстрого возведения в степень.
Построение декодирующей процедуры D.
Для элемента e вычисляется обратный элемент d в кольце вычетов по модулю phi(m).
e * d == 1 (mod phi(m))
Это легко делается с помощью расширенного алгоритма Евклида. Пара (m, d) является секретным ключом. Отображение D состоит в возведении в степень d в кольце вычетов по модулю m.
D: t |--> t^d (mod m)
Покажем, что отображение D является левым обратным к E, т.е. для всякого ссобщения s выполняется равенство D(E(s)) = s. Имеем
D(E(s)) == D(s^e) == (s^e)^d == s^(e*d) (mod m)
Так как e*d == 1 (mod phi(m)), имеем
e*d = 1 + h * phi(m)
По следствию 4,
s^(e*d) = s^(1 + h*phi(m)) == s (mod m)
Итак, DE = 1. Аналогично доказывается, что ED = 1.
Суммируем все вышесказанное.
Рассматривается множество сообщений Zm, где m -- произведение двух больших простых чисел: m = p*q. Число m является открытым, но его разложение на множители -- секретным. Знание разложения позволяет вычислить функцию Эйлера phi(m) = (p-1)*(q-1). Случайным образом выбирается обратимый элемент e в кольце вычетов по модулю phi(m). Для него вычисляется (с помощью расширенного алгоритма Евклида) обратный элемент d в кольце вычетов по модулю phi(m). Отображение E задается парой (m, e) и состоит в возведении в степень e по модулю m:
E(s) = s^e (mod m).
Отображение D задается парой (m, d) и состоит в возведении в степень d по модулю m:
D(t) = t^d (mod m).
Эти два отображения взаимно обратны. Пара (m, e) является открытым ключом (public key), пара (m, d) является секретным ключом (private key).
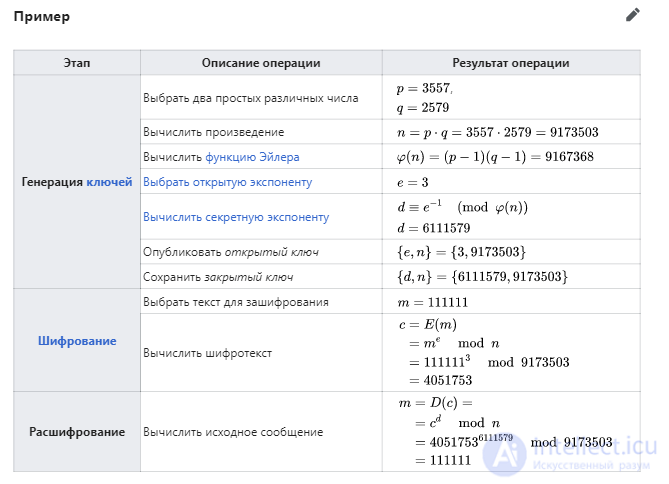
Пример. Рассмотрим пример с небольшими числами, чтобы только проиллюстрировать схему RSA. В реальных приложениях используют большие целые числа, порядка 200-400 десятичных цифр.
Пусть m = 11*13 = 143. Вычислим функцию Эйлера phi(m) = 10*12 = 120. Выберем e = 113, тогда d = 17 -- обратный к e элемент в кольце Z120.
Действительно,
113 * 17 = 1921 = 120 * 16 + 1.
Пара (143, 113) составляет открытый ключ, пара (143, 17) -- секретный ключ. Отображение E состоит в возведении в степень 113 по модулю 143, отображение D -- в степень 17 по модулю 143. Рассмотрим произвольное сообщение s = 123. Тогда
E(123) == 123^113 (mod 143) == 41.
Таким образом, 41 -- это закодированное сообщение. Применим к нему декодирующую процедуру:
D(41) == 41^17 (mod 143) == 123.
Мы получили исходное сообщение.
Вокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает.
Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах.
Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надежности канала передачи данных. Приступим.
Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.
Теперь пара чисел {e, n} — это мой открытый ключ. Я отправляю его вам, чтобы вы зашифровали свое сообщение. Но для меня это еще не все. Я должен получить закрытый ключ.
Мне нужно вычислить число d, обратное е по модулю φ. То есть остаток от деления по модулю φ произведения d×e должен быть равен 1. Запишем это в обозначениях, принятых во многих языках программирования: (d×е)%φ=1. Или (d×5)%12=1. d может быть равно 5 ((5×5)%12=25%12=1), но чтобы оно не путалось с e в дальнейшем повествовании, давайте возьмем его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 (17×5-12×7=1). Итак d=17. Пара {d, n} — это секретный ключ, его я оставляю у себя. Его нельзя сообщать никому. Только обладатель секретного ключа может расшифровать то, что было зашифровано открытым ключом.
Теперь пришла ваша очередь шифровать ваше сообщение. Допустим, ваше сообщение это число 19. Обозначим его P=19. Кроме него у вас уже есть мой открытый ключ: {e, n} = {5, 21}. Шифрование выполняется по следующему алгоритму:
Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.
Полученные данные E=10, вы отправляете мне.
Здесь надо заметить, что сообщение P=19 не должно быть больше n=21. иначе ничего не получится.
Я получил ваши данные (E=10), и у меня имеется закрытый ключ {d, n} = {17, 21}.
Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.
Начинаем раскодировать:
Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение (E=10), так как ни у кого нет закрытого ключа.
Надежность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел (p и q). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля n на простые сомножители p и q. Если число является произведением двух очень больших простых чисел, то его очень трудно разложить на множители.
Постараюсь это показать на примере. Давайте разложим на множители число 360:
Мы на каждом шагу, практически без перебора, получали все новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5
Давайте теперь возьмем число 361. Тут нам придется помучиться.
При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время.
Многие читатели спрашивают, как все это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.
Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.
Оттолкнемся от пары простых чисел {p, q} = {17, 19}. Пусть наш открытый ключ будет {e, n} = {5, 323}, а закрытый {d, n} = {173, 323}.
Мы готовы к шифрованию. Переведем наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19.
Мы можем зашифровать каждое из этих чисел открытым ключом {e, n} = {5, 323} и получить шифровку 197, 272, 2, 304. Эти числа можно передать получателю, обладающему закрытым ключом {d, n} = {173, 323} и он все расшифрует.
На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путем недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.
Таким образом, злоумышленнику не придется отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.
Упрощенно, это выглядит так. Перед шифрованием, мы применяем к сообщению правило: b := (b + a) % n. Где a — предыдущая часть сообщения, а b — следующая. То есть наше сообщение (11, 17, 15, 19) изменяется. 11 остается без изменений. 17 превращается в (11 + 17) % 323 = 28. 15 становится (15 + 28) % 323 = 43. A 19 превращается в 62.
Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.
Тот, кто получит ваше сообщение, должен будет проделать обратную операцию, со знаком «минус»: b := (b - a) % n. И только тогда он получит коды букв.
На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения.
То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.
В реальной жизни все еще немного сложнее. Блоки, на которые бьется сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование.
Получатель делает все в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков).
Для элемента e вычисляется обратный элемент d в кольце вычетов по модулю phi(m).
e * d == 1 (mod phi(m))
Это легко делается с помощью расширенного алгоритма Евклида. Пара (m, d) является секретным ключом. Отображение D состоит в возведении в степень d в кольце вычетов по модулю m.
D: t |--> t^d (mod m)
Покажем, что отображение D является левым обратным к E, т.е. для всякого ссобщения s выполняется равенство D(E(s)) = s. Имеем
D(E(s)) == D(s^e) == (s^e)^d == s^(e*d) (mod m)
Так как e*d == 1 (mod phi(m)), имеем
e*d = 1 + h * phi(m)
По следствию 4,
s^(e*d) = s^(1 + h*phi(m)) == s (mod m)
Итак, DE = 1. Аналогично доказывается, что ED = 1.
Суммируем все вышесказанное.
Рассматривается множество сообщений Zm, где m -- произведение двух больших простых чисел: m = p*q. Число m является открытым, но его разложение на множители -- секретным. Знание разложения позволяет вычислить функцию Эйлера phi(m) = (p-1)*(q-1). Случайным образом выбирается обратимый элемент e в кольце вычетов по модулю phi(m). Для него вычисляется (с помощью расширенного алгоритма Евклида) обратный элемент d в кольце вычетов по модулю phi(m). Отображение E задается парой (m, e) и состоит в возведении в степень e по модулю m:
E(s) = s^e (mod m).
Отображение D задается парой (m, d) и состоит в возведении в степень d по модулю m:
D(t) = t^d (mod m).
Эти два отображения взаимно обратны. Пара (m, e) является открытым ключом (public key), пара (m, d) является секретным ключом (private key).
Пример. Рассмотрим пример с небольшими числами, чтобы только проиллюстрировать схему RSA. В реальных приложениях используют большие целые числа, порядка 200-400 десятичных цифр.
Пусть m = 11*13 = 143. Вычислим функцию Эйлера phi(m) = 10*12 = 120. Выберем e = 113, тогда d = 17 -- обратный к e элемент в кольце Z120.
Действительно,
113 * 17 = 1921 = 120 * 16 + 1.
Пара (143, 113) составляет открытый ключ, пара (143, 17) -- секретный ключ. Отображение E состоит в возведении в степень 113 по модулю 143, отображение D -- в степень 17 по модулю 143. Рассмотрим произвольное сообщение s = 123. Тогда
E(123) == 123^113 (mod 143) == 41.
Таким образом, 41 -- это закодированное сообщение. Применим к нему декодирующую процедуру:
D(41) == 41^17 (mod 143) == 123.
Мы получили исходное сообщение.
Выводы из данной статьи про криптосис rsa цифровая подпись указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое криптосис rsa цифровая подпись и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Шифры в криптографии
Комментарии
Оставить комментарий
Информационная безопасность, Шифры в криптографии
Термины: Информационная безопасность, Шифры в криптографии