Лекция
Привет, Вы узнаете о том , что такое медовое шифрование , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое медовое шифрование , настоятельно рекомендую прочитать все из категории Шифры в криптографии.
медовое шифрование — тип симметричного шифрования, при котором шифротекст расшифровывается с любым допустимым ключом в правдоподобный открытый текст .
В 1999 году Даглас Хувер и Нат Каузик рассмотрели проблему защиты закрытого ключа в криптосистемах с открытым ключом, в частности, секретной экспоненты в RSA и секретного ключа в DSA и предложили алгоритм маскировки этой секретной компоненты с помощью пароля (шести-восьмибитной строки). В своей работе они утверждали, что для таких паролей перебор по словарю будет давать результат такой же структуры, что и защищаемый закрытый ключ, и злоумышленник не сможет различить правильно расшифрованные данные от многих других правдоподобных, но ложных расшифровок, пока не попытается использовать полученные ключи для доступа к взламываемому ресурсу через сервер аутентификации. Сервер обнаружит несколько ошибок аутентификации и приостановит доступ. Такой подход обеспечивает дополнительную меру безопасности, что дает возможность, например, уменьшить размерность пространства ключей .
В последующем были предложены системы хранения паролей, использующие схожий метод маскировки сохраненных аутентификационных данных среди списка явно поддельных, для предотвращения рассекречивания базы данных в случае, к примеру, утечки хеш-файла паролей.
Основываясь на подобных системах маскировки, Ари Джулз из Корнеллского Университета и Томас Ристенпарт из Университета Висконсина представили доклад о медовом шифровании на конференции Eurocrypt[en] 2014 .
В начале 2014 года американские ученые Ари Джулс и Томас Ристенпарт выдвинули новую идею в криптографии, которая потенциально может иметь заметное практическое приложение. Эта идея носит название «медовое шифрование» («honey encryption») и заключается в таком шифровании, которое при неверно введенном ключе выдает ложные, но правдоподобно выглядящие данные. В своей работе они приводят леммы и теоремы, доказывающие, что предлагаемая ими идея с математической точки зрения вполне имеет право на жизнь.
Медовое шифрование предназначено для защиты от атак, использующих метод полного перебора. Подобные атаки представляют собой взлом путем перебора всех возможных вариантов ключа, что эквивалентно выбору случайных открытых текстов из пространства всех возможных открытых текстов с дискретным равномерным распределением. Это может быть эффективным: несмотря на то что злоумышленник с равной вероятностью получает любой возможный открытый текст, большинство из них крайне неправдоподобны, другими словами, распределение разумных открытых текстов неравномерно. Механизм защиты медового метода основывается на преобразовании пространства открытых текстов в такое пространство, что распределение правдоподобных открытых текстов в нем равномерно. Таким образом, угадывающий ключи злоумышленник будет часто получать разумно выглядящие тексты, а случайно выглядящие тексты редко. Это затрудняет понимание, был ли угадан правильный ключ. В сущности, медовое шифрование выдает ложные данные в ответ на каждое неверное предположение о пароле или ключе шифрования .
Безопасность медового шифрования основана на том, что вероятность того, что злоумышленник сочтет открытый текст верным, может быть рассчитана (шифрующей стороной) во время шифрования. Это затрудняет применение медового шифрования в определенных приложениях, где пространство открытых текстов очень велико или их распределение неизвестно. Также это означает, что медовое шифрование может быть уязвимо для атак методом «грубой силы», если эта вероятность будет неправильно посчитана. Например, он уязвим для атак на основе открытых текстов, если у злоумышленника есть «шпаргалка», это значит, что он обладает определенным числом открытых текстов и соответствующих им шифротекстов, это делает возможным перебор даже данных, зашифрованных медовым методом, если ее наличие не было учтено при зашифровке .
К недостаткам алгоритма относится проблема опечаток: если доверенный пользователь ошибется при наборе ключа, то он получит поддельный открытый текст, выглядящий при этом правдоподобно, и у него не будет возможности понять это. Также актуален вопрос создания семантически и контекстно корректного ложного сообщения, которого будет достаточно, чтобы обмануть злоумышленника. Сгенерированные сообщения должны быть трудно отличимы от реальных сообщений, при этом они должны следовать правилам и нормам языка и в то же время скрывать значимую информацию из оригинального текста .
При распространенном сегодня подходе полный перебор всех ключей шифрования обязательно дает результат. Даже если не используются имитовставки, электронные подписи или дополнения при шифровании, говорящие о правильности или неправильности расшифровки, при использовании неверного ключа осмысленные данные расшифровываются в последовательность псевдослучайных чисел, часто легко отличимых от реальных данных компьютером или человеком. Длина ключей многих алгоритмов такова, что провести полный перебор просто невозможно, однако нередко из-за проблем криптографического алгоритма или его реализации можно заменить полный перебор сокращенным, сильно ускорив процесс . Сокращенный перебор по словарю показан на рис. 1.

Рис. 1. Процесс подбора пароля путем перебора по словарю (на основе )
В своей статье ученые предлагают подход, при котором не только частичный, но даже полный перебор всех возможных ключей может оказаться бесполезным за счет хитрого трюка: при использовании любого ключа (правильного или неправильного) для расшифрования данных всегда получается правдоподобный результат, и из-за этого крайне сложно отличить правильно расшифрованные данные от подложных (рис. 2). Это может быть очень полезно в системах, где трудно обеспечить стойкое шифрование, например при генерации ключа шифрования из пароля, а также во многих других приложениях.
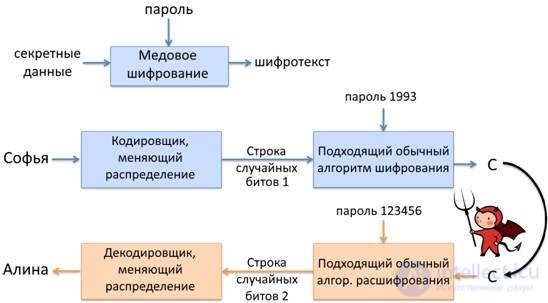
Рис. 2. Схема медового шифрования (на основе )
Как и любая другая концепция, медовое шифрование опирается на некоторые предположения. В данном случае важным предположением является то, что при расшифровке шифротекста неверным ключом мы получаем псевдослучайные данные, и именно из-за этого мы можем отсечь множество результатов дешифрования как неправдоподобные. В разделе 2 данной работы это предположение будет подвергнуто проверке при использовании алгоритма шифрования RSA . Помимо этого, в разделе 1 будут рассмотрены вопросы совместного применения медового шифрования и алгоритма RSA в целом, без привязки к конкретным типам данных.
В медовом шифровании участвуют три набора: набор всех сообщений (пространство сообщений), набор всех ключей
(пространство ключей) и набор так называемых промежуточных значений
(от англ. Seed). Также важной частью медового шифрования является кодер преобразования с распределением или DTE (от англ. Distribution Transforming Encoder), состоящий из двух алгоритмов кодирования и декодирования, устанавливающих связь между пространствами
и
. При кодировании обычный текст сопоставляется с промежуточным значением с помощью DTE, а затем преобразуется в зашифрованный текст с использованием какого-либо симметричного метода шифрования c выбранным ключом. Процедура декодирования с ключом возвращает промежуточное значение, которое затем транслируется DTE в правильное сообщение .
Сообщение может быть сопоставлено нескольким промежуточным значениям, но каждое значение — только одному сообщению. Если для сообщения возможно несколько значений, в алгоритме кодирования случайно выбирается ровно одно. Таким образом, этот алгоритм кодирования рандомизирован, а алгоритм декодирования детерминирован. Количество значений, которые сопоставляются сообщению, должно быть пропорционально его вероятности. Таким образом, для создания DTE должно быть известно дискретное распределение вероятности появления сообщений[10].
При неправильном ключе зашифрованный текст сопоставляется с другим значением и, таким образом, расшифровывается в ложное сообщение .
Конкретная практическая реализация схемы медового шифрования может быть устроена, например, следующим образом. Все сообщения в сортируются в некотором порядке, затем вычисляются вероятность
и функция распределения
каждого сообщения. Об этом говорит сайт https://intellect.icu . Далее DTE сопоставляет открытое текстовое сообщение с диапазоном значений из
, причем начало диапазона определяется функцией распределения, а конец — вероятностью данного сообщения. После чего DTE случайным образом выбирает элемент из этого диапазона, который затем шифруют по подходящей схеме симметричного шифрования с использованием ключа
для получения шифротекста. Процедура дешифрования производится, соответственно, по той же схеме и с тем же
. Затем DTE определяет местоположение полученного значения
, оно соответствует значению вероятности, которое лежит между функцией распределения искомого сообщения и следующего за ним в пространстве
. Посредством поиска по таблице соответствий сообщения и его
DTE восстановит исходное текстовое сообщение[11].
11 — это шифротекст. Во время дешифрования зашифрованный текст повторно складывается по модулю 2 с ключом:
Это снова промежуточное значение, которое затем сопоставляется с исходным сообщением DTE. Сообщение снова расшифровано.
Если злоумышленник пробует ключ, например, 00, он складывает зашифрованный текст с этим ключом и получает {\displaystyle 11\oplus 00=11}, который декодируется синим цветом. Злоумышленник не может определить, является ли это сообщение правильным или неправильным[13].
Различные адаптации алгоритма медового шифрования находят свое применение в вопросе защиты данных, находящихся в облачных хранилищах, как пример реализация[14] дополнительной защиты для зашифрованных файлов, помимо пользовательского пароля. Если злоумышленник пытается получить доступ к зашифрованным данным с помощью перебора вариантов пароля методом «грубой силы», вместо того, чтобы запрещать доступ, алгоритм генерирует неразличимый поддельный файл, связанный с исходным файлом. Аналогичная система была предложена для защиты приложений, используемых в интернет-банкинге[15].
На конференции ICASSP[en] 2016 был представлен концепт устойчивого к прослушиванию мессенджера, создающего правдоподобные сообщения при попытке атаковать зашифрованные сообщения[16].
1. О совместном применении медового шифрования и шифрования RSA
В оригинальной работе о медовом шифровании сказано, что совместно с медовым шифрованием могут использоваться не все криптографические примитивы. Во-первых, мы разумеется не должны использовать имитовставки, электронные подписи или дополнения при шифровании, говорящие о правильности или неправильности расшифровки, а во-вторых, используемый алгоритм шифрования должен удовлетворять свойству «шифрование равномерно распределенных открытых текстов дает равномерно распределенные шифротексты». Группа студентов Массачусетского технологического института в своей статье утверждает, что данное условие выполняется для асимметричного алгоритма шифирования RSA. Это известный, хорошо исследованный и стандартизированный асимметричный алгоритм, широко используемый на протяжении нескольких десятилетий.
Для работы с этим алгоритмом будет разумнее всего применить самый популярный продукт в своей области – мощнейшую свободную библиотеку OpenSSL . При использовании этой библиотеки перед нами встает вопрос выбора длины ключа. Длина ключа в 2048 бит сегодня считается относительно безопасной и активно используется при шифровании в протоколе TLS, защищающем большинство зашифрованных соединений в сети Интернет.
Алгоритм RSA обычно не используется для шифрования больших пакетов данных – гораздо более эффективной во всех отношениях (скорость, длина шифротекста, безопасность) является гибридная криптосистема, в которой асимметричный алгоритм (например, RSA) используется для шифрования ключа симметричного алгоритма (например, AES), который и используется собственно для шифрования данных. Алгоритм шифрования RSA накладывает жесткие ограничения на размер открытого текста, который должен быть равен размеру ключа, то есть в случае 2048-битного ключа открытый текст тоже должен быть равен 2048 битам (256 байт). При этом открытый текст, представленный как число, должен быть меньше модуля n = p*q, длина которого (модуля) в битах равна длине ключа, что еще сильнее сужает пространство открытых текстов [10]. Например, открытый текст, состоящий из 2048 единичных бит, не может быть зашифрован без дополнительных ухищрений при использовании 2048-битного ключа. Нам придется учесть все это.
Библиотека OpenSSL предоставляет возможность использования криптографического дополнения при шифровании, что позволяет усилить безопасность алгоритма, а также шифровать данные длиной меньше, чем размер ключа [11]. Более конкретно, OpenSSL позволяет использовать дополнение в соответствии со стандартом PKCS #1 v2.0 (алгоритм EME-OAEP), в соответствии со стандартом PKCS #1 v1.5, модификацию последнего для протокола SSL версий 2 и 3, а также не использовать дополнение вообще [12]. Использование дополнения здесь является не просто правилом хорошего тона, но насущной необходимостью. Перечисленные выше три вида дополнений имеют строгую структуру, которая нарушит свойство «медовости» шифрования — если строго заданные в стандарте байты дополнения будут неверными, то злоумышленник поймет, что текущий результат дешифрования недостоверен. Хорошим решением было бы ввести свое дополнение, максимально подходящее для задачи медового шифрования.
Каким было бы хорошее дополнение в данном случае? Во-первых, хотелось бы избавиться от ситуации, когда число, получающееся из открытого текста, будет больше модуля n. Поскольку модуль n скорее всего имеет единичные старшие биты, которые хранятся в первом байте, то для того, чтобы открытый текст заведомо был меньше модуля, нужно дополнить его слева нулевыми битами. В случае использования OAEP, например, первый байт дополнения равен 0 (0x00), и мы поступим так же. Для нас введение такого байта является вынужденной необходимостью, поскольку из-за него в среднем лишь одна попытка дешифрования из 2^8 = 256 даст правдоподобный результат, но все же стоит сделать это.
Во-вторых, использование RSA без дополнения не является безопасным, в частности из-за возможной атаки на основе адаптивно подобранного шифротекста [13]. После обнуления первого байта мы могли бы осуществить дополнение псевдослучайными байтами со второго байта, причем для борьбы с атакой дней рождений число байт должно быть не менее 32 (таким образом, получаем 256 псевдослучайных бит). Длину реальных данных придется хранить в открытом или зашифрованном виде в другом месте, поскольку хранение его непосредственно в дополнении поможет злоумышленнику отделить правильные попытки расшифровки от неправильных. Итак, минимум 33 из 256 байт нам придется отвести под дополнение, тогда для осмысленных данных нам остается лишь не более 223. Если нам нужно зашифровать меньшее число байт, например, 200, то мы будем использовать 32 + 23 = 55 псевдослучайных байт вместо 32.
Возможно, высказанные выше предположения о том, что нам нужно обнулить не менее 8 первых бит открытого текста, а затем заполнить не менее 32 байт псевдослучайными данными, были слишком параноидальными. В этом случае можно повысить эффективность нашего дополнения — усложнить злоумышленнику задачу отделения реальных данных от ложных и/или шифровать больше полезных данных в одном шифротексте.
Итак, алгоритм RSA допускает совместно с ним использование медового шифрования, однако его применение сильно затруднено и ограничено, вследствие чего гораздо лучшим решением было бы использование гибридной криптосистемы. При внедрении медового шифрования перед шифрованием данных симметричным алгоритмом и после расшифровки данных им же мы получим улучшение удобства использования, усиление безопасности и увеличение скорости, а сам ключ симметричного алгоритма можно без особых проблем зашифровать с помощью того же RSA.
2. Проверка утверждения о результатах расшифровки
Итак, покажем вычислительно, что при расшифровке шифротекста неверным ключом в алгоритме RSA мы получаем псевдослучайные данные, и именно из-за этого мы можем отсечь множество результатов расшифрования как неправдоподобные. Для решения этой задачи была написана программа [18].
Сначала эта программа составляет открытый текст для шифрования. Он состоит из дополнения (обнуленный первый байт, затем 32 псевдослучайных байта) и собственно данных (223 оставшихся байта), его общая длина таким образом составляет 256 байтов. В байтах данных для чистоты эксперимента будут каждый раз лишь одно повторяющееся однобайтовое значение, причем это будут крайние и средние значения из возможного диапазона (0, 1, 50, 100, 150, 200, 255). Именно в случае шифрования этих сильно неравномерных открытых текстов наиболее вероятно проявится неравномерное распределение результатов дешифрования, если оно действительно имеет место быть. Итак, полученное сообщение шифруется только что сгенерированным открытым ключом, затем расшифровывается соответстующим ему закрытым ключом, чтобы подтвердить правильность расшифровки.
После этого мы совершаем атаку на зашифрованный алгоритм, пытаясь расшифровать шифротекст свежесгенерированными секретными ключами. Программная реализация алгоритма RSA является весьма медленной, поскольку RSA – асимметричный алгоритм, так что при моделировании атаки нам придется ограничиться 256 попытками подобрать ключ (сложность атаки – 2^8), а также не брать в расчет значение первого байта (как уже упоминалось, если его значение не нулевое, то результат расшифровки уже неправдоподобен, но мы игнорируем это). В случае, если получившийся расшифрованный текст будет больше модуля (что невозможно при правильной расшифровке), мы подбираем ключ для этой итерации заново. После каждого расшифрования, кроме случая “расшифрованный текст больше модуля“, мы будем собирать статистику по частоте встречаемости различных байт в расшифрованных данных, то есть в последних 223 байтах (дополнение нас не интересует). Для проверки соответствия получившегося и равномерного распределения данных (именно его дали бы идеальные случайные данные) мы будем использовать функцию CHITEST редакторов таблиц Microsoft Excel / OpenOffice alc / LibreOffice Calc, осуществляющую статистическую проверку гипотезы по критерию хи-квадрат [14, 15].
Результаты несколько разнятся от опыта к опыту в силу случайности генерации 32 байт из дополнения, ключа шифрования и ключей дешифрования, но все же качественно, по своей сути они остаются прежними и при повторении опытов. Степень сходства между расшифрованными и псевдослучайными данными при шифровании чисел 0 – 0,24 (в другом тесте – 0,02), чисел 1 – 0,70, чисел 50 – 0,80 (в другом тесте – 0,11), чисел 100 – 0,58, чисел 150 – 0,79, чисел 200 – 0,64, чисел 255 – 0,73 (в другом тесте – 0,10).
Возьмем, пожалуй, худший случай из перечисленных выше – шифрование чисел 0, и проведем для него более длительный опыт – будем пытаться подобрать ключ 8192 раза (в 32 раза больше, чем ранее). Получим, что степень сходства по критерию хи-квадрат равна 0,61, что является еще одним подтверждением нашей гипотезы.
Собрав в этом же опыте отдельную статистику по первым байтам сообщений (в исходном сообщении на этом месте стоял обнуленный байт дополнения), получим очень близкую к нулю степень (9E-320) сходства реального и равномерного распределений, показывающую их сильное отличие. Пристальный взгляд на результаты говорит сам за себя (рис. 3). Первый байт не принял значения в диапазоне [205; 255] ни разу за 8192 итерации, то есть его значение жестко ограничено сверху. По-видимому, подобное ограничение является неотъемлемым свойством алгоритма RSA. Первый байт принял значение 0 всего в 45 из 8192 итераций, то есть злоумышленник, знающий об используемом дополнении, в нашем опыте cмог бы отсечь (8192-45) / 8192 * 100% ~ 99,45% полученных результатов как недостоверные уже на этом шаге. Однако, как мы уже упоминали, в нашей работе мы не учитываем это обстоятельство при сборе статистики. Стоит упомянуть, что в данном опыте мы получаем всего 8192 различных первых байт, и при равномерном распределении каждому возможному значению от 0 до 255 соответствует лишь 32 вхождения, что является весьма небольшим числом для статистики. Увы, проводить более длительные (и, соотвественно, более достоверные) опыты для нас затруднительно.

Рис. 3. Распределение первого байта сообщения. Синим показано реальное распределение, красным – равномерное
Подводя итог, если бы у нас была возможность проводить большее количество объемных опытов за разумные промежутки времени, то возможно мы получили бы большее соответствие. С другой стороны, опыт показывает, что некоторые ключи шифрования вызывают значительно более частое появление ошибки “открытый текст больше модуля” при дешифровании, чем другие: эта ошибка либо не появляется в ходе запуска программы вообще, либо появляется редко, либо появляется часто. Есть предположение, это тоже может влиять на статистические свойства результатов дешифрования.
Таким образом, даже с учетом заметного разброса значений в целом предположение о псевдослучайности расшифрованных неверным ключом данных является в целом верным, что подтверждают диаграммы, построенные на основе полученных данных. Распределение не является строго равномерным, но близко к нему.
3. Наброски для математического рассмотрения вопроса
Разумеется, идеальным было бы доказать равномерность распределения при расшифровке неверным ключом не только вычислительно, но и строго математически. К сожалению, это является очень сложным вопросом, выходящим за компетенцию автора данной работы. Подтверждением сложности является, например, статья французских ученых [16], которые рассматривают значительно более узкие вопросы, и тем не менее сложность оказывается очень высокой.
Тем не менее, хотелось бы представить некоторые наброски, могущие быть полезными для будущих работ по этой теме. Была написана программа [18], с помощью которой можно сделать некоторые выводы о распределении результатов выражения x^y mod p, где y>=2, p и y фиксированы в каждом опыте. Дело в том, что если результаты этого выражения при описанных выше условиях не повторяются для всех x из отрезка [0; p-1], то распределение результатов будет равномерным; напротив, хотя бы одно повторение сделает распределение неравномерным.
Проведем следующий эксперимент: p находится в промежутке [2; 100]; y находится в промежутке [2; 40]; x находится в промежутке [0; p-1], пробегая в каждом опыте все свои возможные значения. Получим следующие результаты:
1. Если p = 2, то при любой степени y из интервала [1; 40] получаем равномерное распределение. Все просто: 0^y mod 2 = 0 при любой степени y>=1, 1^y mod 2 = 1 при любой степени y>=1, так что равномерное распределение здесь будет при любых y>=1.
2. Если p = 3, то при любой нечетной степени y из интервала [1; 40] получаем равномерное распределение. Это объясняется тем, что 0^y mod 3 = 0 при любой степени y>=1, 1^y mod 3 = 1 при любой степени y>=1, а вот 2^y mod 3 = 2 только при нечетных степенях y, так что равномерное распределение здесь будет при любых нечетных y>=1.
3. Если p принимает значение из множества {4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, 32, 36, 40, 44, 45, 48, 49, 50, 52, 54, 56, 60, 63, 64, 68, 72, 75, 76, 80, 81, 84, 88, 90, 92, 96, 98, 99, 100}, то даже при любом y из отрезка [2; 500] равномерное распределение не встречается ни разу. Легко заметить закономерность – все эти числа кратны как минимум одному из следующих чисел: 4 (2^2), 9 (3^2), 25 (5^2) и 49 (7^2), то есть квадратам простых чисел. Судя по всему, эта закономерность соблюдается и далее.
4. Если p не удовлетворяет описанному выше условию кратности квадратам простых чисел, то для него обязательно существует множество нечетных значений y, при которых распределение будет равномерным. Например, если p = 29, то в нашем опыте y может принадлежать множеству {1, 3, 5, 9, 11, 13, 15, 17, 19, 23, 25, 27, 29, 31, 33, 37, 39}. Здесь можно увидеть закономерность, если мы найдем разности между соседними членами: 3-1 = 2, 5-3 = 2, 9-5 = 4, 11-9 = 2, 13-11 = 2, 15-13 = 2, 17-15 = 2, 19-17 = 2, 23-19 = 4, 25-23 = 2, 27-25 = 2, 29-27 = 2, 31-29 = 2, 33-31 = 2, 37-33 = 4, 39-37 = 2. Сначала разница два раза равна 2, затем равна 4; затем пять раз равна 2, затем равна 4; затем пять раз равна 2, затем равна 4. Аналогичным образом ситуация обстоит и с другими подходящими p – для них y также может принадлежать множеству значений, которые связаны между собой каким-то законом. Судя по всему, упомянутые выше закономерности соблюдается и далее.
В алгоритме RSA при расшифровке роль модуля p из построений выше играет число n = p*q, где p и q – простые числа; роль степени y играет секретная экспонента d, а роль x играет шифротекст x из интервала [0; n-1]. В стандарте RSA сказано, что p !=q: «In a valid RSA public key, the RSA modulus n is a product of u distinct odd primes». Отсюда прямо вытекает, что мы имеем дело с ситуацией 4, рассмотренной выше (раз модуль равен произведению различных простых чисел, то он не может быть кратен квадрату какого-либо простого числа). Поскольку d = e^(-1) mod ф(n) = e^(-1) mod (p-1)*(q-1), то скорее всего d может быть любым числом (вообще-то это требует дополнительного исследования!), и соответственно распределение результатов расшифровки одним ключом различных сообщений может быть как равномерным, так и неравномерным (соответственно в общем случае оно будет неравномерным).
Нас, однако, куда больше интересует распределение результатов расшифровки одного сообщения различными ключами: хотелось бы рассмотреть ситуацию, когда в выражении x^y mod p значение y меняется в диапазоне [0; p-1], а x и p остаются постоянными на протяжении каждого опыта. Переработав для этой цели ранее описанную программу [18] и рассматривая числа в отрезке [2; 50], мы обнаружим, что в ряде случаев (но далеко не всегда!) распределение действительно будет очень близким к равномерному. В тех случаях, когда p является простым числом (в наших опытах это были числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47), при некоторых значениях x результат выражения будет равномерно распределен между значениями [1; p-1] при степенях y в интервале [0; p-2]. Другими словами, в этих случаях при степенях y в интервале [0; p-2] результат никогда не принимает нулевого значения, зато принимает все другие возможные значения лишь однажды, так что распределение будет практически равномерным. Закономерности в подходящих значениях x тут найти не удалось: например, при p = 23 подходящие x принадлежат множеству {5, 7, 10, 11, 14, 15, 17, 19, 20, 21}. Можно лишь сказать, что их сравнительно немало — в нашем эксперименте от четверти до половины всех возможных значений x. Стоит отметить, что не стоит считать такие числа x первообразными корнями по модулю p [17], поскольку в общем случае они ими не являются.
Однако в алгоритме RSA в качестве модулей используются полупростые числа (произведения двух простых чисел), а не простые, так что судя по нашим опытам такие благоприятные ситуации возникать не будут, а значит строго говоря распределение нельзя будет назвать равномерным.
Исследование, описанное в статье про медовое шифрование , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое медовое шифрование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Шифры в криптографии
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Информационная безопасность, Шифры в криптографии
Термины: Информационная безопасность, Шифры в криптографии