Эллиптическая криптография, Эллиптические кривые сущность, достоинства и недостатки

Привет, Вы узнаете о том , что такое эллиптическая криптография, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое эллиптическая криптография, эллиптические кривые , настоятельно рекомендую прочитать все из категории Шифры в криптографии.

эллиптические кривые

эллиптическая криптография - это метод криптографии, основанный на математических свойствах эллиптических кривых. Этот подход к криптографии обеспечивает высокий уровень безопасности при более коротких ключах, чем используются в классической криптографии.

Эллиптическая кривая представляет собой множество точек (x, y), удовлетворяющих уравнению:

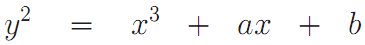
где a и b - коэффициенты кривой. Она имеет различные свойства, которые делают ее полезной в криптографии:

1. Сложение точек: Для двух точек на эллиптической кривой можно определить операцию сложения, которая позволяет находить третью точку на кривой, лежащую на прямой, проходящей через две заданные точки. Это обеспечивает основу для операций шифрования и цифровой подписи.

2. Дискретный логарифм: В эллиптической криптографии безопасность основана на сложности вычисления дискретного логарифма. Это означает, что даже если злоумышленник знает общедоступный ключ (точку на эллиптической кривой), ему трудно вычислить значение приватного ключа (целое число), используемого для шифрования или подписи.

Эллиптическая кривая — это набор точек, описывающихся уравнением Вейерштрассе:

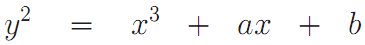
Типичные варианты графиков эллиптических кривых вы сможете посмотреть под спойлером:

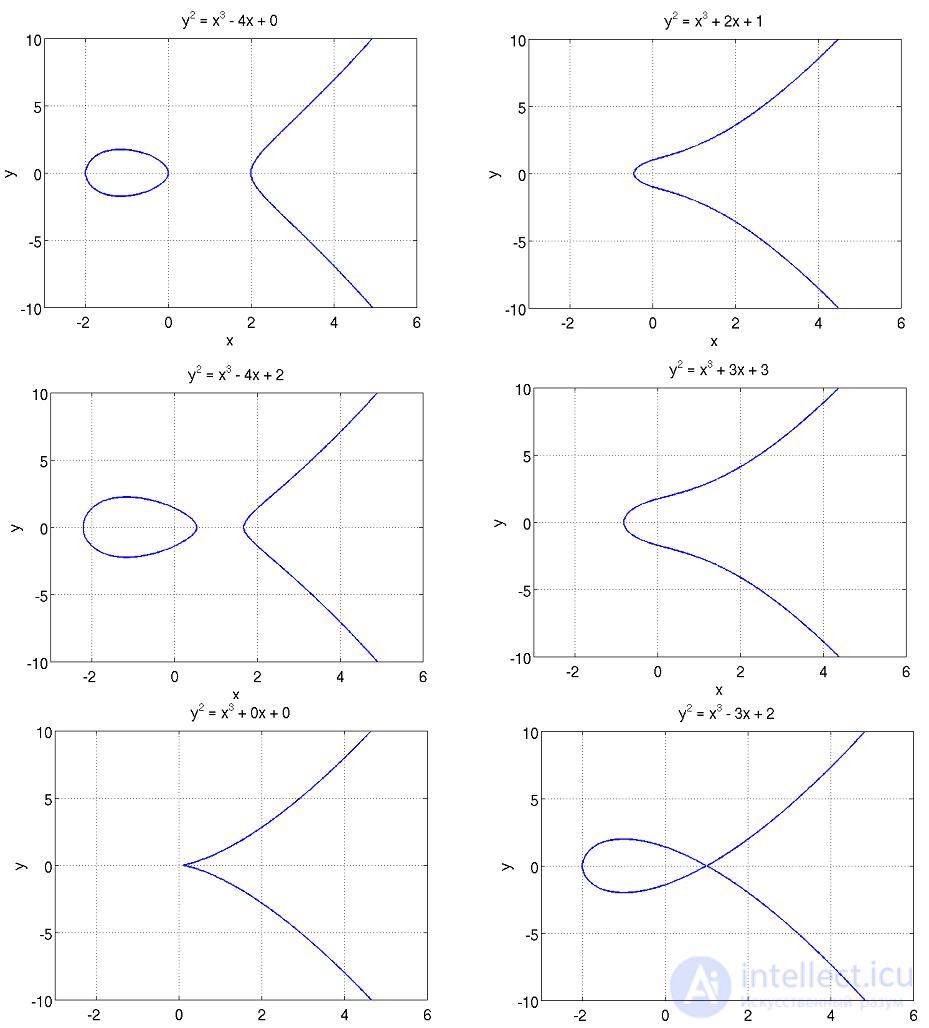
Эллиптические кривые представленые на первых 4-х рисунках называются гладкими. В то время как две нижние кривые относятся к т.н. сингулярным эллиптическим кривым.
Для гладких эллиптических кривых выполняется следующее неравенство:

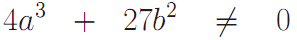
Тогда как для сингулярных кривых это условие, сюрприз, не выполняется.
Если вы собираетесь самостоятельно разрабатывать криптографических продукт, поддерживающий «эллиптику» очень важно запомнить следующий факт:
Нельзя использовать в схемах ЭЦП сингулярные кривые. Подробно мы еще затронем эту тему, сейчас же просто скажем, что используя сингулярные кривые вы рискуете значительно снизить стойкость схемы ЭЦП.
Арифметические операции в эллиптической криптографии производятся над точками кривой. Основной операцией является «сложение».
Сложение двух точек легко представить графически:

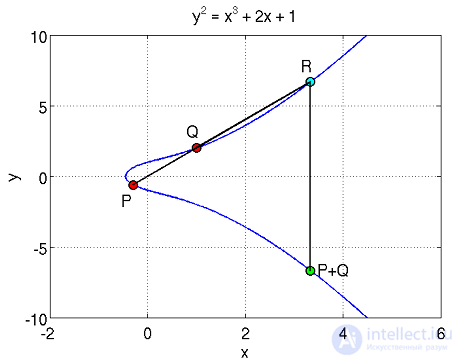
Как видно из рисунка, для сложения точек P и Q, необходимо провести между ними прямую линию, которая обязательно пересечет кривую в какой-либо третьей точке R. Отразим точку R относительно горизонтальной оси координат и получим искомую точку P+Q.

Алгебраическое представление «сложения»

Запишем сложение двух точек в виде формулы:

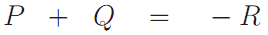
Пусть координатами точки P будут (xp, yp), а координатами точки Q соответственно (xq, yq). Вычислим

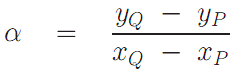
и тогда координаты точки P+Q будут равны:

Эллиптические кривые в криптографии

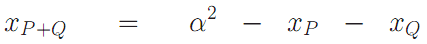
Осталось уточнить всего одну деталь. Все рассмотренные выше кривые относятся к эллиптическим кривым над вещественными числами. И это приводит нас к проблеме округления. Т.е., используя кривые над вещественными числами, мы не сможем получить биекцию между исходным текстом и зашифрованными данными. Чтобы не заморачиваться с округлением в криптографии используются только кривые над конечными полями. Это означает, что под эллиптической кривой понимается набор точек, чьи координаты принадлежат конечному полю.

В криптографии рассматривается два вида эллиптических кривых: над конечным полем 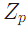— кольцо вычетов по модулю простого числа. Об этом говорит сайт https://intellect.icu . И над полем — бинарное конечное поле.
У эллиптических кривых над полем есть одно важное преимущество, элементы поля могут быть легко представленны в виде n-битных кодовых слов, это позволяет увеличить скорость аппаратной реализации эллиптических алгоритмов.

Все математические операции на эллиптических кривых над конечным полем производятся по законам конечного поля над которым построена эллиптическая кривая. Т.е. для вычисления, например, суммы двух точек кривой E над кольцом вычетов 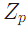все операции производятся по модулю числа p.

Однако здесь есть свои подводные камни. Если мы сложим два одинаковых элемента из бинарного конечного поля, то получим в результате 0, т.к. сложение происходит по модулю 2. Это означает что характеристика такого поля равна 2. Но эллиптическая кривая вида

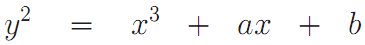
описанная над полем характеристики 2 или 3 становится сингулярной, а как уже замечалось выше это неудачная идея использовать сингулярные кривые в криптографии.

Поэтому над бинарным конечным полем используются кривые вида:


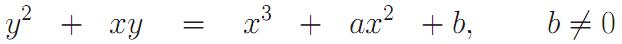
Еще одним важным понятие эллиптической криптографии является порядок эллиптической кривой, который показывает количество точек кривой над конечным полем.
Теорема Хассе утверждает, что если N — количество точек кривой, определенной над полем Zq с q элементами тогда справедливо равенство:


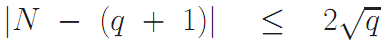
Т.к. бинарное конечное поле 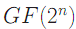состоит из 2n элементов мы можем сказать, что порядок кривой равен 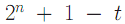, где .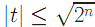

С числом t связано следующее определение:
эллиптическая кривая над бинарным конечным полем называется суперсингулярной, если t делится на характеристику поле(в случае бинарного поля характеристика равна 2) без остатка.
Разумеется все это я к тому, что нельзя использовать в схемах ЭЦП суперсингулярные кривые. Строгая рекомендация не использовать сингулярные и суперсингулярные кривые для цифровой подписи имеет одну очень вескую причину, но об этом позже.

Криптография на эллиптических кривых

Точки эллиптической кривой над конечным полем представляют собой группу. И как мы отмечали выше для этой группы определена операция сложения.
Соответственно мы можем представить умножение числа k на точку G как G+G+..+G с k слагаемыми.

Теперь представим, что у нас имеется сообщение M представленное в виде целого числа. Мы можем зашифровать его используя выражение
C=M*G.
Вопрос в том, насколько сложно восстановить M зная параметры кривой E(a,b), шифротекст С и точку G.
Данная задача называется дискретным логарифмом на эллиптической кривой и не имеет быстрого решения. Более того, считается, что задача дискретного логарифма на эллиптической кривой является более трудной для решения, чем задача дискретного логарифмирования в конечных полях.

Наиболее быстрые методы, разработанные для конечных полей оказываются бесполезны в случае эллиптических кривых.
Так для решения дискретного логарифма существуют достаточно быстрые алгоритмы имеющие сложность 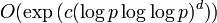, где c и d — некоторые константы, а p — размер поля. Такие алгоритмы называются субэкспоненциальными и позволяют сравнительно легко вскрывать дискретный логарифм в конечном поле, если размер поля не выбран очень большим, порядка 21024.
В тоже время наиболее быстрые методы решения дискретного логарифма на эллиптической кривой имеют сложность 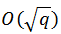, где q — количество точек эллиптической кривой.
Таким образом, для обеспечения уровня стойкости в 280 операций необходимо чтобы q=2160. Напомню, для того, чтобы получить аналогичный уровень сложности при вычислении дискретного логарифма в конечном поле необходимо поле порядка q=21024.

Следует, однако, заметить, что поскольку мощность вычислительной техники постоянно повышается, значение q будет постоянно увеличиваться. Но так как графики функци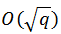й и 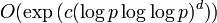резко отличаются друг от друга, в группе точек эллиптической кривой q будет расти намного медленнее, чем в произвольном конечном поле.

Варианты атак

1. Алгоритма Полига-Хеллмана. Алгоритм решения дискретного логарифма. Предположим, что n — количество точек эллиптической кривой. Пусть число n раскладывается на простые числа p1, p2,.., pn. Суть метода сводится к тому, чтобы найти дискретные логарифмы по модулю числе pi, а затем получить общее решение с помощью китайской теоремы об остатках. Атака позволяет свести проблему дискретного логарифма в большом поле n к той же задаче, но с гораздо меньшим полем p. Для того, чтобы противостоять атаке необходимо просто выбирать кривые, количество точек которых делится на очень большое простое число q≈n.
2. Алгоритм Шенкса, более известный как шаги младенца/шаги гиганта. Типичный пример time memory trade off. Для группы размером n вычисляется таблиц размером n1/2, затем по этой таблице происходит поиск нужного элемента. Сложность алгоритма .
3. Уязвимость сингулярных и суперсингулярных кривых. Я уже упоминал, что для решения задачи дискретного логарифма не существует субэкспоненциальных методов решения. На самом деле есть одна оговорка, такие методы есть, но только для определенного рода кривых: сингулярных и суперсингулярных. Особые свойства таких кривых позволяют свести задачу дискретного логарифма на эллиптической кривой, к задаче дискретного логарифма в конечном поле. Соответственно для такого класса кривых стандартные ключи размером в 160-320 бит, будут фатально уязвимы, что позволит злоумышленникам вскрыть секретный ключ, за относительно небольшое время.
4. Уязвимость аномальных кривых Напомню, что количество точек эллиптической кривой вычисляется по формуле
   n=q+1-t, где q — размер исходного поля. И что кривая называется суперсингулярной если t делится на 2.
   Поэтому, на первый взгляд может показаться хорошей идеей использовать кривые в которых количество точек равно q, т.е. t=1.
   Однако такие кривые называются аномальными и решение дискретного логарифма на аномальных эллиптических кривых является еще более простой задачей, чем для суперсингулярных и сингулярных кривых.

Подытожим

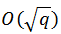На основании всего вышесказанного выпишем основные достоинства и недостатки эллиптической криптографии:
Итак, основные плюсы:

1. Гораздо меньшая длина ключа по сравнению к «классической» асимметричной криптографией.
2. Скорость работы эллиптических алгоритмов гораздо выше, чем у классических. Это объясняется как размерами поля, так и применением более близкой для компьютеров структуры бинарного конечного поля.
3. Из-за маленькой длины ключа и высокой скорости работы, алгоритмы асимметричной криптографии на эллиптических кривых могут использоваться в смарт-картах и других устройствах с ограниченными вычислительными ресурсами.

Основные минусы эллиптической криптографии:

1. Все плюсы эллиптической криптографии вытекают из одного конкретного факта:
   для задачи дискретного логарифмирования на эллиптических кривых не существует субэкспоненциальных алгоритмов решения. Это позволяет уменьшить длину ключа и увеличить производительность. Однако если такие алгоритмы появятся, то это будет означать крах эллиптической криптографии.
2. Эллиптическая криптография — это очень сложно. Не то чтобы я считал обычную асимметричную криптографию совсем уж простой штукой. Но «эллиптика» — это огромное количество тонкостей, которые необходимо учесть. Начиная с выбора эллиптической кривой и заканчивая генерацией ключей. При массовом переходе на эллиптику скорее всего обязательно будет большое количество ошибок и уязвимостей, которые уже отработаны для более привычных методов.

На основании всего вышесказанного, я сделал для себя вывод, что повсеместный переход на «эллиптику» не является необходимостью. В конце концов, пока мирно сосуществуют обычные RSA, DSA с одной стороны, и ГОСТ 34.10, ECDSA с другой, есть пусть и ложное, но успокаивающее чувство альтернативы, которого мы можем лишиться, погнавшись за самыми современными криптографическими методами.

Используемая литература

1. Don Johnson, Alfred Menezes, Scott Vanstone — The Elliptic Curve Digital Signature Algorithm.
2. А. Болотов, С. Гашков, А. Фролов, А. Часовских — Элементарное введение в эллиптическую криптографию.
3. Lawrence Washington — Elliptic curves, Number theory and Cryptography.

Исследование, описанное в статье про эллиптическая криптография, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое эллиптическая криптография, эллиптические кривые и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Шифры в криптографии