Лекция
Привет, Вы узнаете о том , что такое электрические фильтры, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электрические фильтры, , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники. Кликните на вариант (или варианты ответов), если он правильный - то будет подсвечен зеленым цветом и вам будет зачислено пару монеток, а если неверный - то красным и будет снята монетка. Удачи в прохождении онлайн теста!
Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.
Фильтр в электронике — устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных.
Электрический фильтр - это устройство или система, которая используется для фильтрации электрических сигналов или электромагнитных волн с целью извлечения нужной информации из шума, помех или других нежелательных сигналов.
В зависимости от типа фильтра, он может быть спроектирован для подавления или ослабления определенных частот сигнала или же для пропуска только частот, находящихся в определенном диапазоне. электрические фильтры широко используются в различных областях, включая радиоэлектронику, телекоммуникации, аудио- и видеотехнику, медицинскую технику, автомобильную промышленность и т.д.
Наиболее насправстронненный тип - Полосовой фильтр — фильтр, который пропускает составляющие, находящиеся в некоторой полосе частот.
Полосовой фильтр — линейная система и может быть представлен в виде последовательности, состоящей из фильтра верхних частот и фильтра нижних частот.
Идеальные полосовые фильтры характеризуются двумя характеристиками
В свою очередь, реализация полосового фильтра характеризуется шестью характеристиками
а также
Примером реализации такого фильтра может служить колебательный контур (цепь из последовательно соединенных резистора, конденсатора и индуктивности).
Существует несколько типов электрических фильтров, включая
Каждый тип фильтра имеет свои преимущества и недостатки, и выбор конкретного типа зависит от требований к конкретной системе или приложению.
Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим затуханием, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.
В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.
Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
 ), а емкостные проводимости конденсаторов много больше их активных проводимостей (
), а емкостные проводимости конденсаторов много больше их активных проводимостей (  ).
).Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т- или П-образной схеме, т.е. при 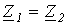 или
или 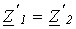 (см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.
(см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров
|
Название фильтра |
Диапазон пропускаемых частот |
|
Низкочастотный фильтр (фильтр нижних частот) |
|
|
Высокочастотный фильтр (фильтр верхних частот) |
|
|
Полосовой фильтр (полосно-пропускающий фильтр) |
|
|
Режекторный фильтр (полосно-задерживающий фильтр) |
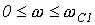 и и 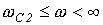 , где , где 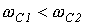 |
В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет нагрузку, сопротивление которой при всех частотах равно характеристическому, то напряжения и соответственно токи на его входе и выходе связаны соотношением
.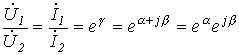 . . |
(1) |
В идеальном случае в полосе пропускания (прозрачности) 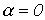 , т.е. в соответствии с (1)
, т.е. в соответствии с (1) 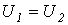 ,
, 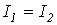 и
и 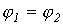 . Следовательно, справедливо и равенство
. Следовательно, справедливо и равенство  , которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае
, которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае 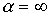 , т.е.
, т.е. 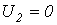 и
и 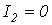 .
.
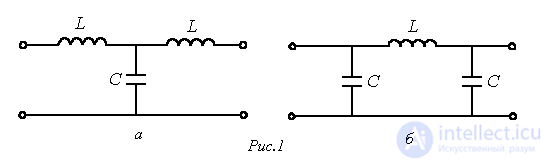
Рассмотрим схему простейшего низкочастотного фильтра, представленную на рис. 1,а.
Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)
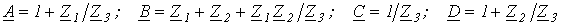
или конкретно для фильтра на рис. 1,а
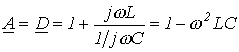 ; ; |
(2) |
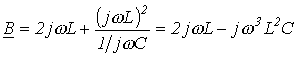 ; ; |
(3) |
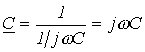 . . |
(4) |
Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что
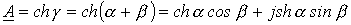 .
.
Однако в соответствии с (2) 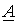 - вещественная переменная, а следовательно,
- вещественная переменная, а следовательно,
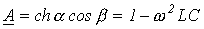 . . |
(5) |
Поскольку в полосе пропускания частот коэффициент затухания 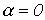 , то на основании (5)
, то на основании (5)
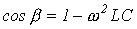 .
.
Так как пределы изменения 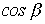 :
: 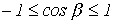 , - то границы полосы пропускания определяются неравенством
, - то границы полосы пропускания определяются неравенством
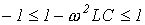 ,
,
которому удовлетворяют частоты, лежащие в диапазоне
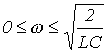 . . |
(6) |
Для характеристического сопротивления фильтра на основании (3) и (4) имеем
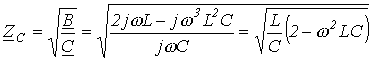 . . |
(7) |
Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно  , то, вследствие вещественности
, то, вследствие вещественности  , можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших
, можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших 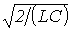 , как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.
, как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.
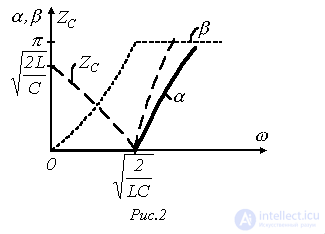
На рис. 2 приведены качественные зависимости 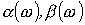 и
и 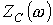 .
.
Следует отметить, что вне полосы пропускания 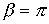 . Об этом говорит сайт https://intellect.icu . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство
. Об этом говорит сайт https://intellect.icu . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство
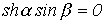 . . |
(8) |
Так как вне полосы прозрачности 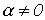 , то соотношение (8) может выполняться только при
, то соотношение (8) может выполняться только при 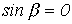 .
.
В полосе задерживания коэффициент затухания 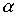 определяется из уравнения (5) при
определяется из уравнения (5) при 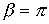 . Существенным при этом является факт постепенного нарастания
. Существенным при этом является факт постепенного нарастания 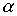 , т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания
, т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания 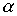 будет отличен от нуля.
будет отличен от нуля.
Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник по схеме на рис. 1,б.
Схема простейшего высокочастотного фильтра приведена на рис. 3,а.
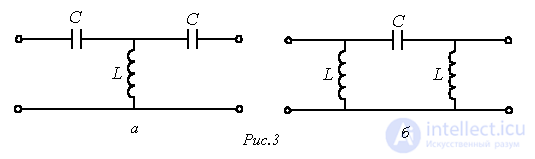
Для данного фильтра коэффициенты четырехполюсника определяются выражениями
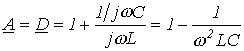 ; ; |
(9) |
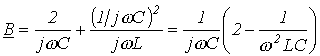 ; ; |
(10) |
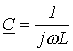 . . |
(11) |
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)
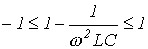 .
.
Данному неравенству удовлетворяет диапазон изменения частот
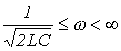 . . |
(12) |
Характеристическое сопротивление фильтра
 , , |
(13) |
изменяясь в пределах от нуля до 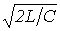 с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с
с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с  в ограниченном диапазоне частот.
в ограниченном диапазоне частот.
Вне области пропускания частот 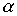 определяется из уравнения
определяется из уравнения
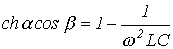 |
(14) |
при 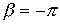 . Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.
. Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.
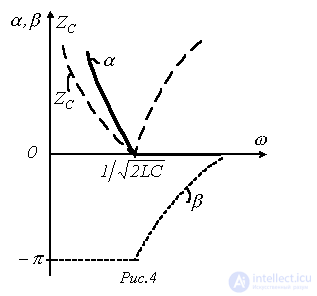
Качественный вид зависимостей 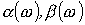 и
и 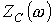 для низкочастотного фильтра представлен на рис. 4.
для низкочастотного фильтра представлен на рис. 4.
Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.
Полосовой фильтр формально получается путем последовательного соединения низкочастотного фильтра с полосой пропускания 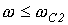 и высокочастотного с полосой пропускания
и высокочастотного с полосой пропускания 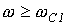 , причем
, причем 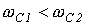 . Схема простейшего полосового фильтра
. Схема простейшего полосового фильтра
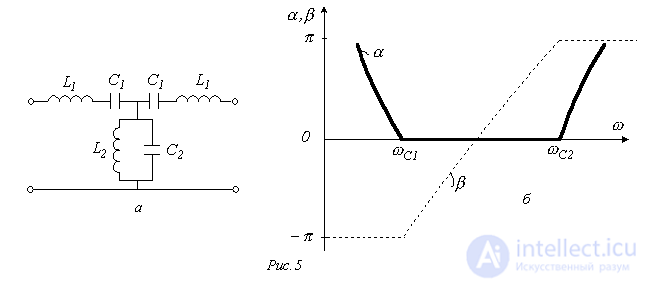
приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости 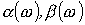 для него.
для него.
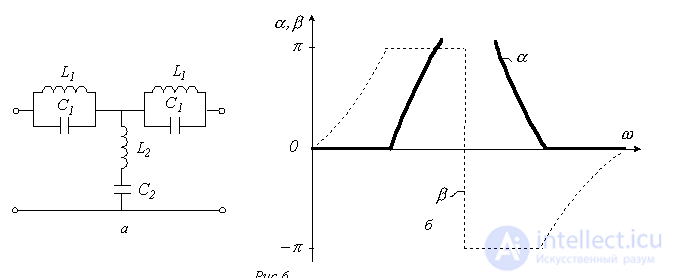
У режекторного фильтра полоса прозрачности разделена на две части полосой затухания. Схема простейшего режекторного фильтра и качественные зависимости 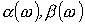 для него приведены на рис.6.
для него приведены на рис.6.
В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадно включенные четырехполюсники. При обеспечении согласованного режима работы всех n звеньев схемы коэффициент затухания 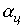 такого фильтра возрастает в соответствии с выражением
такого фильтра возрастает в соответствии с выражением 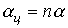 , что приближает фильтр к идеальному.
, что приближает фильтр к идеальному.
Фильтры, находящие применение в обработке сигналов, бывают
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры (по виду передаточной функции):
По порядку (степени уравнения) передаточной функции (см. также ЛАФЧХ ) различают фильтры первого, второго и более высоких порядков . Крутизна ЛАЧХ фильтра 1-го порядка в полосе подавления равна 20 дБ на декаду, фильтра 2-го порядка — 40 дБ на декаду, и т. д.
По тому, какие частоты фильтром пропускаются (задерживаются), фильтры подразделяются на
В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределенные реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник составляющих спектра (они могут не являться гармониками) с нужными частотами. Другой принцип построения пассивных аналоговых фильтров — это использование механических (акустических) колебаний в механическом резонаторе той или иной конструкции.
В качестве простейших фильтров низких и высоких частот могут использоваться RC-цепь или LR-цепь . Однако они имеют невысокую крутизну АЧХ в полосе подавления, недостаточную во многих случаях: всего 6 дБ на октаву (или 20 дБ на декаду) — для RC-фильтра, являющегося фильтром 1-го порядка и 40 дБ/декада для LC-фильтра, являющегося фильтром 2-го порядка. В пассивных фильтрах добавление в схему фильтра любого реактивного компонента увеличивает порядок фильтра на 1.
Простейший фильтр нижних частот 1-го порядка изображен на рисунке и состоит из последовательно соединенных резистора и конденсатора
, образующего делитель напряжения входного сигнала. Комплексный коэффициент передачи
такого делителя:
где — постоянная времени RС-цепи.
Модуль коэффициента передачи этой цепи:
где
При входной частоте модуль коэффициента передачи близок к 1, при
модуль коэффициента передачи близок к 0, на частоте
модуль коэффициента передачи равен
— уменьшение относительно единичного коэффициента передачи приблизительно на 3,01 дБ, эта частота называется частотой среза фильтра. В полосе подавления при частоте много выше частоты среза модуль коэффициента передачи уменьшается на 20 дБ на декаду изменения частоты.
На рисунке показан пример простейшего LC-фильтра нижних частот 2-го порядка: при подаче гармонического сигнала определенной частоты на вход фильтра (на рисунке справа) напряжение на выходе фильтра (справа) в установившемся режиме определяется отношением реактивных сопротивлений катушки индуктивности ( ) и конденсатора (
).
Коэффициент передачи ФНЧ можно вычислить, рассматривая этот фильтр как делитель напряжения, образованный реактивными сопротивлениями.
Комплексное (с учетом сдвига фаз между напряжением и током) сопротивление катушки индуктивности есть и комплексное сопротивление конденсатора
, где
— мнимая единица ,
— угловая частота входного гармонического сигнала, поэтому для ненагруженного LC-фильтра коэффициент передачи � будет выражаться формулой для делителя напряжения:
.
Подставляя в формулу выражения для комплексных сопротивлений, получим для частотно-зависимого коэффициента передачи:
.
Как видно, коэффициент передачи ненагруженного идеального ФНЧ источником сигнала для которого является идеальный генератор напряжения с нулевым внутренним сопротивлением неограниченно растет с приближением к резонансной частоте , так как знаменатель выражения стремится к нулю. При повышении частоты выше резонансной — убывает. На очень низких частотах коэффициент передачи ФНЧ близок к единице, на очень высоких — к нулю.
Принято называть зависимость модуля комплексного коэффициента передачи фильтра от частоты амлитудно-частотной характеристикой (АЧХ), а зависимость фазы от частоты — фазо-частотной характеристикой (ФЧХ).
В реальных схемах к выходу фильтра подключается активная нагрузка , которая понижает добротность фильтра и устраняет острый всплеск коэффициента передачи вблизи частоты резонанса .
Величину называют характеристическим сопротивлением фильтра или волновым сопротивлением фильтра. Если ФНЧ нагрузить на активное сопротивление, равное характеристическому, то передаточная функция станет нерезонансной, коэффициент передачи будет примерно постоянный для частот
, и убывающий как
на частотах выше
. На частоте
коэффициент передачи такого ФНЧ уменьшается на 3 дБ относительно значения коэффициента передачи на низкой частоте, эту частоту называют частотой среза фильтра. На частотах много выше частоты среза коэффициент передачи уменьшается на 40 дБ на декаду изменения частоты.
Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор . Для ненагруженного ФВЧ получается выражение для коэффициента передачи:
.
На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице.
На сверхвысоких частотах сосредоточенные элементы ( конденсаторы и катушки индуктивности) практически не используются, так как с ростом частоты их типичные для этого диапазона номиналы, а следовательно и габариты, уменьшаются настолько, что изготовление их становится невозможным. Поэтому применяются так называемые линии с распределенными параметрами, в которых индуктивность , емкость и активная нагрузка равномерно или неравномерно распределены по всей линии. Так, элементарный ФНЧ, рассматриваемый в предыдущем разделе, состоит из двух сосредоточенных элементов, представляющих собой резонатор; в случае же распределенных параметров фильтр будет состоять из одного элемента-резонатора (например отрезка микрополосковой линии или металлического стержня).
Конструкции СВЧ фильтров весьма разнообразны, и выбор конкретной реализации зависит от предъявляемых к устройству требований (значение рабочих частот, добротность, максимальное затухание в полосе задержания, расположение паразитных полос пропускания).
Проектирование фильтров на распределенных параметрах является достаточно сложным процессом, состоящим из двух этапов: получение электрических параметров, исходя из требований к устройству; получение габаритных параметров из полученных электрических. В основе современных методов проектирования микроволновых фильтров лежит теория связанных резонаторов.
Электромеханический фильтр (ЭМФ) содержит механическую резонансную систему (резонатор) той или иной конструкции. На входе и на выходе фильтра стоят электромеханические преобразователи, которые преобразуют электрические колебания сигнала в механические колебания рабочего тела фильтра и обратно.
ЭМФ получили распространение в трактах промежуточной частоты высококачественных радиосистем (в том числе военных, морских, радиолюбительских и других). Их преимуществом является значительно бо́льшая, чем у эквивалентных LC-фильтров, добротность, позволяющая достичь высокой избирательности, необходимой для разделения близких по частоте радиосигналов в приемниках.
Активные аналоговые фильтры строятся на основе усилителей, охваченных петлей обратной связи (положительной или отрицательной). В активных фильтрах возможно избежать применения катушек индуктивности, что позволяет уменьшить физические размеры устройств, упростить и удешевить их изготовление.
LC-фильтры используются в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя. В каскадах радиоэлектронной аппаратуры часто применяются перестраиваемые LC-фильтры, например, простейший LC-контур, включенный на входе средневолнового радиоприемника обеспечивает настройку на определенную радиостанцию.
Фильтры используются в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ , для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах, в схемах частотной коррекции магнитофонов и др.
 ,
,  .
.
1. Что такое электрический фильтр?
2. Какой тип фильтра используется для подавления определенных частот сигнала?
3. Какой тип фильтра используется для пропуска только частот, находящихся в определенном диапазоне?
4. Какой параметр характеризует способность фильтра подавлять сигналы вне заданного диапазона?
5. Какой тип фильтра имеет наименьшую добротность?
6. Какой тип фильтра используется для усиления определенных частот сигнала?
. Активный и цифровой фильтры не предназначены для усиления определенных частот сигнала, а скорее для фильтрации или обработки сигнала. Фильтр усиления не является стандартным типом фильтра.
7. Какой параметр характеризует ширину полосы пропускания фильтра?
8. Какой тип фильтра используется для снижения уровня шума в электрическом сигнале?
9.Какой параметр характеризует отношение максимального сигнала к уровню шума на выходе фильтра?
10. Какой тип фильтра обладает наибольшей добротностью?
Исследование, описанное в статье про электрические фильтры, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электрические фильтры, и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники