Лекция
Привет, Вы узнаете о том , что такое способы составления характеристического уравнения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое способы составления характеристического уравнения , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 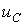 на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.
на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.

Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
jw заменяется на оператор р;
полученное выражение 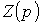 приравнивается к нулю.
приравнивается к нулю.
Уравнение
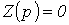
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника
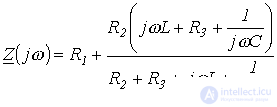 .
.
Заменив jw на р и приравняв полученное выражение к нулю, запишем
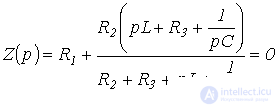
или
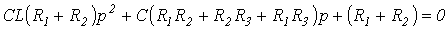 . . |
(1) |
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
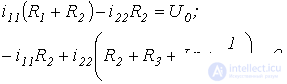
Отсюда выражение для главного определителя этой системы
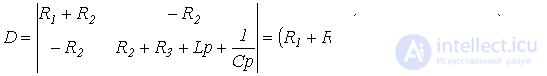 .
.
Приравняв D к нулю, получим результат, аналогичный (1).
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
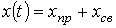 . . |
(2) |
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Рассмотрим два случая:
а) 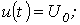
б)  .
.
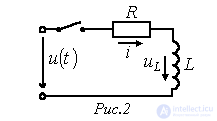
Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
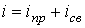 . . |
(3) |
Тогда для первого случая принужденная составляющая тока
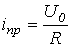 . . |
(4) |
Характеристическое уравнение
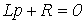 ,
,
откуда 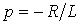 и постоянная времени
и постоянная времени 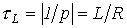 .
.
Таким образом,
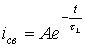 . . |
(5) |
Подставляя (4) и (5) в соотношение (3), запишем
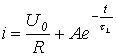 .
.
В соответствии с первым законом коммутации 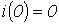 . Об этом говорит сайт https://intellect.icu . Тогда
. Об этом говорит сайт https://intellect.icu . Тогда
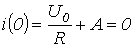 ,
,
откуда 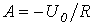 .
.
Таким образом, ток в цепи в переходном процессе описывается уравнением
 ,
,
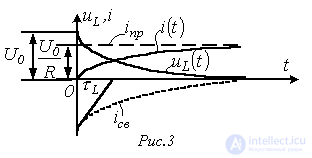
а напряжение на катушке индуктивности – выражением
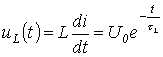 .
.
Качественный вид кривых 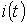 и
и 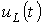 , соответствующих полученным решениям, представлен на рис. 3.
, соответствующих полученным решениям, представлен на рис. 3.
При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:
 ,
,
где 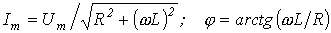 .
.
Отсюда
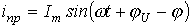 .
.
Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,
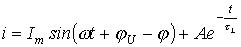 .
.
Поскольку 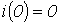 , то
, то
 .
.
Таким образом, окончательно получаем
 . . |
(6) |
Анализ полученного выражения (6) показывает:
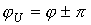 постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.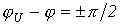 свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.Если 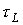 значительна по величине, то за полпериода свободная составляющая существенно не уменьшается. В этом случае максимальная величина тока переходного процесса
значительна по величине, то за полпериода свободная составляющая существенно не уменьшается. В этом случае максимальная величина тока переходного процесса 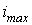 может существенно превышать амплитуду тока установившегося режима. Как видно из рис. 4, где
может существенно превышать амплитуду тока установившегося режима. Как видно из рис. 4, где
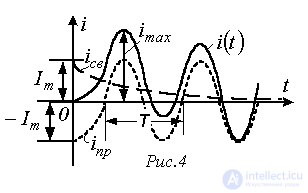
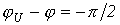 , максимум тока имеет место примерно через
, максимум тока имеет место примерно через 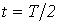 . В пределе при
. В пределе при 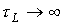
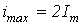 .
.
Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: 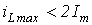 .
.
Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени 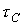 цепи достаточно велика, то примерно через половину периода напряжение на конденсаторе достигает своего максимального значения
цепи достаточно велика, то примерно через половину периода напряжение на конденсаторе достигает своего максимального значения 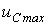 , которое не может превышать удвоенной амплитуды принужденного напряжения:
, которое не может превышать удвоенной амплитуды принужденного напряжения: 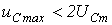 .
.
2. Переходные процессы при отключении катушки индуктивности от источника питания
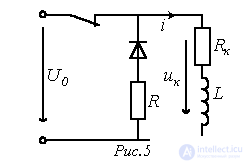
При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности 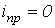 .
.
Характеристическое уравнение
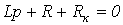 ,
,
откуда  и
и 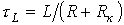 .
.
В соответствии с первым законом коммутации
 .
.
Таким образом, выражение для тока в переходном режиме
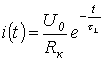
и напряжение на катушке индуктивности
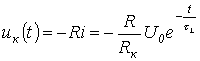 . . |
(7) |
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при  модуль напряжения на катушке индуктивности в момент коммутации будет во много раз превышать напряжение источника:
модуль напряжения на катушке индуктивности в момент коммутации будет во много раз превышать напряжение источника: 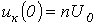 . При отсутствии гасящего резистора R указанное напряжение прикладывается к размыкающимся контактам ключа, в результате чего между ними возникает дуга.
. При отсутствии гасящего резистора R указанное напряжение прикладывается к размыкающимся контактам ключа, в результате чего между ними возникает дуга.
3. Заряд и разряд конденсатора

При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:
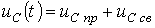 .
.
Принужденная составляющая напряжения на конденсаторе 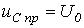 .
.
Из характеристического уравнения
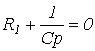
определяется корень 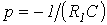 . Отсюда постоянная времени
. Отсюда постоянная времени 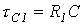 .
.
Таким образом,
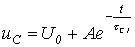 .
.
При t=0 напряжение на конденсаторе равно 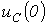 (в общем случае к моменту коммутации конденсатор может быть заряженным, т.е.
(в общем случае к моменту коммутации конденсатор может быть заряженным, т.е. 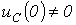 ). Тогда
). Тогда 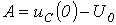 и
и
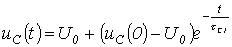 .
.
Соответственно для зарядного тока можно записать
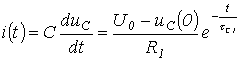 .
.
В зависимости от величины 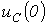 : 1 -
: 1 - 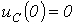 ; 2 -
; 2 - 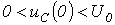 ; 3 -
; 3 - 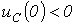 ; 4 -
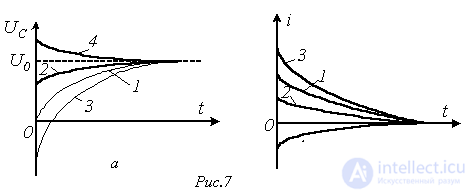
; 4 -  - возможны четыре вида кривых переходного процесса, которые иллюстрирует рис. 7.
- возможны четыре вида кривых переходного процесса, которые иллюстрирует рис. 7.
При разряде конденсатора на резистор 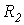 (ключ на рис.6 переводится в положение 2)
(ключ на рис.6 переводится в положение 2) 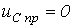 . Постоянная времени
. Постоянная времени 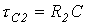 .
.
Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения 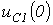 (в частном случае
(в частном случае 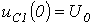 ), для напряжения на нем в переходном режиме можно записать
), для напряжения на нем в переходном режиме можно записать
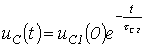 .
.
Соответственно разрядный ток
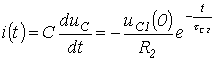 . . |
(8) |
Как видно из (8), во избежание значительных бросков разрядного тока величина 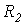 должна быть достаточно большой.
должна быть достаточно большой.
В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.
Литература
Контрольные вопросы
Ответ: 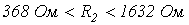 .
.
Ответ: 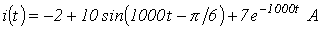 .
.
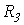 .
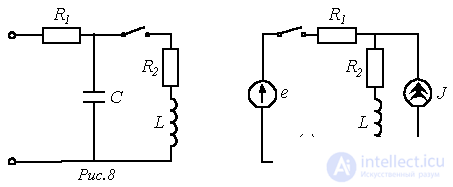
.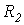 переходный процесс в ней будет носить апериодический характер, если
переходный процесс в ней будет носить апериодический характер, если 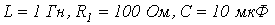 .
.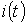 в цепи на рис. 9, если
в цепи на рис. 9, если 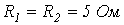 ,
, 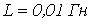 ,
, 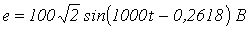 ,
, 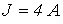 .
.Исследование, описанное в статье про способы составления характеристического уравнения, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое способы составления характеристического уравнения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники