Лекция
Привет, Вы узнаете о том , что такое операторный метод расчета переходных процессов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое операторный метод расчета переходных процессов , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
Сущность операторного метода заключается в том, что функции  вещественной переменной t, которую называют оригиналом, ставится в соответствие функция
вещественной переменной t, которую называют оригиналом, ставится в соответствие функция 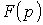 комплексной переменной
комплексной переменной  , которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
В общем случае порядок расчета переходных процессов операторным методом следующий:
1) Составляется операторная схема замещения цепи, сложившейся после коммутации по правилу, приведенному в таблице 1. Выбираются положительные направления токов в ветвях.
2) Определяется докоммутационное состояние цепи (определяются токи в индуктивностях и напряжения на емкостях до коммутации).
3) Любым способом расчета (с помощью уравнений Кирхгофа, методом контурных токов, методом узловых потенциалов, и т.д.) определяется операторное изображение искомой величины.
4) На основе полученного изображения находится оригинал искомой функции.
операторный метод расчета переходных процессов основывается на использовании линейного интегрального преобразования Лапласа, которое позволяет любые интегральные и дифференциальные временные соотношения свести к алгебраическим выражениям, получив систему алгебраических уравнений, зависимых от комплексной переменной р

f(t) – оригинал, F(p) – изображение, ≓ - символ соответствия между оригиналом и изображением по Лапласу. Каждой функции времени f(t) соответствует единственная функция переменной p: ( ) ≓ ( ), и наоборот, каждой функции переменной p соответствует только одна функция времени: ( ) ≓ ( ). Изображения наиболее часто используемых функций приведены в таблице 1.
Изображение  заданной функции
заданной функции 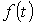 определяется в соответствии с прямым преобразованием Лапласа:
определяется в соответствии с прямым преобразованием Лапласа:
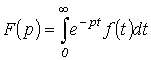 . . |
(1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
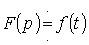 или
или 
Следует отметить, что если оригинал  увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля
увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля 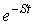 . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.
. Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Операторные типовых функций

Оригинал  |
Изображение  |
| A | 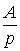 |
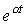 |
 |
 |
 |
 |
 |
 |
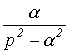 |
 |
 |
Некоторые свойства изображений
 .
.
 .
.
С использованием этих свойств и данных табл. 1, можно показать, например, что
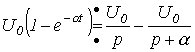 .
.
Изображения производной и интеграла
В курсе математики доказывается, что если  , то
, то 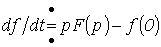 , где
, где  - начальное значение функции
- начальное значение функции  .
.
Таким образом, для напряжения на индуктивном элементе можно записать

или при нулевых начальных условиях
 .
.
Отсюда операторное сопротивление катушки индуктивности
 .
.
Аналогично для интеграла: если  , то
, то  .
.
С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:
 .
.
Тогда
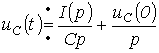
или при нулевых начальных условиях
 ,
,
откуда операторное сопротивление конденсатора
 .
.

Пусть имеем некоторую ветвь  (см. рис. 1), выделенную из некоторой
(см. рис. 1), выделенную из некоторой

сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:
 .
.
Тогда на основании приведенных выше соотношений получим:
 .
.
Отсюда
 , , |
(2) |
где  - операторное сопротивление рассматриваемого участка цепи.
- операторное сопротивление рассматриваемого участка цепи.
Следует обратить внимание, что операторное сопротивление 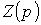 соответствует комплексному сопротивлению
соответствует комплексному сопротивлению  ветви в цепи синусоидального тока при замене оператора р на
ветви в цепи синусоидального тока при замене оператора р на 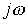 .
.
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.

Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю
 .
.
Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
 .
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде
 .
.

В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 -  ; 2 -
; 2 -  .
.
В первом случае в соответствии с законом Ома 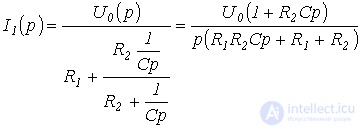 .
.
Тогда

и

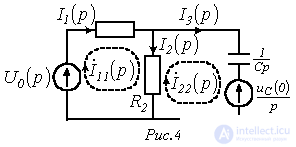
Во втором случае, т.е. при  , для цепи на рис. 3 следует составить операторную схему замещения, которая приведена на рис. 4. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:
, для цепи на рис. 3 следует составить операторную схему замещения, которая приведена на рис. 4. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:

откуда  ;
;  и
и  .
.
Существует три способа перехода от изображения к оригиналу. Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа Переход от изображения к оригиналу выполняется с помощью так называемого интеграла Римана - Мелина, являющегося формулой обратного преобразования Лапласа:
, 
которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:
 .
.
На практике этот способ применяется редко.
При этом ольшое значение имеют теоремы, позволяющие представить изображение в виде суммы более простых слагаемых и тем самым упростить переход от изображения к оригиналу.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала. Существуют справочники, содержащие несколько сотен изображений и соответствующих им оригиналов. Следует только изображение привести к табличному виду. При использовании готовых таблиц следует выяснить, с помощью какого преобразования они составлены - Лапласа или Карсона. Если изображение дается по Карсону, то его следует поделить на р для получения изображения по Лапласу.

Например, для изображения тока в цепи на рис. 5 можно записать
 .
.
Тогда в соответствии с данными табл. 1
 ,
,
что соответствует известному результату.
3. С использованием формулы разложения
Теорема разложения используется, когда изображение найдено в виде рациональной дроби:

Где F1(p) и F2(p) – полиномы относительно p
Пусть изображение  искомой переменной определяется отношением двух полиномов
искомой переменной определяется отношением двух полиномов
 ,
,
где  .
.
Это выражение может быть представлено в виде суммы простых дробей
 , , |
(3) |
где 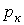 - к-й корень уравнения
- к-й корень уравнения  .
.
Для определения коэффициентов  умножим левую и правую части соотношения (3) на (
умножим левую и правую части соотношения (3) на (  ):
):
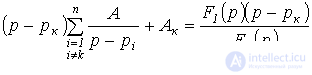 .
.
При 
 .
.
Рассматривая полученную неопределенность типа  по правилу Лопиталя, запишем
по правилу Лопиталя, запишем
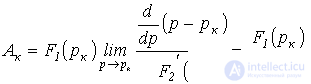 .
.
Таким образом,
 .
.
Поскольку отношение  есть постоянный коэффициент, то учитывая, что
есть постоянный коэффициент, то учитывая, что 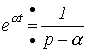 , окончательно получаем
, окончательно получаем
 . . |
(4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения  равен нулю, т.е.
равен нулю, т.е.  , то уравнение (4) сводится к виду
, то уравнение (4) сводится к виду
 .
.
В заключение раздела отметим, что для нахождения начального  и конечного
и конечного 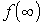 значений оригинала можно использовать предельные соотношения
значений оригинала можно использовать предельные соотношения

которые также могут служить для оценки правильности полученного изображения.
При работе с изображениями можно использовать свойства преобразования Лапласа, которые позволяют упростить операторное изображение искомой
функции. Очевидно, что соответствие между оригиналом и изображением взаимно однозначны, т. е. каждой функции f(t) соответствует одна вполне
определенная функция F(p) и наоборот. Приведены наиболее часто используемые свойства.
Свойство линейности. При умножении оригинала на постоянную величину на ту же постоянную величину умножается и изображение:
af(t) ≓ aF(p).
Если оригинал представлен суммой функций, то изображение этой суммы равно сумме изображений этих функций (изображение линейной комбинации
функций есть линейная комбинация изображений):

Теорема дифференцирования. Допустим, что некоторая функция f(t) имеет изображение F(p) , тогда изображение производной этой функции

Вычисление производной при нулевых начальных условиях (f(0) = 0) соответствует умножению изображения функции на множитель p:
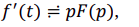
многократное дифференцирование при нулевых условиях:

Теорема интегрирования. Известно изображение некоторой функции f(t). Изображение функции, являющейся интегралом функции f(t) определяется

Многократному (n раз) интегрированию соответствует общее выражение:
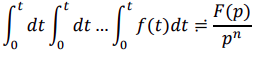
Теорема запаздывания. Теорема позволяет определить изображение функции f(t - t1) , отличающейся от функции f(t) тем, что она сдвинута
вправо вдоль оси времени на t1 (рис.1) :

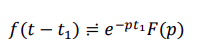

Таким образом, запаздывание функции на время t1 соответствует умножению ее изображения на 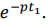 .
.
Теорема смещения. Теорема смещения позволяет определить, как изменяется изображение при умножении оригинала на показательную
функцию e ±at, где a - постоянное число.
Пусть новая функция имеет вид

Ее изображение

Таким образом, умножение временной функции на экспоненциальный множитель приводит к «смещению» в области изображений независимой
переменной p на p±a
Теорема умножения изображений (теорема свертки - интеграл Бореля).
Теорема заключается в следующем: если
 , то
, то

Таким образом, произведению изображений двух функций соответствует свертка их оригиналов. Теорема свертки широко используется при
составлении таблиц операторных соотношений. Если изображение искомой функции может быть представлено в виде произведения двух (или более)
сомножителей, то по оригиналам каждого из сомножителей можно вычислить оригинал исходной функции.
Теорема подобия. Теорема позволяет определить изображение функции времени при изменении масштаба ее аргумента. Пусть известно изображение
функции f( t) ≓ F(p ). Изображение функции j(t) = f (at) , где а - некоторая положительная постоянная, будет

Умножение аргумента оригинала на положительное постоянное число а приводит к делению аргумента изображения и самого изображения на то же
число а.
Решить задачу операторным методом. Схема цепи, параметры элементов и ЭДС следующие: Е=100 В, r=10 Ом, R1=40 Ом, R2=50 Ом, С=1000 мкФ. Найти токи в ветвях и напряжения на всех элементах цепи при замыкании ключа: i1(t), i2(t), i3(t), UR1(t), UR2(t), UС(t), Ur(t).

Решение.
1. Составляем операторную схему замещения для цепи после коммутации, пользуясь таблицей 1 (рис.3):

2. Определяем докоммутационное состояние цепи.
Здесь необходимо определить напряжение на емкости UC(0), зная, что по закону коммутации UC(0)=UC(0-). Для этого возвращаемся к рис.2. До
коммутации в цепи существует постоянный ток, который не протекает через емкость, поэтому мы заменяем ее на разрыв цепи. Значит, ток
замыкается в первом контуре. Схема приобретает вид (рис.4). Численное значение тока можно определить, составив для этого контура уравнение
по 2-му закону Кирхгофа: 

зажимам, что и R1 и R2 , то есть параллельно с этими резисторами, равно:

3. Определим операторные изображения искомых величин. Решать задачу можно любым известным способом (воспользоваться уравнениями
Кирхгофа, методом контурных токов, узловых потенциалов и пр.). Воспользуемся уравнениями Кирхгофа. В этой схеме три ветви и два
узла, поэтому необходимо составить одно узловое и два контурных уравнения:
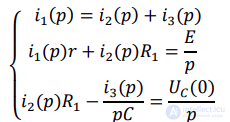
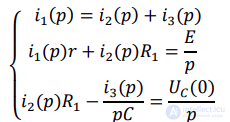 (5)
(5)
Теперь выразим ток i2(p) из второго уравнения системы через ток i1(p) :
 (6)
(6)
А затем, подставив

в третье уравнение системы (5), выразим ток i3(p) через ток i1(p):
 (7)
(7)
После этого можно подставить выражения (6) и (7) в первое уравнение, получив таким образом уравнение относительно i1(p)

Подставляя известные нам значения ЭДС Е, найденное в п.2 UC(0), значения сопротивлений и упрощая выражение, получим операторное изображение
тока i1:
 (8)
(8)
Теперь по формулам (6) и (7) можем определить операторные изображения токов i2(p) и i3(p):
 (9)
(9)

 (10)
(10)
4. Перейдем к оригиналам полученных величин, пользуясь разными способами.
- Сначала получим оригинал тока i1(t). Поскольку числитель и знаменатель полученного выражения (8) представляют собой полиномы от p, и дробь
является рациональной (порядок числителя меньше порядка знаменателя), то перейдем от изображения к оригиналу по теореме разложения.
-Запишем числитель:
 . , знаменатель
. , знаменатель 
 найдем производную знаменателя:
найдем производную знаменателя:


Приравняв знаменатель к нулю, определим его корни:
p1=0; p2= -125
Подставляя корни, найдем значения числителя и производной знаменателя:


Теперь можно получить оригинал тока i1(t) по формуле:

Интересно также получить оригинал тока i1(t) по теореме о вычетах, при этом также необходимо приравнять знаменатель к нулю и определить его корни. Количество определяемых вычетов (слагаемых) будет равно количеству корней:

- Перейдем к отысканию оригинала тока i2(t).
- Здесь необходимо обратить внимание на то, что выражение состоит из двух слагаемых и вспомнить свойство линейности: изображение
линейной комбинации функций есть линейная комбинация изображений. То есть будем искать оригинал первого слагаемого, а затем оригинал второго. Нетрудно увидеть, что оригинал первого представляет собой константу – 2.5. Оригинал второго слагаемого отыщем по теореме разложения.
Изображение тока i2:

Второе cлагаемое:

Корни знаменателя те же, поскольку переходный процесс един во всей цепи:  ,
,
1 . Запишем числитель: 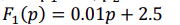
, знаменатель 
, найдем производную знаменателя: 
Подставляя корни, найдем значения числителя и производной знаменателя:


Теперь можно получить оригинал функции ψ(t)
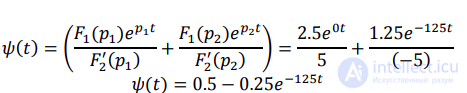
а затем и оригинал тока i2(t) по формуле:

- Получим оригинал тока i2(t) по теореме о вычетах:

Приведем оба слагаемых к общему знаменателю и упростим:

Найдем ток i2(t):

- Ток i3(t) можно искать разными способами: воспользовавшись первым уравнением из системы уравнений Кирхгофа, найти разность токов i1 и i2,
оперируя изображениями, а затем перейти к оригиналу; воспользоваться выражением (7), определить изображение этого тока и затем перейти к
оригиналу удобным способом; найти непосредственно разность оригиналов токов i1 и i2. Наиболее простыми представляются два последних:
-Изображение тока i3 из выражения (7):

В упрощенном виде:

Здесь при переходе к оригиналу также необходимо вспомнить свойство линейности: при умножении оригинала на постоянную величину на ту же
величину умножается и изображение, и наоборот.
По теореме разложения: 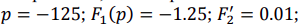

По теореме о вычетах:

- Вычитая непосредственно оригиналы:

Осталось определить напряжения на всех элементах этой схемы: UC, UR1, UR2,
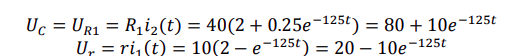
Напряжение на резисторе R2 изменилось до 0 в момент коммутации, и мы принимаем это изменение за мгновенное, как и сам процесс коммутации.
Напряжение на резисторе R1 до коммутации равно 40 В (UR1= IR1), а после нее равно напряжению на емкости.
С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.

Ответ:  .
.
8. С использованием предельных соотношений и решения предыдущей задачи найти начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ:  .
.
Исследование, описанное в статье про операторный метод расчета переходных процессов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое операторный метод расчета переходных процессов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники