24. Переходные процессы в линейных электрических цепях с сосредоточенными параметрами

Привет, Вы узнаете о том , что такое переходные процессы в линейных электрических цепях с сосредоточенными параметрами, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое переходные процессы в линейных электрических цепях с сосредоточенными параметрами , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.

При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.

Основные методы анализа переходных процессов в линейных цепях:

1. Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
2. Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
3. Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
4. Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
5. Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).

Классический метод расчета

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.

Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи

Резистор (идеальное активное сопротивление)

Катушка индуктивности (идеальная индуктивность)

; при наличии магнитной связи с катушкой, обтекаемой током ,

Конденсатор (идеальная емкость)

;

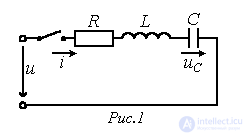
Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать

.

(1)

Подставив в (1) значение тока через конденсатор

,

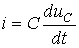получим линейное дифференциальное уравнение второго порядка относительно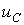

.

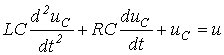В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:

,

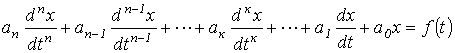(2)

где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); 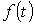- известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); 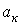- к-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.

В общем случае порядок дифференциального уравнения определяется соотношением

,

(3)

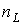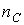где и - соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; 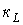- число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); 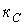- число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Об этом говорит сайт https://intellect.icu . Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение , соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).

Частное решение 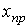уравнения (2) определяется видом функции 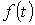, стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.

Вторая составляющая 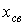общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная - свободной составляющей.

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид

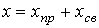(4)

Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.

Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.

Начальные условия. Законы коммутации

В соответствии с определением свободной составляющей 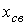в ее выражении имеют место постоянные интегрирования 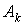, число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени 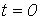(момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).

Таблица 2. Законы коммутации

Название закона	Формулировка закона
Первый закон коммутации (закон сохранения потокосцепления)	Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .
Второй закон коммутации (закон сохранения заряда)	Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения 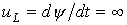и 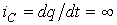, что приводит к нарушению законов Кирхгофа.

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:

первый закон коммутации – в ветви с катушкой индуктивности ток в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .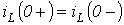

второй закон коммутации – напряжение на конденсаторе в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .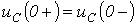

Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).

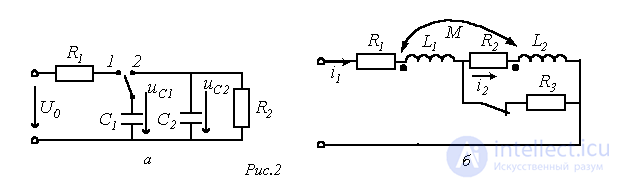
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа 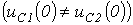. Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

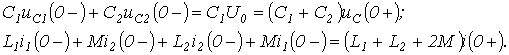
Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для 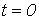. Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при .

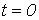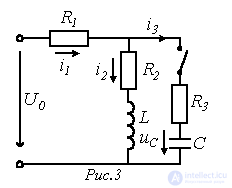
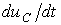Пример. Определить токи и производные и в момент коммутации в схеме на рис. 3, если до коммутации конденсатор был не заряжен.

В соответствии с законами коммутации

и .

На основании второго закона Кирхгофа для момента коммутации имеет место

,

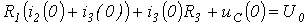откуда

и .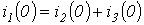

Для известных значени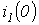й и 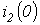из уравнения

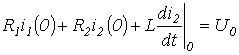
определяется .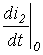

Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

.

Корни характеристического уравнения. Постоянная времени

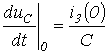Выражение свободной составляющей 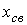общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).

Таблица 3. Выражения свободных составляющих общего решения

Вид корней характеристического уравнения	Выражение свободной составляющей
Корни вещественные и различные
Корни вещественные и
Пары комплексно-сопряженных корней

Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях 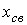монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

,

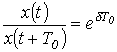которое называется декрементом колебания, или натуральным логарифмом этого отношения

,

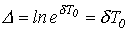называемым логарифмическим декрементом колебания, где .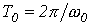

Важной характеристикой при исследовании переходных процессов является постоянная времени t, определяемая для цепей первого порядка, как:

,

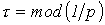где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при

Контрольные вопросы

1. Чем обусловлены переходные процессы?
2. Как определяется порядок дифференциального уравнения, описывающего переходный процесс?
3. Для каких цепей применим классический метод расчета переходных процессов?
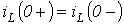4. Доказать законы коммутации: и 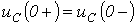- с энергетических позиций.
5. В каких цепях и почему возможен колебательный процесс?
6. Определить величину токов и напряжений на конденсаторе и 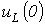на катушке индуктивности в момент коммутации в цепи на рис. 4, если .

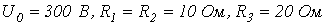Ответ:

;
.

Вау!! 😲 Ты еще не читал? Это зря!

• матричные методы расчета электрических цепей ,
• расчет нелинейных цепей методом эквивалентного генератора , методы расчета цепей постоянного тока , метод эквивалентного генератора ,
• элементы электрических цепей ,
• метод кусочно-линейной аппроксимации ,
• графические методы анализа переходных процессов , метод фазовой плоскости , метод изоклин , метод переменных состояния ,

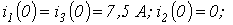
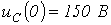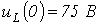Исследование, описанное в статье про переходные процессы в линейных электрических цепях с сосредоточенными параметрами, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое переходные процессы в линейных электрических цепях с сосредоточенными параметрами и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.