Однократная поперечная несимметрия в произвольной точке трехфазной системы

Привет, Вы узнаете о том , что такое однократная поперечная несимметрия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое однократная поперечная несимметрия, комплексная схема замещения , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.

Поперечная несимметрия в произвольной точке трехфазной системы в общем виде может быть представлена присоединением в этой точке трех неодинаковых сопротивлений. Такой подход позволяет получить решение в общем виде, из которого затем вытекают решения для всех частных случаев. Но такой подход приводит к громоздким выражениям, поэтому считается значительно проще и нагляднее проводить решение для каждого частного случая, используя характеризующие его граничные условия.

В этом разделе рассмотрены три основных вида несимметричных коротких замыканий (двухфазное, однофазное на землю и двухфазное на землю), наиболее часто случающиеся в системах с заземленной нейтралью. В приводимых ниже выкладках предполагается, что рассматриваются только основные гармоники тока и напряжения, причем схемы отдельных последовательностей состоят только из реактивных сопротивлений, найдены результирующая ЭДС и результирующие реактивности.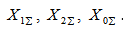

При записи граничных условий примем, что фаза «А» находится в условиях, отличных от условий для двух остальных фаз, т.е. она является, как говорят, особой фазой. За положительное направление токов будем считать направление к месту короткого замыкания.

Для упрощения записи индекс вида короткого замыкания сохранен только при записи граничных условий и в окончательных результатах.

Приняв за особую фазу «А», можно составить уравнения ЭДС и напряжений контура для соответствующих последовательностей:

(7.1)

Фазные токи и напряжения в месте короткого замыкания можно найти по формулам, полученным на основании (6.2)

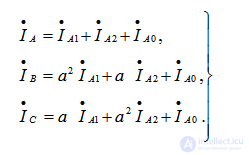(7.2)

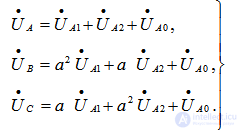(7.3)

В девяти уравнениях (7.1–7.3) имеется 12 неизвестных (). Чтобы решить эту систему уравнений, необходимо составить еще три уравнения, вытекающие из граничных условий соответствующего вида несимметричного короткого замыкания.

1. Однофазное короткое замыкание

При коротком замыкании фазы «А» на землю (рис. 7.1) граничные условия будут:

(7.4)

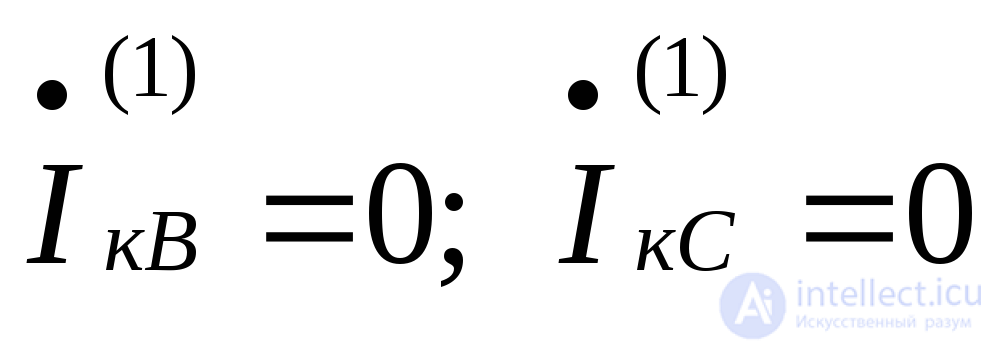(7.5)

Рис. 7.1. Однофазное короткое замыкание: а – принципиальная схема, б – векторная диаграмма напряжений в месте короткого замыкания, в – то же для токов

Вычитая третье уравнение из второго (7.2) с учетом (7.5), получим

. (7.6)

Сложив третье и второе уравнение (7.2) с учетом (7.5) и (7.6), имеем

.(7.7)

Учитывая равенство (7.7) и условие (7.4) по сумме уравнений (7.1) можно записать формулу для определения тока прямой последовательности фазы «А»:

. (7.8)

Ток в аварийной фазе

. (7.9)

Отношение тока в поврежденной фазе к току прямой последовательности называют коэффициентом взаимосвязи токов. Для однофазного короткого замыкания на землю

. (7.10)

Для начального момента короткого замыкания ток в фазе

, (7.11)

где - сверхпереходная междуфазная результирующая ЭДС.

Напряжения симметричных составляющих на основании системы уравнений (7.1.) нулевой и обратной последовательностей с учетом (7.7):

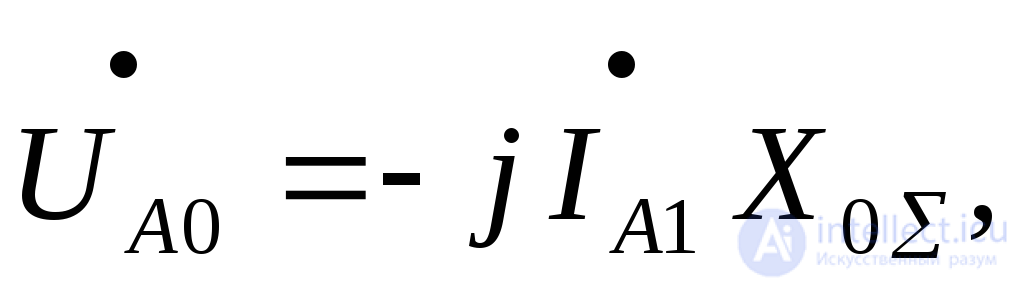(7.12)

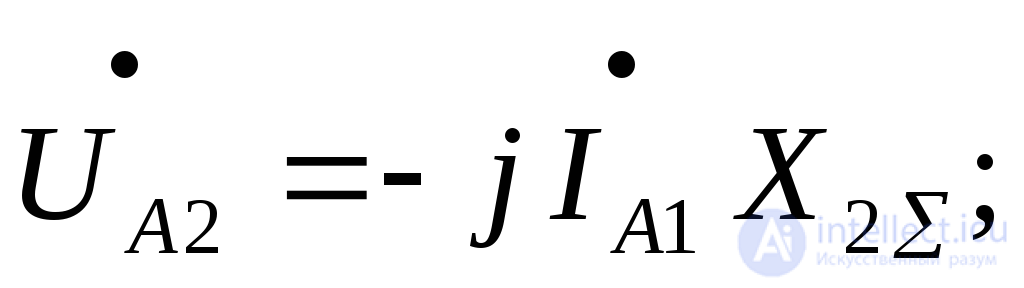(7.13)

прямой последовательности с учетом (7.4.), (7.1.), (7.13.):

(7.14)

Фазные (относительно земли) напряжения в месте короткого замыкания:

, (7.15)

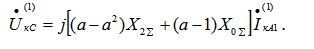. (7.16)

На рис. 7.1,б приведены векторные диаграммы напряжений и токов в месте короткого замыкания. Угол между векторами неповрежденных фаз зависит от соотношения между 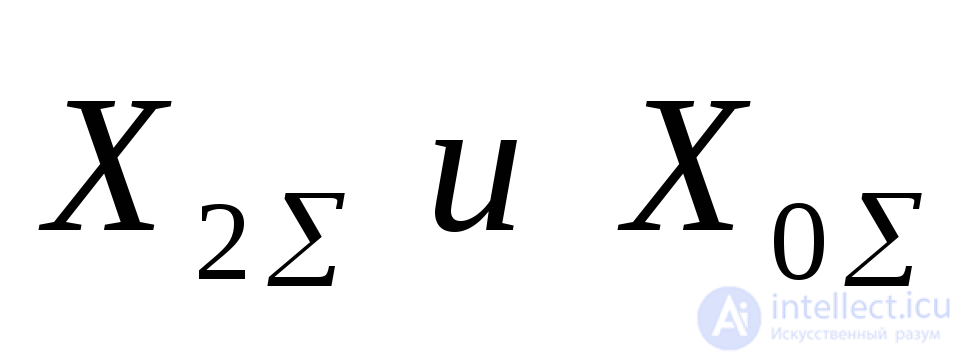. Он изменяется в широких пределах:. Приугол.

2.Двухфазное короткое замыкание

Граничные условия при замыкания фаз «В» и «С» имеют вид

, (7.17)

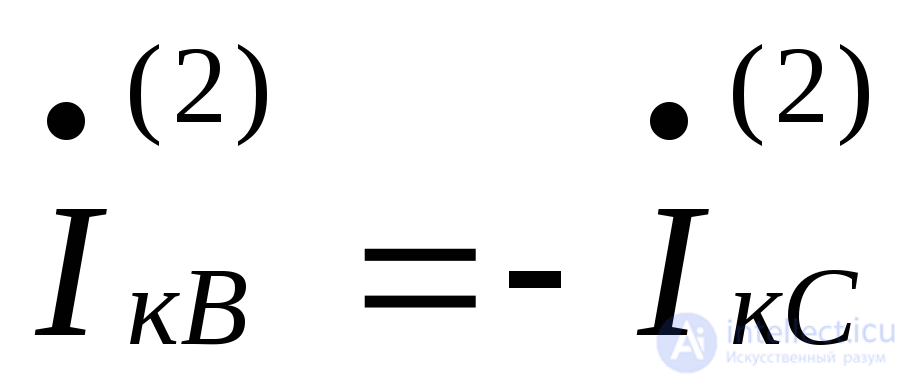, (7.18)

. (7.19)

Рис. 7.2. Двухфазное короткое замыкание: а – принципиальная схема, б – векторная диаграмма напряжений в месте короткого замыкания, в – то же для токов

Так как сумма фазных токов равна нулю, система является уравновешенной и, следовательно, . При этом согласно (7.2) ток фазы «А» будет, откуда

. (7.20)

Из условия (7.19) и (7.3)

. (7.21)

Подставив значения 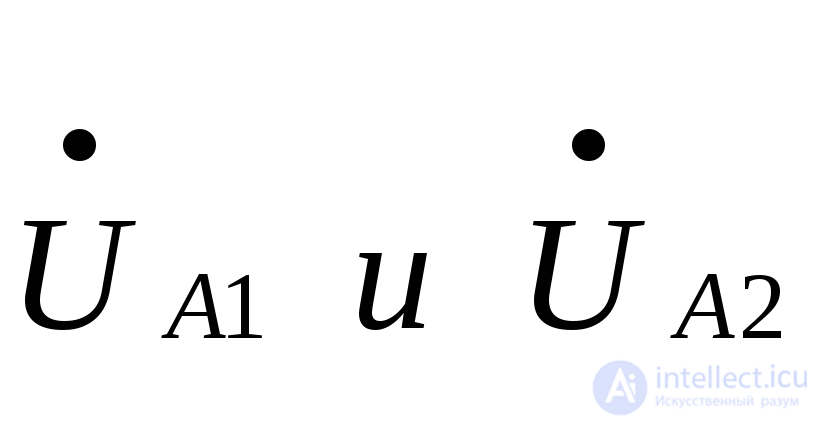, из (7.1) и (7.21) получим выражение для определения тока прямой последовательности при двухфазном коротком замыкании

. (7.22)

+Далее производя выкладки аналогично действиям в предыдущем параграфе (7.2.), определим фазные токи и напряжение, а также коэффициент взаимосвязи токов при двухфазном коротком замыкании. Полученные результаты сведены в таблицу 7.1.

3. Двухфазное короткое замыкание на землю

Двухфазное короткое замыкание на землю характеризуется граничными условиями

, (7.23)

(7.24)

Учитывая (7.23), получаем , откуда ток прямой последовательности

. (7.25)

По условиям (7.24) и используя (7.3), имеем

. (7.26)

Используя последнее равенство и уравнения (7.1), получим

, (7.27)

. (7.28)

С учетом (7.27), (7.28) по (7.25), имеем

. (7.29)

Приравняв значение по (7.1) и (7.29) можно записать

. (7.30)

Далее, действуя аналогично пункту 7.2, можно получить уравнения для вычисления фазных токов и напряжений, коэффициент взаимосвязи токов и ток в земле. Полученные результаты приведены в таблице 7.1.

Векторные диаграммы напряжений и токов в месте двухфазного короткого замыкания на землю изображены на рис. 7.3,б,в. Угол между токами поврежденных фаз может изменяться в пределах, стремясь к нижнему пределу прии к верхнему пределу при, что соответствует условиям двухфазного короткого замыкания без соединения с землей.

Рис. 7.3. Двухфазное короткое замыкание на землю: а – принципиальная схема, б – векторная диаграмма в месте короткого замыкания, в – то же для токов

4 Учет переходного сопротивления в месте замыкания

При коротких замыканиях переходное сопротивление в основном определяется сопротивлением электрической дуги, которое в первом приближении можно считать активным сопротивлением .

На рис. 7.4 приведены схемы несимметричных коротких замыканий с учетом сопротивления дуги. Здесь двухфазное короткое замыкание через дугу представлено как глухое короткое замыкание на ответвлении, фазы которого имеют одинаковое сопротивление . В схему однофазного короткого замыкания в каждую фазу введены одинаковые сопротивления. Такие искусственные приемы не нарушают граничных условий и позволяют наиболее просто получить расчетные формулы для токов и напряжений последовательностей и действительных токов и напряжений фаз по аналогии с формулами (табл. 7.1).

Для однофазного короткого замыкания через дугу формула для определения тока прямой последовательности имеет вид

(7.31)

для двухфазного короткого замыкания:

(7.32)

для двухфазного короткого замыкания на землю:

(7.33)

Рис. 7.4. Схемы несимметричных коротких замыканий через дугу для двухфазного (а), однофазного (б), двухфазного на землю (в) замыканий

5.Правило эквивалентности прямой последовательности

Структура выражений (7.8), (7.22) и (7.30) позволяет в общем виде записать ток прямой последовательности фазы «А» при любом несимметричном коротком замыкании через параметры цепи:

(7.34)

где (n) - обозначает вид короткого замыкания; - дополнительное сопротивление в зависимости от вида короткого замыкания (табл. Об этом говорит сайт https://intellect.icu . 7.1).

С учетом того, что фазные токи в месте короткого замыкания пропорциональны току прямой последовательности, модуль фазного тока в месте короткого несимметричного короткого замыкания определяется выражением

(7.35)

где m⁽ⁿ⁾ – по данным таблицы 7.1.

Обобщенная запись выражения (7.35) позволила Н. Н. Щедрину сформулировать следующее весьма важное положение.

Ток прямой последовательности любого несимметричного короткого замыкания может быть определен как ток при трехфазном коротком замыкании в точке, удаленной от действительной точки короткого замыкания на дополнительное сопротивление , которое не зависит от параметров схемы прямой последовательности и для каждого вида короткого замыкания определяется результирующими сопротивлениями обратной и нулевой последовательностей относительно рассматриваемой точки схемы, а также в общем случае сопротивлением возникшей дуги.

Это положение, которое называют правилом эквивалентности прямой последовательности, справедливо при условии, что рассматривается только основная гармоника несимметричного тока короткого замыкания.

Установленная идентичность между токами прямой последовательности несимметричного короткого замыкания и токами при некотором эквивалентном трехфазном коротком замыкании подтверждает то, что все полученные ранее выражения тока трехфазного короткого замыкания можно распространить на случай несимметричных коротких замыканий.

Правило эквивалентности прямой последовательности и установленные значения x_Δ⁽ⁿ⁾ m⁽ⁿ⁾ (см. табл. 7.1) позволяют достаточно просто сравнить различные виды короткого замыкания. Ограничимся таким сравнением для условий, когда короткозамкнутая цепь чисто индуктивная.

Полагая, что короткие замыкания различных видов происходят поочередно в одной и той же точке системы и при одних и тех же исходных условиях на основании данных таблицы 7.1 можно записать следующие неравенства:

Выясним пределы, в которых могут находиться значения токов при несимметричных коротких замыканиях по сравнению со значениями токов трехфазного короткого замыкания, возникающего в той же точке системы. Знание этих пределов представляет практический интерес, так как позволяет по известному значению тока трехфазного короткого замыкания оценить в первом приближении возможные наибольшие и наименьшие значения тока при несимметричных КЗ.

Например, при двухфазном коротком замыкании:

При КЗ вблизи зажимов генератора x_вн ≈0. При этом в начальный момент КЗ (t=0) x_1r =x_d x_2r ≈x_d. Следовательно,

X_1рез ≈ x_2рез; .

В установившемся режиме (t=∞), при котором X_1р=x_d; X_2р<<x_d; X_1рез>>x_2рез,можно полагать X_2рез≈0. Тогда Следовательно, отношениеK_(2-3) находится в следующих пределах:

Таблица 7.1. Симметричные составляющие токов и напряжений в месте коротких замыканий

№ пп	Наименование и обозначение величин	Вид короткого замыкания
		Трехфазное	Двухфазное	Однофазное	Двухфазное на землю
1	2	3	4	5	6
1	Ток прямой последовательности IA1
2	Ток обратной последовательности IA2	0	- IA1	IA1
3	Ток нулевой последовательности I0	0	0	IA1
4	Полный ток фазы: IA IВ IС	Iа1 Iа1 Iа1	0	3 IA1 0 0	0
5	Напряжение прямой последовательности UА1	0
6	Напряжение обратной последовательности UА2	0	UА1		UА1

Продолжение таблицы 7.1

1	2	3	4	5	6
7	Напряжение нулевой последовательности UА0	0	0		UА1
8	Полное фазное напряжение: UА UВ UС	0 0 0	2 UА1 -UА1 -UА1	0	3 UА1 0 0

Примечание. а = - 0,5 + j 0,866, а² = - 0,5 – j 0,866, а – а² = j , а² – а = - j .

Таблица 7.2. Значения дополнительного сопротивления и коэффициентаm⁽ⁿ⁾

Вид замыкания	(n)		m(n)
Трехфазное	(3)	0	1
Двухфазное	(2)
Однофазное	(1)		3
Двухфазное на землю	(1,1)
То же при	(1,1)

Примечание. Для упрощения записи опущен индекс у величин, которые являются соответствующими результирующими сопротивлениями относительно места короткого замыкания.

+Важно заметить, что величина тока прямой последовательности в месте короткого замыкания, а также связанные с ней величины токов других последовательностей зависят от сопротивлений всех последовательностей элементов рассматриваемой схемы (включая сопротивление дуги при ее учете). Так, например, если нейтраль трансформатора, на выводах которого имеется однофазное или двухфазное короткое замыкание на землю, заземлить через какое-либо сопротивление, то это скажется на величинах токов всех последовательностей, хотя токи прямой и обратной последовательностей через это сопротивление и не протекают.

6. Комплексные схемы замещения

На основании уравнений (7.8), (7.22) и (7.30) можно для каждого вида короткого замыкания образовать комплексные схемы замещения, соединив электрически схемы отдельных последовательностей. На рис. 7.5 приведены такие схемы, причем как общий случай здесь схема каждой последовательности характеризуется соответствующим полным сопротивлением (Z₁, Z₂, Z₀). Схемы замещения соответствуют особой фазе.

Нужно иметь в виду, что в комплексной схеме для однофазного короткого замыкания (рис.7.5) обеспечиваются правильные значения напряжений прямой последовательности в различных точках. Что касается обратной и нулевой последовательностей, то они должны определяться относительно точек нулевого потенциала схем одноименных последовательностей, т.е. соответственно по отношению к точкам Н₂ и Н₀, которые являются началами схем этих последовательностей.

Сравнения видов короткого замыкания

Правило эквивалентности прямой последовательности и установленные значения 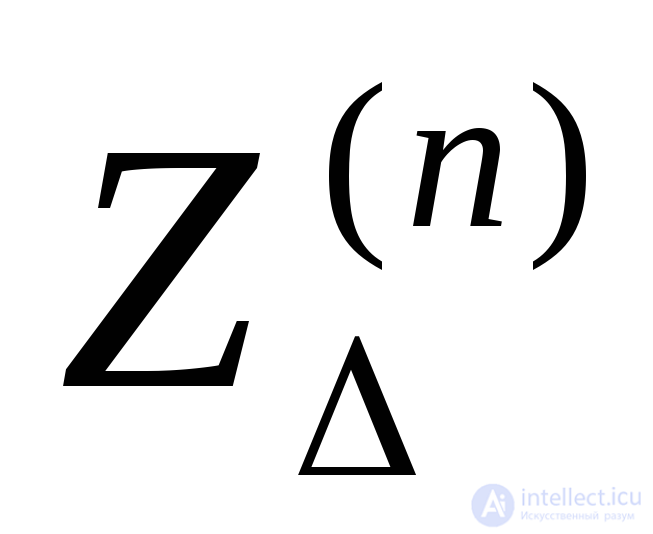и(табл. 7.2) позволяют достаточно просто сравнить различные виды короткого замыкания.

Имея в виду, что короткие замыкания происходят поочередно в одной и той же точке системы и при одних и тех же исходных условиях, на основании таблицы 7.2 можно написать, что между величинами дополнительных реактивных сопротивлений при различных видах короткого замыкания существуют неравенства

.

Соответственно

и .

Рис. 7.5. Комплексные схемы замещения: а – для двухфазного замыкания, б – для однофазного замыкания, в – для двухфазного замыкания на землю

Рис. 7.6. Эпюры относительных напряжений отдельных последовательностей: а – принципиальная схема, б – двухфазное замыкание, в – однофазное замыкание, г – двухфазное замыкание на землю

7. Применение практических методов к расчету переходного процесса при однократной поперечной несимметрии

Все изложенные ранее практические методы и приемы расчета переходного процесса при трехфазном коротком замыкании согласно правилу эквивалентности прямой последовательности могут быть применены для расчета переходного процесса при любом несимметричном коротком замыкании. В большинстве практических расчетов начального момента несимметричного переходного процесса в качестве обратной последовательности можно принимать схему прямой последовательности, исключив из нее все ЭДС; при этом можно полагать, что .

Поскольку напряжение прямой последовательности в любой точке схемы при несимметричном коротком замыкании всегда выше, чем при трехфазном коротком замыкании в той же точке, то подпитывающий эффект отдельных двигателей или нагрузки в целом при несимметричных коротких замыканиях проявляется слабее, чем при трехфазном коротком замыкании. Поэтому при расчете ударного тока несимметричного короткого замыкания часто можно пренебрегать нагрузками и отдельными двигателями, за исключением лишь достаточно мощных двигателей, непосредственно связанных с точкой короткого замыкания.

При необходимости более точного учета нагрузки, что встречается при определении токораспределения (главным образом для целей релейной защиты), удобно использовать принцип наложения предшествующего нормального режима на собственно аварийный режим. Расчет последнего при несимметричном коротком замыкании сводится к нахождению токов и напряжений в соответствующей данной несимметрии комплексной схеме при включении ее на напряжение, равное по величине и противоположное по направлению тому напряжению, которое было в точке короткого замыкания до его возникновения. Дополнительное упрощение в расчете такого режима, как известно, состоит в пренебрежении активными сопротивлениями элементов схемы. Однако в протяженной воздушной и особенно кабельной сети часто приходится учитывать активное сопротивление линий, влияние которого особенно заметно при однофазном коротком замыкании. То же самое надо сказать и об учете токоограничивающего эффекта дуги, возникающей в месте короткого замыкания.

Пример 7.1. Оценить степень участия нагрузок в начальном сверхпереходном токе при двухфазном коротком замыкании в точке К и сравнить ее, если в той же точке произойдет трехфазное короткое замыкание.

К примеру 7.7:

а – исходная схема,

б – схема замещения прямой последовательности

Исходные данные:

С – система,

Р – реактор сдвоенный 2*1000 А, 6 кВ,

х = 8 %, коэффициент связи 0,46.

Т – трансформатор 60 МВА, 115/6,3 кВ,

U_к= 10,5 %

Н-1, Н-2 нагрузки по 17,5 МВА,

Н-3, Н-4 нагрузки по 8 МВА.

На рис. 7.7,б приведена схема замещения прямой последовательности, где все элементы и ЭДС выражены в относительных единицах при .

Схема обратной последовательности в данном случае будет такой же, за исключением того, что в ней все ЭДС будут равны нулю.

Произведем преобразование схемы к элементарному виду:

При двухфазном коротком замыкании ток прямой последовательности в месте короткого замыкания составляет

а напряжение прямой последовательности в месте короткого замыкания

Ток прямой последовательности в элементе 4:

.

Напряжение прямой последовательности за этим элементом:

.

Ток прямой последовательности, поступающий в нагрузку (элемент 9):

.

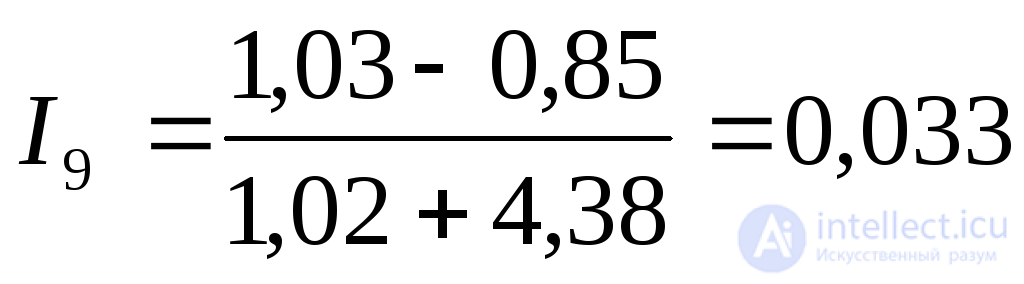Напряжение прямой последовательности на шинах подстанции:

.

Следовательно, нагрузки H-1 и Н-2 в схеме прямой последовательности никакого участия не принимают, так как ток этой последовательности в них отсутствует. Наличие нагрузок сказывается лишь в очень незначительном снижении результирующей реактивности .

Начальный сверхпереходный ток в месте двухфазного короткого замыкания будет:

или

.

При этом , если исключить нагрузку Н-3, этот ток был бы:

,

т.е. подпитка от нагрузки Н-3 составляет

Аналогичный расчет для трехфазного короткого замыкания в той же точке показывает, что остаточное напряжение на шинах подстанции снижается до U= 0,73 и участие нагрузок в образовании сверхпереходного начального тока в месте короткого замыкания составляет приблизительно 25 %.

Пример 7.2. При включении асинхронного двигателя М, питающегося от шин 6 кВ понижающей подстанции (рис. 7.8,а) одна фаза из-за неисправности выключателя Q осталась разомкнутой. Для этих условий определить величину начального пускового тока и оценить в какой мере это отразится на вращающемся моменте других асинхронных двигателей, которые питаются от тех же шин.

Система характеризуется неизменным напряжением 115 кВ, приложенным за реактивным сопротивлением

х₁= х₂=26,4 Ом.

Трансформатор: Т 10 МВА, 115/6,3 кВ, U_к= 10 %.

Асинхронный двигатель М 4000 кВт, 6кВ, , к.п.д. =0,92,I_пуск= 4,5. Нагрузка Н 2,5 МВА.

Рис. 7.8. К примеру 7.2:

а – исходная схема, б – комплексная схема замещения

Пуск двигателя на двух фазах можно рассматривать как двухфазное короткое замыкание за реактивным сопротивлением заторможенного двигателя, которое в прямой и обратной последовательностях одинакова. Таким образом, для заданных условий комплексная схема имеет вид, представленный на рис. 7.8,б, гдеN₁иN₂– нейтральные точки обмотки статора двигателя соответственно в схемах прямой и обратной последовательностей. Указанные на схеме величины реактивных сопротивлений и ЭДС в относительных единицах при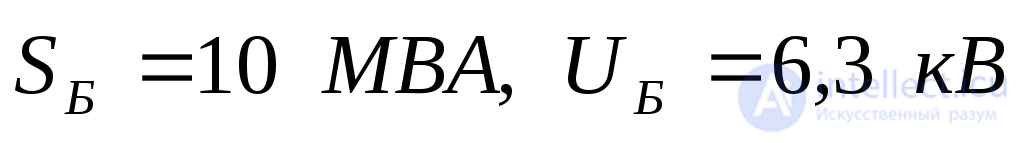. Соответственно.

Решение:

Номинальная полная мощность двигателя:

.

Реактивное сопротивление двигателя при базисных условиях:

.

Результирующие реактивности относительно точек N₁иN₂:

.

Результирующая ЭДС

.

Составляющая прямой последовательности пускового тока:

а величина пускового тока при базисных условиях

и при номинальных условиях двигателя

т.е. он меньше номинального пускового тока на .

Симметричные составляющие напряжения на шинах:

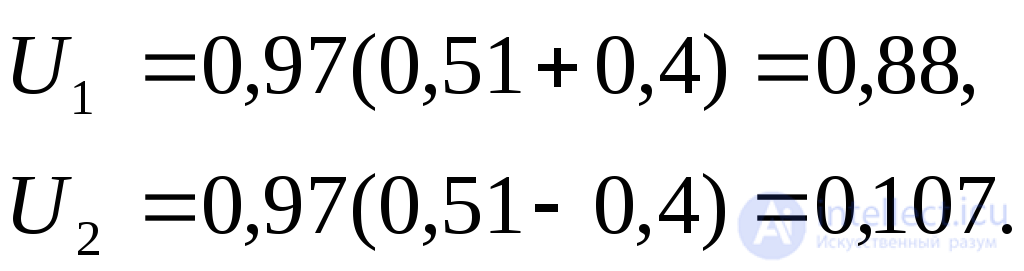
Имея в виду, что момент от напряжения обратной последовательности при рабочем скольжении ничтожно мал, вращающий момент двигателей, питающихся от шин по трем фазам, практически будет:

,

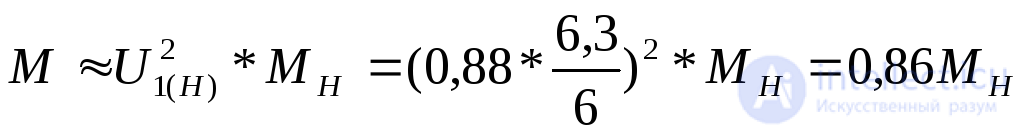т.е. снизится на 14 %.

Что касается двигателя, включенного двумя фазами, то на его выводах составляющие напряжения будут:

и пусковой момент двигателя, как и следовало ожидать, М_пуск= 0.

Пример 7.3. На линии схемы (рис. 7.9) произошло металлическое замыкание между фазами «В» и «С» с одновременным замыканием общей точки через дугу на землю. Определить токи и напряжения в начале линии для начального нарушения режима.

Генератор G 60 МВА; 10,5 KB; предварительно работал на холостом ходу с номинальным напряжением.

Трансформатор Т 60 МВА; 154/10,5 кB; Uк =10 %.

Линия Л .

Сопротивление дуги r_g = 9,5 Ом.

Примем за базисные условия . Тогда сопротивления линии в относительных базисных единицах будут:

и сопротивление дуги: r_g = 0,04.

На рис. 7.9 приведена комплексная схема замещения для рассматриваемого случая. Результирующие сопротивления схем отдельных последовательностей составляют:

Рис. 7.9. К примеру 7.3

Дополнительное сопротивление:

.

Суммарное сопротивление для данного вида замыкания:

.

Симметричные составляющие токов в месте короткого замыкания (они же в данном случае являются симметричными составляющими фазных токов линии)

Симметричные составляющие напряжений в начале линии здесь легче определить, идя в схеме каждой последовательности от точки нулевого потенциала, т.е.

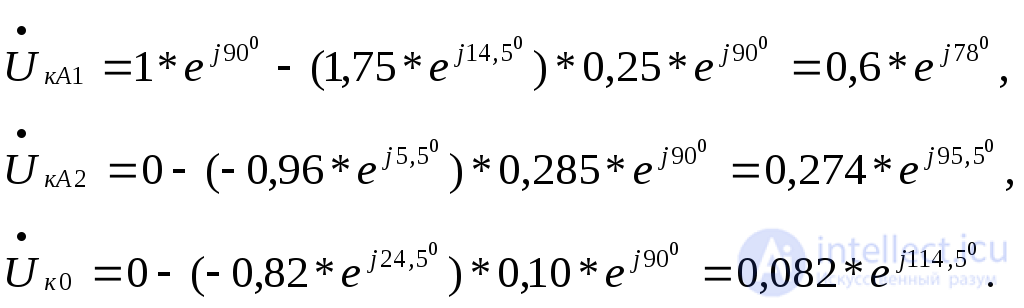
По найденным симметричным составляющим токов и напряжений получить значения фазных токов и напряжений уже не представляет большого труда либо с помощью векторной диаграммы, либо аналитически.

Исследование, описанное в статье про однократная поперечная несимметрия, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое однократная поперечная несимметрия, комплексная схема замещения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники