29. Интеграл Дюамеля. Метод переменных состояния кратко

Привет, Вы узнаете о том , что такое интеграл дюамеля, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое интеграл дюамеля, метод переменных состояния , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.

Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 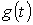или (и) переходную функцию по напряжению , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , а вторую - как t.

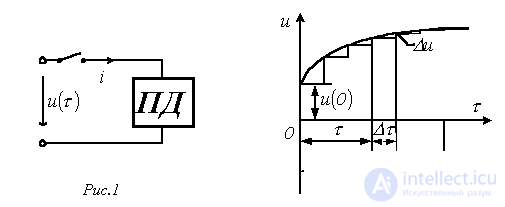
Пусть в момент времени к цепи с нулевыми начальными условиями (пассивному двухполюснику ПД на рис. 1) подключается источник с напряжением 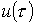произвольной формы. Для нахождения тока в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения 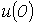и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.

В момент времени t составляющая общего тока, определяемая начальным скачком напряжения , равна .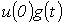

В момент времени 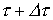имеет место скачок напряжения 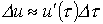, который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .

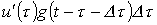Полный ток 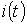в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом 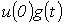, т.е.

.

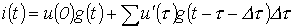Заменяя конечный интервал приращения времени 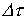на бесконечно малый, т.е. переходя от суммы к интегралу, запишем

.

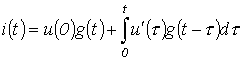(1)

Соотношение (1) называется интегралом Дюамеля.

Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости 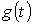будет входить переходная функция по напряжению.

Последовательность расчета с использованием
интеграла Дюамеля

1. Определение функции (или ) для исследуемой цепи.
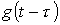2. Запись выражения (или 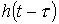) путем формальной замены t на .
3. Определение производной .
4. Подстановка найденных функций в (1) и интегрирование определенного интеграла.

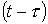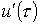В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.

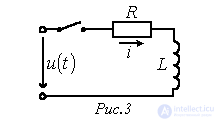
Исходные данные для расчета: , , .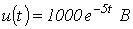

.

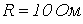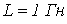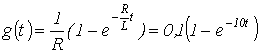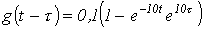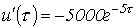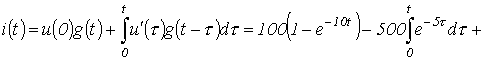
1. Переходная проводимость
2. .
3. .
4. 

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.

метод переменных состояния

Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.

Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. Об этом говорит сайт https://intellect.icu . записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.

Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.

К уравнениям состояния выдвигаются два основных требования:

-независимость уравнений;

-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.

Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.

Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.

При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные и 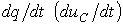с самими переменным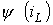и и 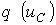и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.

Таким образом, полная система уравнений в матричной форме записи имеет вид

;

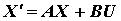(2)

.

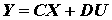(3)

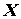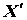Здесь и - столбцовые матрицы соответственно переменных состояния и их первых производных по времени; 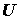- матрица-столбец источников внешних воздействий; - столбцовая матрица выходных (искомых) величин; - квадратная размерностью n x n (где n – число переменных состояния) матрица параметров, называемая матрицей Якоби; 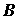- прямоугольная матрица связи между источниками и переменными состояния (количество строк равно n, а столбцов – числу источников m); 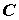- прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); 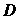- прямоугольная размерностью к x mматрица связи входа с выходом.

Начальные условия для уравнения (2) задаются вектором начальных значений 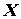(0).

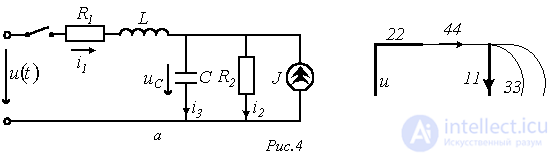
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить ток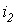и и .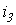

По законам Кирхгофа для данной цепи запишем

;

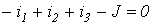(4)

;

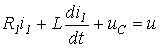(5)

.

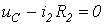(6)

Поскольку с учетом соотношения (6) перепишем уравнения (4) и (5) в виде

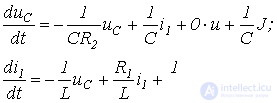
или в матричной форме записи

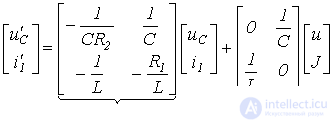
А

В

Матричное уравнение вида (3) вытекает из соотношений (4) и (6):

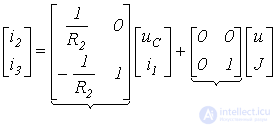
С

D

Вектор начальных значений 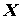(0)= .

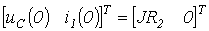Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.

Методика составления уравнений состояния

Эта методика включает в себя следующие основные этапы:

1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.

2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).

3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.

Таблица 1. Таблица соединений

	11	22	u
33	-1	0	0
44	1	1	1
J	1	0

Процедура заполнения таблицы заключается в поочередном мысленном замыкании ветвей дерева с помощью ветвей связи до получения контура с последующим обходом последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются ветви графа, ориентация которых совпадает с направлением обхода контура, и со знаком «-» ветви, имеющие противоположную ориентацию.

Осуществляется расписывание таблицы по столбцам и по строкам. В первом случае получаются уравнения по первому закону Кирхгофа, во втором – по второму.

В рассматриваемом случае (равенство 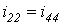тривиально)

,

откуда в соответствии с нумерацией токов в исходной цепи

.

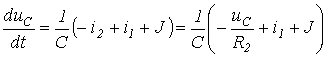При расписывании таблицы соединений по строкам напряжения на пассивных элементах необходимо брать со знаками, противоположными табличным:

(7)

Эти уравнения совпадают соответственно с соотношениями (6) и (5).

Из (7) непосредственно вытекает

.

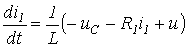Таким образом, формализованным способом получены уравнения, аналогичные составленным выше с использованием законов Кирхгофа.

Литература

1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. радиотехн. спец. вузов. 3-е изд., перераб. и доп. –М.: Высш. шк., 1990. –400с.

Контрольные вопросы и задачи

Ответ: 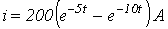при ; при .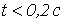

1. Какой принцип лежит в основе метода расчета переходных процессов с использованием интеграла Дюамеля, и для каких цепей может быть использован данный метод?
2. В каких случаях целесообразно использовать метод расчета с использованием интеграла Дюамеля?
3. В цепи на рис. 3 при 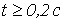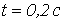напряжение на входе цепи мгновенно спадает до нуля. Определить ток в цепи.
4. Какие требования и почему выдвигаются к уравнениям состояния?
5. Что включает в себя система уравнений при расчете переходного процесса в цепи методом переменных состояния?
6. Перечислите основные этапы методики составления уравнений состояния.
7. Записать матрицы А и В для цепи на рис. 5, если , , , , , .

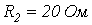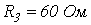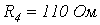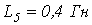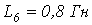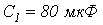Ответ:

А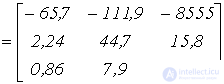
В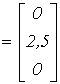

Исследование, описанное в статье про интеграл дюамеля, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое интеграл дюамеля, метод переменных состояния и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники

Из статьи мы узнали кратко, но содержательно про интеграл дюамеля

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.