Лекция
Привет, Вы узнаете о том , что такое метод кусочно-линейной аппроксимации, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод кусочно-линейной аппроксимации , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
В соответствии с определением данного метода, расчет нелинейной цепи с его использованием включает в себя в общем случае следующие основные этапы:
1. Исходная характеристика нелинейного элемента заменяется ломаной линией с конечным числом прямолинейных отрезков.
2. Для каждого участка ломаной определяются эквивалентные линейные параметры нелинейного элемента и рисуются соответствующие линейные схемы замещения исходной цепи.
3. Решается линейная задача для каждого отрезка в отдельности.
4. На основании граничных условий определяются временные интервалы движения изображающей точки по каждому прямолинейному участку (границы существования отдельных решений).
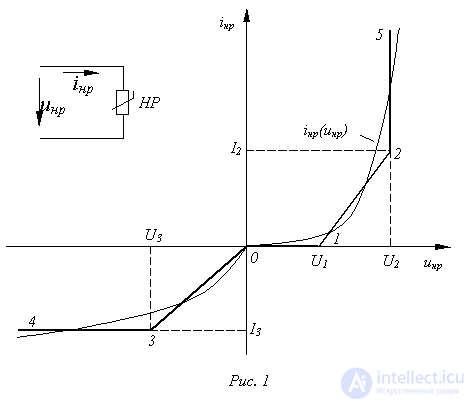
Пусть вольт-амперная харак-теристика (ВАХ) нелинейного резистора имеет форму, представленную на рис. 1. Заменяя ее ломаной линией 4-3-0-1-2-5, получаем приведенные в табл. 1 расчетные эквивалентные схемы замещения и соответ-ствующие им линейные соотношения.
Расчет каждой из полученных линейных схем замещения при наличии в цепи одного нелинейного элемента и произвольного числа
линейных не представляет труда. В этом случае на основании теоремы об активном двухполюснике исходная нелинейная цепь сначала сводится к схеме, содержащей эквивалентный генератор с некоторым линейным внутренним сопротивлением и последовательно с ним включенный нелинейный элемент, после чего производится ее расчет. При наличии в цепи переменного источника энергии рабочая (изображающая) точка будет постоянно скользить по аппроксимирующей характеристике, переходя через точки излома. Переход через такие точки соответствует мгновенному изменению схемы замещения. Поэтому задача определения искомой переменной сводится не только к расчету схем замещения, но и к определению моментов “переключения” между ними, т.е. нахождению граничных условий по времени. Анализ существенно усложняется, если в цепи имеется несколько нелинейных элементов. Главная трудность в этом случае связана с тем, что заранее не известно сочетание линейных участков, соответствующее заданному входному напряжению (току). Искомое сочетание линейных участков всех нелинейных элементов определяется перебором их возможных сочетаний. Для любого принятого сочетания параметры схемы известны, и, следовательно, могут быть определены напряжения и токи для всех элементов. Если они лежат в пределах соответствующих линейных участков, то принятое сочетание дает верный результат. Если хотя бы у одного нелинейного элемента переменные выходят за границы рассматриваемого линейного участка, то следует перейти к другому сочетанию.
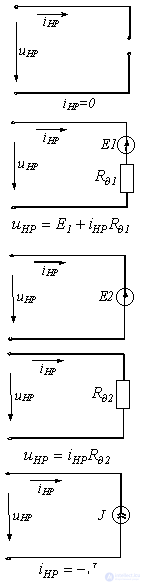
Таблица 1. Кусочно-линейная аппроксимация ВАХ нелинейного резистора
|
Участок кривой |
Схема замещения |
Параметры элементов |
Граничные условия |
|||||
|
 |
 |
|
Необходимо отметить, что всегда имеется единственное сочетание линейных участков характеристик нелинейных элементов, соответствующее изменению входного сигнала в некоторых пределах.
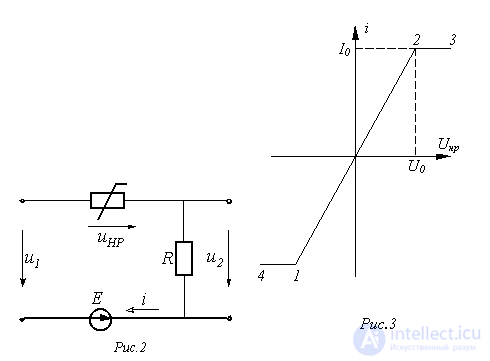
В качестве примера определим напряжение 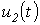 в цепи на рис. 2, в которой
в цепи на рис. 2, в которой 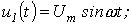
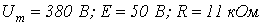 . ВАХ нелинейного резистора приведена на рис. 3, где
. ВАХ нелинейного резистора приведена на рис. 3, где 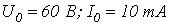 .
.
Решение
1. В соответствии с заданной ВАХ нелинейный резистор на участке 1-2 заменяем линейным резистором с сопротивлением
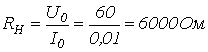 ,
,
на участке 2-3-источником тока с током 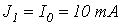 и на участке 4-1-источником тока с током
и на участке 4-1-источником тока с током 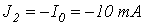 .
.
2. Об этом говорит сайт https://intellect.icu . На основании данной эквивалентной замены для тока на участке 1-2 ВАХ можно записать:
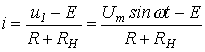 |
(1) |
откуда
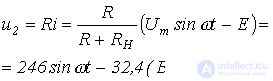
При движении изображающей точки по участку 2-3 ВАХ имеем
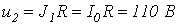 ,
,
при движении по участку 1-4 ВАХ-
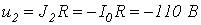 .
.
3. Определяем интервалы движения изображающей точки по отдельным участкам ВАХ. Для точки излома 1 на основании (1) справедливо уравнение
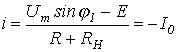
или
 .
.
Отсюда получаем два значения мгновенной фазы питающего напряжения на одном периоде, соответствующих точке 1: 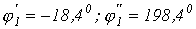 . Первое значение определяет переход изображающей точки с участка 4-1 на участок 1-2, второе – с участка 2-1 на участок 1-4.
. Первое значение определяет переход изображающей точки с участка 4-1 на участок 1-2, второе – с участка 2-1 на участок 1-4.
Аналогично записываем для точки 2 излома ВАХ

или
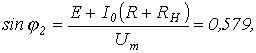
откуда  (значение, соответствующее переходу с участка 1-2 на участок 2-3) и
(значение, соответствующее переходу с участка 1-2 на участок 2-3) и 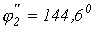 (значение, соответствующее переходу с участка 3-2 на участок 2-1).
(значение, соответствующее переходу с участка 3-2 на участок 2-1).
Таким образом, получаем для одного периода питающего напряжения

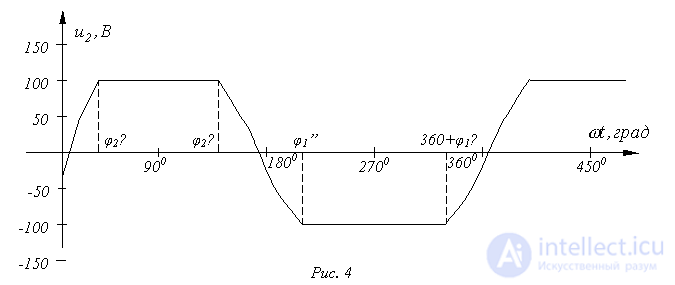
В соответствии с периодичностью синусоидальной функции данные решения повторяются через 360°n.
На рис. 4 представлен график зависимости искомой величины.
Применение аналитического выражения для аппроксимации характеристики нелинейного элемента позволяет наименее трудоемко провести расчет, когда закон изменения во времени одной из переменных, определяющих работу нелинейного элемента (ток или напряжение для резистора, потокосцепление или ток для катушки индуктивности, заряд или напряжение для конденсатора), задан или вытекает из предварительного анализа физических условий протекания процесса, что имело место при решении предыдущих задач данного раздела. Если такая определенность отсутствует, то задачу в общем случае можно решить только приближенно. Одним из таких методов, наиболее широко применимым на практике, является метод гармонического баланса.
Метод основан на разложении периодических функций в ряд Фурье. В общем случае искомые переменные в нелинейной электрической цепи несинусоидальны и содержат бесконечный спектр гармоник. Ожидаемое решение можно представить в виде суммы основной и нескольких высших гармоник, у которых неизвестными являются амплитуды и начальные фазы. Подставляя эту сумму в нелинейное дифференциальное уравнение, записанное для искомой величины, и приравнивая в полученном выражении коэффициенты перед гармониками (синусоидальными и косинусоидальными функциями) одинаковых частот в его левой и правой частях, приходим к системе из 2n алгебраических уравнений, где n-количество учтенных гармоник. Необходимо отметить, что точное решение требует учета бесконечного числа гармоник, что невозможно осуществить практически. В результате ограничения числа рассматриваемых гармоник точный баланс нарушается, и решение становится приближенным.
Методика расчета нелинейной цепи данным способом включает в себя в общем случае следующие основные этапы:
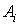 и начальными фазами
и начальными фазами 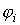 .
. и начальных фаз
и начальных фаз  функции разложения определяемой величины.
функции разложения определяемой величины.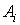 и
и 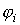 .
.Частным случаем метода гармонического баланса является метод расчета по первым гармоникам несинусоидальных величин (метод гармонической линеаризации), когда высшими гармониками искомых переменных, а также входных воздействий пренебрегают. При анализе используется характеристика нелинейного элемента по первым гармоникам, для получения которой в аналитическое выражение нелинейной характеристики для мгновенных значений подставляется первая гармоника одной из двух переменных, определяющих эту характеристику, и находится нелинейная связь между амплитудами первых гармоник этих переменных. Этапы расчета соответствуют изложенным для метода гармонического баланса. При этом, в силу того, что конечная система нелинейных уравнений имеет второй порядок, в ряде случаев появляется возможность их аналитического решения. Кроме того, поскольку рассматриваются только первые гармоники несинусоидальных величин, при расчете можно использовать символический метод.
Пусть, например, в цепи, питаемой от источника синусоидального напряжения 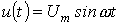 и состоящей из последовательно соединенных линейного резистора
и состоящей из последовательно соединенных линейного резистора  и нелинейной катушки, вебер-амперная характеристика которой задана аппроксимацией вида
и нелинейной катушки, вебер-амперная характеристика которой задана аппроксимацией вида  , необходимо определить первую гармонику тока, задаваемую выражением
, необходимо определить первую гармонику тока, задаваемую выражением 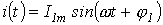 , где
, где 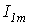 и
и 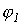 - неизвестные (искомые величины).
- неизвестные (искомые величины).
Для решения определяем аналитическое выражение характеристики 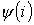 для первых гармоник:
для первых гармоник:

откуда
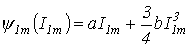 . . |
(2) |
После подстановки выражения тока и соотношения (2) в уравнение состояния цепи
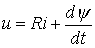
получаем
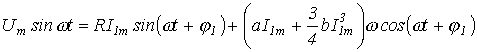
или
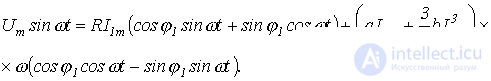
На основании последнего получаем систему уравнений
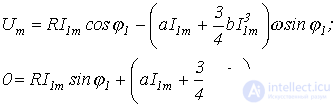
из которых находим искомые параметры 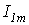 и
и 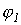 .
.
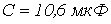 и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением
и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением 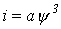 , где
, где 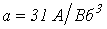 , питаются от источника синусоидального напряжения
, питаются от источника синусоидального напряжения 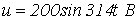 . Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
. Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.Ответ: 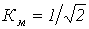 .
.
Ответ:  .
.
Исследование, описанное в статье про метод кусочно-линейной аппроксимации, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое метод кусочно-линейной аппроксимации и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Из статьи мы узнали кратко, но содержательно про метод кусочно-линейной аппроксимацииОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники