Лекция
Привет, Вы узнаете о том , что такое векторные диаграммы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое векторные диаграммы, топографические диаграммы , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы.
При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию № 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях.
Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы . Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1).
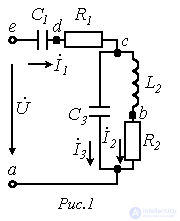
Параметры схемы: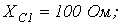 
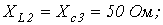
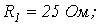
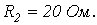
При данных параметрах и заданном напряжении на входе схемы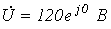 
найденные значения токов (см. лекцию № 5) равны: 
; 
; 
.
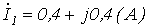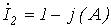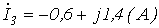При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рис. 2). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы . Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней.
Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов (другой вариант построения топографической диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим суммированием векторов напряжений вдоль контура непосредственно на комплексной плоскости).
При построении топографической диаграммы обход контуров можно производить по направлению тока или против. Чаще используют второй вариант.
В этом случае с учетом того, что в электротехнике принято, что ток течет от большего потенциала к меньшему, потенциал искомой точки равен потенциалу предыдущей плюс падение напряжения на элементе между этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает. Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное ЭДС.
Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал точки а за нуль(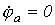 
), определим потенциалы этих точек:
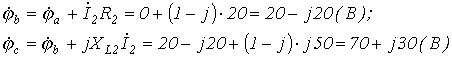
или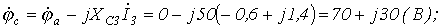 
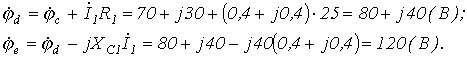
Таким образом, в результате проведенных вычислений получено, что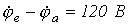 
. Но разность потенциалов точек е и а равно напряжению U, приложенному к цепи, а оно равно 120 В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления выполнены верно. Об этом говорит сайт https://intellect.icu . В соответствии с полученными результатами строится топографическая диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих топографическую диаграмму, относительно векторов тока: для резистивных элементов соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.
В заключение заметим, что векторы напряжений ориентированы относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек электрической цепи. В этой связи допускается не указывать на топографической диаграмме направления векторов напряжений.
Потенциальная диаграмма
Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме.
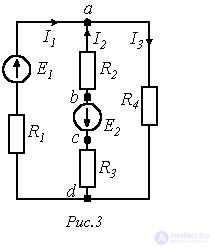
Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3.
При параметрах схемы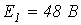 
; 
; 
; 
; 
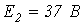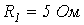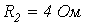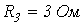и 
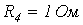токи в ветвях схемы равны: 
; 
; 
.
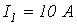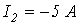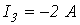Построим потенциальную диаграмму для контура abcda.
Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль рассматриваемого контура: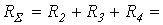 
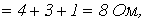после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a, потенциал которой принят за нуль:
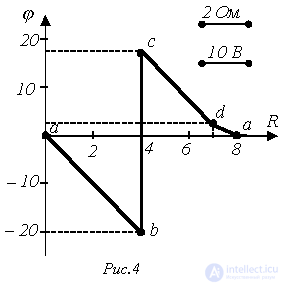
Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20); c(4;17); d(7;2). С учетом выбранных масштабов на рис. 4 построена потенциальная диаграмма для выбранного контура.
Преобразование линейных электрических схем
Для упрощения расчета и повышения наглядности анализа сложных электрических цепей во многих случаях рационально подвергнуть их предварительному преобразованию. Очевидно, что преобразование должно приводить к упрощению исходной схемы за счет уменьшения числа ее ветвей и (или) узлов. Такое преобразование называется целесообразным. При этом при любых способах преобразований должно выполняться условие неизменности токов в ветвях участков схемы, не затронутых этими преобразованиями. Из последнего вытекает, что, если преобразованию подвергаются участки цепи, не содержащие источников энергии, то мощности в исходной и эквивалентной схемах одинаковы. Если в преобразуемые участки входят источники энергии, то в общем случае мощности в исходной и преобразованной цепях будут различны.
Рассмотрим наиболее важные случаи преобразования электрических цепей.
1. Преобразование последовательно соединенных элементов
Рассмотрим участок цепи на рис. 5,а. При расчете внешней по отношению к этому участку цепи данную ветвь можно свести к виду на рис. 5,б, где
 |
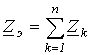(1) |
или
 . |
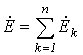(2) |
При этом при вычислении эквивалентной ЭДС 
k-я ЭДС берется со знаком “+”, если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если не совпадает.
2. Преобразование параллельно соединенных ветвей
Пусть имеем схему на рис. 6,а.
Согласно закону Ома для участка цепи с источником ЭДС
,
где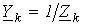 
.
Тогда
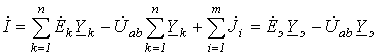,где
 ; |
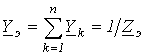(3) |
 , |
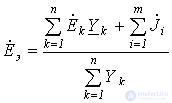(4) |
причем со знаком “+” в (4) записываются ЭДС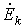 
и ток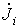 
, если они направлены к тому же узлу, что и ЭДС 
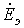; в противном случае они записываются со знаком “-”.
3. Взаимные преобразования “треугольник-звезда”
В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.
Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными.
Без вывода запишем формулы эквивалентных преобразований
|
Треугольник |
Звезда |
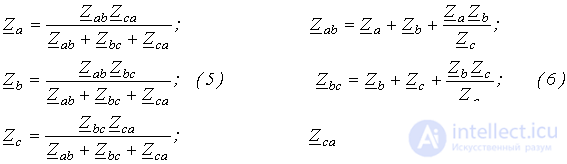
Литература
Контрольные вопросы и задачи
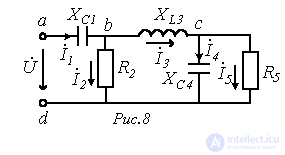
Ответ: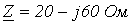 
.
Ответ: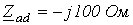 
; 
; 
.
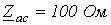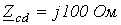Ответ: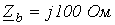 
; 
; 
.
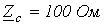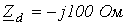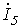и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее.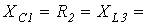
.
, 
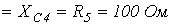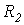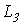и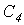 
.Исследование, описанное в статье про векторные диаграммы, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое векторные диаграммы, топографические диаграммы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Из статьи мы узнали кратко, но содержательно про векторные диаграммыОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
звезда
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники