Лекция
Привет, Вы узнаете о том , что такое теория атома, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теория атома , настоятельно рекомендую прочитать все из категории Атомная и Ядерная физика.
Раз уж мы получили в руки такое мощное оружие, как уравнение Шредингера, то естественно вернуться к атому, начав с простейшего — атома водорода. Надо же убедиться, что квантовая механика приведет к тем же результатам, что и полуклассическая теория атома по Бору. К тому же есть надежда, что новая теория подарит нам неожиданные открытия. Жаль только, что изучение способов решения уравнения Шредингера не входит в рамки настоящего курса. Но не беда: мы постараемся обойтись без излишней математики, угадывая свойства решений на основе интуиции, выработанной при изучении классической физики. При этом, конечно, читателя никто обманывать не собирается: все «угаданное» может быть получено из уравнения Шредингера точными математическими расчетами.

Рис. 5.1. Физики, внесшие большой вклад в развитие квантовой механики на ее раннем этапе: (слева направо) Нильс Бор, Альберт Эйнштейн, Макс Планк, Вольфганг Паули, Вернер Гейзенберг, Эрвин Шредингер
В предыдущей главе мы установили, что классические динамические переменные заменяются в квантовой механике на операторы, действующие на волновую функцию. Результатами измерения некой величины А всегда будут собственные значения 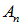 соответствующего оператора
соответствующего оператора
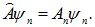
Если система находится в каком-нибудь собственном состоянии 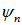 оператора
оператора 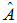 , то измерение наверняка дает собственное значение
, то измерение наверняка дает собственное значение 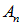 . Если же система находится в каком-то другом состоянии, то измерение величины А с определенной вероятностью дает какое-то из собственных значений, причем эта вероятность зависит от волновой функции состояния и, разумеется, от измеряемой величины А.
. Если же система находится в каком-то другом состоянии, то измерение величины А с определенной вероятностью дает какое-то из собственных значений, причем эта вероятность зависит от волновой функции состояния и, разумеется, от измеряемой величины А.
Пусть система находится в состоянии с определенным значением величины А. Это значит, что ее волновая функция является собственной функцией оператора 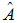 . Может ли другая величина В также иметь определенное значение? Иначе, может ли состояние быть собственным сразу и для оператора
. Может ли другая величина В также иметь определенное значение? Иначе, может ли состояние быть собственным сразу и для оператора 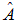 , и для
, и для 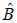 ?
?
Правило 3
|
Два оператора
|
Иначе: если результат последовательного действия двух операторов не зависит от порядка их применения, то соответствующие величины могут одновременно иметь определенные значения.
Рассмотрим пример
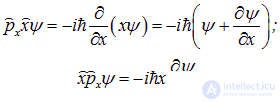
то есть для любой функции 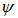
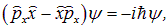
или просто
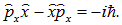
|
Поскольку операторы |
Этот вывод и есть истинный источник соотношений неопределенностей Гейзенберга, физический смысл которых разобран выше.
Особое значение имеет свойство коммутации операторов с гамильтонианом, то есть с оператором полной энергии 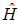 . Если какой-то оператор
. Если какой-то оператор 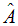 коммутирует с
коммутирует с 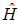 , то существует общее собственное состояние, которое стационарно по определению. В стационарном же состоянии система пребывает неограниченно долго. Это означает одновременно и сохранение величины А. Таким образом, утверждение о сохранении некой величины эквивалентно тому, что она может иметь определенное значение вместе с энергией, то есть соответствующий ей оператор коммутирует с гамильтонианом.
, то существует общее собственное состояние, которое стационарно по определению. В стационарном же состоянии система пребывает неограниченно долго. Это означает одновременно и сохранение величины А. Таким образом, утверждение о сохранении некой величины эквивалентно тому, что она может иметь определенное значение вместе с энергией, то есть соответствующий ей оператор коммутирует с гамильтонианом.
В классической механике момент импульса частицы (его также называют моментом количества движения или угловым моментом) выражается в виде векторного произведения радиуса-вектора на импульс частицы:
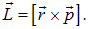
То же соотношение верно для операторов в квантовой механике:
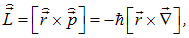
или по компонентам
|
|
|
(5.1) |
и аналогично для других компонент
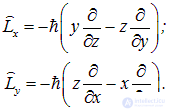
Ранее обсуждалось, почему оператор проекции момента количества движения на какую-то ось связан с производной по углу поворота вокруг этой оси (см. уравнение (4.16)). В сферических координатах поворот вокруг оси z эквивалентен сдвигу по азимутальному углу 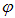 , и потому оператор (4.1) имеет особенно простой вид
, и потому оператор (4.1) имеет особенно простой вид
|
|
|
(5.2) |
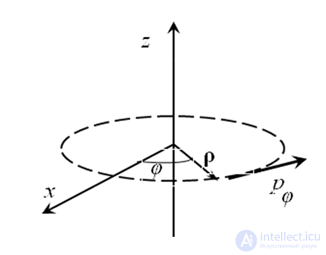
Рис. 5.2. Проекция момента импульса 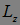 определяется азимутальной составляющей импульса
определяется азимутальной составляющей импульса 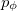
Выражения для других компонент  и
и  в сферических координатах довольно сложны, и мы выпишем здесь лишь оператор квадрата момента импульса
в сферических координатах довольно сложны, и мы выпишем здесь лишь оператор квадрата момента импульса
|
|
|
(5.3) |
Выражение (5.3) также достаточно сложно, и мы его практически использовать не будем. Но, даже только глядя на него, уже можно сделать важные выводы
|
Вместо формального математического доказательства последнего утверждения укажем источник этого свойства. Напомним, что  ,
,  и
и  являются операторами поворота системы вокруг осей x, y, z соответственно. Но результат двух таких поворотов зависит от их последовательности (рис. 5.3), поэтому и операторы не коммутируют между собой.
являются операторами поворота системы вокруг осей x, y, z соответственно. Но результат двух таких поворотов зависит от их последовательности (рис. 5.3), поэтому и операторы не коммутируют между собой.
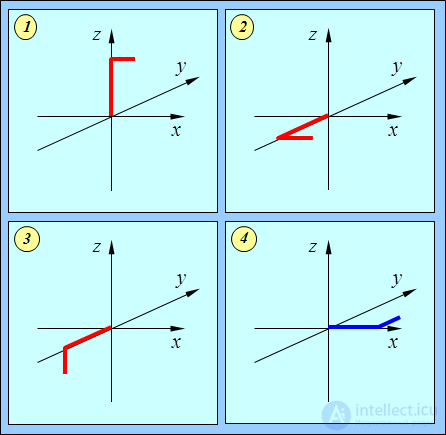
Рис. 5.3. Иллюстрация факта некоммутации операторов  ,
,  ,
,  ;
;
Г-образная фигура (1) сначала поворачивается на 90° вокруг оси х (2), затем — вокруг оси у (3).
При обратной последовательности тех же поворотов конечный результат получается другим (4)
Из сказанного вытекает важное следствие: одновременно измеримы лишь квадрат момента импульса и одна из его проекций (в качестве таковой обычно выбирают  ). Это значит, что вектор L в квантовой механике не имеет определенного направления и его нельзя считать классическим вектором с тремя определенными компонентами. Таким образом, «квантовый момент импульса» можно условно представить себе как вектор фиксированной длины (определенное значение квадрата момента импульса), направленный под фиксированным углом к оси z (определенное значение проекции), но прецессирующий вокруг этой оси (другие компоненты не определены). Это не более чем механическая аналогия (так называемая векторная модель), но она верно отражает существенные свойства момента импульса в квантовой механике.
). Это значит, что вектор L в квантовой механике не имеет определенного направления и его нельзя считать классическим вектором с тремя определенными компонентами. Таким образом, «квантовый момент импульса» можно условно представить себе как вектор фиксированной длины (определенное значение квадрата момента импульса), направленный под фиксированным углом к оси z (определенное значение проекции), но прецессирующий вокруг этой оси (другие компоненты не определены). Это не более чем механическая аналогия (так называемая векторная модель), но она верно отражает существенные свойства момента импульса в квантовой механике.
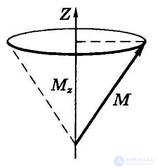
Рис. 5.4. Модель прецессирующего квантового момента импульса
Найдем теперь собственные функции и значения оператора  . Имеем уравнение
. Имеем уравнение

откуда

Заметим, что здесь  (без шляпки) — число, а не оператор.
(без шляпки) — число, а не оператор.
При повороте на угол  система возвращается в первоначальное состояние. Чтобы волновая функция
система возвращается в первоначальное состояние. Чтобы волновая функция  не изменилась, необходимо выполнение условия
не изменилась, необходимо выполнение условия

где m — целое (не обязательно положительное) число. Константа А определяется условием нормировки: интеграл от функции
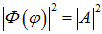
по углу  , изменяющемуся от 0 до
, изменяющемуся от 0 до  , должен быть равен единице
, должен быть равен единице

откуда следует, что

Таким образом, мы приходим к условию квантования проекции момента импульса:
|
Проекция момента импульса
|
Число m называют магнитным квантовым числом. Собственная волновая функция оператора  , соответствующая данному значению m, имеет вид
, соответствующая данному значению m, имеет вид
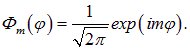
По сути дела, волновая функция  описывает плоскую волну, бегущую по окружности. Роль координаты играет угол
описывает плоскую волну, бегущую по окружности. Роль координаты играет угол  , роль волнового вектора — магнитное квантовое число m. Но значения переменной
, роль волнового вектора — магнитное квантовое число m. Но значения переменной  ограничены пределами 0 и
ограничены пределами 0 и  . Наша «круговая» волна как бы заключена в потенциальную яму и совершает финитное движение. Отсюда — квантование проекции момента импульса в соответствии с установленными выше законами квантовой механики.
. Наша «круговая» волна как бы заключена в потенциальную яму и совершает финитное движение. Отсюда — квантование проекции момента импульса в соответствии с установленными выше законами квантовой механики.
Найдем теперь правила квантования квадрата момента импульса. Решение соответствующего уравнения для собственных функций оператора  достаточно сложно, и мы заменим его не очень строгими, но простыми соображениями. Пусть в какой-то системе максимальная величина магнитного квантового числа т равна целому неотрицательному числу l. Тогда минимальное значение n, очевидно, равно –l, так что т пробегает 2l + 1 возможных значений:
достаточно сложно, и мы заменим его не очень строгими, но простыми соображениями. Пусть в какой-то системе максимальная величина магнитного квантового числа т равна целому неотрицательному числу l. Тогда минимальное значение n, очевидно, равно –l, так что т пробегает 2l + 1 возможных значений:

В классическом случае максимально возможная проекция момента импульса совпадает с модулем вектора  . Но не следует ожидать, что оператор
. Но не следует ожидать, что оператор  будет иметь собственные значения
будет иметь собственные значения  . Мы уже знаем, что даже при максимальной величине проекции момент импульса не параллелен оси z (иначе были бы известны все три компоненты момента). Стало быть, собственные значения оператора
. Мы уже знаем, что даже при максимальной величине проекции момент импульса не параллелен оси z (иначе были бы известны все три компоненты момента). Стало быть, собственные значения оператора  должны быть больше
должны быть больше  . Чему же они равны?
. Чему же они равны?
Если в пространстве нет выделенного направления, то любое значение n равновероятно, и среднее значение квадрата проекции момента на ось z равно

При выводе использовалась известная формула для суммы квадратов целых чисел.
Заметим, что все три координатные оси равноправны, следовательно, тот же результат справедлив для средних значений квадратов остальных операторов проекции момента импульса:
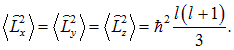
Но их сумма дает квадрат оператора момента импульса, среднее значение которого равно, таким образом,
|
|
|
(5.5) |
Именно этой формулой описываются собственные значения оператора квадрата момента импульса, так что условно можно считать, что длина вектора 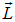 в квантовой механике равна
в квантовой механике равна
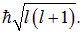
Целое неотрицательное квантовое число l называют азимутальным квантовым числом.
Для сравнения получим тем же способом классический ответ. Если l — максимальное значение  для классического вектора, то
для классического вектора, то  пробегает непрерывный ряд значений от –l до l с равной вероятностью dm/2l. Разница в том, что из-за непрерывности сумма заменяется интегралом, и мы получаем
пробегает непрерывный ряд значений от –l до l с равной вероятностью dm/2l. Разница в том, что из-за непрерывности сумма заменяется интегралом, и мы получаем

и аналогичные выражения для двух других средних. Складывая их, приходим к обычному результату классической физики

При больших значениях l оба результата совпадают (опять — принцип соответствия Бора).
Главный итог этого раздела — знакомство с правилами квантования момента импульса: собственное значение квадрата момента импульса определяется величиной азимутального квантового числа l, а проекция момента импульса — величиной магнитного квантового числа m, которое может принимать любое из значений

Если все-таки пытаться представить себе «квантовый вектор» момента количества движения как обычный вектор, то можно сказать, что при данной длине этого вектора он составляет с выделенной осью лишь строго определенные углы (рис. 5.5).
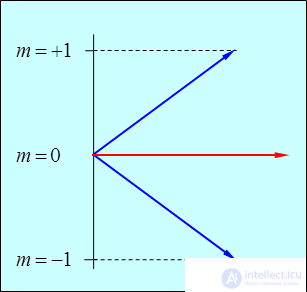
Рис. 5.5. Возможные ориентации вектора момента импульса при l = 1:
длина вектора равна 1.41, а его проекция на выделенную ось может принимать только значения 0 и +1 (в единицах 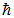 )
)
Подчеркнем еще раз, что эта картинка — всего лишь попытка изобразить квантовые свойства в классических образах.
Пример. Покажем, что согласно квантовой механике направление момента импульса  не может совпадать с выделенным в пространстве направлением и что в пределе больших азимутальных чисел
не может совпадать с выделенным в пространстве направлением и что в пределе больших азимутальных чисел  восстанавливаются классические свойства.
восстанавливаются классические свойства.
Поскольку модуль вектора момента импульса принимает значения
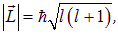
а его проекция на выделенное направление равна

то можно ввести угол  между направлением момента импульса и выделенной осью, так что
между направлением момента импульса и выделенной осью, так что  будет принимать лишь определенные значения
будет принимать лишь определенные значения

Отсюда следует, что минимальное значение угла  определяется максимальным значением его косинуса, достигаемым при m = l:
определяется максимальным значением его косинуса, достигаемым при m = l:

Видно, что при любом конечном значении l угол не равен нулю. Например, для состояний с l = 1 получаем

то есть  , а для состояний с l = 3 имеем
, а для состояний с l = 3 имеем
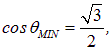
и  . Видно, что с ростом l минимальный угол между моментом импульса и осью уменьшается, и в пределе
. Видно, что с ростом l минимальный угол между моментом импульса и осью уменьшается, и в пределе

получаем  . Это и есть классическое свойство момента импульса: способность быть в точности параллельным любому выделенному направлению.
. Это и есть классическое свойство момента импульса: способность быть в точности параллельным любому выделенному направлению.
Стационарное уравнение Шредингера для водородоподобного атома (один электрон около ядра с зарядом Ze) имеет вид

Это уравнение удобно записать в сферических координатах:
|
|
|
(5.6) |
Разумеется, мы не станем решать это уравнение, но просто внимательно на него посмотрим.
Заметим, что та часть уравнения (5.6), которая зависит от углов, входит только в состав оператора квадрата момента импульса (5.3). Довольно ясен физический смысл этого члена. Представим себе, что в поле центральных сил по орбите радиусом r движется классическая частица с импульсом  . Ее момент количества движения равен
. Ее момент количества движения равен

где  — проекция импульса на направление, ортогональное радиусу-вектору
— проекция импульса на направление, ортогональное радиусу-вектору  . Обозначим
. Обозначим
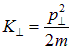
кинетическую энергию «ортогонального» движения. Ее можно выразить через квадрат момента количества движения:

Этот член добавляется к потенциальной энергии кулоновского притяжения к ядру, и его можно интерпретировать как потенциальную энергию в поле центробежных сил. Действительно, если  — потенциальная энергия, то ее производная по r должна дать соответствующие силы:
— потенциальная энергия, то ее производная по r должна дать соответствующие силы:

В конечном выражении легко узнать известную из классической механики формулу для центробежной силы. Квантовая механика, как это и должно быть, воспроизводит на новом уровне результаты классической: теперь момент импульса стал оператором, но вошел на прежних правах в выражение для оператора полной энергии (гамильтониана).
Любой оператор коммутирует сам с собой, и так как оператор квадрата момента (5.3) вообще не зависит от радиальной переменной r, то

коммутирует с гамильтонианом (5.6). Кроме того, оператор проекции момента импульса

коммутирует c

и, стало быть, с гамильтонианом. Следовательно, выполняются классические законы сохранения квадрата и одной проекции момента импульса. Эти законы сохранения справедливы для любого центрально-симметричного поля: специфика кулоновского взаимодействия пока нами не использовалась. Поэтому проекция и квадрат момента могут быть определены одновременно с энергией, и волновая функция стационарного состояния будет зависеть от квантовых чисел l и m. Однако в уравнении Шредингера (5.6) гамильтониан вовсе не зависит от оператора проекции момента импульса. Это значит, что энергия состояния не будет зависеть от магнитного квантового числа m. Иными словами, в любом центрально-симметричном поле имеется вырождение по n, кратность которого равна 21 + 1. Мы уже знаем, что источником вырождения должна служить та или иная симметрия. В классической физике движение частицы в центрально-симметричном поле всегда происходит по орбите, лежащей в одной плоскости. Но сама эта плоскость может быть произвольной в зависимости от начального положения и скорости частицы. Ясно, что значение полной энергии частицы не зависит при этом от ориентации плоскости орбиты в пространстве. Это и есть искомая симметрия, приводящая к вырождению по магнитному квантовому числу.
В кулоновском поле (равно как и в гравитационном) имеется еще одно специфическое вырождение, приводящее к тому, что энергия системы не зависит и от квантового числа l.
Вспомним опять классическую физику. В кулоновском поле финитное движение частицы совершается только по эллипсу. Возьмем в качестве аналогии искусственный спутник. Поместим его на каком-то расстоянии от Земли (то есть зададим потенциальную энергию) и придадим ему какую-то скорость (зададим кинетическую энергию). Таким образом, мы задали полную энергию спутника. Но определена ли его орбита? Разумеется, нет! При той же полной энергии направление скорости влияет на форму орбиты — от прямой линии (вертикальное падение) при нулевом моменте импульса до окружности максимально возможного радиуса при данной полной энергии. Нулевой момент соответствует чисто радиальным колебаниям сквозь центр притяжения, когда вовсе нет кругового движения, и эллипс вырождается в прямую линию (для спутника такое колебание невозможно, но микрочастицы — иное дело). Максимально возможный момент импульса достигается в обратном случае чисто круговой орбиты, когда совсем нет радиального движения. Важно, что его (максимального момента импульса) величина зависит от полной энергии спутника.
Подчеркнем, что ограничение сверху на возможную величину момента импульса 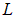 — при заданной полной механической энергии
— при заданной полной механической энергии  — имеет чисто классическое происхождение. Убедиться в этом можно следующим образом. Запишем классическое (не квантовое) выражение для
— имеет чисто классическое происхождение. Убедиться в этом можно следующим образом. Запишем классическое (не квантовое) выражение для  в виде
в виде
 .
.
Здесь  — кинетическая энергия радиального движения:
— кинетическая энергия радиального движения:  – радиальная составляющая скорости,
– радиальная составляющая скорости,  — эффективная потенциальная энергия, включающая в себя потенциальную энергию в поле центробежных сил. Ясно, что
— эффективная потенциальная энергия, включающая в себя потенциальную энергию в поле центробежных сил. Ясно, что  . Учитывая, что энергия связанных состояний меньше нуля, перепишем это неравенство в виде
. Учитывая, что энергия связанных состояний меньше нуля, перепишем это неравенство в виде

или
 .
.
Эффективная потенциальная энергия при отличном от нуля моменте импульса L имеет минимум в точке 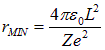 , ее минимальное значение равно
, ее минимальное значение равно
 .
.
Поскольку неравенство 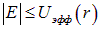 должно выполняться и в точке минимума, получаем
должно выполняться и в точке минимума, получаем
 или
или  .
.
Если в последнее неравенство подставить боровское выражение (3.3) для энергии водородоподобного иона и выражение (5.5) для квадрата момента, то получим неравенство
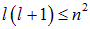 ,
,
которое имеет решение
 .
.
продолжение следует...
Часть 1 5. Теория атома
Часть 2 5.4. Спин электрона и тонкая структура спектров - 5. Теория
Часть 3 5.6. Принцип Паули и валентность элементов - 5. Теория атома
Часть 4 - 5. Теория атома
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика