5.4. Спин электрона и тонкая структура спектров - 5. Теория

Это продолжение увлекательной статьи про теория атома.

...

style="text-align:justify">Здесь n — боровский номер стационарной орбиты, или главное квантовое число (см. Об этом говорит сайт https://intellect.icu . ниже). Основанная на решении уравнения Шредингера (5.6) строгая квантовая теория дает тот же результат.

Итак, классическая физика подсказывает нам следующие свойства решений уравнения Шредингера:

Вооружившись знанием классической механики, мы можем смело приступать к изучению квантовой. Теперь станут понятны свойства решений уравнения Шредингера для атома водорода. Его решениями являются волновые функции, нумеруемые тремя квантовыми числами: . Про l и n уже много говорилось, а n — знакомое нам по атому Бора главное квантовое число, принимающее целые положительные значения. Разным наборам чисел отвечают разные волновые функции, общий вид которых — для любых возможных наборов чисел – нам сейчас не важен.

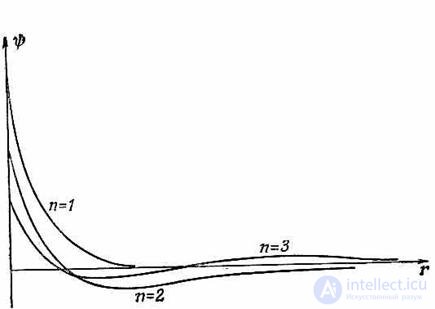
Рис. 5.6. Волновые функции трех первых состояний атома водорода с l = 0

Пример 1. Волновая функция основного состояния электрона в атоме водорода имеет вид

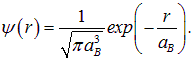
Найдем вероятности и 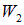обнаружить электрон внутри сфер с радиусам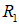и и .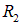

Вероятность обнаружить электрон в элементе объема dV равна

Так как волновая функция основного состояния не зависит от направления радиуса-вектора , а лишь от его модуля r, то можно написать выражение для вероятности обнаружить электрон в шаровом слое радиусом r и толщиной dr. Объем этого слоя равен 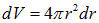(площадь поверхности, умноженная на толщину). Тогда

Теперь надо проинтегрировать вероятность no всем значениям r от 0 до R, получив вероятность W(R) найти электрон внутри сферы радиусом R:

Интеграл берется точно, и в результате получаем

откуда находим

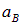Здесь e — основание натурального логарифма. Разность дает вероятность найти электрон между сферами с радиусами и . Видно, что численно эта вероятность близка к вероятности . Зато вероятность обнаружить электрон за пределами сферы радиусом заметно меньше: она равна, как нетрудно догадаться,

Иными словами, с вероятностью более 76% электрон в основном состоянии пребывает на расстоянии не более двух радиусов Бора от ядра.

Пример 2. Найдем электростатический потенциал, создаваемый атомом водорода в основном состоянии.

Возьмем любую точку на расстоянии R от ядра. Электростатический потенциал в ней создается, во-первых, положительным зарядом е ядра и, во-вторых, той частью заряда электрона, которая находится внутри сферы радиусом R. Хорошо известно, что сферически симметричное распределение заряда не создает поля во внутренних областях. Поэтому часть электронного облачка, находящаяся дальше выбранной точки, не внесет вклада в потенциал. Поскольку в уравнении (5.7) вычислена вероятность W(R) нахождения электрона внутри сферы радиусом R, то отрицательный заряд внутри этой сферы равен –eW(R). Поэтому потенциал в точке R, создаваемый эффективным зарядом

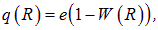
имеет вид

На больших расстояниях потенциал (5.8) убывает экспоненциально, то есть гораздо быстрее обычного кулоновского потенциала точечного заряда. Это — так называемый эффект экранировки: отрицательный заряд электрона компенсирует положительный заряд ядра. При

потенциал (5.8) переходит в обычный кулоновский потенциал: мы проникли внутрь электронного облачка, где оно уже не экранирует заряд ядра.

Для энергии из уравнения Шредингера получается в точности такая же формула, что и из теории Бора:

Как видно, энергия действительно не зависит от квантовых чисел l, m. При этом, как следует из свойств решений уравнения (5.6), азимутальное квантовое число l принимает целые значения от 0 до n – 1. И это свойство, угаданное нами на основе классической физики, воспроизвелось в квантовой механике.

Удивительно, как квантовая механика, низвергнувшая столько классических представлений, дает аналогичные результаты там, где в дело вступают свойства симметрии системы. Отсюда вывод: симметрия играет более важную роль, чем конкретные физические законы. Когда-нибудь будут открыты новые законы, которые обобщат и квантовую механику, и все теории, которые ныне находятся на переднем крае науки. Но свойства симметрии системы так или иначе проявят себя.

Отличие квантовой механики от теории Бора — более богатая структура состояний: состояние определяется тремя квантовыми числами, как и в трехмерном потенциальном ящике. Кстати, это не случайно. Три квантовых числа в потенциальной яме и в атоме водорода — отражение трехмерности нашего пространства. Подсчитаем кратность вырождения, то есть число различных состояний с одной и той же энергией (главным квантовым числом n). При данном значении n число l пробегает все целые числа от 0 до n – 1, и каждому из них соответствует 2l + 1 значение n. Поэтому кратность вырождения N определяется соотношением

При n = 1 имеем N = 1, то есть основной уровень не вырожден. При n=2 кратность вырождения равна 4: один уровень с l = 0 и три уровня с l = 1 и различными проекциями момента импульса n = –1, 0, +1. При n = 3 кратность вырождения N = 9: один уровень с l = 0, три уровня с l = 1 и пять уровней (по числу проекций) с l = 2. Для классификации состояний энергии по значению квантового числа l применяют условные обозначения, позаимствованные из спектроскопии, где они появились еще до создания теории атома:

Главное квантовое число ставится впереди символа. Примеры возможных состояний:

1s, 2s, 2p, 3s, 3p, 3d, 4s, 4р, 4d, 4f и т. д.

Рис. 5.7. Собственные функции гамильтониана для атома водорода. Показаны поперечные сечения плотности вероятностей, величина которой отражена цветом (черный цвет соответствует минимальной плотности вероятности, а белый ̶ максимальной). Каждому столбцу отвечает определенное значение квантового числа l. Главное квантовое число n отмечено справа от каждого ряда. Для всех картин квантовое число m = 0. Проекция момента импульса берется на вертикальную ось z. Сечение взято в плоскости x, z. Плотность вероятности в трехмерном пространстве получается при вращении картинки вокруг оси z

Во избежание недоразумений отметим, что указанный здесь порядок следования состояний — исключительно «алфавитный». Если расположить состояния в порядке возрастания их энергий, то в многоэлектронных атомах список будет выглядеть иначе, например, начиная с калия (Z = 19), состояния 3d и 4s поменяются местами. Причины таких «инверсий» обсуждаются в соответствующих разделах далее.

При переходе электрона с более высокого уровня энергии на более низкий излучается фотон, уносящий собственный угловой момент, равный ħ (авторы просят принять это на веру). Следовательно, разрешены только переходы с изменением l на единицу: возникает правило отбора

Это значит, что в атоме водорода допустимы переходы

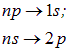
и т. д., приводящие к тем же спектральным сериям, что и теория Бора. Более богатая структура состояний не проявляется пока в большем разнообразии атомных уровней и, соответственно, спектров из-за вырождения.

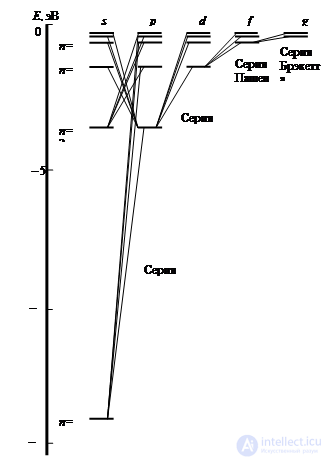
Рис. 5.8. Схема уровней энергии и возможных переходов между уровнями в атоме водорода

Говоря о вырождении уровней, мы имели в виду водородоподобный атом. В более сложных атомах или в присутствии внешних электромагнитных полей вырождение, как говорят, снимается и появляется зависимость энергии от чисел 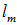. Любая не кулоновская центрально-симметричная поправка к потенциальной энергии приведет к зависимости уровней энергии от l (наблюдается, например, в щелочных металлах). В классической физике такая поправка к обычному закону притяжения (например, планеты к Солнцу) превращает эллиптические орбиты в незамкнутые кривые. Обращаясь по таким орбитам, планета как бы движется по обычному эллипсу, который дополнительно вращается как целое, прецессирует в той же плоскости. Подобный эффект — вращение перигелия Меркурия — предсказала общая теория относительности. Новое движение приводит к дополнительной энергии вращения, зависящей от l. В результате энергия уровня 2s перестанет совпадать с энергией уровня 2p_p и т. д.

Любое не центрально-симметричное поле (например, магнитное) снимет вырождение по m_m. В классической физике магнитное поле вызывает прецессию плоскости вращения вокруг направления поля и также появление из-за этого вращения дополнительной энергии. Сказанное можно сформулировать в виде общего вывода:

Всякое дополнительное взаимодействие, нарушающее симметрию системы, снимает соответствующее ей вырождение уровней энергии. На эксперименте снятие вырождения проявляет себя в расщеплении прежних спектральных линий на несколько компонент.

5.4. Спин электрона и тонкая структура спектров

Дальнейшее исследование атомных спектров показало, что многие спектральные линии имеют два близких компонента. Так, еще в 1887 г. А. Майкельсон обнаружил расщепление 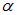— линии серии Бальмера в водороде, порождаемой переходом

Она оказалась состоящей из двух линий со средней длиной волны 6 563 Å.

Рис. 5.9. Альберт Абрахам Майкельсон 1852–1931

Разность длин волн равна 0.14 Å (то есть относительная величина расщепления порядка 10^–5 ). Были обнаружены и линии, расщепленные на 3, 4 и более компонентов. Расщепление линий, как мы теперь понимаем, означает расщепление энергетических уровней атома: у них появляется, как говорят, тонкая структура. Значит, существует неучтенное взаимодействие. Мы говорили, что расщепление линий возникает, например, когда наложенное внешнее поле нарушает симметрию системы. А здесь неучтенное взаимодействие проявляется в отсутствие внешних полей, то есть оно должно быть связано с какими-то внутренними свойствами атома.

Оказалось, что это действительно проявление внутренних свойств, но не атома в целом, а электрона. В 1925 г. С. Гаудсмит и Дж. Уленбек выдвинули гипотезу спина электрона: они предположили существование у электрона собственного момента импульса, не связанного с орбитальным движением. Сначала спин представляли себе как верчение (англ. spin) электрона вокруг собственной оси (аналог суточного вращения Земли). Потом осознали, что «верчение» нельзя понимать буквально: численные оценки давали линейную скорость верчения, превышающую скорость света в вакууме.

Рис. 5.10. Сэмюэл Абрахам Гаудсмит 1902–1978

Рис. 5.11. Джо́рдж Ю́джин Уленбе́к 1900–1988

Его существование остается загадкой, если находиться только в рамках квантовой механики Гейзенберга — Шредингера. Естественное объяснение спин получил только в релятивистской квантовой теории П. Дирака, соединившей теорию относительности с квантовой механикой.

Рис. 5.12. Поль Адриен Морис Дира́к, 1902–1984

Из опытов следовало, что электрону надо приписать спиновое квантовое число s = 1/2, имеющее те же свойства (см. формулу (5.5)), что и квантовое число l. Принято для краткости спиновое квантовое число называть спином. В дальнейшем мы тоже будем использовать эту, общепринятую терминологию.

Соответственно, существует единственное собственное значение оператора квадрата спина

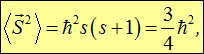
а проекция спина на какую-то ось (пробегая через единицу ħ все значения от максимального до минимального) записывается в виде

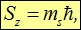
где 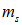принимает лишь два значения

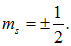
Число называют магнитным спиновым квантовым числом.

Откуда же взялось расщепление спектральных линий? Попытаемся понять это с помощью полуклассических рассуждений. В классической физике любое вращение электрического заряда создает магнитное поле. Вращающийся по орбите радиусом R классический электрон можно представить как виток с током силой l, охватывающий площадь 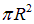, то есть как магнитный диполь с магнитным моментом

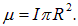
(Эту формулу знал еще Ш. Кулон).

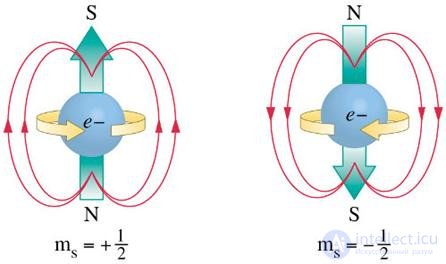
Рис. 5.13. Модель спина и магнитного момента электрона в рамках классической физики

Классическая оценка: электрон на орбите радиусом R и скоростью v имеет период обращения

Возьмем какую-нибудь точку на орбите. За время T через нее проходит заряд е, то есть сила тока по определению равна

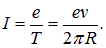
Кроме того, электрон имеет орбитальный момент

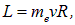
так что ток можно выразить через орбитальный момент, исключив скорость электрона:

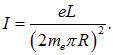
Тогда орбитальный магнитный момент, создаваемый электроном, равен

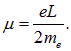
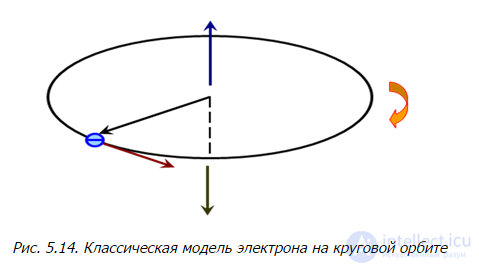
Рис. 5.14. Классическая модель электрона на круговой орбите

Заменим теперь в соответствии с правилами квантования

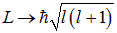
и получим выражение для орбитального магнитного момента, которое может быть выведено и более строго:

Отсюда следуют выводы:

Эксперименты показали, что спин электрона обладает двойным магнетизмом: собственный магнитный момент электрона, связанный со спином, равен

то есть гиромагнитное отношение для него оказалось в два раза большим 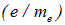. Это — лишнее доказательство того, что электрон нельзя представлять себе как заряженный шарик, вращающийся вокруг собственной оси: в таком случае должно было бы получиться обычное гиромагнитное отношение. Для проекции собственного магнитного момента имеем

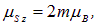
и поскольку

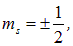
то

В итоге для проекции спинового магнитного момента снова получились целые кратные магнетона Бора, как и для орбитального движения. По какой-то причине природа предпочитает иметь дело с целым магнетоном Бора, а не с его частями. Поэтому полуцелое значение собственного момента количества движения она компенсирует двойным гиромагнитным отношением.

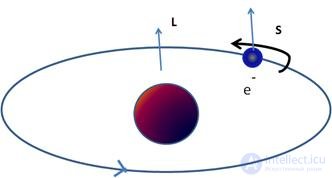
Рис. 5.15. Иллюстрация орбитального и спинового моментов электрона

Теперь можно понять, почему наличие у электрона собственного магнитного момента приводит к появлению какого-то неучтенного до сих пор взаимодействия. Для этого опять перейдем на полуклассический язык. Орбитальное движение электрона создает магнитное поле, которое действует на собственный магнитный момент электрона. Подобным образом магнитное поле Земли воздействует на стрелку компаса. Энергия этого взаимодействия сдвигает энергетические уровни атома, причем величина сдвига зависит, вообще говоря, от спинового и орбитального моментов количества движения.

Важный вывод:

Пример 1. Оценим расщепление уровней энергии вследствие взаимодействия спинового и орбитального магнитного моментов электрона в атоме водорода.

Круговой виток радиусом R с током силой I порождает в центре магнитное поле

В этой главе было показано, что вращающийся по орбите электрон можно представить как виток с током

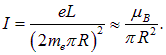
Здесь для оценки мы положили

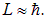
Тогда получаем для магнитного поля, создаваемого орбитальным движением электрона в атоме, величину порядка

Энергия взаимодействия собственного магнитного момента электрона с этим магнитным полем равна по порядку величины

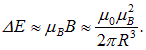
Для оценки положим R равным боровскому радиусу первой орбиты 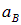. Подставляя сюда выражения для 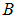и 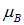и учитывая, что

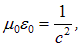
получаем оценку сдвига энергетических уровней

где — введенная выше (см. (3.3)) постоянная тонкой структуры. Энергия первого уровня атома водорода, как известно, равна

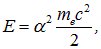
так что (3.13) можно переписать как

Поскольку

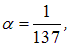
a E = 13 6эВ, то

а относительный сдвиг уровней

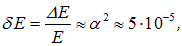
что соответствует экспериментальным данным.

Это и есть оценка (не расчет) искомого расщепления уровней. В сущности, расщепление уровней — это релятивистский эффект: по Бору скорость электрона на первой орбите

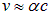
и

Поэтому не удивительно, что до конца свойства спина могут быть поняты только в релятивистской квантовой теории. Мы не ставим себе такую задачу, но просто будем учитывать наличие у электрона этого удивительного свойства.

Экспериментальное доказательство существования спина электрона было дано в опыте Штерна — Герлаха в 1922 г. Идея опыта состоит в том, что в магнитном поле, неоднородном по оси z, на электроны действует смещающая сила, направленная вдоль поля. Происхождение этой силы проще уяснить сначала на примере электрического диполя, помещенного в электрическое поле. Электрический диполь представляет собой пару противоположных зарядов , расположенных на малом расстоянии l друг от друга. Величина электрического дипольного момента определяется как

причем вектор l считается направленным от отрицательного заряда к положительному.

Пусть положительный заряд находится в точке r, а отрицательный — в точке , так что

Пусть диполь помещен в электрическое поле с напряженностью .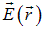

продолжение следует...

Продолжение:

Часть 1 5. Теория атома
Часть 2 5.4. Спин электрона и тонкая структура спектров - 5. Теория
Часть 3 5.6. Принцип Паули и валентность элементов - 5. Теория атома
Часть 4 - 5. Теория атома