Введение в общую топологию, разделы топологии

Привет, Вы узнаете о том , что такое топология, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое топология , настоятельно рекомендую прочитать все из категории Общая топология.

Тополо́гия (от др.-греч. τόπος — место и λόγος — слово, учение) — раздел математики, изучающий:

• в самом общем виде — явление непрерывности;
• в частности — свойства пространств, которые остаются неизменными при непрерывных деформациях. Например, связность, ориентируемость, компактность.

В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов (например, расстояние между парой точек). Например, с точки зрения топологии кружка с ручкой и бублик (полноторий) неразличимы. При этом часто топология применяется к объектам, далеким от геометрических.

Весьма важными для топологии являются понятия гомеоморфизма и гомотопии (упрощенно: это типы деформации, происходящие без разрывов и склеиваний).

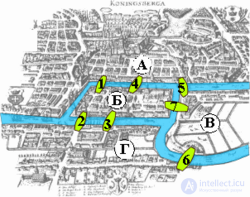
Семь мостов Кенигсберга — известная задача, решенная Эйлером и способствовавшая развитию топологии

Раздел математики, ныне называемый топологией, берет свое начало с изучения некоторых задач геометрии.

Различные источники указывают на первые топологические по духу результаты в работах Лейбница и Эйлера, однако термин «топология» впервые появился в 1847 году в работе Листинга. Листинг определяет топологию так:

«Под топологией будем понимать учение о модальных отношениях пространственных образов — или о законах связности, взаимного положения и следования точек, линий, поверхностей, тел и их частей или их совокупности в пространстве, независимо от отношений мер и величин».

Когда топология еще только зарождалась (XVIII—XIX века), ее называли геометрией размещения (лат. geometria situs) или анализом размещения (лат. analysis situs). Приблизительно с 1925 по 1975 годы топология являлась одной из самых бурно развивающихся отраслей математики.

Общая топология зародилась в конце XIX века — и оформилась в самостоятельную математическую дисциплину в начале XX века. Основополагающие работы принадлежат: Хаусдорфу, Пуанкаре (цикл статей Analysis situs), Александрову, Урысону, Брауэру.

Общая топология, или теоретико-множественная топология, — раздел топологии о непрерывности в чистом виде. Здесь исследуются фундаментальные вопросы топологии, а также отдельные вопросы, такие как связность и компактность.

О́бщая тополо́гия (теоре́тико-мно́жественная тополо́гия) — раздел топологии, в котором изучаются понятия непрерывности и предела в наиболее общем смысле.

Традиционный подход к общей топологии — теоретико-множественный. Множество называется топологическим пространством, когда задано определенное семейство его открытых подмножеств, удовлетворяющее аксиомам. Возможно много способов задания структуры топологического пространства на одном множестве: от дискретной до нехаусдорфовой антидискретной (тривиальной) топологии, склеивающей все точки вместе.

Базовые понятия теории множеств, такие как множество, функция, ординальные числа, кардинальные числа, аксиома выбора, лемма Цорна, не являются предметом общей топологии, но активно ею используются. Общая топология включает следующие разделы: свойства топологических пространств и их отображений, операции над топологическими пространствами и их отображениями, классификация топологических пространств. Самостоятельное направление общей топологии — теория размерности.

В отличие от дифференциальной и алгебраической топологии, общая топология сосредоточена на изучении наиболее общего вида непрерывных отображений топологических пространств друг в друга, а не в пространства, наделенные более сложными структурами, прежде всего — алгебраическими.

Глоссарий общей топологии включает такие понятия как окрестности, замыкания множеств (а также внутренности), компактность множеств, сходимость последовательностей и фильтров. Понятие предела функции, вводимое в общей топологии, допускает дальнейшее обобщение в рамках теории псевдотопологических пространств.

Общая топология зародилась в конце XIX века и оформилась в самостоятельную математическую науку в начале XX веке. Основополагающие работы принадлежат Феликсу Хаусдорфу, Анри Пуанкаре, Павлу Александрову, Павлу Урысону, Лейтзену Брауэру. В частности, была решена одна из главных задач общей топологии — нахождение необходимых и достаточных условий метризуемости топологического пространства.

Наиболее бурное развитие общей топологии как самостоятельной ветви знания происходило в середине XX века, к началу XXI века она скорее является вспомогательной дисциплиной, «обслуживающей» многие области математики: алгебраическую топологию, функциональный анализ, комплексный анализ, теорию графов.

Алгебраическая топология — раздел топологии о непрерывности с использованием алгебраических объектов, вроде гомотопических групп и гомологий.

Алгебраическая тополо́гия (устаревшее название: комбинаторная топология) — раздел топологии, изучающий топологические пространства путем сопоставления им алгебраических объектов (групп, колец и т. д.), а также поведение этих объектов под действием различных топологических операций.

Методы алгебраической топологии основаны на предположении, что общеалгебраические структуры устроены проще, чем топологические.

Важным инструментом алгебраической топологии являются так называемые группы гомологий (например, симплициальные или сингулярные). Каждому топологическому пространству соответствует в каждой размерности n своя абелева группа гомологий , а каждому непрерывному отображению соответствует гомоморфизм групп , причем композиции отображений соответствует композиция гомоморфизмов , а тождественному отображению соответствует тождественный гомоморфизм id∗. На языке теории категорий это означает, что n -я группа гомологий является ковариантным функтором из категории топологических пространств в категорию абелевых групп.

Помимо различных теорий гомологий (сейчас очень большое значение приобрели экстраординарные гомологии, например, теория бордизмов или K -теория), для алгебраической топологии важны гомотопические группы . Из них главной является — так называемая фундаментальная группа, которая, в отличие от групп всех других размерностей, может быть неабелевой.

Дифференциальная топология — раздел топологии о гладких многообразиях с точностью до диффеоморфизма и их включениях (размещениях) в других многообразиях.

Этот раздел включает в себя маломерную топологию, в том числе теорию узлов и четырехмерную топологию.

Дифференциа́льная геоме́трия — раздел математики, изучающий гладкие многообразия, обычно с дополнительными структурами. Они находят множество применений в физике, особенно в общей теории относительности.

Основные подразделы дифференциальной геометрии:

Часто дифференциальная геометрия рассматривается как неделимый раздел вместе с дифференциальной топологией. Различиями между этими разделами могут быть наличие или отсутствие дополнительных структур на гладком многообразии, но может быть также наличие или отсутствие локальных инвариантов: в дифференциальной топологии рассматриваются такие структуры на многообразиях, что у любой пары точек можно найти одинаковые окрестности, тогда как в дифференциальной геометрии, вообще говоря, могут присутствовать локальные инварианты (такие как кривизна), которые могут различаться в точках. Например, симплектическая структура таких инвариантов не имеет, и, наряду с симплектической геометрией, рассматривается «симплектическая топология».

Математическая предметная классификация выделяет для дифференциальной геометрии раздел верхнего уровня 53, а дифференциальную топологию относит в качестве блока второго уровня 57Rxx в разделе «Многообразия и клеточные комплексы».

Дифференциальная геометрия возникла и развивалась в тесной связи с математическим анализом, который сам в значительной степени вырос из задач геометрии. Многие геометрические понятия предшествовали соответствующим понятиям анализа. Так, например, понятие касательной предшествовало понятию производной, понятие площади и объема — понятию интеграла.

Возникновение дифференциальной геометрии относится к XVIII веку и связано с именами Эйлера и Монжа. Первое сводное сочинение по теории поверхностей написано Монжем («Приложение анализа к геометрии», 1795). В 1827 году Гаусс опубликовал работу «Общее исследование о кривых поверхностях», в которой заложил основы теории поверхностей в ее современном виде. С тех пор дифференциальная геометрия перестала быть только приложением анализа и заняла самостоятельное место в математике.

Огромную роль в развитии всей геометрии, в том числе и дифференциальной геометрии, сыграло открытие неевклидовой геометрии. Риман в своей лекции «О гипотезах, лежащих в основаниях геометрии» (1854) заложил основы римановой геометрии, наиболее развитой части современной дифференциальной геометрии.

Теоретико-групповая точка зрения Клейна, изложенная в его «Эрлангенской программе» (1872), то есть: геометрия — учение об инвариантах групп преобразований, в применении к дифференциальной геометрии была развита Картаном, который построил теорию пространств проективной связности и аффинной связности.

Дифференциальная топология является гораздо более молодым разделом математики: он начал развиваться только в начале XX века.

Вычислительная топология — раздел, находящийся на пересечении топологии, вычислительной геометрии и теории вычислительной сложности. Занимается созданием эффективных алгоритмов для решения топологических проблем и применением топологических методов для решения алгоритмических проблем, возникающих в других областях науки.

Алгоритмическая топология , или вычислительная топология , является подразделом топологии , пересекающимся с областями компьютерной науки , в частности, с вычислительной геометрией и теорией сложности вычислений .

Основная задача алгоритмической топологии, как следует из ее названия, заключается в разработке эффективных алгоритмов для решения задач, которые естественным образом возникают в таких областях, как вычислительная геометрия , графика , робототехника , социальные науки , структурная биология и химия , с использованием методов вычислительной топологии .

Большое семейство алгоритмов, касающихся 3-многообразий, вращается вокруг теории нормальных поверхностей , которая представляет собой термин, охватывающий несколько методов преобразования задач теории 3-многообразий в задачи целочисленного линейного программирования.

• Алгоритм распознавания 3-сфер Рубинштейна и Томпсона . Об этом говорит сайт https://intellect.icu . Это алгоритм, который принимает в качестве входных данных триангулированное 3-многообразие и определяет, гомеоморфно ли многообразие 3 -сфере . Он имеет экспоненциальное время выполнения по числу тетраэдральных симплексов в исходном 3-многообразии, а также экспоненциальный профиль памяти. Сол Шлеймер продолжил, показав, что проблема лежит в классе сложности NP . Кроме того, Рафаэль Центнер показал, что проблема лежит в классе сложности coNP, при условии, что верна обобщенная гипотеза Римана. Он использует инстантонную калибровочную теорию, теорему о геометризации 3-многообразий и последующую работу Грега Куперберга по сложности обнаружения заузленности.
• Разложение 3-многообразий методом связной суммы также реализовано в Regina , имеет экспоненциальное время выполнения и основано на алгоритме, похожем на алгоритм распознавания 3-сфер.
• Определение того, что 3-многообразие Зейферта-Вебера не содержит несжимаемой поверхности, было алгоритмически реализовано Бертоном, Рубинштейном и Тиллманном и основано на теории нормальных поверхностей.
• Алгоритм Мэннинга — это алгоритм для поиска гиперболических структур на 3-многообразиях, фундаментальная группа которых имеет решение проблемы тождества слов .

В настоящее время разложение JSJ не реализовано алгоритмически в компьютерном программном обеспечении. Также не реализовано разложение по сжатым телам. Существуют некоторые очень популярные и успешные эвристики, такие как SnapPea , которая успешно вычисляет приближенные гиперболические структуры на триангулированных 3-многообразиях. Известно, что полная классификация 3-многообразий может быть выполнена алгоритмически. Фактически, известно, что решение вопроса об эквивалентности (гомеоморфности) двух замкнутых ориентированных 3-многообразий, заданных триангуляцией (симплициальными комплексами), является элементарно рекурсивным . Это обобщает результат о распознавании 3-сфер.

• SnapPea реализует алгоритм преобразования плоской диаграммы узла или зацепления в триангуляцию с остриями. Время выполнения этого алгоритма практически линейно зависит от количества пересечений на диаграмме, а потребление памяти невелико. Этот алгоритм аналогичен алгоритму Виртингера для построения представлений фундаментальной группы дополнительных зацеплений, заданных плоскими диаграммами. Аналогичным образом, SnapPea может преобразовывать хирургические представления 3-многообразий в триангуляции заданного 3-многообразия.
• Д. Терстон и Ф. Костантино разработали процедуру построения триангулированного 4-многообразия из триангулированного 3-многообразия. Аналогичным образом, ее можно использовать для построения хирургических представлений триангулированных 3-многообразий, хотя эта процедура явно не описана в виде алгоритма, в принципе, ее время выполнения должно быть полиномиальным относительно числа тетраэдров заданной триангуляции 3-многообразия.
• У С. Шлеймера есть алгоритм, который создает триангулированное 3-многообразие, используя на входе слово (в генераторах твиста Дена ) для группы классов отображений поверхности. Это 3-многообразие использует это слово в качестве прикрепляющего отображения для разбиения Хегора 3-многообразия. Алгоритм основан на концепции слоистой триангуляции .

Известно, что определение того, является ли узел тривиальным, относится к классам сложности NP , а также к co-NP . Задача определения рода узла в 3-многообразии является NP-полной ; однако, хотя NP остается верхней границей сложности определения рода узла в R 3 или S 3 , по состоянию на 2006 год было неизвестно, является ли алгоритмическая задача определения рода узла в этих конкретных 3-многообразиях все еще NP-трудной .

• Методы вычисления гомотопических групп сфер .
• Вычислительные методы решения систем полиномиальных уравнений .
• У Брауна есть алгоритм для вычисления гомотопических групп пространств, являющихся конечными комплексами Постникова , хотя он не считается широко реализуемым.

Вычисление групп гомологии клеточных комплексов сводится к приведению граничных матриц к нормальной форме Смита . Хотя алгоритмически эта задача полностью решена, существуют различные технические препятствия для эффективных вычислений для больших комплексов. Существует два основных препятствия. Во-первых, базовый алгоритм в форме Смита имеет кубическую сложность по размеру задействованной матрицы, поскольку использует операции над строками и столбцами, что делает его непригодным для больших клеточных комплексов. Во-вторых, промежуточные матрицы, получаемые в результате применения алгоритма в форме Смита, заполняются, даже если он начинается и заканчивается разреженными матрицами.

• Эффективные и вероятностные алгоритмы нормальной формы Смита, найденные в библиотеке LinBox .
• Простые гомотопические редукции для предварительной обработки гомологических вычислений, как в программном пакете Perseus .
• Алгоритмы для вычисления постоянной гомологии отфильтрованных комплексов, как в пакете TDAstats R.
• В некоторых приложениях, например, в TDA, полезно иметь представителей классов (ко)гомологий, которые были бы как можно «малее». Это известно как проблема локализации (ко)гомологий. На триангулированных многообразиях, если задана цепь, представляющая класс гомологии, в общем случае аппроксимация гомологичной цепи с минимальным носителем является NP-трудной задачей. Однако частный случай аппроксимации локализации 1-когомологий на триангулированных 2-многообразиях является одной из трех известных задач, сложность которых эквивалентна гипотезе об уникальных играх .

Маломерная топология

Маломерная топология — направление в топологии, изучающее многообразия или, в более общем смысле, топологические пространства четырех или менее размерностей. В частности, к направлению относятся структурная теория 3-многообразий и 4-многообразий, теория узлов и теория кос. Направление можно рассматривать как часть геометрической топологии. (Изучение одномерных топологических пространств также иногда относится к маломерной топологии, хотя чаще рассматривается как часть теории континуума.)

Ряд результатов 1960-х годов подчеркнули особую значимость малых размерностей в топологии. Например, доказательство гипотезы Пуанкаре в пяти или более размерностях (Смейл, 1961) сделало размерности три и четыре самыми трудными; и, действительно, они потребовали новых методов, в то время как свобода более высоких размерностей означала, что вопросы можно было свести к вычислительным методам, доступным в теории хирургии. Гипотеза Терстона, в конце 1970-х годов, предложила основу, которая предполагала, что геометрия и топология тесно переплетаются в малых размерностях, а доказательство Терстона геометризации многообразий Хакена использовало различные инструменты из ранее лишь слабо связанных областей математики. Открытие Воаном Джонсом многочлена Джонса в начале 1980-х годов не только привело теорию узлов в новое русло, но и породило до сих пор загадочные связи между маломерной топологией и математической физикой. В 2002 году Григорий Перельман объявил о доказательстве трехмерной гипотезы Пуанкаре, используя поток Риччи Ричарда Гамильтона — идею, принадлежащую области геометрического анализа.

Существует несколько теорем, которые фактически утверждают, что многие из основных инструментов, используемых для изучения многомерных многообразий, неприменимы к маломерным многообразиям.

Теорема Стинрода утверждает, что ориентируемое трехмерное многообразие имеет тривиальное касательное расслоение. Другими словами, единственный характерный класс 3-многообразия — это препятствие к ориентируемости.

Любое замкнутое 3-многообразие является границей 4-многообразия, результат следует из теоремы Дена — Ликориша через расщепление Хегора 3-многообразия, а также следует из вычислений Рене Тома для кольца кобордизмов замкнутых многообразий.

Цифровая топология

Цифровая топология имеет дело со свойствами и особенностями двумерных (2D) или трехмерных (3D) цифровых изображений , которые соответствуют топологическим свойствам (например, связность ) или топологическим особенностям (например, границы ) объектов.

Концепции и результаты цифровой топологии используются для определения и обоснования важных (низкоуровневых) алгоритмов анализа изображений , включая алгоритмы прореживания , трассировки границ или поверхностей, подсчета компонентов или туннелей или заполнения областей.

Цифровая топология была впервые изучена в конце 1960-х годов исследователем в области компьютерного анализа изображений Азриэлем Розенфельдом (1931–2004), чьи публикации по этой теме сыграли важную роль в становлении и развитии этой области. Сам термин «цифровая топология» был придуман Розенфельдом, который впервые использовал его в публикации 1973 года.

Смежная работа, называемая топологией ячеек сетки , которую можно рассматривать как ссылку на классическую комбинаторную топологию , появилась в книге Павла Александрова и Хайнца Хопфа , Топология I (1935). Розенфельд и др. предложили цифровую связность, такую ​​как 4-связность и 8-связность в двух измерениях, а также 6-связность и 26-связность в трех измерениях. Метод маркировки для вывода компонента связности изучался в 1970-х годах. Теодосиос Павлидис (1982) предложил использовать графовые алгоритмы, такие как метод поиска в глубину для нахождения компонентов связности. Владимир А. Ковалевский (1989) расширил топологию ячеек сетки Александрова-Хопфа 2D на три и более измерений. Он также предложил (2008) более общую аксиоматическую теорию локально конечных топологических пространств и абстрактных комплексов клеток, ранее предложенную Эрнстом Штайницем (1908). Это топология Александрова . Книга 2008 года содержит новые определения топологических шаров и сфер, не зависящие от метрики, а также многочисленные приложения к цифровому анализу изображений.

В начале 1980-х годов изучались цифровые поверхности . Дэвид Моргенталер и Розенфельд (1981) дали математическое определение поверхностей в трехмерном цифровом пространстве. Это определение включает в общей сложности девять типов цифровых поверхностей. Цифровое многообразие было изучено в 1990-х годах. Рекурсивное определение цифрового k-многообразия было интуитивно предложено Ченом и Чжаном в 1993 году. Многочисленные приложения были найдены в обработке изображений и компьютерном зрении.

Базовый (ранний) результат в области цифровой топологии гласит, что двумерные бинарные изображения требуют альтернативного использования 4- или 8-элементной смежности или « пиксельной связности » (для пикселей «объекта» или «не объекта» ) для обеспечения базовой топологической двойственности разделения и связности. Это альтернативное использование соответствует открытым или закрытым множествам в топологии ячеек двумерной сетки , и результат обобщается на трехмерный мир: альтернативное использование 6- или 26-элементной смежности соответствует открытым или закрытым множествам в топологии ячеек трехмерной сетки . Топология ячеек сетки также применима к многоуровневым (например, цветным) двумерным или трехмерным изображениям, например, на основе общего порядка возможных значений изображения и применения «правила максимальной метки» (см. книгу Клетта и Розенфельда, 2004).

Цифровая топология тесно связана с комбинаторной топологией . Основные различия между ними заключаются в следующем: (1) цифровая топология изучает в основном цифровые объекты, образованные ячейками сетки (ячейками целочисленных решеток), а не более общими комплексами ячеек , и (2) цифровая топология также имеет дело с нежордановыми многообразиями.

Комбинаторное многообразие — это разновидность многообразия, являющаяся дискретизацией многообразия. Обычно под ним понимается кусочно-линейное многообразие , образованное симплициальными комплексами . Цифровое многообразие — это особый вид комбинаторного многообразия, определяемого в цифровом пространстве, то есть в пространстве ячеек сетки.

Цифровая форма теоремы Гаусса–Бонне такова: пусть M — замкнутое цифровое двумерное многообразие в прямой смежности (т.е. (6,26)-поверхность в трехмерном пространстве). Формула для рода:

,

гдеобозначает множество точек поверхности, каждая из которых имеет i смежных точек (Чэнь и Жун, ICPR 2008). Если M односвязно, то есть, затем. (Вау!! 😲 Ты еще не читал? Это зря! Эйлерова характеристика .)

• Топологическое пространство
• Глоссарий общей топологии
• Вычислительная топология (изучение топологической природы вычислений)
• Вычислительная геометрия
• Топологический анализ данных
• Пространственно-временное мышление
• Экспериментальная математика
• Геометрическое моделирование

Исследование, описанное в статье про топология, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое топология и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Общая топология

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.