§ 1. Предварительные сведения, обозначения.
Множества обозначаются: A, B, . . . (прописными буквами);
элементы множеств обозначаются: a, b, . . . (малыми буквами);
элемент a множества A обозначается: a ∈ A;
подмножество B множества A обозначается: B ⊂ A;
задание подмножества B множества A условием ϕ(X):
B = {x ∈ A : ϕ(X)}
(или B = {x : ϕ(X)}, если ясно о каком множестве A идет речь);
пустое множество обозначается: ∅ (договоренность: пустое множество не содержит элементов);
множества, элементами которых являются множества, называются семействами множеств и обозначаются: A, B, . . . (каллиграфическими буквами).
Пересечение множеств A и B: A ∩ B = {x : x ∈ A и x ∈ B};
множества A и B дизъюнктны, если A ∩ B = ∅;
объединение множеств A и B: A ∪ B = {x : x ∈ A или x ∈ B};
пересечение непустого семейства множеств A:
объединение непустого семейства множеств A:
Законы дистрибутивности:
Разность множеств A и B: A \ B = {x : x ∈ A и x 6∈ B}.
Законы де Моргана:
§ 2.
отображения множеств .
Упорядоченная пара (x, y) есть множество {{x}, {x, y}}, если x 6= y, и множество {x}, если
x = y. Декартово произведение множеств X и Y :
X × Y = {(x, y) : x ∈ X, y ∈ Y }.
Всякое подмножество произведения X × Y есть некоторое отношение. Отношение f ⊂ X × Y
называется отображением множества X в множество Y , если
1) для любого x ∈ X существует (x, y) ∈ f, и
2) из (x, y) ∈ f и (x, y0
) ∈ f следует, что y = y0.
Обозначение f : X → Y .
Для x ∈ X единственное y ∈ Y , для которого (x, y) ∈ f называется значением f в точке x и
обозначается f(x). Образ f(A) множества A ⊂ X при отображении f есть множество f(A) = {y ∈ Y : y = f(x) для некоторого x ∈ A}.
Прообраз f−1(B) множества B ⊂ Y при отображении f есть множество f−1 (B) = {x ∈ X : f(x) ∈ B}.
Для отображения f : X → Y и подмножества M ⊂ X отображение f, рассматриваемое только
на M, называется сужением (ограничением) отображения f на M и обозначается f|M. Получаем отображение f|M : M → Y , где (f|M)(x) = f(x).
Для отображений f : X → Y и g : Y → Z равенство (g ◦ f)(x) = g(f(x)), x ∈ X определяет композицию отображений f и g: (g ◦ f) : X → Z.
Отображение f : X → Y называется инъективным, если для любой пары точек x1, x2 ∈ X из f(x1) = f(x2) следует, что x1 = x2.
Отображение f : X → Y называется сюръективным или отображением “на”, если f(X) = Y .
Отображение f : X → Y , являющееся одновременно инъективным и сюръективным, называется биективным или взаимно однозначным.
Отображение f : X → Y называется обратимым, если существует такое отображение g : Y → X, что g ◦ f = idX и f ◦ g = idY , где idX (соответственно idY ) — тождественное отображение множества X (соответственно Y ) на себя. Отображение g называется обратным к f, однозначно определяется отображением f, и обозначается f−1
.
Для семейства множеств A сюръективное отображение f множества J на A называется индексирующим отображением. Семейство A с индексирующим отображением f : J → A называется индексированным семейством множеств. Обозначение: A = {Aα : α ∈ J}. Любое семейство
множеств A с тождественным индексирующим отображением id : A → A является индексированным семейством A = {AA : A ∈ A}. Объединение и пересечение индексированных семейств обозначаются:
соответственно.
Если J = {1, . . . , k} или J = N (N — натуральные числа), то объединения и пересечения
индексированных семейств обозначаются:
.
Семейство всех подмножеств множества A обозначается 2
A. Обоснование обозначения следующее. Для любого элемента B ∈ 2
A рассмотрим отображение fB : A → 2 = {0, 1} (характеристическую функцию подмножества B),
Элементы 2A находятся во взаимно однозначном соответствии с характеристическими функциями.
§ 3.
отношение эквивалентности .
Отношение R на множестве X, т.е. подмножество произведения X × X, называется отношением эквивалентности, если R удовлетворяет следующим свойствам (x ∼ y обозначает, что
(x, y) ∈ R):
1) x ∼ x для любого x ∈ X (рефлексивность),
2) x ∼ y ⇒ y ∼ x (симметричность),
3) x ∼ y, y ∼ z ⇒ x ∼ z (транзитивность).
Всякое отношение эквивалентности R на множестве X определяет разбиение X на попарно
непересекающиеся множества (классы эквивалентности отношения R): x, y в одном классе эквивалентности в том и только том случае, если x ∼ y. Класс эквивалентности элемента x ∈ X
обозначается через [x]. Множество всех классов эквивалентности отношения R обозначается
через X/R и называется фактормножеством множества X относительно R.
Обратно, всякое разбиение множества X на непересекающиеся множества, определяет на нем
единственное отношение эквивалентности, классы эквивалентности которого совпадают с исходным разбиением.
3.1. Примеры. Пусть f : X → Y сюръективное отображение. Определено отношение эквивалентности R на X: x ∼ y в том и только том случае, если f(x) = f(y). Классами эквивалентности отношения являются прообразы точек при отображении f. Определена естественная биекция X/R на Y .
Частными случаями данной конструкции являются: отображение проектирования плоскости
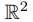
на ось Ox (классы эквивалентности — прямые параллельные оси Oy); отображение плоскости
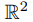
на неотрицательные вещественные числа
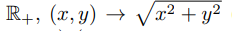
2 (точке плоскости ставится в соответствие ее расстояние до начала координат) (классы эквивалентности — окружности с центром в начале координат O и точка O).
3.2. Предложение. Пусть R — отношение эквивалентности на X и Y ⊂ X. Тогда ограничение R|Y отношения R на Y есть отношение эквивалентности.
§ 4.
упорядочение ,
линейное упорядочение ,
вполне упорядочение .
Пусть ≤ — отношение на множестве X. Говорят, что ≤ упорядочивает X или что ≤ является упорядочением (порядком) на X, если отношение ≤ удовлетворяет следующим свойствам:
1) Если x ≤ y и y ≤ z, то x ≤ z (транзитивность),
2) x ≤ x для всякого x ∈ X (рефлексивность),
3) Если x ≤ y и y ≤ x, то x = y (антисимметричность).
Множество X вместе с порядком ≤ на нем называется упорядоченным множеством. Обозначение (X, ≤). Два элемента x и y упорядоченного множества X называются несравнимыми, если никакое из неравенств x ≤ y и y ≤ x не выполняется.
4.1. Примеры. На плоскости
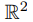
рассмотрим следующее отношение ≤:
(x1, x2) ≤ (y1, y2) ⇐⇒ x1 ≤ y1 и x2 ≤ y2. (4.1)
Легко видеть, что ≤ есть порядок на R2
. Для точки (x, y) множество точек {(a, b) : x ≤ a, y ≤ b}
есть квадрант ограниченный лучами, параллельными осям координат, и вершиной в (x, y) (множество точек {(a, b) : a ≤ x, b ≤ y} есть квадрант ограниченный лучами, параллельными осям координат и имеющими противоположное направление, и вершиной в (x, y)). Точки лежащие в
дополнение до этих двух квадрантов несравнимы с (x, y). Упорядочение на N: a ≤ b ⇐⇒ a|b (a делит b).
Говорят, что подмножество Y упорядоченного множества X имеет верхнюю грань в X, если существует элемент x ∈ X, для которого y ≤ x для всех y ∈ Y .
Элемент x упорядоченного множества X называется максимальным, если для любого другого элемента y ∈ X либо y ≤ x, либо y несравним с x. Элемент x ∈ X называется наибольшим, если y ≤ x для всех y ∈ X.
Аналогично определяются: нижняя грань подмножества, минимальный элемент и наименьший элемент упорядоченного множества.
4.2. Пример. Рассмотрим множество
с порядком, являющимся ограничением на X порядка на плоскости (4.1). Подмножество Y = �(x, −x) : x ∈ R
является множеством всех максимальных элементов упорядоченного множества X, и ни один из элементов Y не является наибольшим в X.
Упорядоченное множество (X, ≤) называется линейно упорядоченным, если оно не содержит несравнимых элементов, т.е. для x, y ∈ X всегда x ≤ y или y ≤ x. Если X линейно упорядочено отношением ≤, то, полагая для любых x, y ∈ X
x < y в том и только том случае, когда x ≤ y и x 6= y
получаем отношение линейного порядка <. Оно удовлетворяет следующим свойствам:
1) Если x < y и y < z, то x < z (транзитивность),
2) Если x < y, то отношение y < x не имеет места (антирефлексивность),
3) Если x 6= y, то либо y < x, либо x < y (сравнимость).
В линейно упорядоченном множестве понятия максимального и наибольшего (минимального и наименьшего) элементов совпадают.
4.3. Примеры. На плоскости R2 отношение (x1, x2) < (y1, y2) ⇐⇒ x1 < y1, или x1 = y1 и x2 < y2 является линейным порядком.
Пусть (X, <) и (Y, <) — линейно упорядоченные множества. Лексикографическим порядком на произведении X × Y называется линейный порядок:
(x1, y1) < (x2, y2), если x1 < x2 или x1 = x2 и y1 < y2.
Линейный порядок на произведении прямых — частный случай лексикографического порядка.
4.4. Предложение. Пусть (X, ≤) — упорядоченное множество и Y ⊂ X. Тогда отношение ≤ |Y есть отношение порядка на Y . Если ≤ есть линейный порядок на X, то ≤ |Y является линейным порядком на Y .
Линейный порядок < на множестве X называется вполне упорядочением, а множество X вместе с порядком < называется вполне упорядоченным, если каждое непустое подмножество множества X имеет наименьший элемент.
4.5. Примеры. Любое конечное линейно упорядоченное множество — вполне упорядочено.
Множество натуральных чисел N (с естественным порядком) — вполне упорядоченное множество.
Множество натуральных чисел с добавленным элементом N∪{∞} (на N естественный порядок, n < {∞} для любого n ∈ N) — вполне упорядоченное множество.
Множества целых чисел Z, вещественных чисел R (с естественными порядками) — не вполне упорядоченные множества.
Подмножество вполне упорядоченного множества — вполне упорядоченное множество.
Лексикографический порядок на произведении вполне упорядоченных множеств A и B — вполне упорядочение. Действительно, пусть X ⊂ A × B, pr : A × B → A — проекция. Обозначим через a0 наименьший элемент множества pr(X) ⊂ A. Тогда множество {b : (a0, b) ∈ X} ⊂ B имеет наименьший элемент b0. Элемент (a0, b0) будет наименьшим элементом множества X.
§ 5.
равномощность множеств .
мощность множества .
кардинальные числа . Теорема Кантора–Бернштейна.
Мощность множества — это в некотором смысле “количество” его элементов. Для конечного
множества с понятием количества его элементов не возникает никаких вопросов. С бесконечными
множествами ситуация сложнее.
Множества A и B называются эквивалентными или равномощными (обозначения: A ∼ B или
|A| = |B|), если существует биективное отображение f : A → B. Равномощность множеств —
отношение эквивалентности. Каждому множеству X приписывается кардинальное число (или
кардинал) |X| — мощность множества X. Равномощным множествам приписываются равные
кардинальные числа.
Множество называется счетным, если оно равномощно множеству натуральных чисел N. Его
мощность обозначается ℵ0.
Множество называется несчетным, если оно не конечно и не равномощно N.
Порядок на кардиналах. Если существует инъективное отображение множества A в B, то
|A| ≤ |B|. Если |A| ≤ |B| и множества A и B не эквивалентны, то |A| < |B|.
5.1. Теорема (существование не эквивалентных бесконечных множеств). Для любого множества
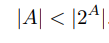
Доказательство. Отображение g : A → 2
A, g(a) = {a}, множества A на множество {{a} :a ∈ A} ⊂ 2
A всех одноточечных подмножеств A инъективно. Тем самым
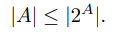
. (5.1)
Для завершения доказательства покажем, что не существует сюръективного отображения Aна 2
A. Пусть g : A → 2
A — произвольное отображение. Для любого a ∈ A множество g(a)
является подмножеством A либо содержащим a, либо его не содержащим. Положим
B = {a ∈ A : a 6∈ g(a)} (множество элементов A, образы которых себя не содержат).
Покажем, что B 6∈ g(A). Тогда g(A) 6= 2A.
Возьмем любое a ∈ A. Если a ∈ g(a) то, по определению множества B, a 6∈ B и, значит,
g(a) 6= B. Если a 6∈ g(a), то a ∈ B, и снова g(a) 6= B. Итак, для всех a ∈ A g(a) 6= B, т.е. B 6∈ g(A).
Значит
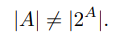
(5.2)
Из (5.1) и (5.2) имеем |A| < |2A|.
5.2. Следствие. Множество 2
N несчетно.
5.3. Предложение. Множество 2
N равномощно множеству точек отрезка I = [0, 1].
Доказательство. Множество 2
N естественно отождествляется с множеством последовательностей из 0 и 1. Двоичная запись
t = 0, i1i2 . . . ik . . .
произвольного числа t ∈ I = [0, 1] дает нам отображение f : 2N → I. Оно является сюръективным, но не взаимно однозначным. Числам вида
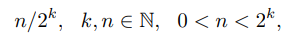
(5.3)
соответствуют в точности две записи: у одной, начиная с некоторого номера, все цифры равны
0, а у другой — все единицы. Обозначим через D множество двоично-рациональных чисел на отрезке I, т.е. множество чисел вида (5.3). На множестве f
−1 (I \D) отображение f инъективно. Но множества D и f −1(D) счетны. Значит, существует биекция g : f−1 (D) → D. Тогда отображение h : 2N → I, определяемое следующим образом:
,
является биекцией.
Мощностью континуума называется мощность отрезка I = [0, 1]. Она обозначается c.
5.4. Теорема (Кантор–Бернштейн) (антисимметричность порядка на кардиналах). Если
|A| ≤ |B| и |B| ≤ |A|, то |A| = |B|.
Доказательство. Пусть f : A → B0
, B0 ⊂ B, g : B → A0
, A0 ⊂ A, — биекции. Положим
Легко видеть, что
f(C) = D, g(D) = C \ C0.
Тогда отображение
h : A → B, где h|C = f, h|A\C = g
−1
является искомой биекцией.
§ 6.
ординалы .
Вполне упорядоченные множества (X, <) и (Y, <0) подобны, если существует биекция f множества X на Y , сохраняющая порядок, т.е. для любых x, y ∈ X, если x < y, то f(x) <0 f(y).
Подобие вполне упорядоченных множеств — отношение эквивалентности. Каждому вполне
упорядоченному множеству (X, <) приписывается порядковое число или ординал — порядковый
тип множества X. Порядковые типы вполне упорядоченных множеств (X, <) и (Y, <0) одинаковы в том и только том случае, когда множества (X, <) и (Y, <0) подобны.
Порядок на ординалах. Пусть α и β — ординалы, являющиеся порядковыми типами множеств (X, <) и (Y, <0) (с наименьшими элементами x0 и y0 соответственно). Положим α < β, если существует y ∈ Y такое, что X подобно начальному отрезку [y0, y) = {t ∈ Y : t <0 y}.
6.1. Замечание (свойства начальных отрезков). У конечного вполне упорядоченного множества из n элементов n − 1 начальный отрезок.
В бесконечном вполне упорядоченном множестве содержатся начальные отрезки из n элементов, n ∈ N.
Пусть X — вполне упорядоченное множество, [x0, x) — начальный отрезок X. Тогда или [x0, x) ∪ {x} = X, или [x0, x) ∪ {x} — начальный отрезок.
Объединение начальных отрезков вполне упорядоченного множества X или начальный отрезок, или само множество X.
Если ϕ задает подобие множеств X и Y , [x0, x) — начальный отрезок X, то ϕ|[x0,x) задает подобие [x0, x) и начального отрезка [y0, f(x)) в Y .
6.2. Предложение. Для любых двух различный ординалов α и β всегда имеет место один из случаев:
(1) α < β,
(2) α > β.
Доказательство. Случай, когда один из ординалов α или β конечен разобрать самостоятельно.
Пусть ординалы α и β являются порядковыми типами бесконечных множеств (X, <) и (Y, <0)
с наименьшими элементами x0 и y0 соответственно.
Пусть Z — множество пар (X0, Y 0) подобных начальных отрезков X и Y . Z 6= ∅.
Подобие начальных отрезков X0 и Y0 определяется однозначно множеством X0. В самом деле,
пусть существует два различных вложения: ϕ : X0 → Y и ϕ0
: X0 → Y , задающие подобие X0и начальных отрезков Y . Обозначим через x наименьший элемент множества X0
, такой, что ϕ(x) 6= ϕ0(x). Очевидно, что x 6= x0. Тогда ϕ|[x0,x) = ϕ0 |[x0,x) и
Из этого следует, что ϕ(x) = ϕ0(x). Противоречие.
Положим
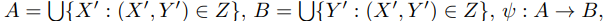
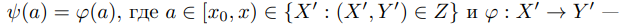
подобие.
Отображение ψ корректно определено (по факту из Замечания 6.1 и аргументу, приведенному
выше в доказательстве). Отображение ψ реализует подобие множеств A и B.
По факту из Замечания 6.1 A или начальный отрезок [x0, x), или A = X; B или начальный
отрезок [y0, y), или B = Y .
I Случай A = X, B = Y невозможен из-за предположения α 6= β.
II Случай A = X, B = [y0, y) соответствует неравенству α < β.
III Случай A = [x0, x), B = Y соответствует неравенству α > β.
IV Случай A = [x0, x), B = [y0, y). Положим A+ = A ∪ {x}, B+ = B ∪ {y}. Определено
отображение ψ
+ : A+ → B+, ψ
+|A = ψ, ψ
+(x) = y, реализующее подобие множеств A+ и B+.
Если A+ 6= X и B+ 6= Y , то A+ и B+ — подобные начальные отрезки. Но (A+, B+) 6∈ Z.
Противоречие.
Если A+ = X и B+ 6= Y , то α < β.
Если A+ 6= X и B+ = Y , то α > β.
Если A+ = X и B+ = Y , то X и Y — подобные множества. Противоречие с предположением
α 6= β.
Во всех случах или α < β, или α > β.
6.3. Теорема. Множество ординалов вполне упорядочено.
Доказательство. С учетом Предложения 6.2 множество ординалов линейно упорядочено.
Пусть A — подмножество ординалов, α — произвольный элемент A. Если α — наименьший
элемент A, то все доказано.
Иначе, пусть Yα — вполне упорядоченное множество, порякового типа α ∈ A (с наименьшим
элементом y0), A0 = {α
0 ∈ A : α
0 < α}, Yα0 — вполне упорядоченное множество, порякового типа
α
0 ∈ A0
.
Для любого α
0 ∈ A0
существует начальный отрезок [y0, yα0 ) в Yα, подобный Yα0 . Положим
yα0 = inf{yα0 : α
0 ∈ A0}. Тогда α0 — наименьший элемент A.
Одно из главных назначений вполне упорядоченных множеств — служить основой доказательств по трансфинитной индукции. Принцип трансфинитной индукции, обобщающий обычный принцип математической индукции, заключается в следующем.
Теорема (принцип трансфинитной индукции). Пусть (W, <) — вполне упорядоченное множество, и каждому α ∈ W поставлено в соответствие некоторое утверждение P(α), причем
так, что выполняются следующие два условия:
(1) утверждение P(0) верно, где 0 — первый элемент множества (W, <);
(2) если β ∈ W и P(α) верно для всех α < β, α ∈ W, то P(β) тоже верно.
Тогда P(α) верно при всех α ∈ W.
§ 7.
аксиома выбора . Лемма Куратовского–Цорна.
теорема цермело . Вполне упорядоченность кардиналов.
Аксиома выбора. Для каждого семейства {Xα : α ∈ J} непустых множеств существует
такое отображение f : J →S
α∈J Xα, что f(α) ∈ Xα для каждого α ∈ J.
Лемма Куратовского–Цорна. Пусть (X, ≤) — упорядоченное множество. Предположим, что каждое линейно упорядоченное подмножество Y ⊂ X имеет верхнюю грань в X. Тогда X имеет максимальный элемент.
Теорема Цермело. На каждом множестве X существует отношение <, которое вполне упорядочивает X.
Лемма Куратовского–Цорна, Теорема Цермело и аксиома выбора эквивалентны.
Вполне упорядоченность кардиналов. Пусть α и |X| — ординал и кардинал, для множества X, β и |Y | — ординал и кардинал, для множества Y . Выбор ординалов возможен по Теореме
Цермело. Выбор не однозначен. Нам подойдут произвольно выбранные ординалы.
Если α ≤ β, то |X| ≤ |Y | (если существует подобие α на начальный отрезок β или α и β
подобны, то существует инъекция X в Y ). Значит кардиналы сравнимы.
Если |X| < |Y |, то α < β (если не существует инъекции Y в X, то α и β не подобны и не
существует подобия β на начальный отрезок α). Последнее условие позволяет рассматривать
множество кардиналов как подмножество ординалов (с согласованными порядками). А именно,
каждому кардиналу κ ставится в соответствие произвольный порядковый тип (ординал) множества, мощности κ. Тем самым кардиналы — вполне упорядоченное множество (как подмножество ординалов).
7.1. Пример. Существует вполне упорядоченное множество T с максимальным элементом ω1
(и наименьшим элементом t0) такое, что начальный отрезок [t0, ω1) = {t ∈ T : t < ω1} несчетен,
а начальные отрезки [t0, y) = {t ∈ T : t < y}, y < ω1, счетны.
Возьмем несчетное вполне упорядоченное множество A (с наименьшим элементом a) и рассмотрим лексиграфически упорядоченное произведение {0, 1}×A (с порядком 0 < 1 на двоеточии
{0, 1}). Начальный отрезок [(0, a),(1, a)) несчетен. Пусть c — наименьший элемент {0, 1}×A, для
которого начальный отрезок [a, c) несчетен. Он существует, так как множество {0, 1} × A с лексиграфическим порядком вполне упорядочено. Тогда подмножество T = [a, c) ∪ {c} является
искомым.
Множество T(ω1) = T \ {ω1} называется множеством счетных трансфинитов. Его мощность
обозначается ℵ1.
Равенство 2
ℵ0 = ℵ1 называется гипотезой континуума. Обобщенная
гипотеза континуума
утверждает, что для любого бесконечного множества X, не существует множества Y мощности
меньше 2
X и больше X. Они независимы от аксиом теории множеств.
Задание N 1
1. Проверьте выполнение равенств: для A, B, C ⊂ X
(a) A ∩ (B \ C) = (A ∩ B) \ (A ∩ C);
(b) A ∪ (B \ C) = (A ∪ B) \ (A ∪ C);
для A, C ⊂ X, B, D ⊂ Y
(c) (A × B) ∩ (C × D) = (A ∩ C) × (B ∩ D);
(d) (A × B) ∪ (C × D) = (A ∪ C) × (B ∪ D);
(e) (A \ C) × (B \ D) = (A × B \ C × B) \ A × D;
(f) (A × B) \ (C × D) = (A \ C) × (B \ D).
2. Пусть X0 ⊂ X, Y0 ⊂ Y и f : X → Y . Докажите, что
10
(a) X0 ⊂ f
−1
(f(X0)) и равенство выполняется если f инъективно;
(b) f(f
−1
(Y0)) ⊂ Y0 и равенство выполняется если f сюръективно.
3. Пусть X0, X1 ⊂ X, Y0, Y1 ⊂ Y и f : X → Y . Докажите, что:
(d)
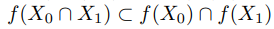
и равенство выполняется если отображение инъективно;
(e)
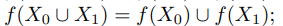
(f)
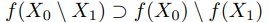
и равенство выполняется если отображение инъективно.
4. Пусть
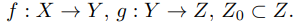
. Докажите, что
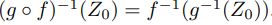
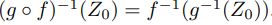
.
5. Пусть f : X → Y , g : Y → Z и отображение g ◦ f инъективно (сюръективно). Докажите, что f инъективно (g сюръективно).
6. Докажите, что отображение обратимо в том и только том случае, если оно биективно.
7. Пусть R — отношение эквивалентности на X и Y ⊂ X. Докажите, что ограничение R|Y отношения R на Y есть отношение эквивалентности.
8. Пусть на плоскости
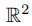
дано подмножество
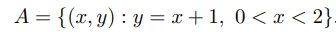
Описать отношение эквивалентности на прямой R, которое является пересечением всех отношений эквивалентности, содержащих множество A (т.е. наименьшее отношение эквивалентности на R, содержащее множество A).
9. Будет ли упорядочением на Z (целые числа) отношение: a ≤ b в том и только случае, если a|b (a делит b)?
10. Будет ли упорядочением на 2A (семействе всех подножеств множества A) отношение: B ≤ C в том и только случае, если B ⊂ C?
11. Пусть (X, ≤) — упорядоченное множество и Y ⊂ X. Докажите, что отношение ≤ |Y есть отношение порядка на Y , если ≤ есть линейный порядок на X, то ≤ |Y является линейным порядком на Y .
12. Докажите, что множества {0, 1} × N и N × {0, 1} с лексикографическим порядком не подобны.
13. (а) Докажите, что у конечного вполне упорядоченного множества из n элементов n − 1
начальный отрезок.
(б) Докажите, что в бесконечном вполне упорядоченном множестве содержатся начальные
отрезки из n элементов, n ∈ N.
(в) Пусть X — вполне упорядоченное множество, [x0, x) — начальный отрезок X. Докажите,
что тогда или [x0, x) ∪ {x} = X, или [x0, x) ∪ {x} — начальный отрезок.
(г) Докажите, что объединение начальных отрезков вполне упорядоченного множества X или
начальный отрезок, или само множество X.
(д) Докажите, что если ϕ задает подобие множеств X и Y , [x0, x) — начальный отрезок X, то
ϕ|[x0,x) (ограничение ϕ на [x0, x)) задает подобие [x0, x) и начального отрезка [y0, f(x)) в Y .
14. Докажите, что единственным подобием на себя вполне упорядоченного множества является тождественное отображение.
15. Доказать, что для любого непустого множества X существует биекция XN × XN на XN (где XN — множество отображений из N в X).
16. Доказать, что произведение Nn счетно при любых n ∈ N. Доказать, что произведение N N (или множество отображений из N в N) имеет мощность континуума.
17. Найти мощность множества

(множества отображений из
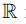
в
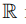
).
Дополнительные задачи Задания N 1
18. Докажите, что на N
N отношение (a1, a2, . . .) < (b1, b2, . . .) в том и только том случае, если
ai = bi для i < n и an < bn, является линейным, но не вполне упорядочением.
19. (a) Докажите, что линейно упорядоченное множество A не является вполне упорядоченным в том и только том случае, если A содержит множество, подобное последовательности
{−n : n ∈ N}.
(b) Докажите, что линейно упорядоченное множество A вполне упорядочено в том и только
том случае, если его любое счетное подмножество вполне упорядочено.
20. (а) Найдите мощность всех конечных подмножеств бесконечного множества X.
(б) Найдите мощность всех счетных подмножеств бесконечного множества X.
21. Пусть X — бесконечное множество. Докажите, что множества X × X и X равномощны.
22. (а) Какая мощность множества всех порядковых типов конечного множества?
(б) Какая мощность множества всех порядковых типов счетного множества?
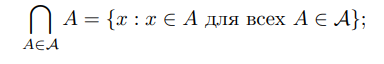
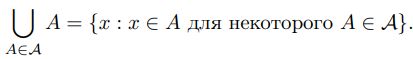
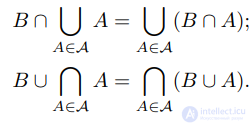
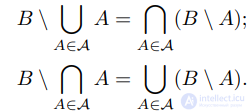
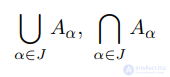
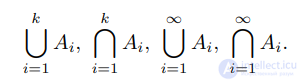
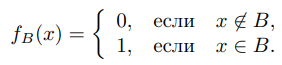
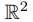 на ось Ox (классы эквивалентности — прямые параллельные оси Oy); отображение плоскости
на ось Ox (классы эквивалентности — прямые параллельные оси Oy); отображение плоскости 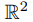 на неотрицательные вещественные числа
на неотрицательные вещественные числа 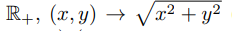 2 (точке плоскости ставится в соответствие ее расстояние до начала координат) (классы эквивалентности — окружности с центром в начале координат O и точка O).
2 (точке плоскости ставится в соответствие ее расстояние до начала координат) (классы эквивалентности — окружности с центром в начале координат O и точка O).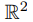 рассмотрим следующее отношение ≤:
рассмотрим следующее отношение ≤: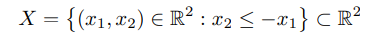
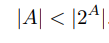
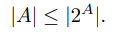 . (5.1)
. (5.1)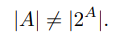 (5.2)
(5.2)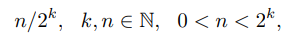 (5.3)
(5.3)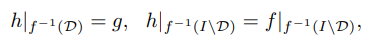
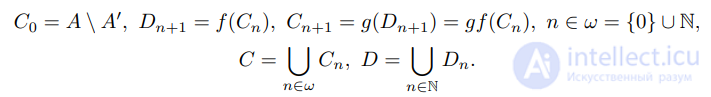
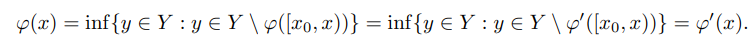
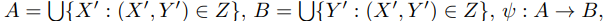
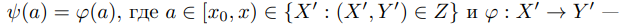 подобие.
подобие.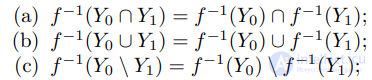
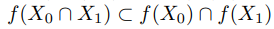 и равенство выполняется если отображение инъективно;
и равенство выполняется если отображение инъективно;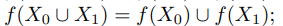
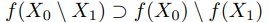 и равенство выполняется если отображение инъективно.
и равенство выполняется если отображение инъективно.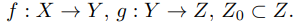 . Докажите, что
. Докажите, что 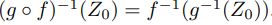
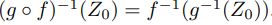 .
.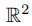 дано подмножество
дано подмножество 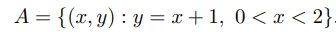
 (множества отображений из
(множества отображений из 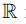 в
в 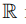 ).
).
Комментарии
Оставить комментарий
Общая топология
Термины: Общая топология