Лекция
Это продолжение увлекательной статьи про постоянный электрический ток.
...
style="text-align:right">(4.37)
Подставим (4.37) в (4.36):
|
|
(4.38) |
Мы видим, что у этого уравнения имеется стационарное решение (постоянный заряд на конденсаторе)

При таком заряде на конденсаторе напряжение на нем равно ЭДС источника тока, и ток по цепи не идет

Введем отклонение у заряда на конденсаторе от его стационарного значения
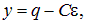
или

Подставляя это соотношение в (4.38), находим уравнение для функции y(t)
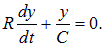
Это уравнение легко интегрируется

откуда
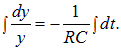
Вычисляя интегралы. находим

или

где y0 — произвольная постоянная интегрирования (значение у в начальный момент времени). Отсюда находим заряд на конденсаторе
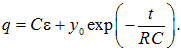
Нам осталось использовать начальное условие: в момент t = 0 конденсатор был не заряжен
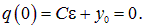
Отсюда находим
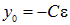
и окончательно
|
|
(4.39) |
Дифференцируя q(t) по времени, находим ток в цепи
|
|
(4.40) |
Напряжение на конденсаторе U(t) = q(t)/C без труда получается из (4.39)
|
|
(4.41) |
Таким образом, по мере роста заряда и напряжения на конденсаторе ток в цепи уменьшается. При этом заряд конденсатора стремится к своему стационарному значению 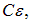 а напряжение на конденсаторе — к ЭДС источника тока. Величина
а напряжение на конденсаторе — к ЭДС источника тока. Величина  имеет размерность времени и определяет характерное время процесса зарядки. За промежуток
имеет размерность времени и определяет характерное время процесса зарядки. За промежуток  ток в цепи уменьшается
ток в цепи уменьшается
в е = 2,72 раза.
На рис. 4.21 показана зависимость заряда на конденсаторе и тока в цепи для конкретных значений R = 1,5 кОм, С = 2 мкФ, 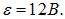 Характерное время процесса равно при этих значениях
Характерное время процесса равно при этих значениях 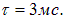 Из рисунков видно, что уже при временах порядка
Из рисунков видно, что уже при временах порядка

конденсатор почти полностью заряжается.

Рис. 4.21. Графики зависимости напряжения на конденсаторе (слева) и тока в цепи (справа)
при зарядке конденсатора емкостью С = 2 мкФ через активное сопротивление R = 1,5 кОм от источника тока с ЭДС 12 В
Рассмотрим теперь процесс разрядки конденсатора. Зарядив его до какого-то заряда  (или, что то же самое, до начального напряжения U0 = q0/C), мы перебрасываем переключатель в положение b (см. рис. 4.20). Конденсатор начнет разряжаться, а по цепи пойдет ток. Мы имеем те же самые уравнения за исключением того, что в цепь не включен источник тока. Поэтому в этом случае надо положить
(или, что то же самое, до начального напряжения U0 = q0/C), мы перебрасываем переключатель в положение b (см. рис. 4.20). Конденсатор начнет разряжаться, а по цепи пойдет ток. Мы имеем те же самые уравнения за исключением того, что в цепь не включен источник тока. Поэтому в этом случае надо положить 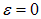 в уравнении (4.38). Тогда оно совпадет с тем, что мы ранее решали для y(t), поэтому решения для процесса разрядки конденсатора нам уже известны
в уравнении (4.38). Тогда оно совпадет с тем, что мы ранее решали для y(t), поэтому решения для процесса разрядки конденсатора нам уже известны
|
|
(4.42) |
Все эти величины быстро уменьшаются с течением времени: за тот же характерный промежуток  заряд конденсатора, напряжение на нем и ток в цепи падают в 2,72 раза. Отрицательный знак в выражении для тока означает, что ток при разрядке течет в направлении, обратном току при зарядке конденсатора.
заряд конденсатора, напряжение на нем и ток в цепи падают в 2,72 раза. Отрицательный знак в выражении для тока означает, что ток при разрядке течет в направлении, обратном току при зарядке конденсатора.
На практике очень часто встречаются сложные (разветвленные) электрические цепи, для расчета которых удобно использовать правила Кирхгофа (рис. 4.22).

Рис. 4.22. Г. Кирхгоф (1824–1887) — немецкий физик
Первое правило Кирхгофа является следствием закона сохранения заряда и того естественного требования, чтобы при стационарных процессах ни в одной точке проводника не накапливались и не уменьшались заряды. Это правило относится к узлам, то есть к таким точкам в разветвленной цепи, в которой сходится не менее трех проводников.
Первое правило Кирхгофа гласит:
|
Алгебраическая сумма токов, сходящихся в узле, равна нулю, то есть количество зарядов, приходящих в данную точку цепи в единицу времени, равно количеству зарядов, уходящих из данной точки за то же время
|
При этом токи, подходящие к узлу и отходящие от него, имеют противоположные знаки (рис. 4.23).

Рис. 4.23. Сумма токов, сходящихся в узле равна нулю
Второе правило Кирхгофа является обобщением закона Ома и относится к любому замкнутому контуру разветвленной цепи.
Второе правило Кирхгофа гласит:
|
В любом замкнутом контуре цепи алгебраическая сумма произведений токов на сопротивления соответствующих участков контура равна алгебраической сумме ЭДС в контуре (рис. 4.24)
|
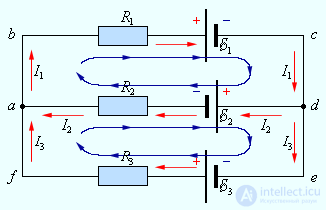
Рис. 4.24. Пример разветвленной электрической цепи.
Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)
Правила Кирхгофа позволяют определить силу и направление тока в любой части разветвленной цепи, если известны сопротивления ее участков и включенные в них ЭДС. Число уравнений, составляемых по первому и второму правилам Кирхгофа, должно равняться числу искомых величин. Используя первое правило Кирхгофа для разветвленной цепи, содержащей m узлов и n ветвей (участков), можно написать (m – 1) независимых уравнений, а используя второе правило, (n – m + 1) независимых уравнений.
Приведем пример расчета токов в разветвленной цепи (рис. 4.25).
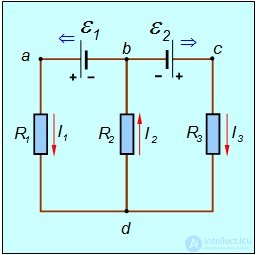
Рис. 4.25. Пример разветвленной цепи
Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I1, участок b–d с током I2 и участок b–c–d с током I3 (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике?
Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным. В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25).
Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла b, куда входит ток I2 и выходят токи I1 и I3
|
|
(4.45) |
Шаг третий. Нам осталось написать уравнения (в нашем случае - два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.
Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока, I1 и I2, направления которых совпадают с выбранным направлением обхода. ЭДС 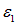 также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как
также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как
|
|
(4.46) |
В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока I1 и I3, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых  войдет в уравнения со знаком плюс, а
войдет в уравнения со знаком плюс, а 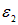 — со знаком минус. Уравнение для этого замкнутого пути имеет вид
— со знаком минус. Уравнение для этого замкнутого пути имеет вид
|
|
(4.47) |
Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I3 через I1 из уравнения (4.47)
|
|
(4.48) |
I2 через I1 с помощью уравнения (4.46)
|
|
(4.49) |
и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное I1, которое находится без труда
|
|
(4.50) |
Подставляя это выражение в (4.48), (4.49), находим соответственно токи I2, I3
|
|
(4.51) |
Шаг пятый. В найденные формулы подставляют численные значения, коль скоро они заданы. Подсчитаем для примера токи в нашей цепи при одинаковых сопротивлениях R1 = R2 = R3 = 10 Ом, но разных ЭДС 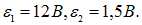 Имеем:
Имеем:
|
|
(4.52) |
Последнее значение получилось отрицательным при данных численных характеристиках цепи. Значит, на самом деле направление тока обратно показанному на рисунке. Это естественно: мощный левый источник посылает ток 0,75 А, часть которого (0,45 А) ответвляется в среднюю ветвь, а остаток — 0,3 А — продолжает течь в том же направлении, чему не может воспрепятствовать маломощная правая батарея.
Примечание. Правила Кирхгофа позволяют в принципе рассчитать сколь угодно сложные цепи. Но вычисления могут быть довольно сложными. Поэтому рекомендуется сначала поискать возможную симметрию цепи. Иногда из соображений симметрии более или менее очевидно, что какие-то токи равны между собой или какие-то напряжения равны нулю (и тогда данный участок цепи можно исключить из рассмотрения). Если такое возможно, вычисления существенно упрощаются.
В нашем примере мы пренебрегли внутренним сопротивлением источников тока. При их наличии они также должны включаться в уравнения второго правила Кирхгофа.
Пример. Два одинаковых источника тока с ЭДС 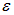 и внутренним сопротивлением r соединяются в батарею. Возможны два варианта соединения — последовательное и параллельное (рис. 4.26). При каком соединении ток в нагрузке R будет наибольшим?
и внутренним сопротивлением r соединяются в батарею. Возможны два варианта соединения — последовательное и параллельное (рис. 4.26). При каком соединении ток в нагрузке R будет наибольшим?
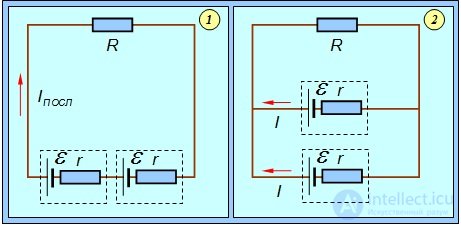
Рис. 4.26. Последовательное (1) и параллельное (2) соединение источников тока
Решение. Расчет особенно прост для последовательного соединения: уравнение первого правила Кирхгофа отсутствует, так как в цепи нет узлов. Единственное уравнение второго закона дает
|
|
(4.53) |
Для упрощения расчета параллельного соединения примем во внимание, что из соображений симметрии токи через источники должны быть равны и совпадать по направлению. Тогда первое правило Кирхгофа дает
|
|
(4.54) |
Второе правило Кирхгофа, записанное для пути через нижний источник и нагрузку, имеет вид
|
|
(4.55) |
Отсюда следует, что
|
|
(4.56) |
Сравнивая (4.53) и (4.56), находим, что при R > r ток последовательной батареи больше (Iпосл > Iпарал) а при R < r он меньше (Iпосл < Iпарал) тока от параллельной батареи. При равенстве внутреннего сопротивления и нагрузки R = r обе батареи дают одинаковый ток.
Предположим, что на концах участка проводника имеется разность потенциалов 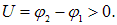 Перемещаясь из точки 2 с большим потенциалом в точку 1, где потенциал меньше, положительный заряд
Перемещаясь из точки 2 с большим потенциалом в точку 1, где потенциал меньше, положительный заряд 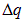 теряет энергию
теряет энергию
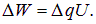
По определению для постоянного тока

тогда
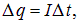
и теряемая энергия (или работа сил электрического поля) равна

Куда же девается эта энергия? Она не переходит в кинетическую энергию заряда, так как при постоянном токе дрейфовая скорость зарядов неизменна. Вспомним, что заряд не ускоряется из-за столкновений с атомами кристаллической решетки проводника. Значит, если в проводнике течет ток и проводник неподвижен, то работа сил электрического поля расходуется на нагревание проводника. Сталкиваясь с частицами проводника, носитель заряда передает им свою энергию, которую получает от поля. Поэтому работа поля над зарядами переходит, в конечном счете, в энергию теплового (хаотического) движения атомов проводника, то есть происходит нагревание проводника (рис. 27, 28, 29).

Рис. 4.27. Выделение теплоты в электрическом разряде

Рис. 4.28. Выделение теплоты в сопротивлении и лампе накаливания

Рис. 4.29. Выделение теплоты в нагревательном элементе
Видео 4.7. Выделение тепла в последовательно соединенных проводниках с разным удельным сопротивлением.
Таким образом, работа А, произведенная за время 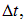 выделяется в проводнике в виде теплоты
выделяется в проводнике в виде теплоты 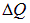
|
|
(4.57) |
Данная формула носит название закона Джоуля — Ленца. Закон установлен Дж. Джоулем в 1841 г. (рис. 4.30) и независимо от него русским физиком Э.X. Ленцем в 1842 г.

Рис. 4.30. Д. Джоуль (1818–1889) — английский физик
Пример. Пусть конденсатор емкостью С, заряженный до разности потенциалов U, разряжается через сопротивление R. Найти полное количество теплоты, выделившееся на нагрузке (рис. 4.31).
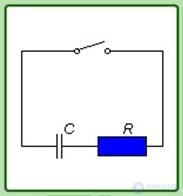
Рис. 4.31. Электрическая цепь с заряженным конденсатором и сопротивлением
Решение. В (4.42) мы нашли ток разрядки как функцию времени. Подставляем его в (4.57) и интегрируем по t.
Как и следовало ожидать, в теплоту перешла вся энергия электрического поля, запасенная первоначально в конденсаторе.
Количество теплоты, выделяемой в единицу времени (то есть тепловая мощность Р), равно
|
|
(4.58) |
Тепло выделяется по всему объему проводника. Найдем плотность тепловой мощности, то есть мощность, выделяемую в единице объема. Представим себе линейный проводник с постоянным сечением S и длиной l. Тогда напряжение на концах проводника можно выразить через напряженность электрического поля в нем
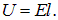
С другой стороны, сопротивление проводника равно

(напомним, что 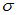 — проводимость данного вещества, обратная его удельному сопротивлению
— проводимость данного вещества, обратная его удельному сопротивлению 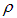 ). Отсюда находим
). Отсюда находим
|
|
(4.59) |
Таким образом, плотность тепловой мощности равна
|
|
продолжение следует...
Часть 1 Постоянный электрический ток Сила тока, напряжение ,ЭДС, законы и правила
Часть 2 4.4. Зарядка конденсатора - Постоянный электрический ток Сила тока, напряжение
Часть 3 4.5. Правила Кирхгофа - Постоянный электрический ток Сила тока, напряжение
Часть 4 4.7. Классическая теория - Постоянный электрический ток Сила тока, напряжение
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика