Лекция
Это продолжение увлекательной статьи про постоянный электрический ток.
...
src="/th/25/blogs/id8829/2eb71ed6562ede340ad9c643164f2022.png" data-auto-open loading="lazy" alt="Постоянный электрический ток Сила тока, напряжение ,ЭДС, законы и правила" >v =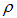 
at. Однако внутри проводника свободные заряды испытывают столкновения с атомами проводника. За время свободного полета t между двумя столкновениями заряд в проводнике приобретает скорость вдоль внешнего электрического поля
|
|
(4.16) |
После очередного столкновения направленная скорость теряется. Затем, до следующего столкновения, происходит новое наращивание направленной скорости. Поэтому в среднем направленная скорость движения постоянна и определяется скоростью, накапливаемой между двумя последовательными столкновениями.
На участке электрической линейной цепи длиной dl напряженность поля связана с потенциалом обычным соотношением
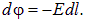
Следовательно, можно записать
|
|
(4.17) |
Видео 4.1. Демонстрация падения потенциала вдоль проводника, по которому идет ток.
Здесь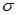 
и S — проводимость и площадь поперечного сечения проводника в том месте, где находится выбранный нами бесконечно малый элемент dl. А вот сила тока I будет постоянна на всей длине l проводника: при стационарном течении зарядов сколько их входит через одно сечение проводника, столько и выходит через другое. Это — также следствие закона сохранения заряда и предполагаемой стационарности ситуации, когда, в частности, 
.
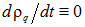В силу одинаковости силы постоянного тока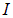 
через любое сечение проводника, при интегрировании соотношения (4.17) вдоль проводника от точки 1 до точки 2, мы можем вынести 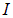за знак интеграла:
|
|
(4.18) |
Под знаком интеграла находится величина, не зависящая от величины силы тока и напряжения на концах проводника, но лишь от его геометрических размеров, формы и материала. Она называется сопротивлением проводника между точками 1 и 2
|
|
(4.19) |
где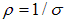 
— удельное сопротивление проводника.
Таким образом, получаем
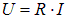
В случае прямолинейного однородного проводника постоянного сечения его сопротивление будет равно
|
|
(4.20) |
|
В СИ единицей измерения сопротивления является ом (Ом):
|
1 Ом — это сопротивление такого участка цепи без ЭДС, по которому протекает ток в 1 А при напряжении на его концах в 1 В (рис. Об этом говорит сайт https://intellect.icu . 4.8).
|
В СИ единицей измерения удельного сопротивления является ом · метр (Ом · м):
|
Рис. 4.8. Г. Ом (1787–1854) — немецкий физик
Удельное сопротивление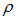 
вещества характеризует проводящую способность материала, оно различно для разных веществ и существенно зависит от температуры проводника. Однако 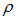не зависит от формы и размеров проводника. Мы не вынесли 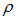за знак интеграла в (4.19), потому что встречаются цепи, отдельные участки которых составлены из различных материалов. В этом случае 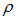будет зависеть от переменной интегрирования 
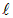. Значения удельного сопротивления для некоторых веществ приведены в таблице.
Таблица
Удельные сопротивления некоторых проводников
|
Проводники |
А1 |
Ag |
Сu |
Аu |
W |
Fe |
Нихром |
|
r (мкОм · м)
|
0,028 |
0,016 0,017 |
0,022 |
0,055 0,098 |
1,12 |
||
Обращает внимание, что в целом удельные сопротивления металлов близки друг к другу, что свидетельствует об общности механизма проводимости. Удельные же сопротивления плохих проводников и изоляторов варьируются в широких пределах. Например, для морской воды r = 0,3 Ом · м, для влажной земли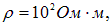 
для стекла 
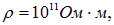для янтаря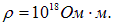 
Полученное выше соотношение
|
|
(4.21) |
называется законом Ома в интегральной форме (рис. 4.9) для однородного участка цепи, то есть участка, на котором нет источников — источников сторонних сил, или просто законом Ома (для такого участка цепи).
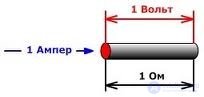
Рис. 4.9. Размерности физических величин в законе Ома
Пример 1. Проводник из меди имеет форму усеченного конуса с радиусами оснований r1 = 1 мм и r2 = 2 мм. Длина проводника L = 10 см. Найти его сопротивление.
Решение. Зависимость радиуса проводника r(l) от расстояния l, отсчитываемого от меньшего основания, показана на рис. 4.10.
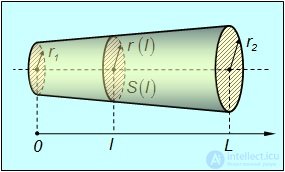
Рис. 4.10. К вычислению сопротивления проводника конической формы
Математически эта зависимость выражается линейным законом
|
|
(4.22) |
Площадь сечения S(l) на расстоянии l от левого конца можно найти как
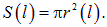
Тогда из формулы (4.19) следует
|
|
(4.23) |
Подставляя численные значения, находим
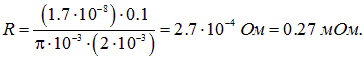
На практике электрические цепи представляют собой совокупность проводников, соединенных между собой определенным образом. Наиболее часто встречаются последовательное и параллельное сопротивление проводников.
Последовательное соединение проводников
|
Последовательным называется соединение проводников, при котором они включаются поочередно один за другим. |
При последовательном соединении согласно закону сохранения заряда через сопротивления проходит одинаковый заряд за одно и то же время, поэтому токи во всех сопротивлениях одинаковы
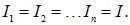
Падения напряжения на первом проводнике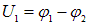 
на втором 
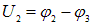и т.д. (рис. 4.11).
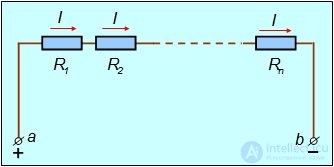
Рис. 4.11. Последовательное соединение проводников
Сумма падений напряжения на всех сопротивлениях равна напряжению Uab на концах цепи
|
|
(4.24) |
По закону Ома для участка цепи запишем
|
|
(4.25) |
Таким образом
|
|
(4.26) |
С другой стороны, Uab = IRпосл, где Rпосл — общее сопротивление цепи при последовательном соединении. Следовательно,
|
|
(4.27) |
Сводя воедино полученные соотношения, получаем закон последовательного соединения проводников:
|
При последовательном соединении проводников: — сила тока во всех проводниках одинакова и равна силе тока во всей цепи
— падение напряжения на всей цепи равно сумме падений напряжений на отдельных проводниках
— сопротивление цепи равно сумме сопротивлений отдельных проводников, входящих в цепь |
Параллельное соединение проводников
|
Параллельным называется соединение проводников, при котором их начала соединены вместе и их концы соединены вместе. |
При параллельном соединении (рис. 4.12) напряжение Uab на участке ab будет одинаковым для каждого отдельного сопротивления, то есть
|
|
(4.28) |
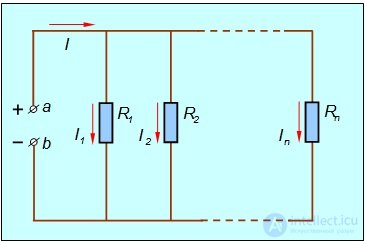
Рис. 4.12. Параллельное соединение проводников
Из закона сохранения заряда следует, что при разветвлении цепи часть зарядов может пойти по ее отдельным участкам, но полное количество заряда, пришедшего к точке разветвления, должно равняться сумме всех зарядов, вышедших из нее. Иными словами, ток I равен сумме токов в отдельных ветвях цепи
|
|
(4.29) |
С другой стороны, сила тока на всем участке равна
|
|
(4.30) |
где Rпap — общее сопротивление цепи при параллельном соединении.
Следовательно,
|
|
(4.31) |
Сводя воедино полученные соотношения, получаем закон параллельного соединения проводников:
|
При параллельном соединении проводников: — падение напряжения на каждом проводнике одинаково и равно падению напряжения во всей цепи
— сила тока в неразветвленной цепи равна сумме токов в отдельных проводниках
— сопротивление цепи равно
|
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 4.13 приведен пример такой сложной цепи и указана последовательность вычислений.
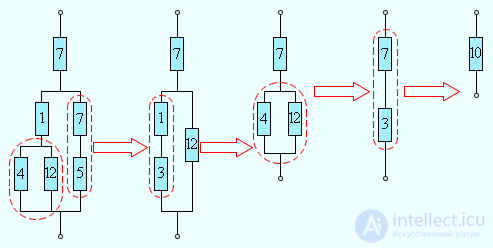
Рис. 4.13. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом)
Цепи, подобные изображенной на рис. 4.14, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
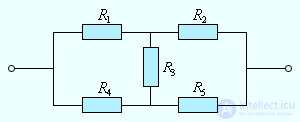
Рис. 4.14. Пример электрической цепи, которая не сводится к
комбинации последовательно и параллельно соединенных проводников
Как следует из (4.14), работа против сил поля внутри источника тока выражается через падение напряжения на внешнем сопротивлении R
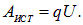
Для замкнутой электрической цепи работа против сил сопротивления среды источника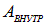 
приводит к падению напряжения 
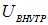внутри источника, так что
|
|
(4.32) |
Приписав источнику тока внутреннее сопротивление r, записываем падение напряжения на внутреннем участке цепи в соответствии с законом Ома
|
|
(4.33) |
Как следует из (4.13), при замкнутой внешней цепи (рис. 4.15, 4.16) ЭДС источника тока e равна сумме падений напряжения на внутреннем сопротивлении источника и во внешней цепи
|
|
(4.34) |
откуда
|
|
(4.35) |
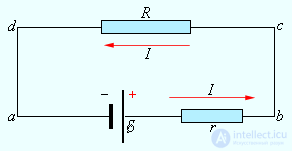
Рис. 4.15. Направление электрического тока J (1 → 2)
совпадает с направлением действия источника тока с ЭДС e (3 → 4)
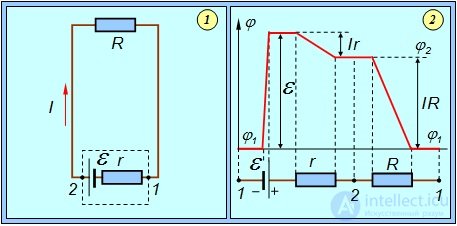
Рис. 4.16. Замкнутая цепь с активным сопротивлением R и источником тока (показан пунктирным прямоугольником) с ЭДС e и внутренним сопротивлением r. Напряжение на зажимах источника (точки 1 и 2) равно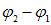 
и меньше ЭДС на величину падения напряжения Ir на внутреннем сопротивлении. Распределение потенциала вдоль цепи показано справа. Сумма падений напряжения на внутреннем сопротивлении и нагрузке (внешней цепи) равна ЭДС источника тока
Видно, что внешнее и внутреннее сопротивления можно рассматривать как два сопротивления, соединенных последовательно. На рис. 4.17 дано схематическое изображение источника постоянного тока с ЭДС равной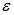 
и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность 
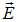электрического поля внутри батареи и силы, действующие на положительные заряды: 
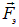— электрическая сила и 
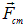— сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
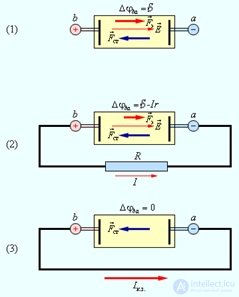
Рис. 4.17. Схематическое изображение источника постоянного тока:
1 — батарея разомкнута; 2 — батарея замкнута на внешнее сопротивление R; 3 — режим короткого замыкания
Измерительные приборы — вольтметры и амперметры — бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений (рис. 4.18).
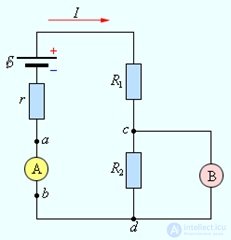
Рис. 4.18. Включение амперметра (А) и вольтметра (В) в электрическую цепь
На рис. 4.19 показан опыт по изучению падения напряжения на участке цепи. Падение напряжения на участке цепи, содержащем источник ЭДС, зависит от тока, протекающего по этому участку, и может даже менять знак при изменении этого тока. Это демонстрируется на примере цепи, в которую включены последовательно две батареи, реостат и амперметр. К одной из батарей подключен вольтметр, показывающий падение напряжения на ней. При изменении тока в цепи при помощи реостата величина и знак этого напряжения меняются.
Рис. 4.19. Опыт по изучению падения напряжения на участке цепи
В этом разделе мы решим задачи о зарядке и разрядке конденсатора. Электрическая цепь показана на рис. 4.20. Переключатель S позволяет подсоединять и отсоединять источник тока.
|
Рис. 4.20. Цепь для зарядки и разрядки конденсатора Пусть сначала конденсатор емкостью С не заряжен, и мы перебрасываем выключатель в положение а. По цепи пойдет зависящий от времени ток I(t), переносящий положительный заряд на верхнюю пластину конденсатора. Отметим, что хотя ток зарядки и разрядки конденсатора не является постоянным, но рассматривается здесь, поскольку его изменение в данном случае можно считать медленным. Обозначим заряд на этой пластине в момент t через q(t). Напряжение на конденсаторе можно найти как разницу между ЭДС и падением напряжения на нагрузке, то есть
Согласно закону сохранения заряда, изменение заряда q на обкладках конденсатора происходит только из-за наличия тока I. Поэтому второе уравнение процесса имеет вид
|
продолжение следует...
Часть 1 Постоянный электрический ток Сила тока, напряжение ,ЭДС, законы и правила
Часть 2 4.4. Зарядка конденсатора - Постоянный электрический ток Сила тока, напряжение
Часть 3 4.5. Правила Кирхгофа - Постоянный электрический ток Сила тока, напряжение
Часть 4 4.7. Классическая теория - Постоянный электрический ток Сила тока, напряжение
либо как отношение заряда к емкости q/C. Приравнивая эти выражения, получаем первое уравнение процесса зарядки
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика