Лекция
Привет, мой друг, тебе интересно узнать все про обозначения в сопромате, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое обозначения в сопромате , настоятельно рекомендую прочитать все из категории Сопротивление материалов.
Сопротивление материалов (в обиходе — сопромат) — часть механики деформируемоготвердого тела, которая рассматривает методы инженерных расчетов конструкций напрочность, жесткость и устойчивость при одновременном удовлетворении требованийнадежности, экономичности и долговечности.
Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нем, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела, называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями, которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейными (удлинение, укорочение, сдвиг) и угловыми (поворот сечений). Основные понятия сопротивления материалов, оценивающие способность материала сопротивляться внешним воздействиям:
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальнойчасти — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета ее прочности, жесткости и надежности.
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций инапряжений в твердом упругом теле, которое подвергается силовому или тепловому воздействию.
Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает ее главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твердых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.
Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:
Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (температуры, распределения напряжений, вида нагрузки и т. п.) большинство материалов может быть отнесено к хрупким, пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень ее приемлемости для механики сплошных сред не всегда достаточен.
Математически теория разрушения выражается в виде различных критериев разрушения, справедливых для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение, это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.
Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
Классические теории прочности имеют существенные ограничения для их применения. Об этом говорит сайт https://intellect.icu . Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причем только для некоторых определенных условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон(Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона.
На смену «классическим» теориям прочности в современной практике пришли многочисленные новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:
Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчета анизотропных материалов.
Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учетом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.
Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.
Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).
В студенческой среде сопротивление материалов считается одной из наиболее сложных общепрофессиональных дисциплин, в основном из-за тяжелой сухой подачи теории, отсутствия хороших наглядных учебных пособий, компьютерного моделирования и учебного видео, что дало богатую пищу студенческому фольклору и породило целый ряд шуток и анекдотов.
| Р - сосредоточенная сила (условно как бы приложенная в одной точке) |
| g - интенсивность распределенной нагрузки, сила на единицу длины (Н/м, МН/м) |
| М - внешний момент, действующий на элемент конструкции (изгибающий или крутящий) |
| у - удельный вес материала |
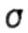 - нормальное напряжение (сигма - нормальное напряжение (сигма 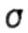 ) ) |
| т - касательное напряжение (тау т) |
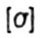 - допускаемое нормальное напряжение - допускаемое нормальное напряжение |
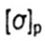 - допускаемое нормальное напряжение при растяжении - допускаемое нормальное напряжение при растяжении |
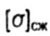 - допускаемое нормальное напряжение при сжатии - допускаемое нормальное напряжение при сжатии |
[т] - допускаемое касательное напряжение [т] = (0,5...0,6) [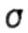 ] ] |
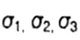 - главные напряжения (экстремальные нормальные) - главные напряжения (экстремальные нормальные) |
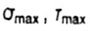 - максимальные напряжения - максимальные напряжения |
 - напряжения по произвольной наклонной площадке - напряжения по произвольной наклонной площадке |
| n, ny - коэффициенты запаса прочности и устойчивости |
| N - продольная сила |
| Qx, Qy - поперечные силы |
| Мx, Мy - изгибающие моменты относительно осей X и У |
| Мp - крутящий момент (относительно продольной оси Z) |
| Е - модуль упругости Юнга для широкого круга материалов (Е = 2-105МПа) |
| G - модуль сдвига (G= 8 • 104 МПа) или G градиент местных напряжений |
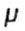 - коэффициент Пуассона - коэффициент Пуассона 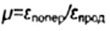 |
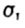 - предел текучести - предел текучести |
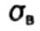 - предел прочности - предел прочности |
 - предел пропорциональности - предел пропорциональности |
 - относительное продольное удлинение (в тексте просто линейное перемещение от единичной силы) - относительное продольное удлинение (в тексте просто линейное перемещение от единичной силы) |
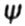 - относительное поперечное сужение - относительное поперечное сужение |
| u - потенциальная энергия деформации |
| А - работа внешней силы |
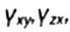 - угловые сдвиговые деформации в разных плоскостях - угловые сдвиговые деформации в разных плоскостях |
 - главные относительные деформации - главные относительные деформации |
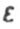 - относительное продольное удлинение (или укорочение) - относительное продольное удлинение (или укорочение) |
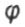 - угол закручивания поперечного сечения вала при кручении или коэффициент снижения основного до пускаемого напряжения - угол закручивания поперечного сечения вала при кручении или коэффициент снижения основного до пускаемого напряжения |
| d - диаметр круглого стержня |
| у - прогиб балки при изгибе |
| Z - координата произвольной точки сечения при рассечении по методу РОЗУ |
| F - площадь поперечного сечения стержней, балок и валов |
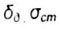 - обобщенные динамические и аст статические перемещения - обобщенные динамические и аст статические перемещения |
| GB - вес груза |
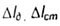 - изменение длины стержня при динамическом и статическом действии силы - изменение длины стержня при динамическом и статическом действии силы |
| U - потенциальная энергия |
| Т - кинетическая энергия |
| dm - масса частицы упругой системы |
| v - скорость |
| Т - температура абсолютной хрупкости |
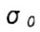 - предел выносливости при отнулевом (пульсирующем) цикле стандартных образцов - предел выносливости при отнулевом (пульсирующем) цикле стандартных образцов |
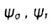 - коэффициенты, характеризующие чувствительность материала к ассиметрии цикла - коэффициенты, характеризующие чувствительность материала к ассиметрии цикла |
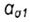 - теоретический коэффициент концентрации напряжений - теоретический коэффициент концентрации напряжений |
 - номинальное значение напряжения в делали без концентратора - номинальное значение напряжения в делали без концентратора |
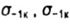 -пределы выносливости образца с концентрацией напряжений -пределы выносливости образца с концентрацией напряжений |
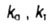 - эффективные коэффициенты концентрации напряжений при изгибе и кручении - эффективные коэффициенты концентрации напряжений при изгибе и кручении |
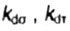 - коэффициенты, учитывающие масштабный фактор детали - коэффициенты, учитывающие масштабный фактор детали |
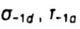 - предел выносливости гладких образцов диаметром d - предел выносливости гладких образцов диаметром d |
| G - градиент местных напряжений |
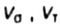 - коэффициенты чувствительности металла к концентрации напряжений и масштабному фактору - коэффициенты чувствительности металла к концентрации напряжений и масштабному фактору |
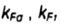 - коэффициенты, учитывающие влияние на пределы выносливости детали качества обработки поверхности - коэффициенты, учитывающие влияние на пределы выносливости детали качества обработки поверхности |
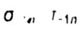 - пределы выносливости образца с заданным качеством поверхности - пределы выносливости образца с заданным качеством поверхности |
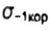 - предел выносливости образца в коррозионной среде - предел выносливости образца в коррозионной среде |
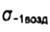 - предел выносливости образца на воздухе - предел выносливости образца на воздухе |
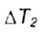 - сдвиг критической температуры от степени концентрации напряжений - сдвиг критической температуры от степени концентрации напряжений |
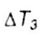 - сдвиг критической температуры от увеличения размеров трещин - сдвиг критической температуры от увеличения размеров трещин |
 - сдвиг критической температуры от многократного циклического по вреждения - сдвиг критической температуры от многократного циклического по вреждения |
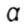 - коэффициент концентрации напряжений - коэффициент концентрации напряжений |
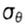 - окружное напряжение в окрестностях трещины - окружное напряжение в окрестностях трещины |
 - единичный коэффициент канонического уравнения метода сил - единичный коэффициент канонического уравнения метода сил |
 - грузовой член канонического уравнения метода сил - грузовой член канонического уравнения метода сил |
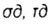 - нормальные и касательные динамические напряжения - нормальные и касательные динамические напряжения |
 - предел выносливости упрочненного образца - предел выносливости упрочненного образца |
 - коэффициенты снижения предела выносливости детали, соответственно при изгибе и кручении - коэффициенты снижения предела выносливости детали, соответственно при изгибе и кручении |
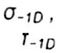 - пределы выносливости детали - пределы выносливости детали |
 - коэффициенты запаса прочности соответственно по нормальным касательным напряжениям - коэффициенты запаса прочности соответственно по нормальным касательным напряжениям |
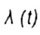 - интенсивность отказов - интенсивность отказов |
 - число изделий, отказавших за время t - число изделий, отказавших за время t |
 - функция неразрушимости - функция неразрушимости |
Тебе нравиться обозначения в сопромате? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое обозначения в сопромате и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов
Комментарии
Оставить комментарий
Сопротивление материалов
Термины: Сопротивление материалов