ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ кратко

Лекция

Привет, мой друг, тебе интересно узнать все про перемещения при изгибе, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое перемещения при изгибе , настоятельно рекомендую прочитать все из категории Сопротивление материалов.

Пример 1.

Для балки, защемленной одним концом и нагруженной на свободном конце силой Р, определить прогибы свободного конца (рис. 6.4) и сечения к (рис. 6.5).

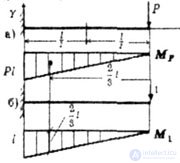ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ

Рис. 6.4

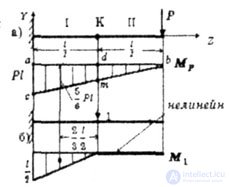Рис. 6.5

Решение.

Определим прогиб свободного конца.

Строим эпюру изгибающих моментов М_p от заданной силы Р (рис. 6.4,а).
Освобождаем балку от силы Р и затем по направлению искомого прогиба на свободном конце прикладываем единичную силу и строим от нее единичную эпюру изгибающих моментов М₁ (рис. 6.4,б).
Вычисляем прогиб свободного конца по формуле (2). Для этого перемножаем по способу Верещагина эпюры М_p и М₁ .

Так как обе эпюры линейны, безразлично на какой из них брать площадь и на какой ординату.
Обе эпюры лежат по одну сторону оси, поэтому их перемножение дает плюс.

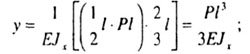Теперь определим прогиб сечения К. Эпюра изгибающего момента от силы Р (рис. 6.5,а) останется та же самая и будет линейна на всем протяжении балки, а эпюра от единичной силы, приложенной в сечении К (рис. 6.5,б) - ломаная, поэтому, применяя правило Верещагина, берем площадь эпюры М₁, а ординату на эпюре М_p.

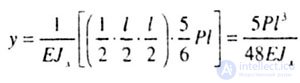Пример 2.

Определить угол поворота точки С балки, защемленной левым концом и нагруженной равномерно распределенной нагрузкой q (рис. 6.6).

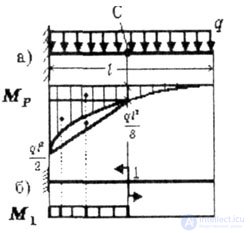Рис. Об этом говорит сайт https://intellect.icu . 6.6

Решение.

Строим эпюру изгибающих моментов М_p (рис. 6.6,а) от заданной распределенной нагрузки q.
Освобождаем балку от распределенной нагрузки q и затем по направлению искомого угла поворота сечения С прикладываем единичный момент и строим от него эпюру единичных моментов М₁ (Рис. 6 6.6).
Определяем угол поворота сечения С перемножая эпюры М_p и М₁ Эпюра М_p сравнительно сложна, во всяком случае, непосредственное определение площади и координат центра тяжести без вспомогательных расчетов невозможно. Для того, чтобы их избежать, разбиваем эпюры М на такие части, для которых имеются готовые формулы площадей и координат центров тяжести. На эпюре (рис. 6.6,б) показана рекомендуемая разбивка на отдельные части: прямоугольник, треугольник и параболический сегмент. Площади и расположение центров тяжести этих фигур приведены выше, а поэтому дальнейшее решение задачи не представляет затруднения:

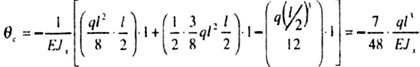Пример 3.

Для заданной балки со сплошной равномерно распределенной нагрузкой интенсивностью q определить прогиб в сечении С. (рис. 6.7).

Во многих случаях оказывается удобным строить грузовую эпюру в так называемом "расслоенном" виде: строят ряд самостоятельных эпюр от каждой нагрузки. Сущность расслоения эпюр покажем на конкретном примере (рис. 6.7.).

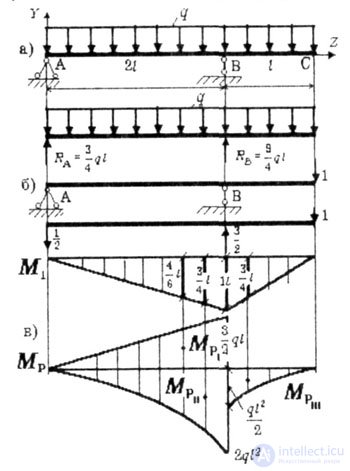Рис. 6.7

Решение.

1. Если при построении эпюр изгибающих моментов в консольных балках определение реакций было необязательно, то для двух-опорных балок невозможно построить эпюры, не определив предварительно реакции. Определяем реакции опор (рис. 6.7,а)

2. Сняв заданную нагрузку, прикладываем в сечении С единичную сосредоточенную силу и от этой единичной силы определяем реакции опор

и строим эпюру М₁ (рис. 6.7,б). Единичная эпюра имеет излом в т.В. Поэтому расслоение грузовой эпюры удобно провести по отношению к сечению В, подходя к нему с двух сторон (рис. 6.7,в). Слева строим эпюры от реакции R_A, распределенной нагрузки q; справа - от распределенной нагрузки q.

3. Определяем прогиб в сечении С.

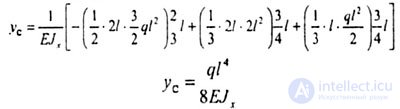Можно рекомендовать еще один прием перемножения эпюр.

Умножать эпюры, имеющие вид трапеций, "перекрученных" трапеций или когда одна из эпюр очерчена по квадратной параболе, можно по готовым формулам. При этом нет надобности находить положение центра тяжести площади одной из них (рис. 6.8).

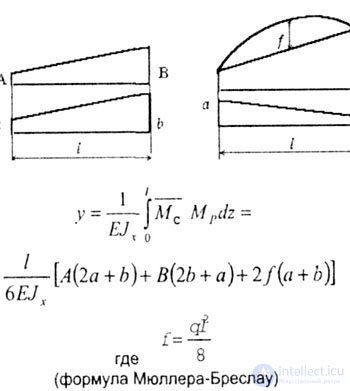Рис. 6.8

Если перемножаются две прямолинейные эпюры (две трапеции), то в последней формуле сохраняются только два слагаемых.

Этот метод хорош для машинного счета.

Примечание.

Последняя формула применима и тогда, когда одна или обе перемножаемые эпюры имеют вид треугольника. В этих случаях треугольник рассматривается как трапеция с одной крайней ординатой, равной нулю.

Пример 4.

Определить угол поворота сечения К балки (рис. 6.9).

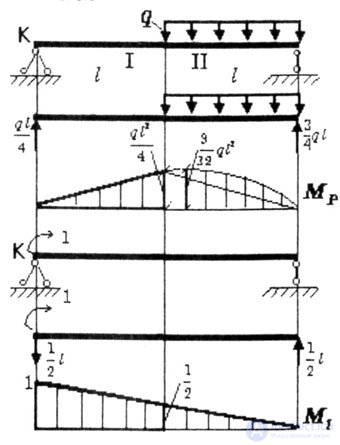Рис. 6.9

параболического треугольника с высотой.

Решение:

1-ый способ.

Как и в предыдущих задачах строим эпюру М_p и М₁. Эпюра М_p состоит из равнобедренного треугольника с высотой

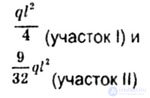Воспользуемся формулой Мюллера-Бреслау

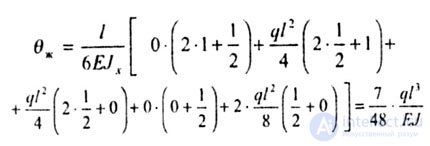2-ой способ.

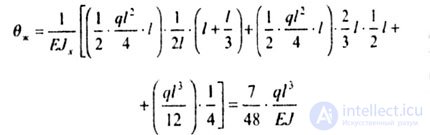Ответы совпали.

Тебе нравиться перемещения при изгибе? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое перемещения при изгибе и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов

Из статьи мы узнали кратко, но содержательно про перемещения при изгибе

ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ кратко

Комментарии

Оставить комментарий

Сопротивление материалов

Термины: Сопротивление материалов