Лекция
Привет, мой друг, тебе интересно узнать все про определение критической силы с помощью дифференциального уравнения, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое определение критической силы с помощью дифференциального уравнения , настоятельно рекомендую прочитать все из категории Сопротивление материалов.
| определение критической силы с помощью дифференциального уравнения (ТОЧНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ Ркр). |
| Если коэффициент приведения длины не очевиден, то Ркр можно найти, решая дифференциальное уравнение - это точный метод определения критической силы. |
| Особенностью задач устойчивости является тот факт, что рассматривается равновесие стержня в деформированном состоянии, в то время как в других разделах составляются уравнения равновесия для элемента нагруженного стержня (или иного тела) без участка его изменений вследствие деформаций. |
| Общий порядок расчета: |
|
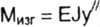 |
получим дифференциальные уравнения равновесия в количестве, равном числу участков (при этом обозначим 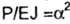 ); ); |
| Используя граничные условия на концах стержня и условия стыковки участков (равенство перемещений и углов поворота в конце предыдущего и в начале последующего участка, так как изогнутая ось стержня - плавная кривая без изломов и разрывов), получаем так называемое характеристическое уравнение. |
Решая полученное (чаще всего трансцендентное) уравнение подбором, графически или с помощью ЭВМ, получаем ряд значений 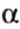 , удовлетворяющих уравнению и граничным условиям задачи. Об этом говорит сайт https://intellect.icu . Наименьшее (отличное от нуля) из полученных значений , удовлетворяющих уравнению и граничным условиям задачи. Об этом говорит сайт https://intellect.icu . Наименьшее (отличное от нуля) из полученных значений 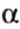 дает выражение для критической силы в виде дает выражение для критической силы в виде |
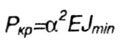 |
Тебе нравиться определение критической силы с помощью дифференциального уравнения? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое определение критической силы с помощью дифференциального уравнения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов
Из статьи мы узнали кратко, но содержательно про определение критической силы с помощью дифференциального уравнения
Комментарии
Оставить комментарий
Сопротивление материалов
Термины: Сопротивление материалов