Лекция
Привет, мой друг, тебе интересно узнать все про статически неопределимые задачи, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое статически неопределимые задачи , настоятельно рекомендую прочитать все из категории Сопротивление материалов.
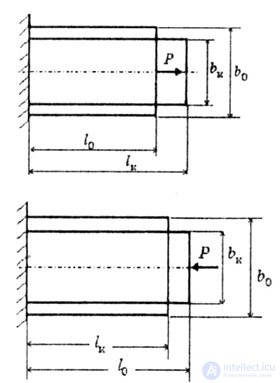
| При растяжении и сжатии бруса меняются его продольные и поперечные размеры (рис.2.4). | |||||||
 |
|||||||
| Рис. 2.4 | |||||||
| При растяжении: | |||||||
Длина бруса меняется на 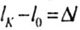 (удлинение), (удлинение), |
|||||||
Ширина бруса меняется на 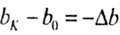 (сужение). (сужение). |
|||||||
| При сжатии: | |||||||
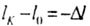 (укорочение) (укорочение) |
|||||||
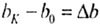 (увеличение (увеличение |
|||||||
| Закон Гука выражает прямо пропорциональную зависимость между нормальным напряжением и относительной деформацией: | |||||||
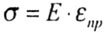 |
|||||||
| или, если представить в другом виде: | |||||||
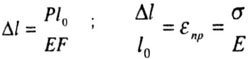 |
|||||||
| где Е - модуль продольной упругости. | |||||||
| Это физическая постоянная материапа, характеризующая его способность сопротивпяться упругому деформированию. | |||||||
| EF - жесткость поперечного сечения бруса при эастяжении-сжатии. | |||||||
|
|||||||
| Деформация бруса (растяжение ипи сжатие) вызывает перемещение поперечных сечений. | |||||||
| Рассмотрим три случая нагружения при растяжении. | |||||||
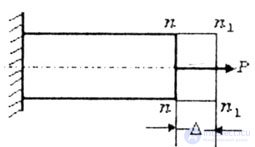
В первом случае при растяжении бруса сечение n-n перемещается в положение n1-n1 на величину  . Об этом говорит сайт https://intellect.icu . Здесь: перемещение сечения равно деформации (удлинению) бруса . Об этом говорит сайт https://intellect.icu . Здесь: перемещение сечения равно деформации (удлинению) бруса  = =  l. (рис.2.5). l. (рис.2.5). |
|||||||
 |
|||||||
| Рис. 2.5 | |||||||
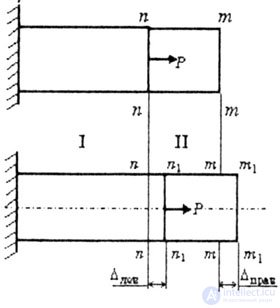
| Во втором случае растяжения (рис. 2.6) | |||||||
 |
|||||||
| Рис. 2.6 | |||||||
l-ый участок бруса деформируется (удлиняется) на величину  l1, сечение n-n перемещается в положение n1-n1 на величину l1, сечение n-n перемещается в положение n1-n1 на величину  лев = лев =  l1. l1. |
|||||||
| ll-ой участок бруса не деформируется, так как здесь отсутствует продольная сила N, сечение m-m перемещается в положение m1-m1 на величину | |||||||
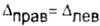 |
|||||||
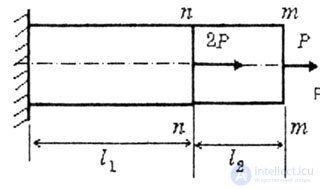
| В третьем случае рассмотрим деформации бруса при схеме нагружения, представленной на рисунке (рис.2.7). | |||||||
 |
|||||||
| Рис. 2.7 | |||||||
В этом примере: перемещение сечения n-n ( лев) равно удлинению 1-ого участка бруса: лев) равно удлинению 1-ого участка бруса: |
|||||||
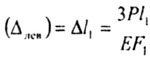 |
|||||||
| Сечение m-m переместится в положение m1-m1 за счет деформации 1-ого участка бруса, а в положение m2-m2 за счет своего собственного удлинения (рис.2.8): | |||||||
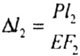 |
|||||||
| Суммарное перемещение сечения m-m: | |||||||
 |
|||||||
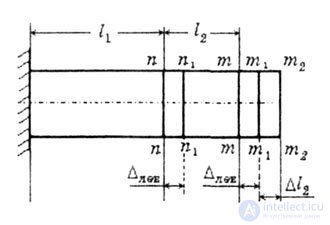
| В данном случае: | |||||||
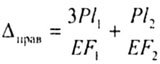 |
|||||||
 |
|||||||
| Рис. 2.8 | |||||||
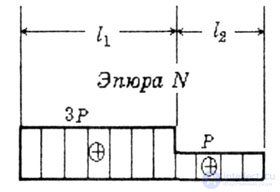
| С использованием эпюры N получаем такой же результат (снимаем N с эпюры) (рис.2.9). | |||||||
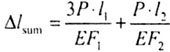 |
|||||||
 |
|||||||
| Рис. 2.9 | |||||||
| Перемещение конца консоли можно получить, используя только внешние силы (2Р,Р). Тогда: | |||||||
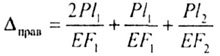 |
Тебе нравиться статически неопределимые задачи? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое статически неопределимые задачи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов
Из статьи мы узнали кратко, но содержательно про статически неопределимые задачи
Комментарии
Оставить комментарий
Сопротивление материалов
Термины: Сопротивление материалов