Лекция
Привет, Вы узнаете о том , что такое плоское напряженное состояние, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое плоское напряженное состояние, напряженное состояние , настоятельно рекомендую прочитать все из категории Сопротивление материалов.
Наиболее часто в задачах сопротивления материалов встречается плоское напряженное состояние : при кручении, изгибе, изгибе с кручением и т.д. Остановимся на нем подробнее.
Выделим из тела параллелепипед (Рис.9.8). Под действием сил, приложенных к его граням, параллелепипед находится в равновесии. Длины ребер параллелепипеда считаем бесконечно малыми и равными 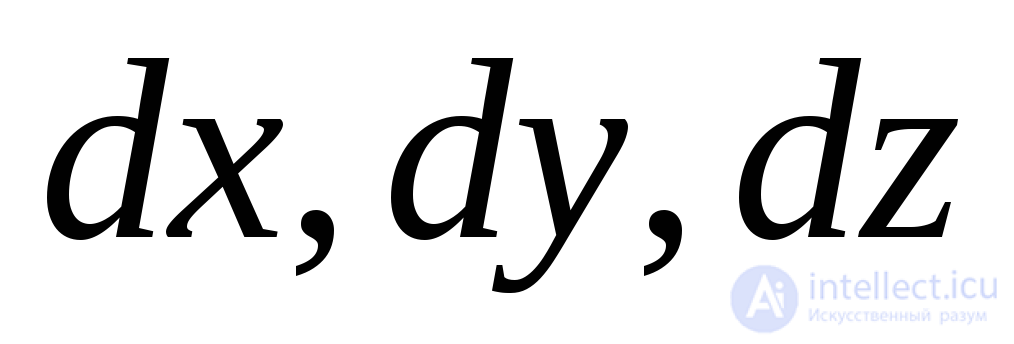 .
.

Рис.9.8
Рассмотрим наклонные площадки, перпендикулярные незагруженным граням параллелепипеда. Разрежем элементарный параллелепипед, изображенный на рис.9.8 , наклонным сечением, перпендикулярным плоскости  , выделив из него элементарную треугольную призму (Рис.9.9а).
, выделив из него элементарную треугольную призму (Рис.9.9а).
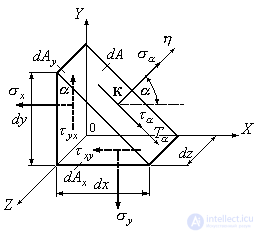
Рис.9.9
Наклон площадки с искомыми напряжениями будем определять углом  , который образует внешняя нормаль к этой площадке с осью
, который образует внешняя нормаль к этой площадке с осью . Из рис.9.9 следует, что
. Из рис.9.9 следует, что
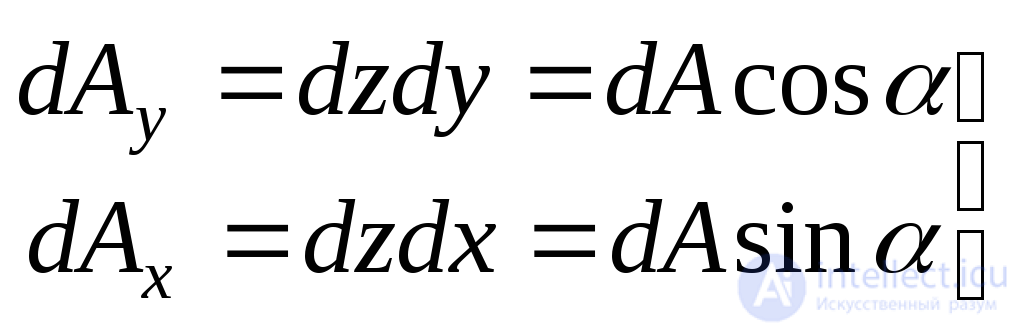
 (9.6)
(9.6)
Система сил, приведенная на рис.9.9, является плоской произвольной системой. Равновесие такой системы сил описывается тремя независимыми уравнениями. Составим эти уравнения.
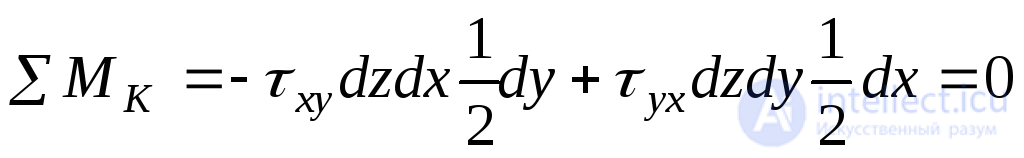 . (9.7)
. (9.7)
Откуда:
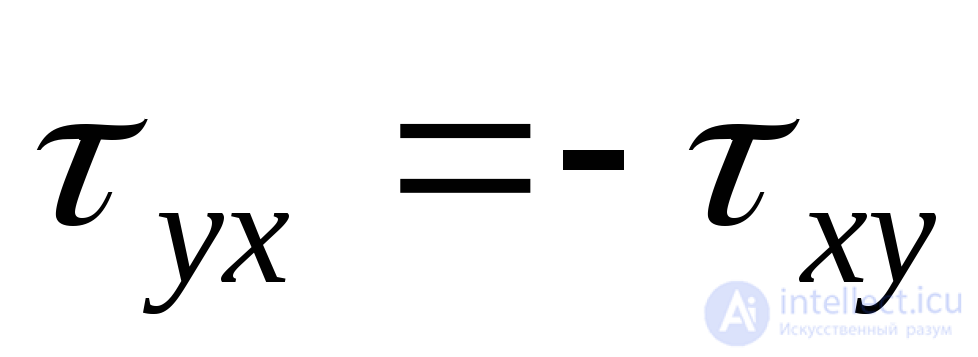 . (9.8)
. (9.8)
Выражение (9.8) представляет собой закон парности касательных напряжений: касательные напряжения, действующие на двух любых взаимно перпендикулярных площадках, равны по величине и противоположны по знаку.
При плоском напряженном состоянии возможны лишь два варианта действия касательных напряжений (Рис.9.10).

Рис.9.10
Для определения напряжений на наклонной площадке спроектируем силы, действующие на призму (Рис.9.9) на оси  и
и . Получим:
. Получим:
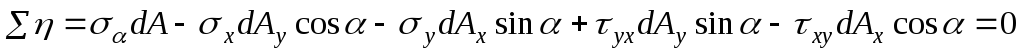 ; (9.9)
; (9.9)
 . (9.10)
. (9.10)
Подставляя в (9.9)-(9.10) вместо 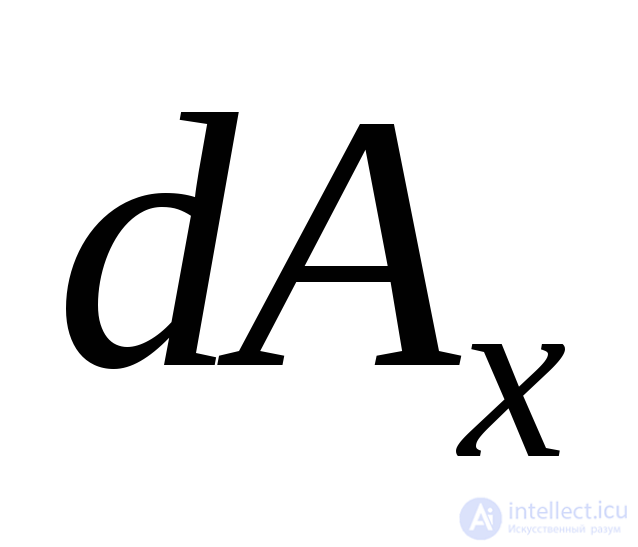 и
и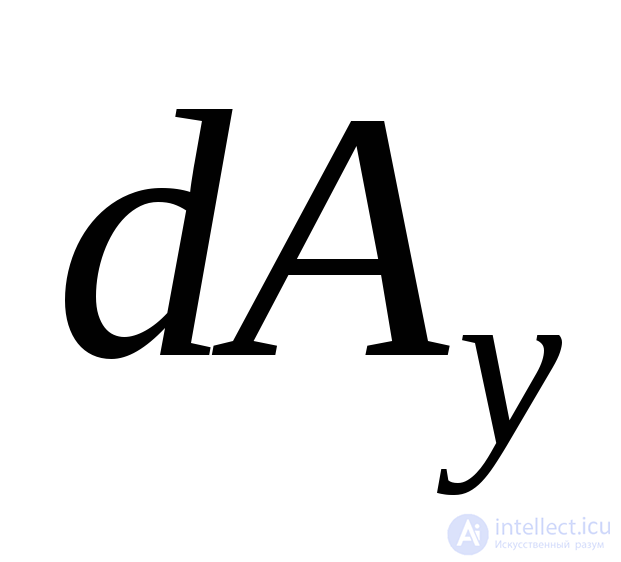 из выражения (9.6), сократим все слагаемые на
из выражения (9.6), сократим все слагаемые на . Далее, учитывая, что согласно (9.8)
. Далее, учитывая, что согласно (9.8)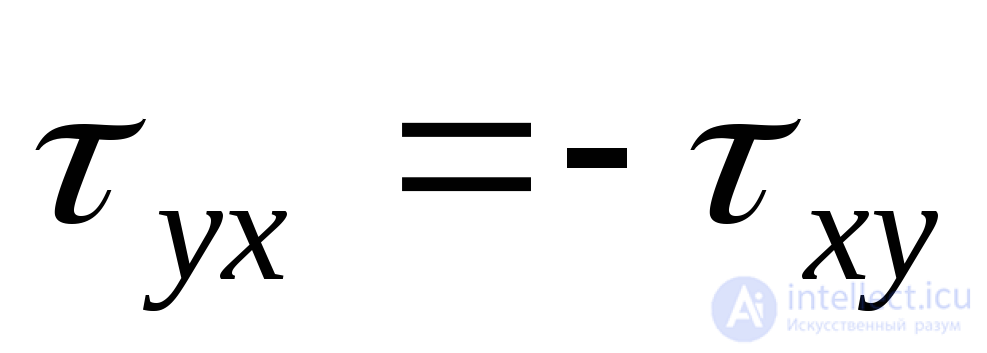 , а
, а и
и , находим:
, находим:
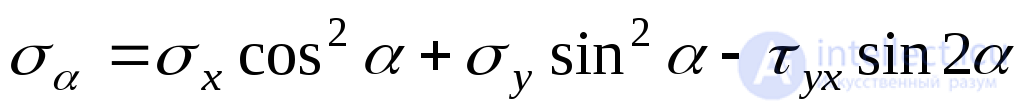 ; (9.11)
; (9.11)
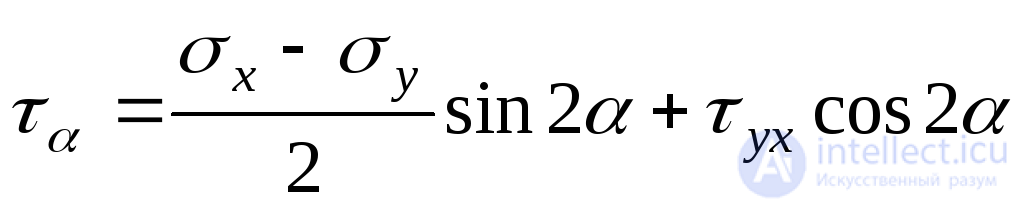 . (9.12)
. (9.12)
Представим формулу (9.9) в несколько ином виде, используя известные из тригонометрии равенства:
 . (9.13)
. (9.13)
Подставляя (9.13) в (9.11), получаем:
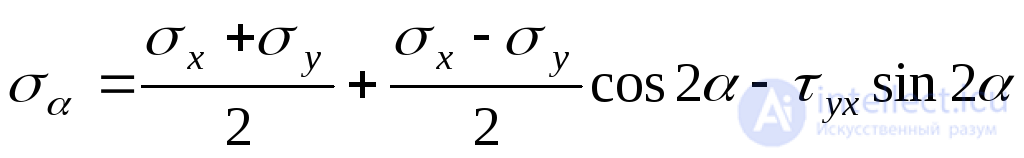 . (9.14)
. (9.14)
Выясним связь между нормальными напряжениями  и
и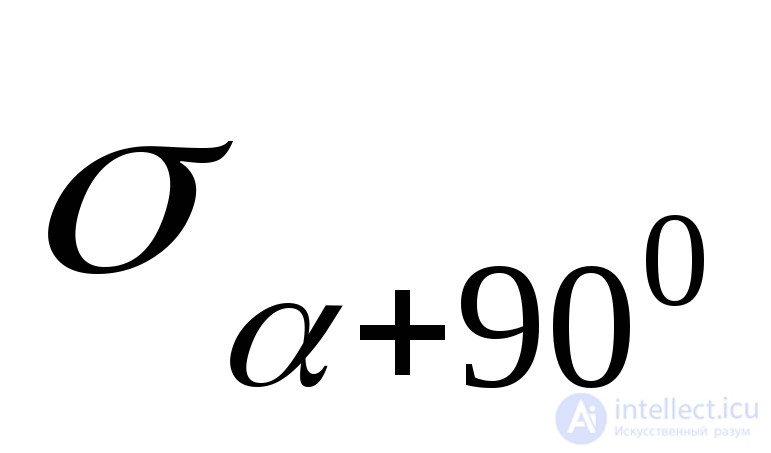 , действующими на двух взаимно перпендикулярных площадках (Рис.9.11).
, действующими на двух взаимно перпендикулярных площадках (Рис.9.11).

Рис.9.11
Напряжение  определяется по формуле (9.14). Напряжение
определяется по формуле (9.14). Напряжение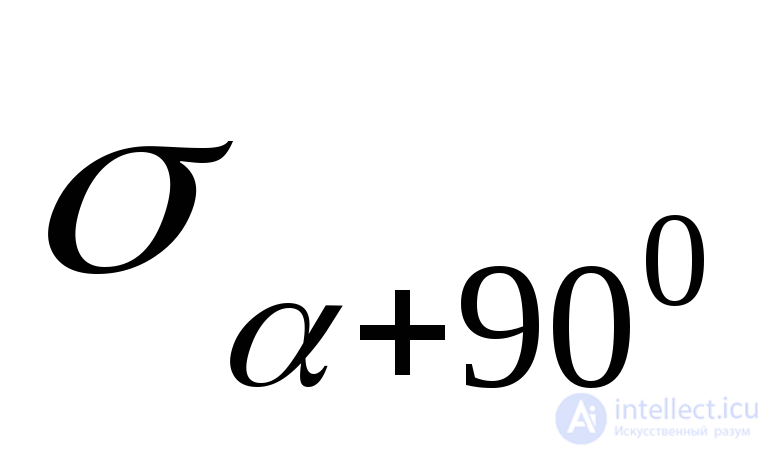 получим, если в эту формулу подставим
получим, если в эту формулу подставим :
:
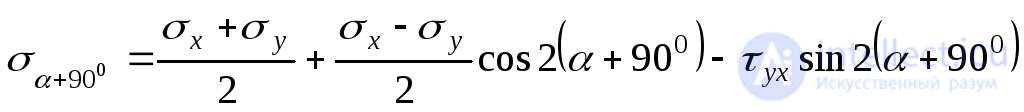
или
 . (9.15)
. (9.15)
Складывая (9.14) и (9.15), приходим к выводу:
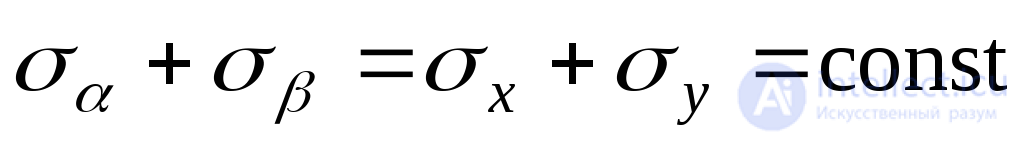 . (9.16)
. (9.16)
Выражение (9.16) получило названия условия инвариантности суммы нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам: в данной точке алгебраическая сумма нормальных напряжений, действующих по любым двум взаимно перпендикулярным площадкам, есть величина постоянная. Это условие используют для проверки правильности решения задач при исследовании напряженного состояния в точке.
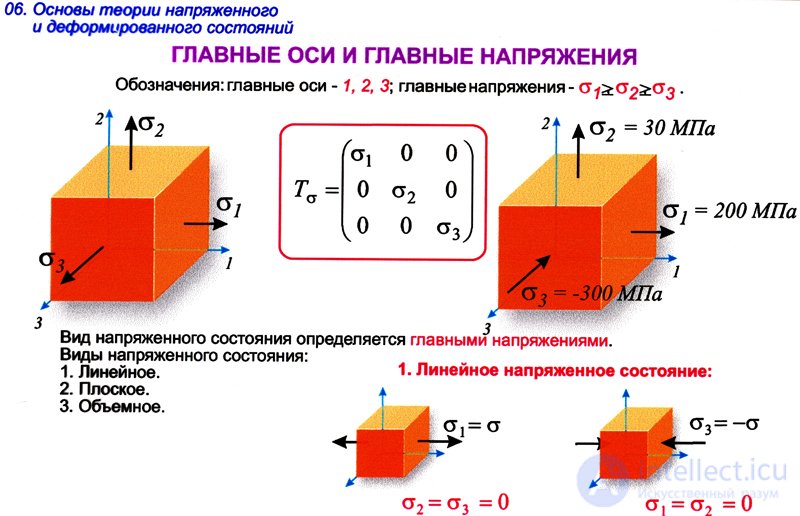
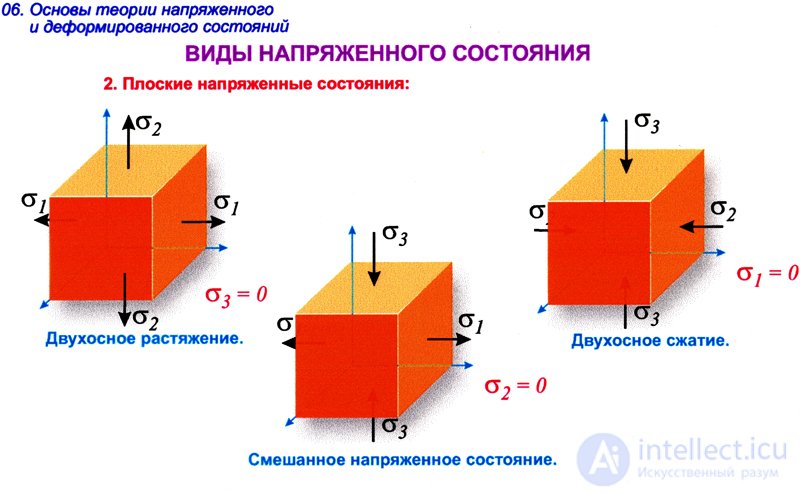
Виды напряженного состояния
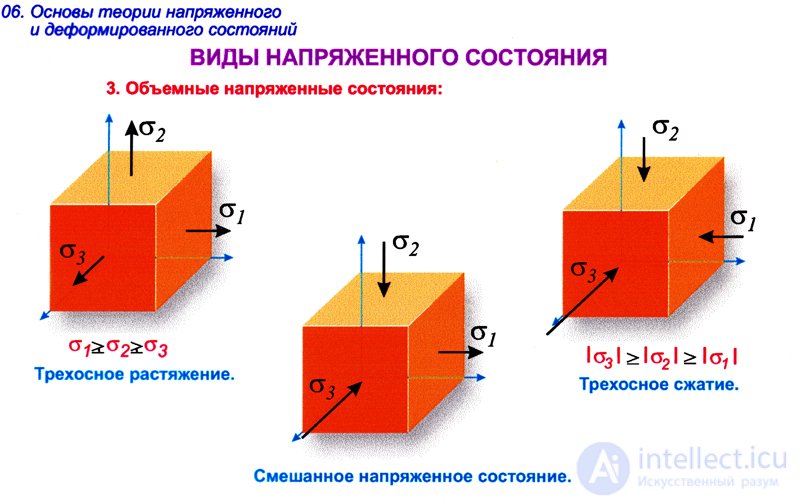
Исследуем выражение для нормальных напряжений (9.14) на экстремум. Для этого возьмем частную производную от напряжения  по
по и приравняем к нулю:
и приравняем к нулю:
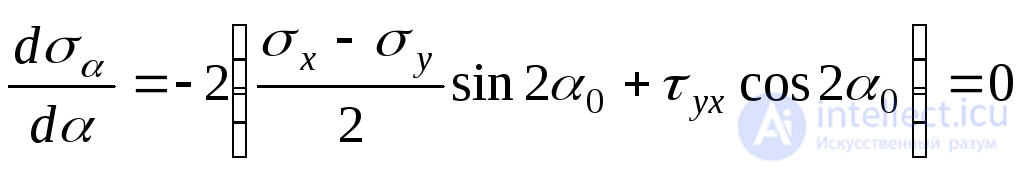 , (9.17)
, (9.17)
где  угол, который составляет нормаль к рассматриваемой площадке с положительным направлением оси
угол, который составляет нормаль к рассматриваемой площадке с положительным направлением оси и при котором нормальное напряжение
и при котором нормальное напряжение достигает наибольшего значения для данной точки .
достигает наибольшего значения для данной точки .
Выражение (9.17) представляет собой величину касательного напряжения в главной площадке 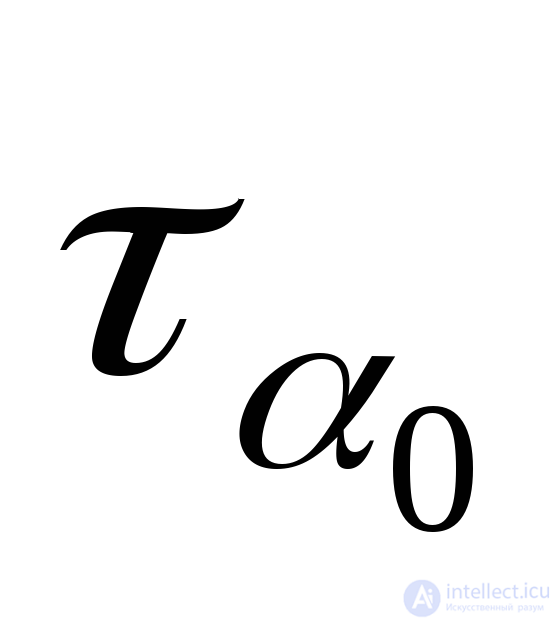 . Таким образом, касательное напряжение в рассматриваемой площадке (
. Таким образом, касательное напряжение в рассматриваемой площадке (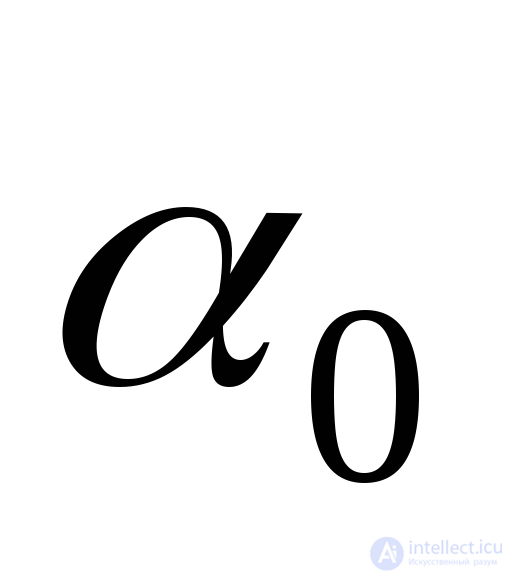 ) равно нулю. Отсюда делаем вывод: площадка, нормаль к которой составляет угол
) равно нулю. Отсюда делаем вывод: площадка, нормаль к которой составляет угол с положительным направлением оси
с положительным направлением оси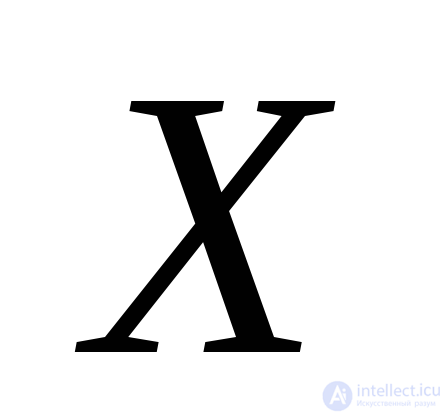 , является главной площадкой.
, является главной площадкой.
Приравнивая выражение в скобках формулы (9.17) нулю найдем тангенс двойного угла, определяющего наклон главных площадок:
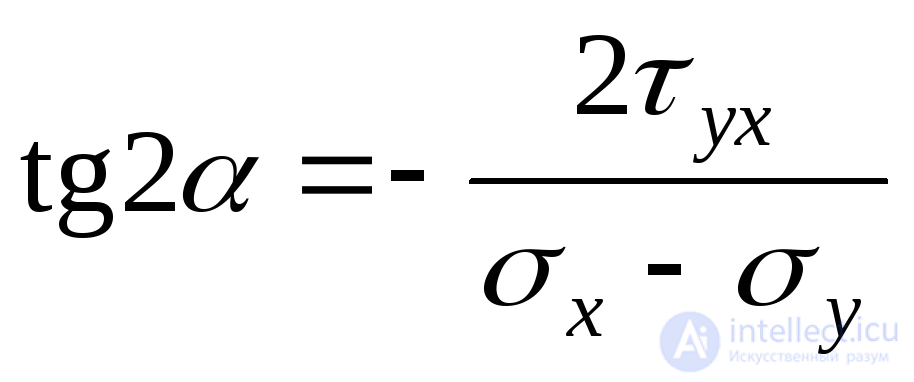 . (9.18)
. (9.18)
Выражение (9.18) дает два взаимно-перпендикулярных направления с углами наклона 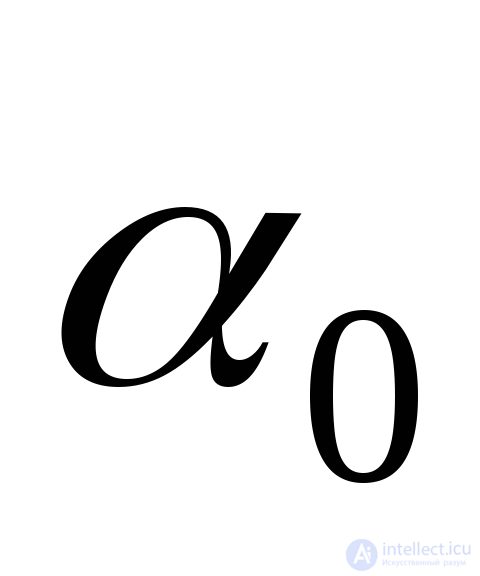 и
и , по которым действуют главные напряжения (Рис.9.12).
, по которым действуют главные напряжения (Рис.9.12).
Для определения величин главных напряжений подставим формулу (9.14)  . Об этом говорит сайт https://intellect.icu . Вынося
. Об этом говорит сайт https://intellect.icu . Вынося за скобку, получим:
за скобку, получим:
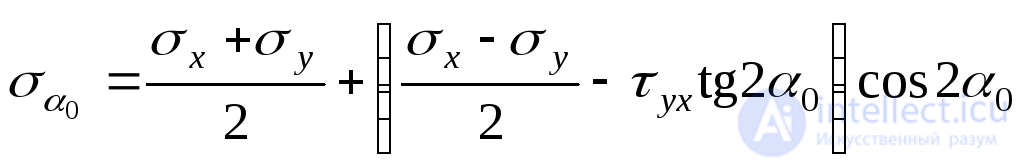 . (а)
. (а)
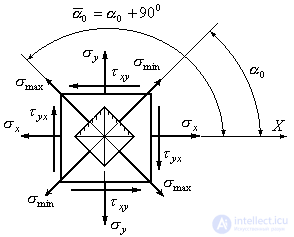
Рис.9.12
Из тригонометрии известно:
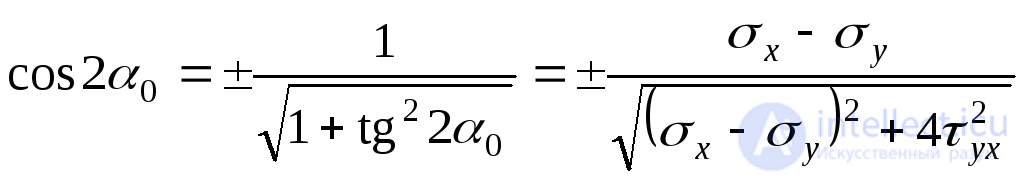 . (б)
. (б)
Знак  поставлен потому, что косинусы углов
поставлен потому, что косинусы углов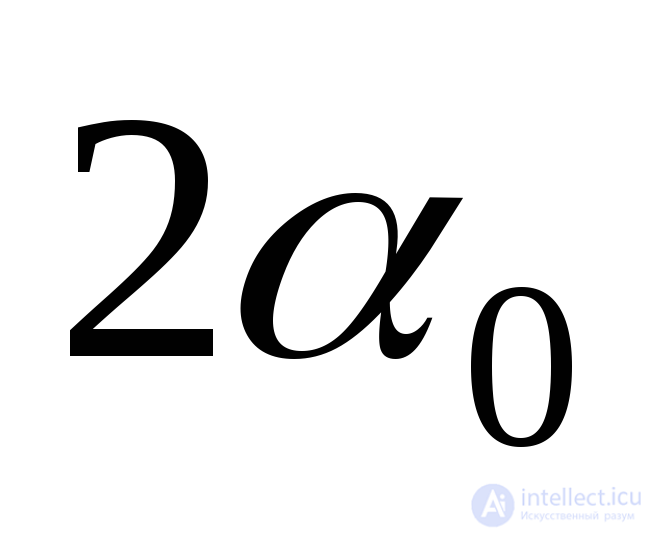 и
и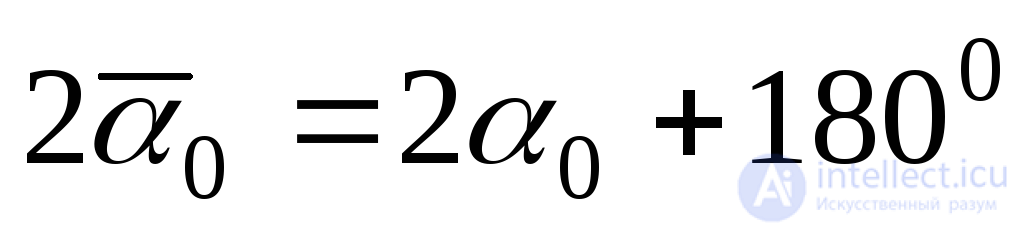 имеют противоположные знаки. Подставляя (9.18) в (б) и (а), получим:
имеют противоположные знаки. Подставляя (9.18) в (б) и (а), получим:
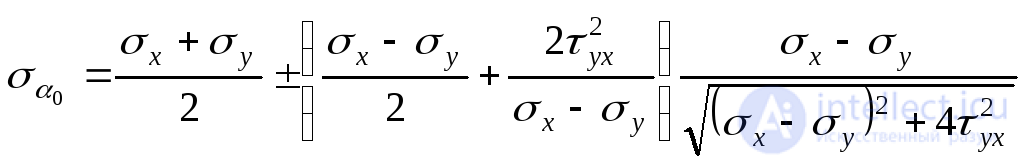
 .
.
В этой формуле знак “плюс”соответствует максимальному главному напряжению , а“минус”минимальному
, а“минус”минимальному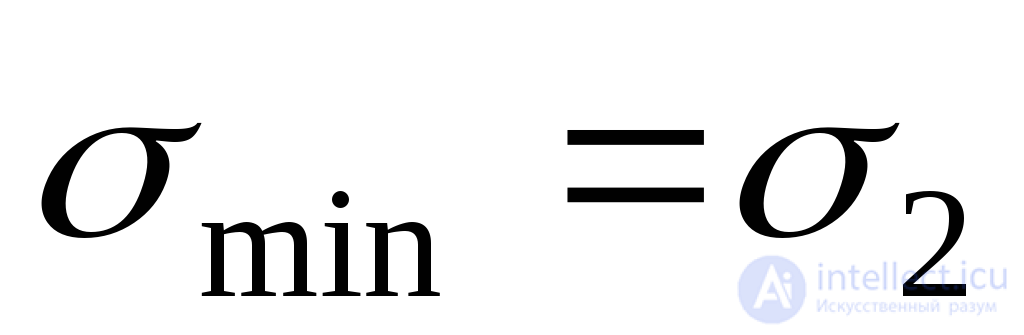 . Таким образом, окончательно имеем:
. Таким образом, окончательно имеем:
 .(9.19)
.(9.19)
Из приведенного вывода следует, что при любых исходных напряжениях  в данной точке существует параллелепипед, на гранях которого действуют только нормальные напряжения.
в данной точке существует параллелепипед, на гранях которого действуют только нормальные напряжения.
Вернемся к формуле (9.18). Она дает два главных направления, но не указывает, в каком из них действует 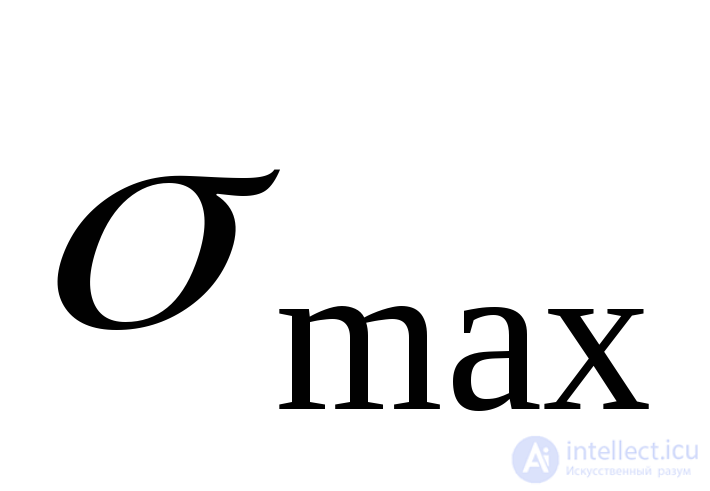 , а в каком
, а в каком . Для решения этого вопроса надо было бы исследовать знак второй производной
. Для решения этого вопроса надо было бы исследовать знак второй производной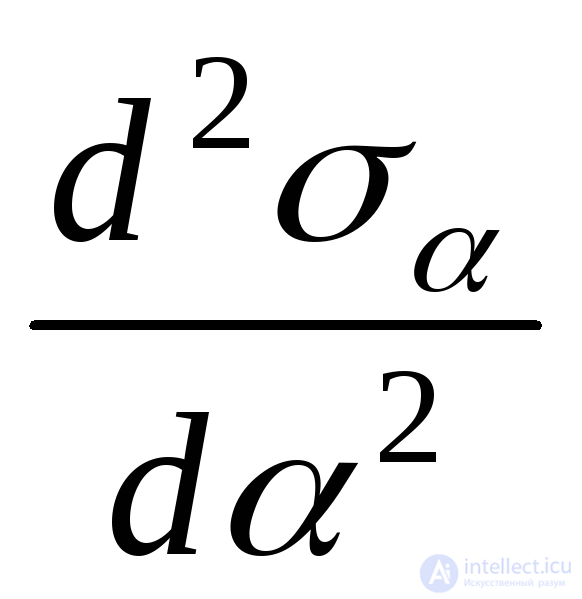 при
при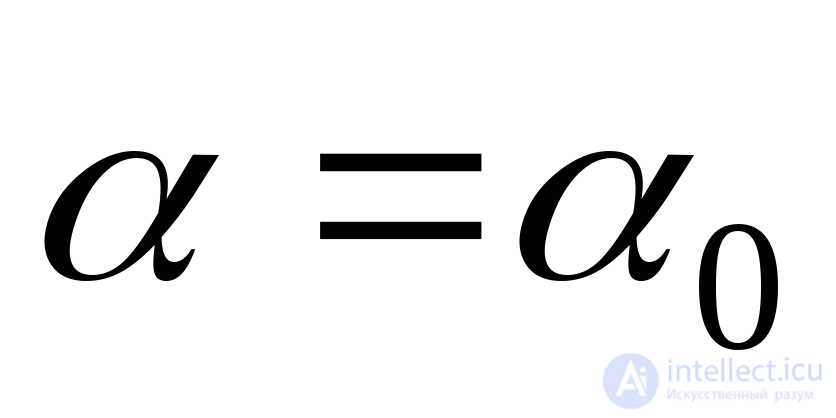 и
и . Однако, можно решить эту задачу, используя выражения, аналогичные тем, которые применялись для определения направления главных осей инерции в разделе“Геометрические характеристики плоских фигур”:
. Однако, можно решить эту задачу, используя выражения, аналогичные тем, которые применялись для определения направления главных осей инерции в разделе“Геометрические характеристики плоских фигур”:
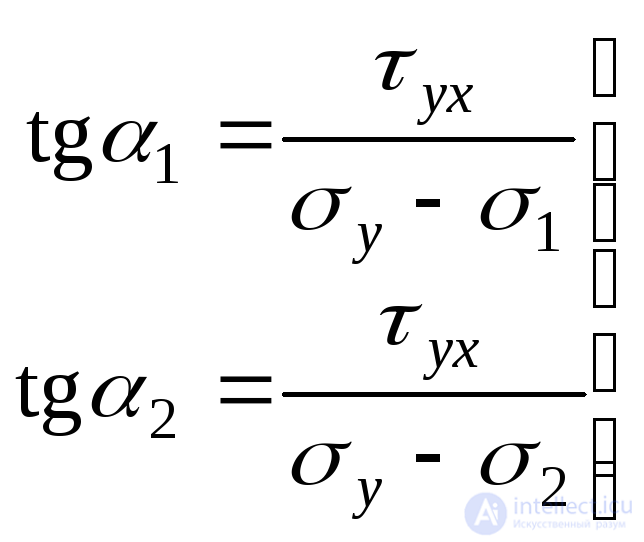 . (9.20)
. (9.20)
Здесь:  угол, который следует отложить от положительного направления оси
угол, который следует отложить от положительного направления оси до нормали к площадки, в которой действует максимальное напряжение
до нормали к площадки, в которой действует максимальное напряжение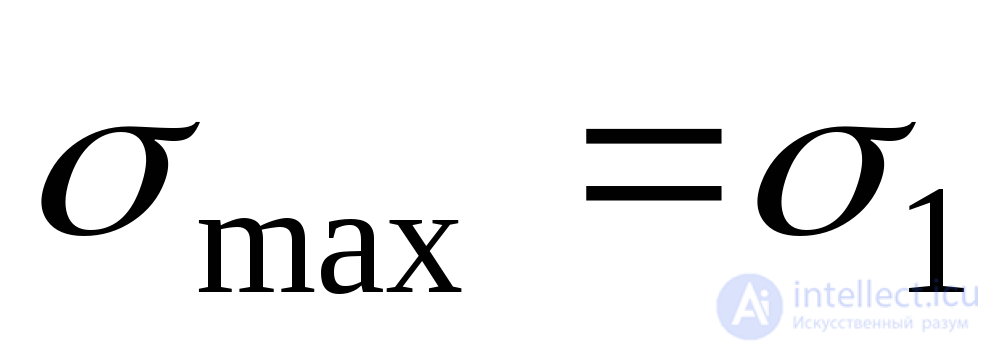 ;
;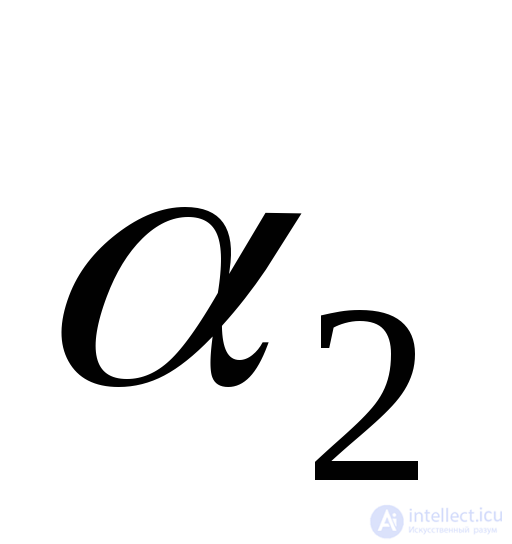 угол, который следует отложить от положительного направления оси
угол, который следует отложить от положительного направления оси до нормали к площадки, в которой действует минимальное напряжение
до нормали к площадки, в которой действует минимальное напряжение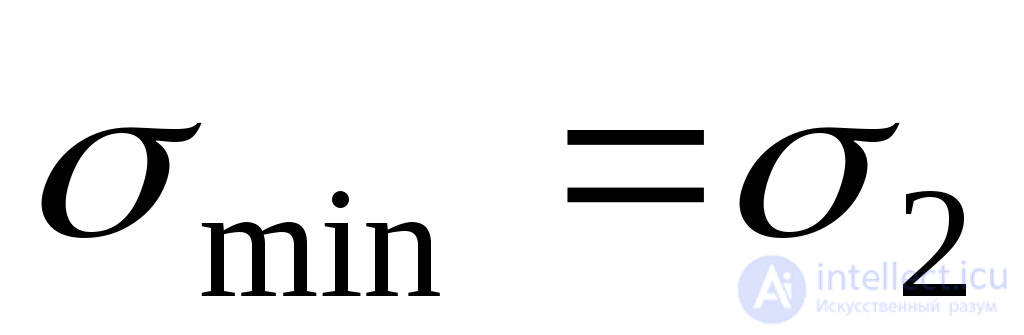 . Положительный угол следует откладывать против хода часовой стрелки, отрицательный – по ходу часовой стрелки.
. Положительный угол следует откладывать против хода часовой стрелки, отрицательный – по ходу часовой стрелки.
Для контроля правильности определения положения главных площадок можно использовать еще один способ, приведенный в . Исходя из того, что с поворотом площадки в направлении вектора касательных напряжений нормальное напряжение на площадке алгебраически возрастает, в работе формулируется следующее правило:направление 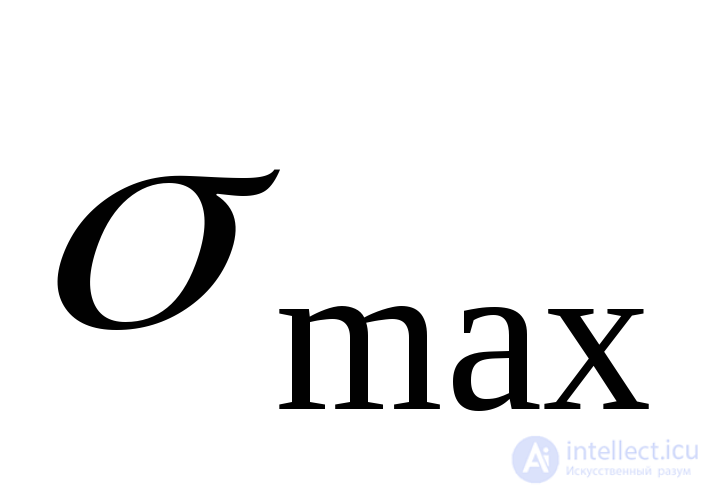 всегда проходит через две четверти осей координат, в которых стрелки касательных напряжений
всегда проходит через две четверти осей координат, в которых стрелки касательных напряжений и
и сходятся.
сходятся.
Примем в качестве исходных площадки, в которых действуют главные напряжения (Рис.9.13).
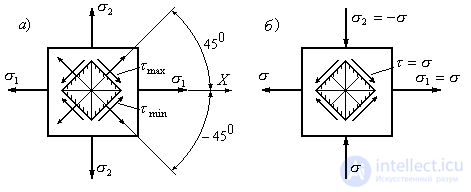
Рис.9.13
Отсчитывая угол  от направления
от направления , напишем выражения для
, напишем выражения для и
и , используя формулы (9.12), (9.14), полагая в них
, используя формулы (9.12), (9.14), полагая в них ,
, , а
, а :
:
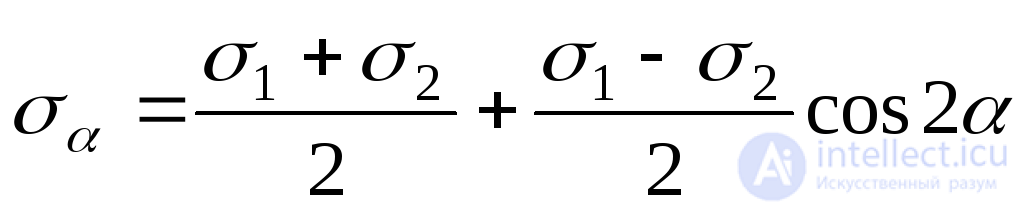 ; (9.21)
; (9.21)
 . (9.22)
. (9.22)
Из формулы (9.22) следует, что при 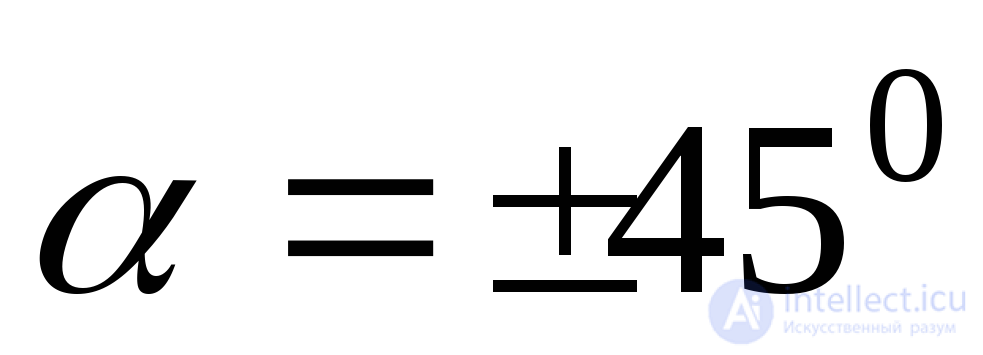 синус двойного угла
синус двойного угла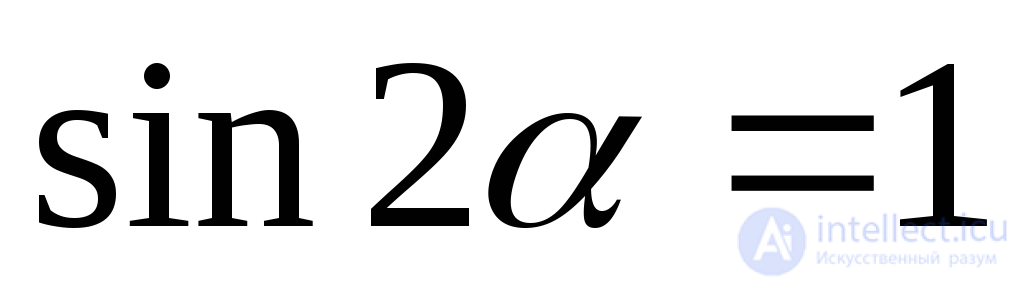 , касательные напряжения имеют экстремальные значения:
, касательные напряжения имеют экстремальные значения:
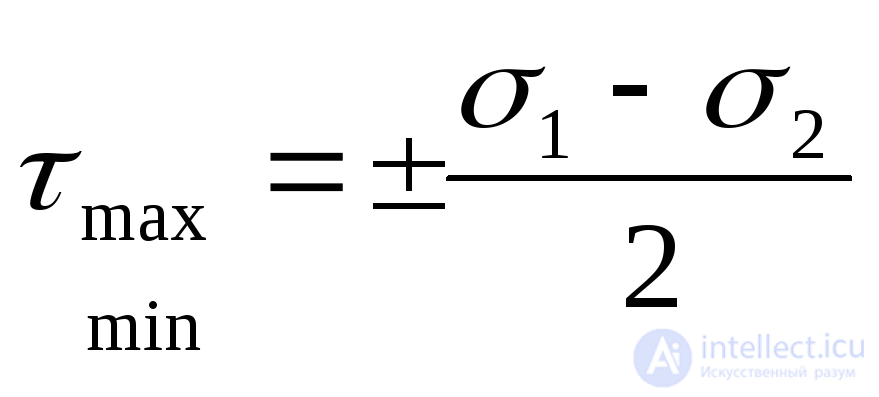 . (9.23)
. (9.23)
Экстремальные касательные напряжения в точке равны полуразности главных напряжений и действуют на площадках, наклоненных к главным площадкам под углом 450(Рис.9.13,а).
Подставляя (9.19) в (9.23), получим выражение 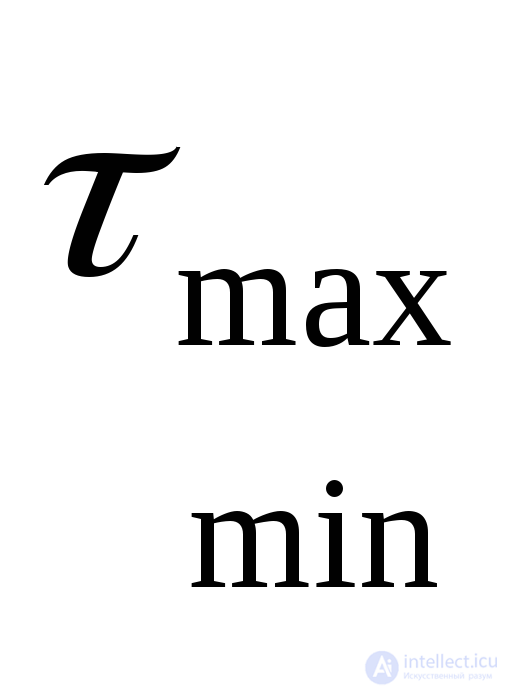 через исходные напряжения
через исходные напряжения и
и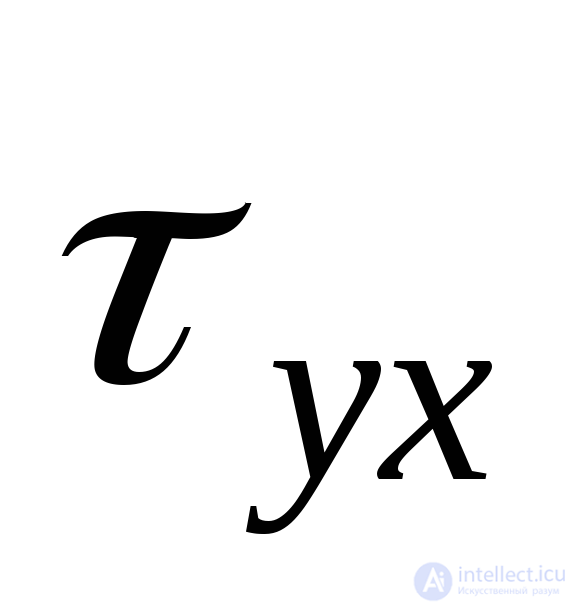 :
:
 . (9.24)
. (9.24)
В частном случае, когда на границах призмы действуют два главных напряжения 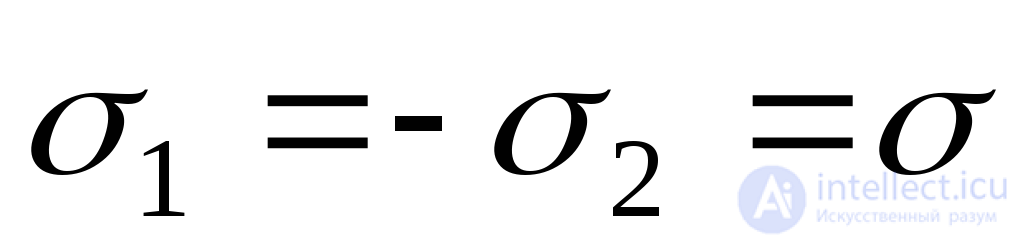 (Рис.9.13б), экстремальные касательные напряжения (9.23) численно равны главным напряжениям:
(Рис.9.13б), экстремальные касательные напряжения (9.23) численно равны главным напряжениям:
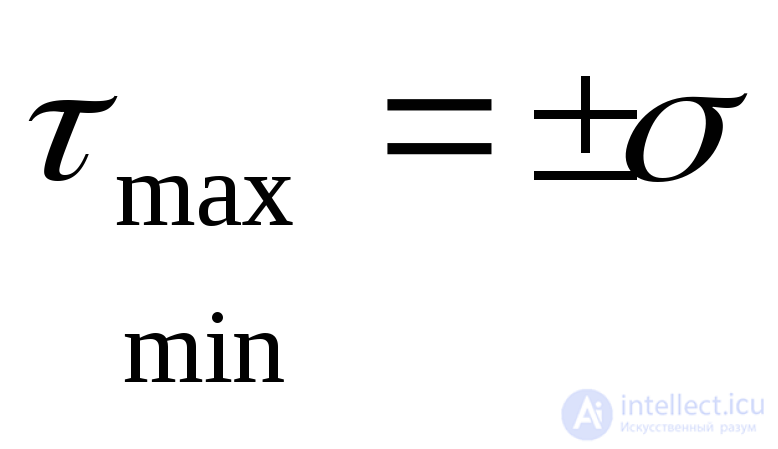 ,
,
а нормальные напряжения на площадках с экстремальными касательными напряжениями в этом случае равны нулю. Такой случай напряженного состояния носит название чистого сдвига, а площадки, на которых действуют одни касательные напряжения называютсяплощадками чистого сдвига.
Пример 9.2.Нормальные напряжения на площадках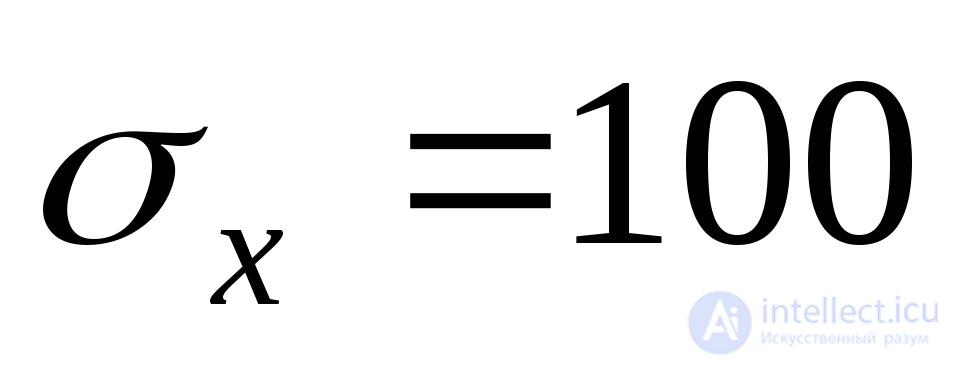 МПа,
МПа,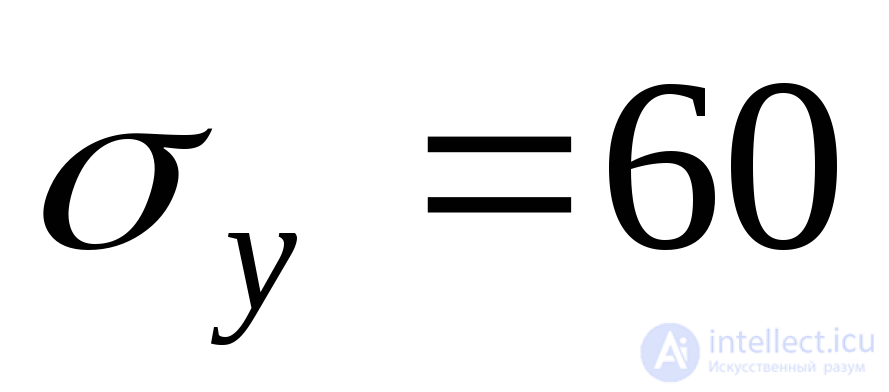 МПа, касательные напряжения
МПа, касательные напряжения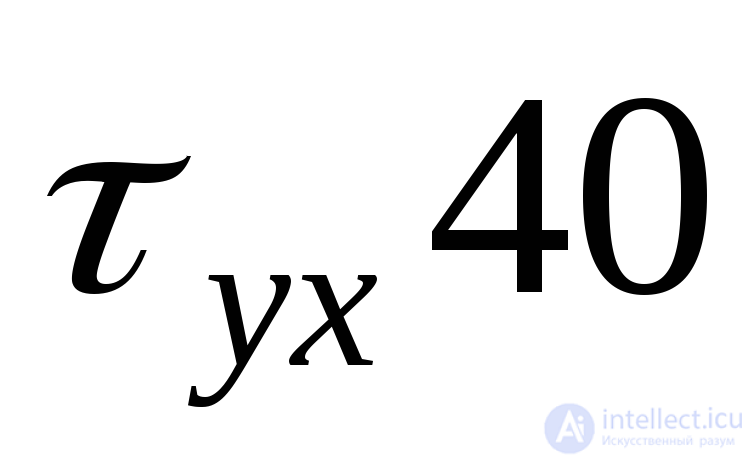 МПа. Определить нормальные
МПа. Определить нормальные ,
, и касательные
и касательные ,
,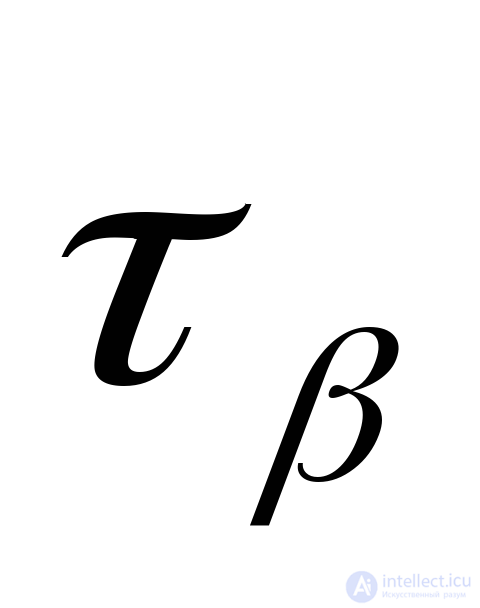 напряжения в площадках, нормаль к которым наклонена по отношению к оси
напряжения в площадках, нормаль к которым наклонена по отношению к оси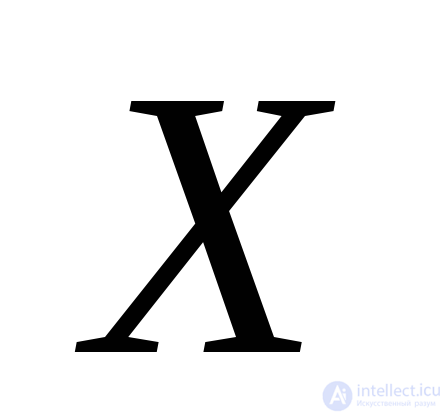 под углами соответственно
под углами соответственно и
и , если
, если =
= ,
, =
=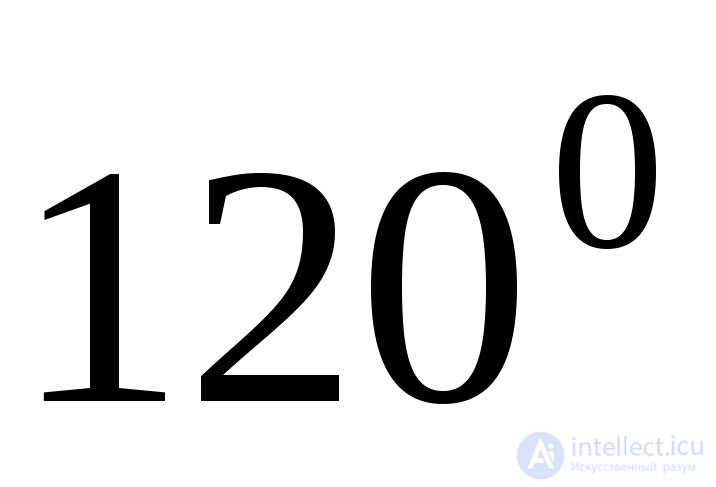 (Рис.9.14).
(Рис.9.14).

Рис.9.14
Решение:
Для определения нормального напряжения в площадке  воспользуемся выражением (9.14):
воспользуемся выражением (9.14):
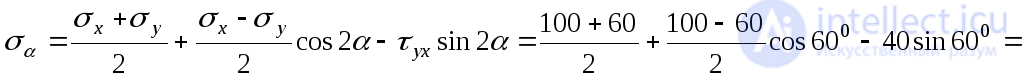
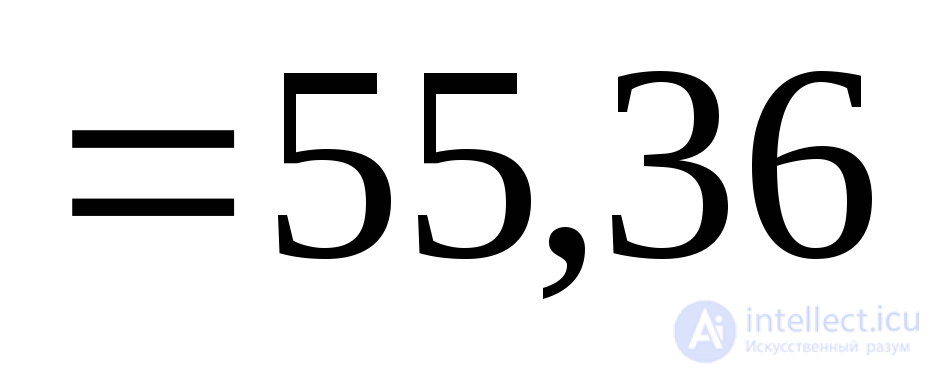 МПа
МПа
Нормальное напряжение вна площадке  найдем с помощью выражения (9.15):
найдем с помощью выражения (9.15):
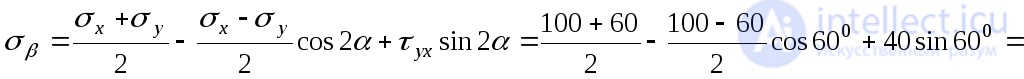
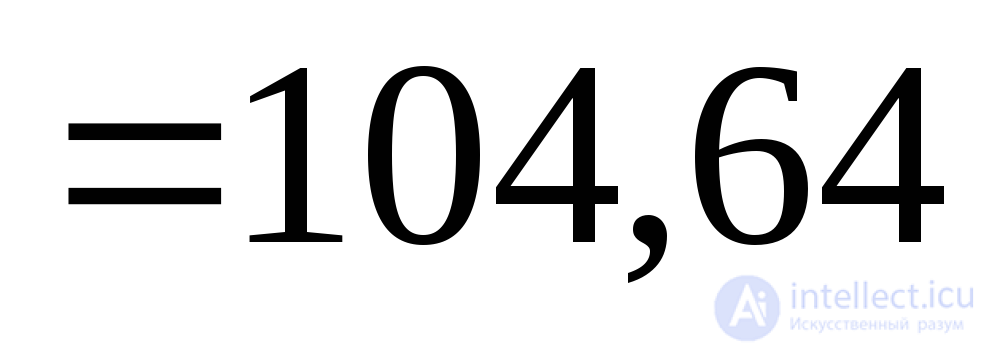 МПа.
МПа.
Для проверки используем условие инвариантности (9.16):
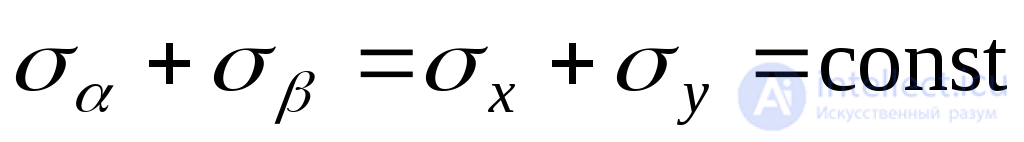 ;
;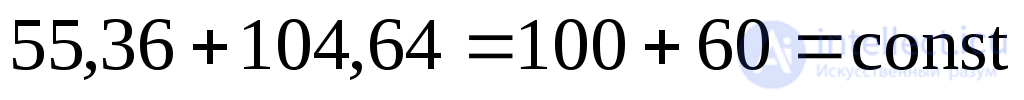 .
.
Касательные напряжения 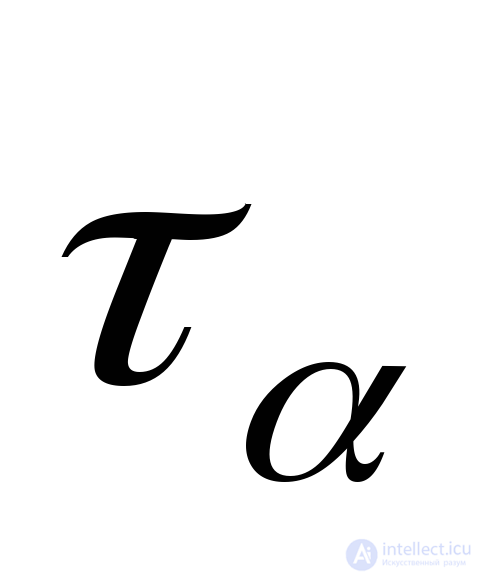 определим из выражения (9.12):
определим из выражения (9.12):
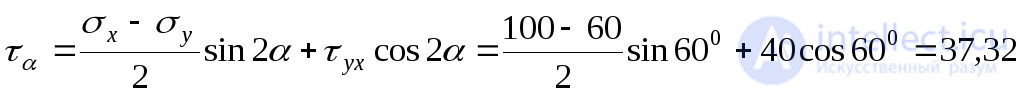 МПа.
МПа.
Касательные напряжения, действующие на площадке  :
:
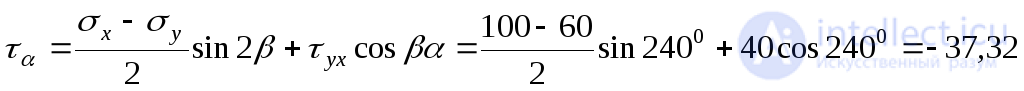 МПа.
МПа.
В соответствии с законом парности касательных напряжений (9.8):
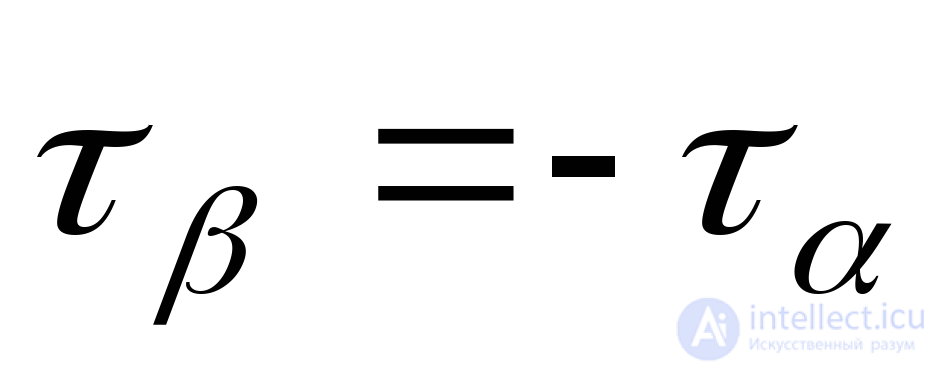 .
.
Следовательно, задача решена верно. Направление нормальных и касательных напряжений, действующих на площадках  и
и покажем на рис 9.15.
покажем на рис 9.15.
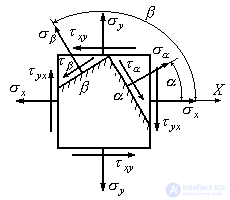
Рис.9.15
Пример 9.3. Определить величины главных напряжений  и
и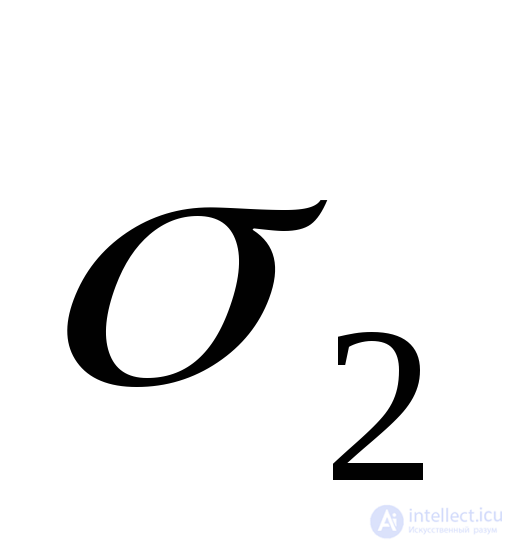 и направления главных напряжений (Рис.9.16,а). Изобразить главные площадки и главные напряжения на рисунке.
и направления главных напряжений (Рис.9.16,а). Изобразить главные площадки и главные напряжения на рисунке.
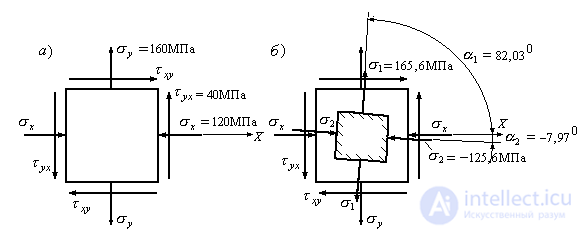
Рис.9.16
Решение:
1. Определяем максимальные нормальные напряжения из выражения (9.19):
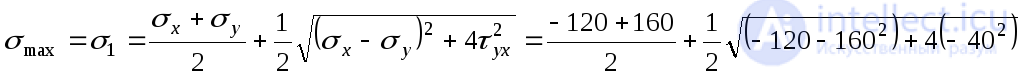 =
=
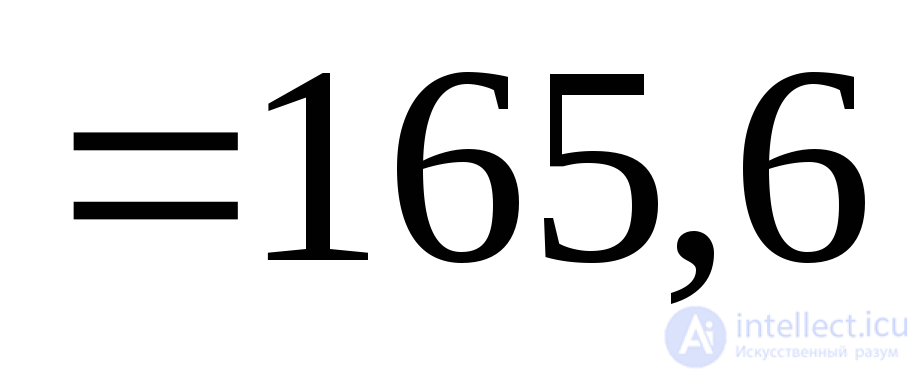 МПа.
МПа.

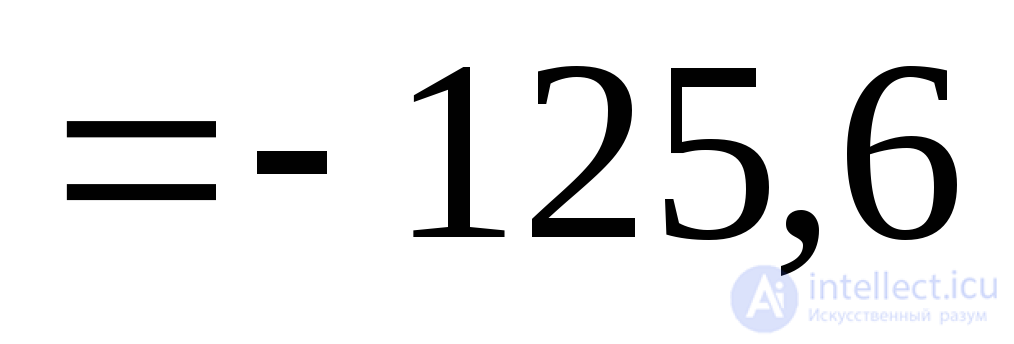 МПа.
МПа.
Для проверки используем условие инвариантности (9.16):
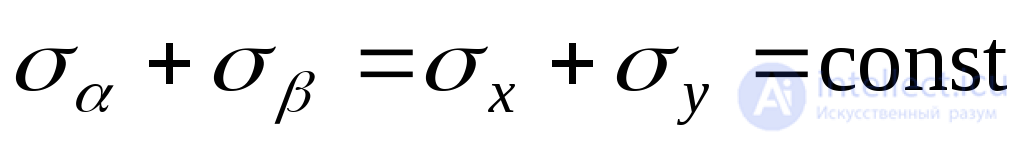 ;
;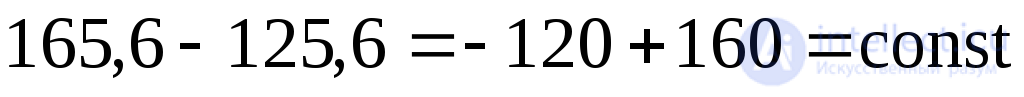 .
.
Направление главных напряжений найдем, используя выражения (9.20):
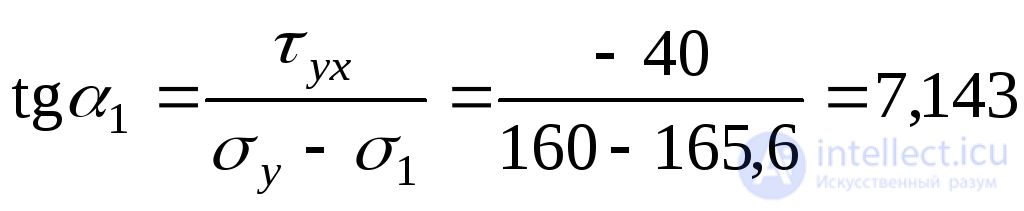 ;
; ;
;
 ;
; .
.
Для проверки правильности решения сложим абсолютные величины углов 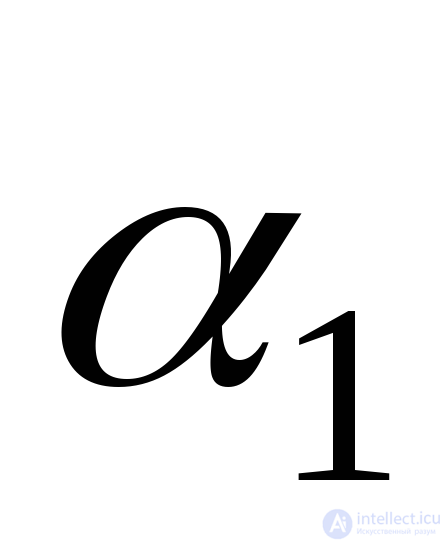 и
и . Так как главные оси взаимно перпендикулярны, в сумме должен получиться угол 900:
. Так как главные оси взаимно перпендикулярны, в сумме должен получиться угол 900:
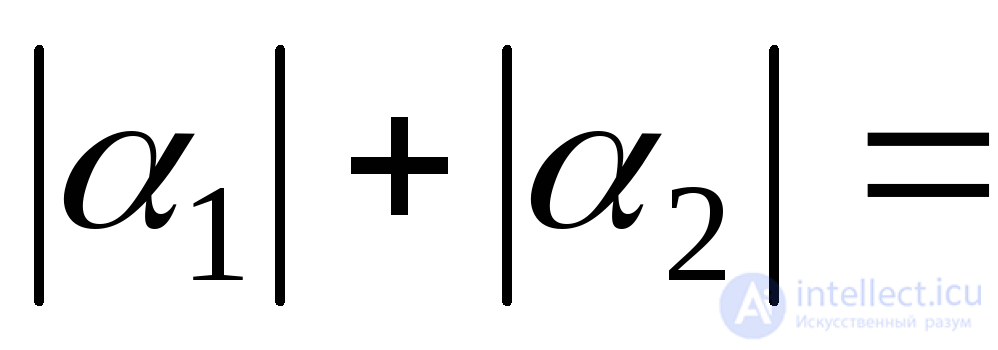
 .
.
Решение выполнено верно. Отложим найденные углы на рисунке (Рис.9.16,б) и проставим значения главных напряжений.
Пример 9.4.Определить нормальные, касательные и главные напряжения в точке А, изображенного на рисунке поперечного сечения изгибаемой балки, если изгибающий момент в сечении равен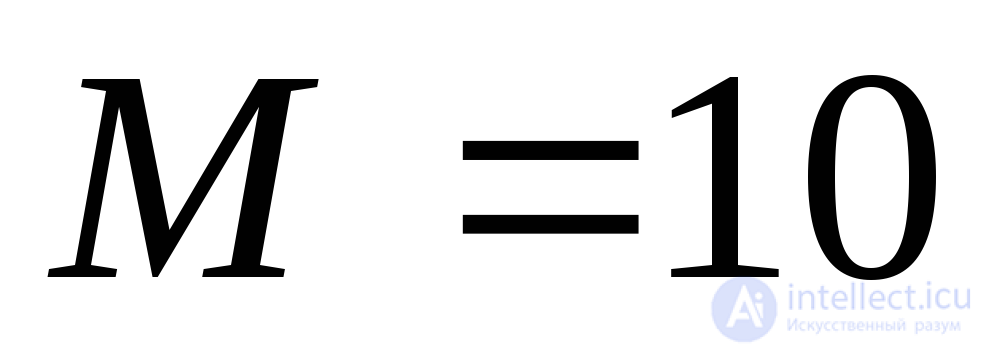 кНм, поперечная сила –
кНм, поперечная сила –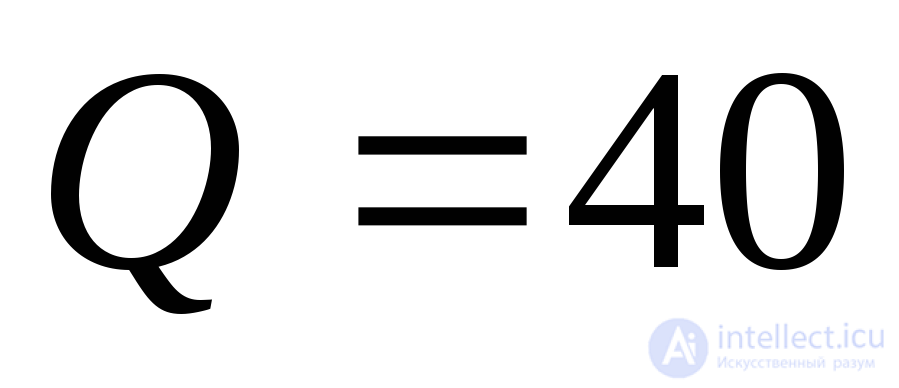 кН. Найти положение главных площадок, изобразить их на рисунке, показать направления главных напряжений.
кН. Найти положение главных площадок, изобразить их на рисунке, показать направления главных напряжений.
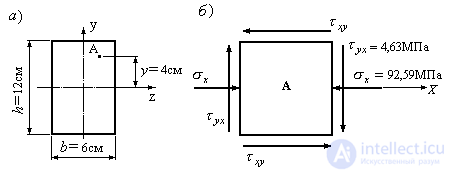
Рис.9.17.
Решение:
1. Вычисляем момент инерции поперечного сечения относительно нейтральной линии сечения  , приведенного на рис 9.17а и определяем величину нормальных напряжений и касательных напряжений в точке А сечения:
, приведенного на рис 9.17а и определяем величину нормальных напряжений и касательных напряжений в точке А сечения:
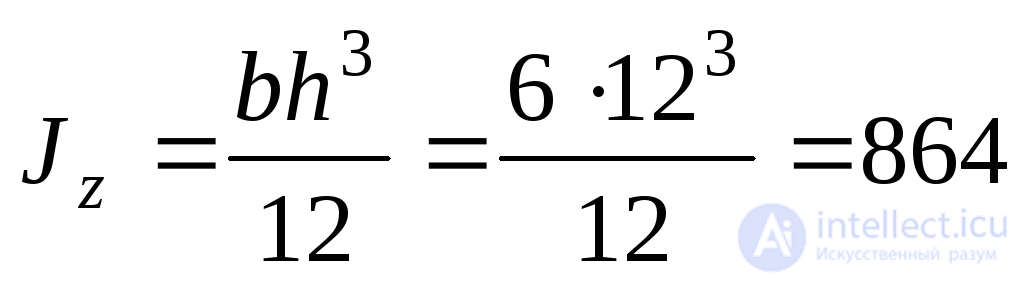 см3;
см3; МПа;
МПа;
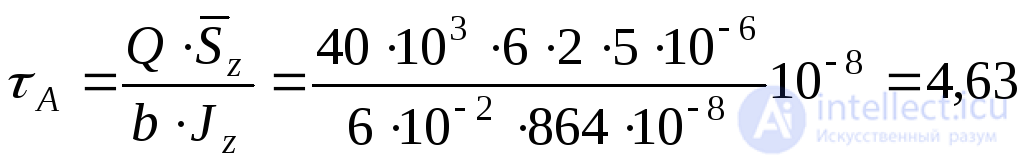 МПа.
МПа.
2. Вырезаем вокруг точки А элементарную площадку и прикладывем к ее граням нормальные и касательные напряжения, действующие в точке А (Рис.9.17б).
3. Определяем главные напряжения в точке А:
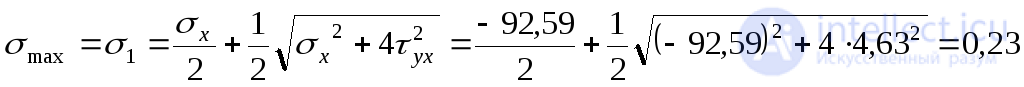 МПа;
МПа;
 МПа.
МПа.
Для проверки используем условие инвариантности (9.16):
 ;
;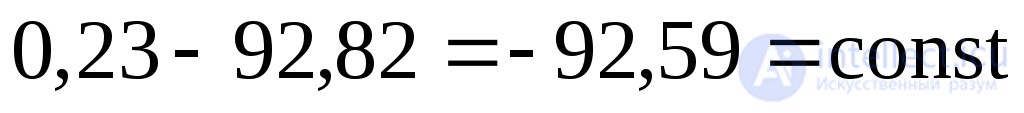 .
.
Направление главных напряжений найдем, используя выражения (9.20):
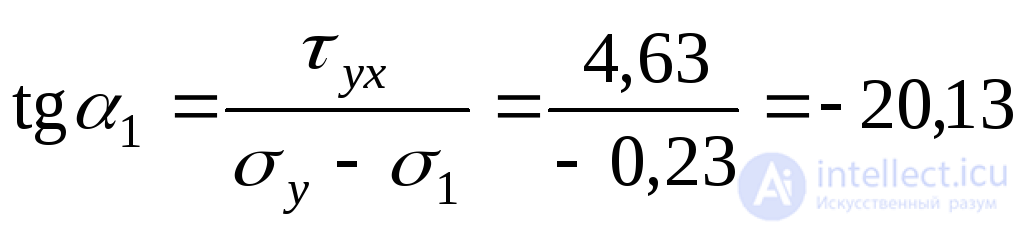 ;
; ;
;
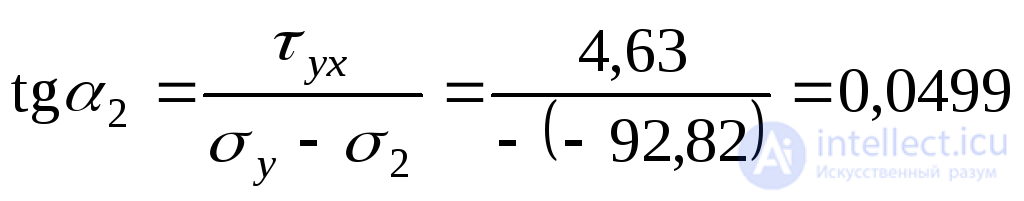 ;
;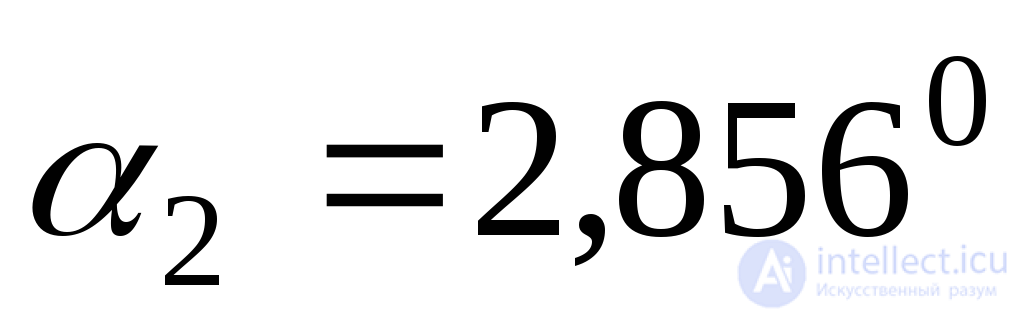 .
.
Для проверки правильности решения сложим абсолютные величины углов  и
и . Так как главные оси взаимно перпендикулярны, в сумме должен получиться угол 900:
. Так как главные оси взаимно перпендикулярны, в сумме должен получиться угол 900:

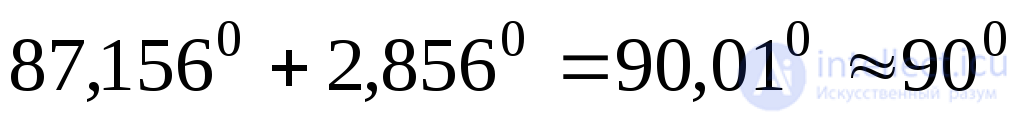 .
.
Решение выполнено верно. Отложим найденные углы на роисунке (Рис.9.18) и проставим значения главных напряжений.
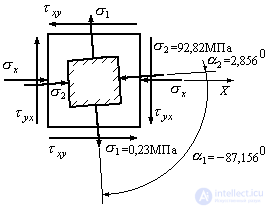
Рис.9.18
Применение знаний о видах напряженного состояния помогает инженерам и ученым анализировать и проектировать конструкции, материалы и механизмы, обеспечивая их надежность и безопасность. Вот несколько примеров применения этих знаний:
Одноосное напряженное состояние: Анализ колонн и балок, находящихся под растяжением или сжатием, помогает определить их прочность и устойчивость.
Двухосное напряженное состояние: Используется для анализа плоских элементов, таких как стены и плиты, под действием нагрузок в двух направлениях.
Трехосное напряженное состояние: Применяется для анализа сложных деталей машин, таких как зубчатые колеса и подшипники, которые испытывают многоосные нагрузки.
Чистое сдвиговое напряженное состояние: Важно при проектировании соединений, таких как резьбовые соединения и сварные швы.
Одноосное напряженное состояние: Используется для расчета элементов конструкций самолетов и космических аппаратов, подверженных растяжению или сжатию.
Двухосное напряженное состояние: Актуально для анализа обшивки и панелей, подвергающихся нагрузкам в двух направлениях.
Трехосное напряженное состояние: Важно при проектировании сосудов под давлением и трубопроводов, испытывающих многоосные нагрузки из-за внутреннего давления.
Чистое сдвиговое напряженное состояние: Применяется для анализа материалов, используемых в турбинах и генераторах.
Одноосное напряженное состояние: Используется для анализа костей и имплантатов, испытывающих продольные нагрузки.
Двухосное напряженное состояние: Важно при исследовании тканей и биоматериалов, используемых в медицинских устройствах.
Проектирование мостов: Инженеры используют знания о напряженных состояниях для расчета сил, действующих на различные элементы моста (колонны, балки и тросы), чтобы обеспечить его устойчивость и долговечность.
Разработка автокомпонентов: В автомобильной промышленности анализ напряженного состояния помогает в проектировании безопасных и надежных кузовов, шасси и двигателей.
Проектирование космических аппаратов: В аэрокосмической инженерии анализ трехосного напряженного состояния позволяет создавать конструкции, способные выдерживать высокие нагрузки и экстремальные условия в космосе.
Эти примеры демонстрируют, как знания о видах напряженного состояния помогают решать практические задачи в различных областях инженерии и науки.
Анализ данных, представленных в статье про плоское напряженное состояние, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое плоское напряженное состояние, напряженное состояние и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов
Комментарии
Оставить комментарий
Сопротивление материалов
Термины: Сопротивление материалов