Привет, Вы узнаете о том , что такое деформированное состояние в точке, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое деформированное состояние в точке , настоятельно рекомендую прочитать все из категории Сопротивление материалов.

9.5.1. Понятие о тензоре и девиаторе тензора деформаций. Главные линейные деформации

деформированное состояние в точке описывает изменение формы и размеров материала в небольшой области (точке) под воздействием внешних сил и моментов.

Деформация любого элементарного параллелепипеда может быть представлена состоящей из ряда отдельных простейших деформаций (Рис.9.23). Всего составляющих деформации шесть: три линейных (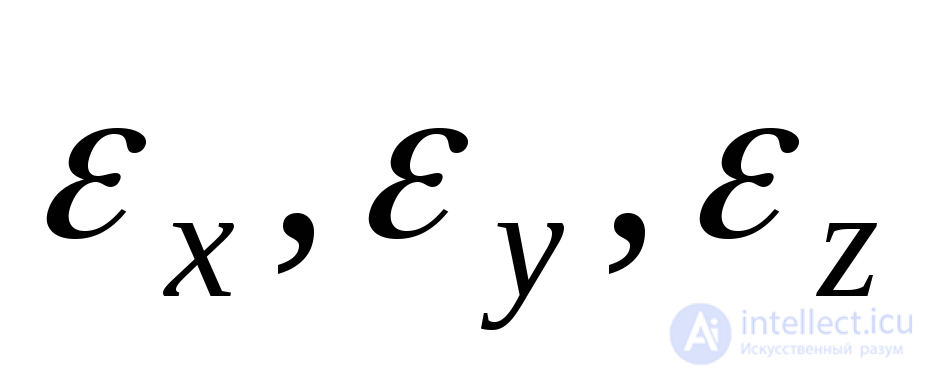) и три угловых, сдвиговых (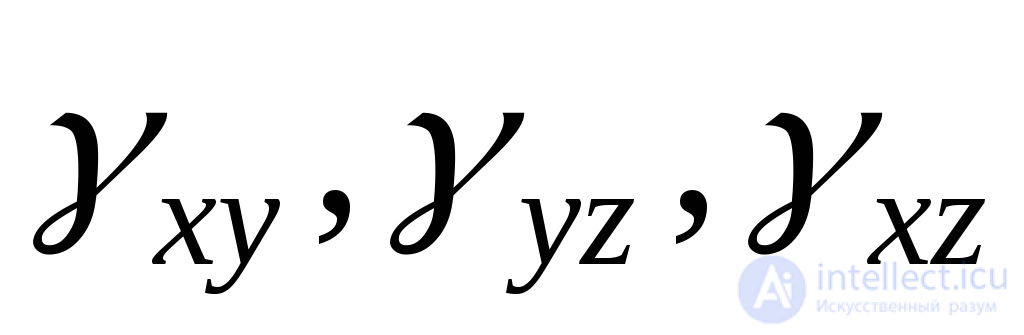). Линейные составляющие представляют собой относительное удлинение ребер элементарного параллелепипеда, а индекс при обозначении деформаций показывает, параллельно какой оси имеет место это удлинение. Линейные деформации приводят к изменению объема и формы (например, переход от формы куба к форме параллелепипеда). Угловые деформации представляют собой сдвиг элементарного параллелепипеда по отношению к первоначальному положению. Положительному сдвигу соответствует уменьшение угла между положительным направлением осей, отрицательному – увеличение этого угла.

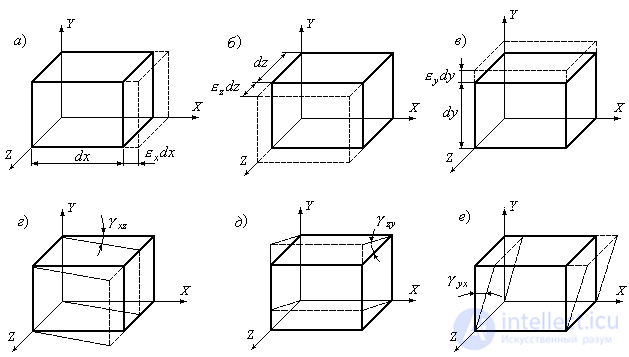
Рис.9.23

Углы сдвига, проектируемые на плоскость ХY, обозначаются 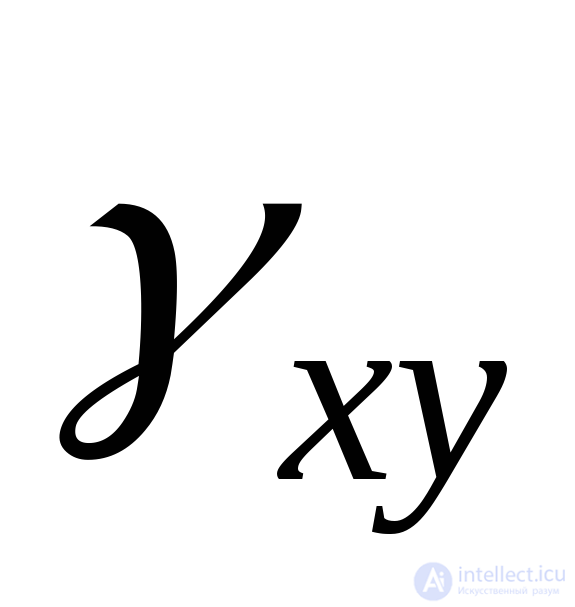(или), на плоскостьYZ (или 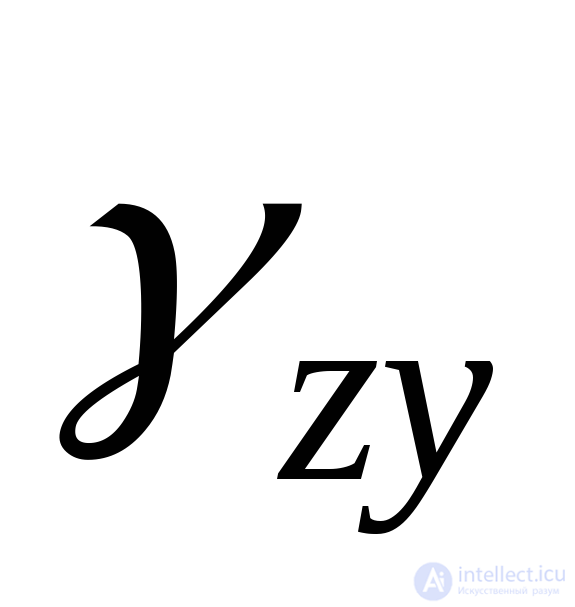) и на плоскостьZX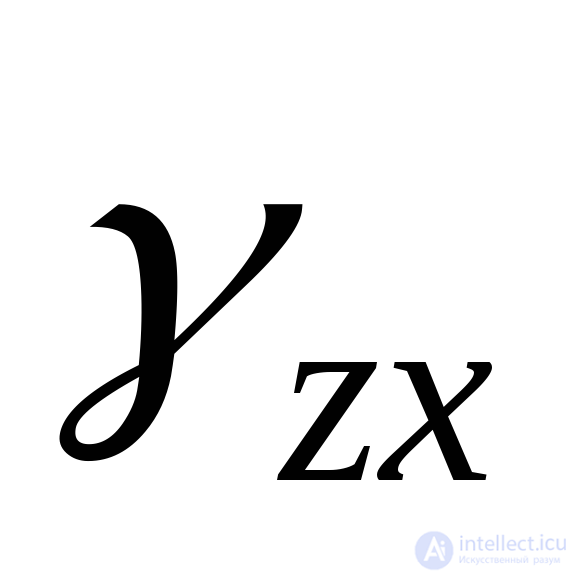(или). При этом угловые деформации попарно равны: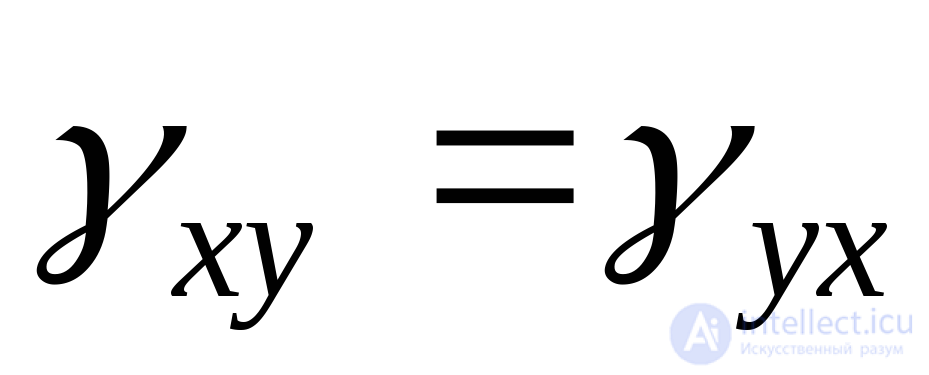;;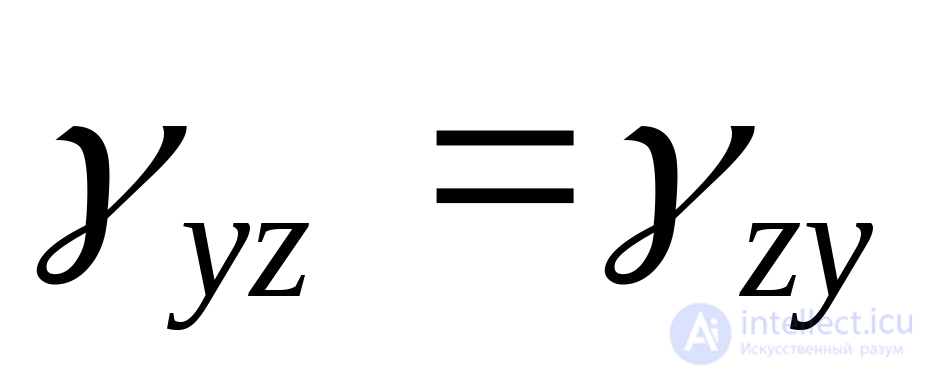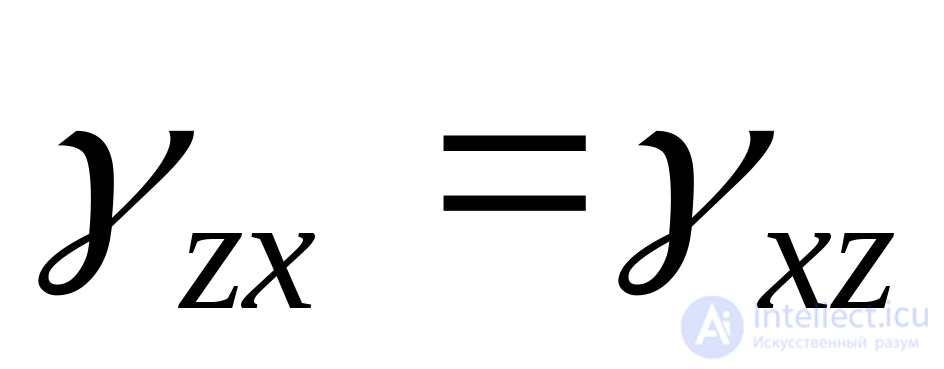. Таким образом, деформированное состояние, представляющее собой совокупность линейных и угловых деформаций для всевозможных положений осей координат, в общем случае может быть описано тензором деформаций:, включающий в себя девять компонентов: три относительные линейные деформации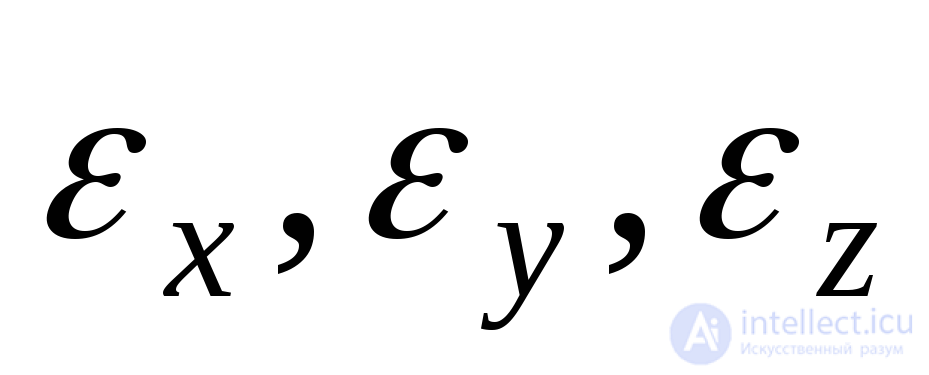и шесть углов сдвига,,.

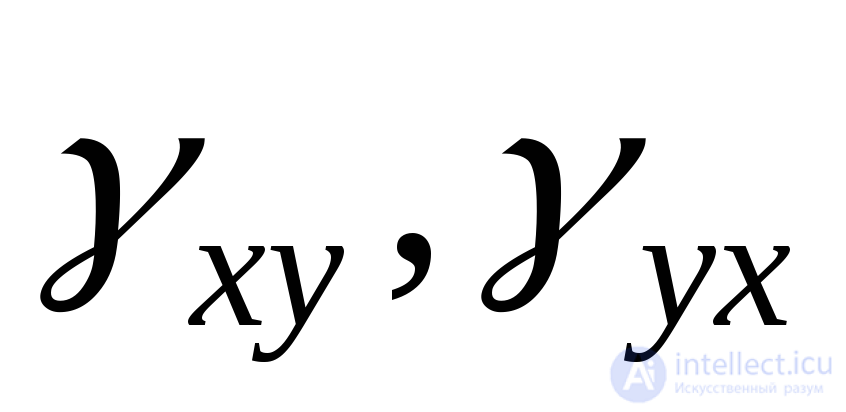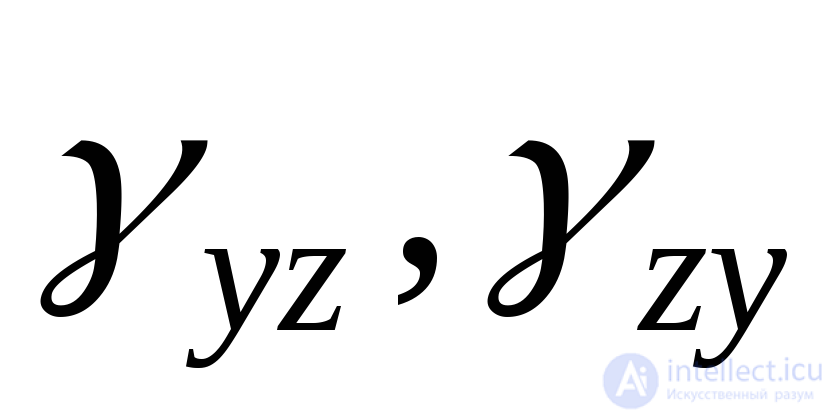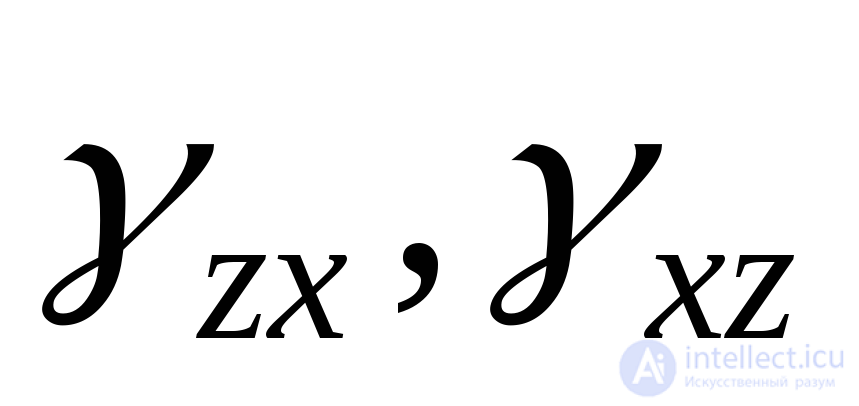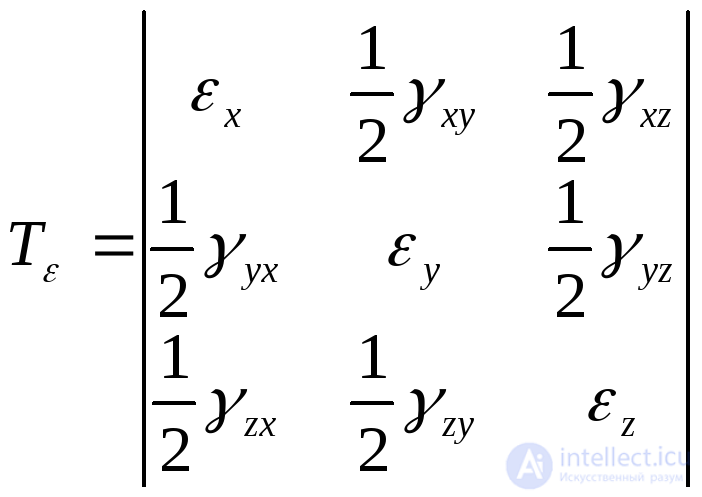. (9.54)

Тензор деформаций можно разделить на шаровой тензор деформаций

. (9.55)

который характеризует объемную деформацию в точке, и на девиатор деформаций:

, (9.56)

который характеризует формоизменение в окрестности этой же точки.

Удлинение какого-либо отрезка, проходящего через данную точку, можно выразить через шесть компонент деформации той же точки

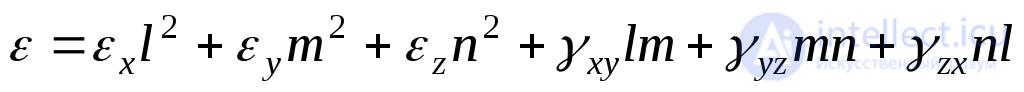, (9.57)

где 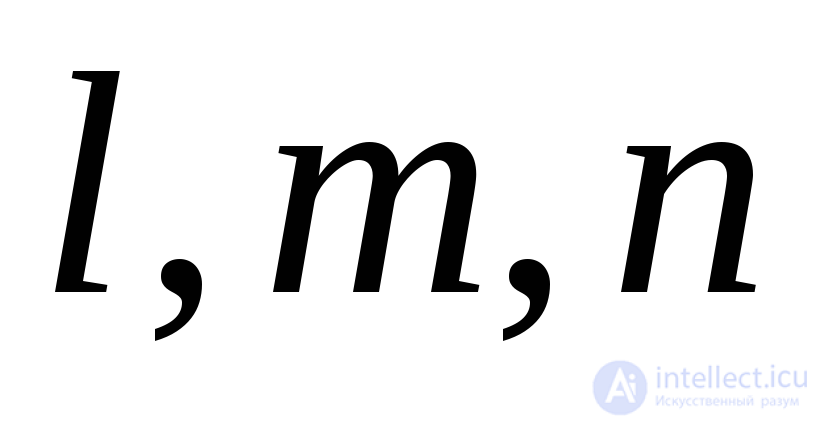косинусы между направлением рассматриваемого отрезка и осями прямоугольных координат.

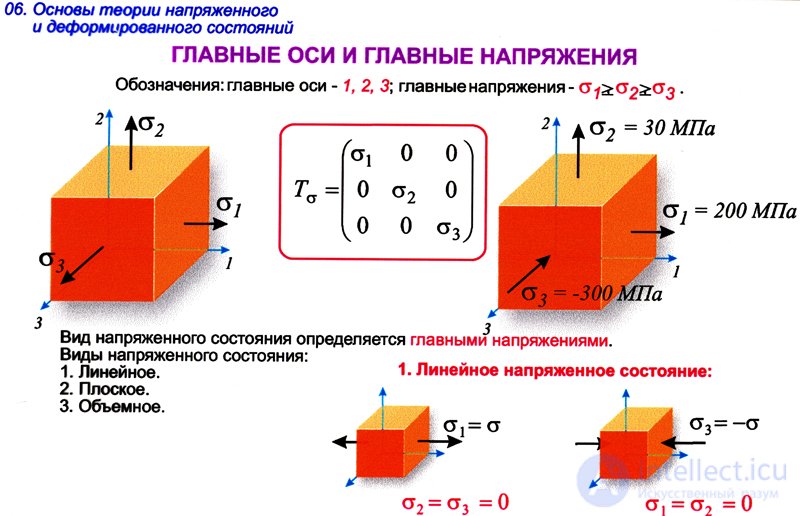
Можно утверждать, что в каждой точке (по аналогии с напряженным состоянием) тела существуют три взаимно перпендикулярных направления, называемые главными осями деформаций, которые обладают тем свойством, что материал по этим направлениям испытывает только линейные деформации, так как сдвиги при этом равны нулю.

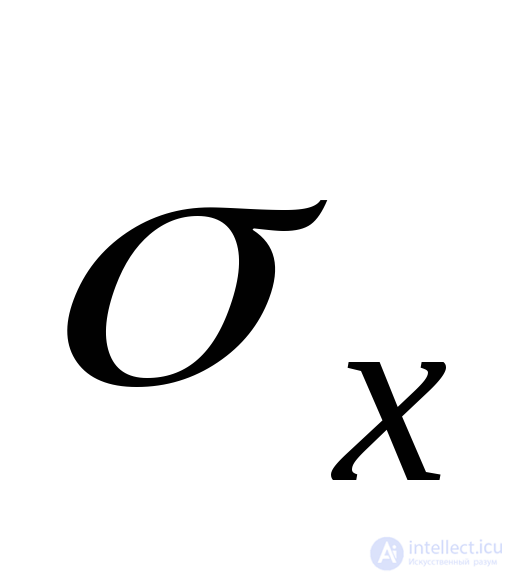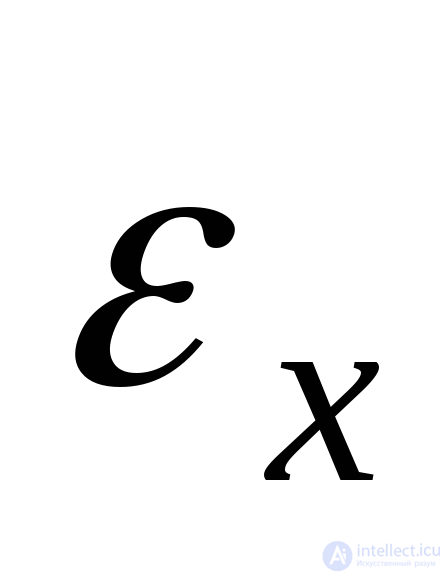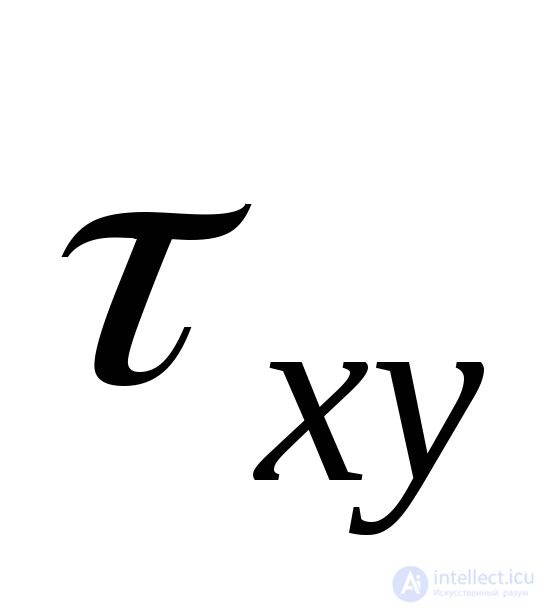Если подставить в (9.35) вместо компонент тензора напряжений компонениы деформаций, т.е. изменить на,наи т.д., то можно получить кубическое уравнение, определяющее главные линейные деформации:

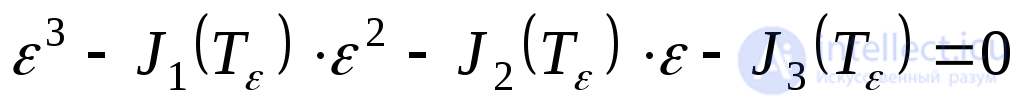. (9.58)

Инварианты тензора деформаций будут иметь вид:

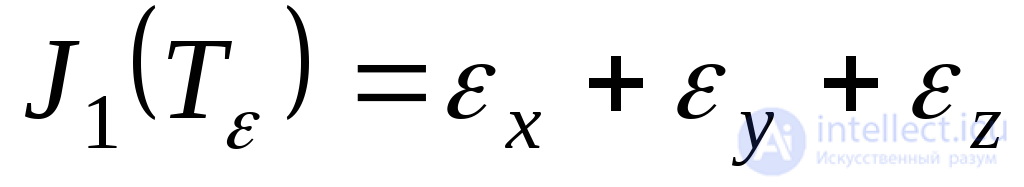; (9.59)

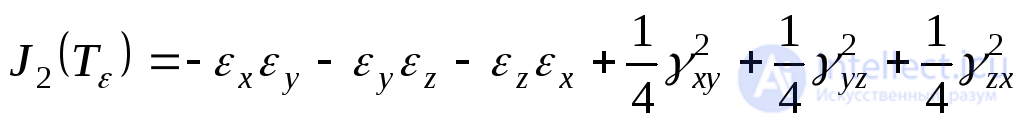;(9.60)

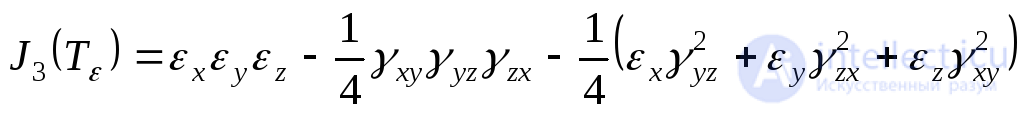. (9.61)

Выражения инвариантов через главные деформации имеют вид:

; (9.62)

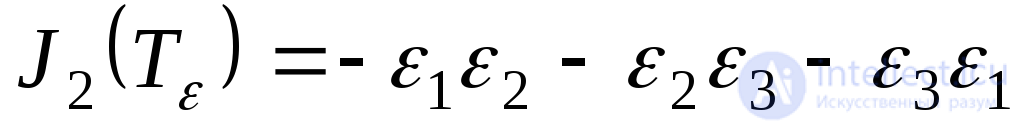;(9.63)

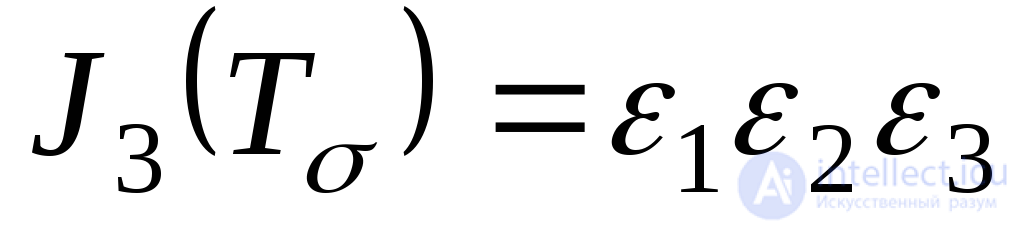.(9.64)

По аналогии с напряжениями, удлинение в направлении, перпендикулярном к октаэдрическим площадке, будет равно:

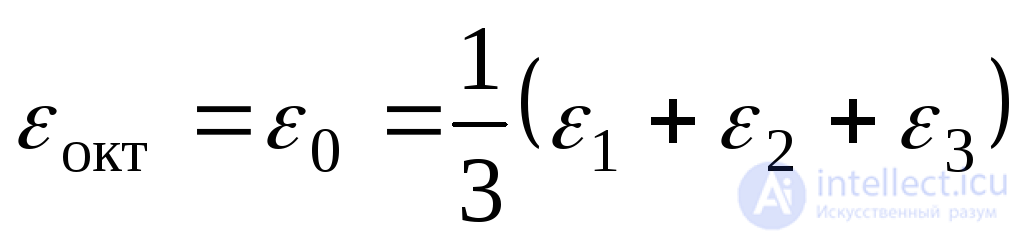. (9.65)

Относительная угловая деформация в октаэдрических плоскостях имеет вид:

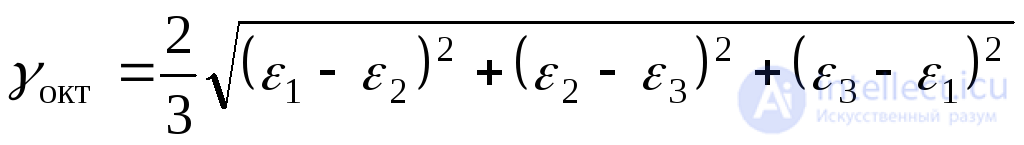(9.66)

или

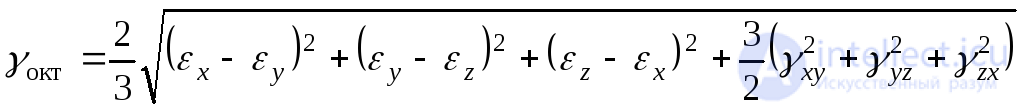(9.67)

Наибольший относительный сдвиг по аналогии с (9.43) равен:

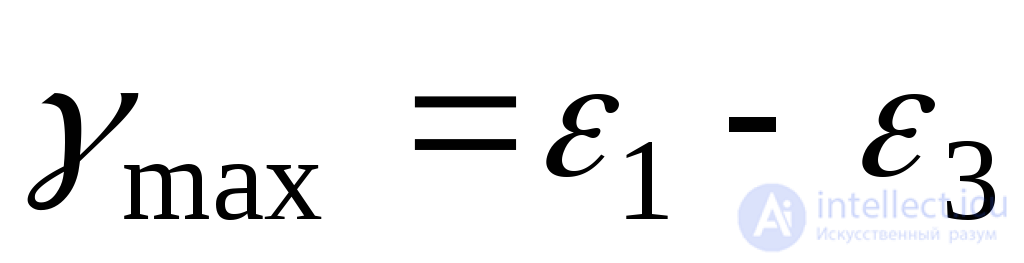. Об этом говорит сайт https://intellect.icu . (9.68)

Интенсивность деформаций надем из выражения:

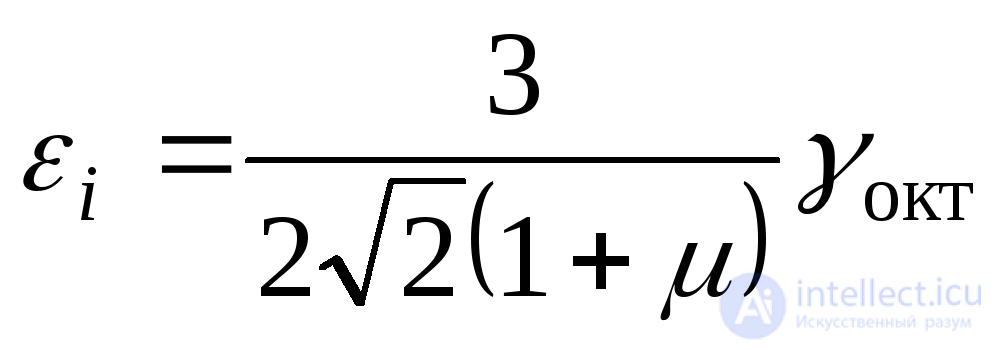(9.69)

или

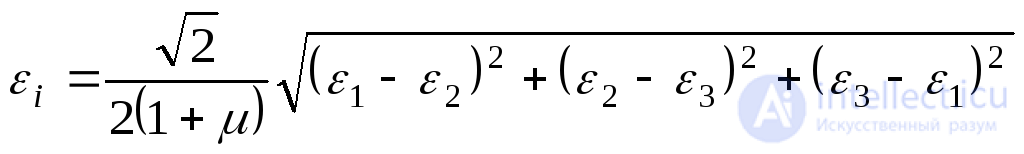. (9.70)

Здесь коэффициент Пуассона.

9.5.2. Закон Гука при плоском и объемном напряженном состоянии

Рассмотрим элемент, выделенный из центрально растянутого стержня (Рис.9.24).

Рис.9.24

Элемент испытывает продольную и поперечную деформации, связанные с напряжениями формулами:

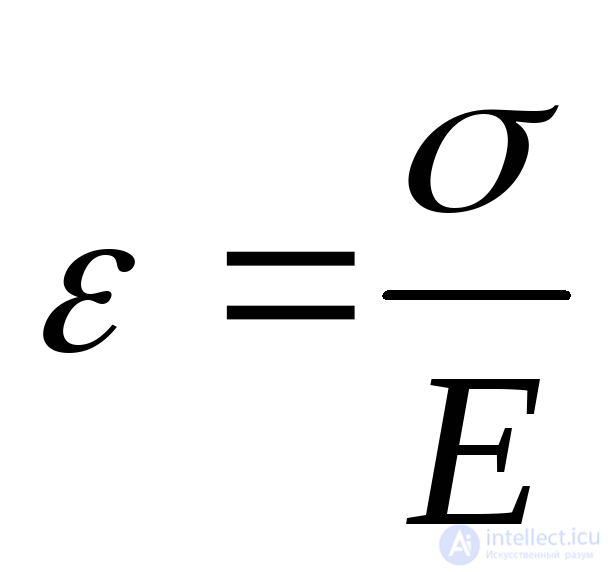; (9.71)

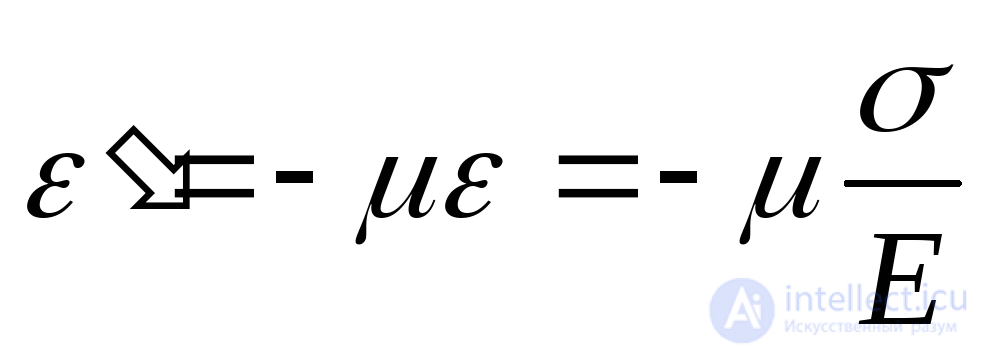. (9.72)

Здесь: модуль упругости при растяжении (сжатии), акоэффициент Пуассона. Деформация удлинения считается положительной, укорочения – отрицательной.

Формула (9.71) выражает закон Гука при простом растяжении (линейное напряженное состояние). Установим аналогичное соотношение при объемном напряженном состоянии.

Найдем главные деформации 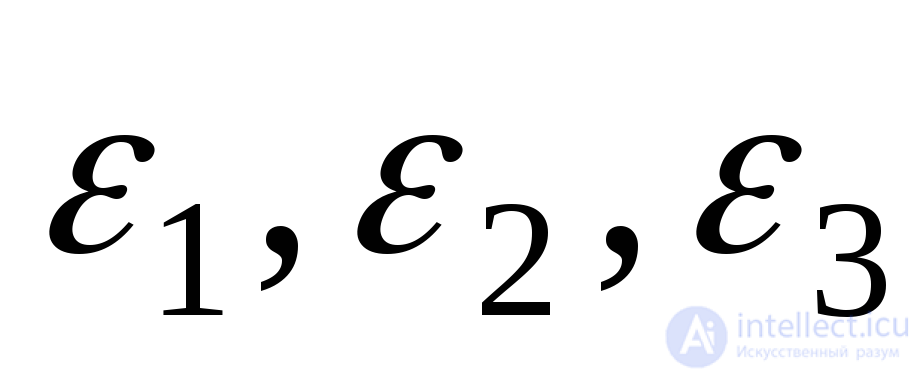, выразив их через главные напряжения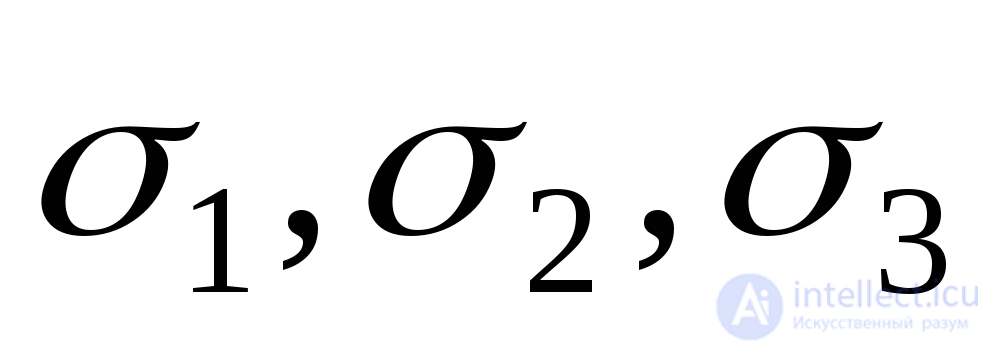. Для этого воспользуемся принципом независимости действия сил и соотношениями (9.71) и (9.72). Суммарное относительное удлинение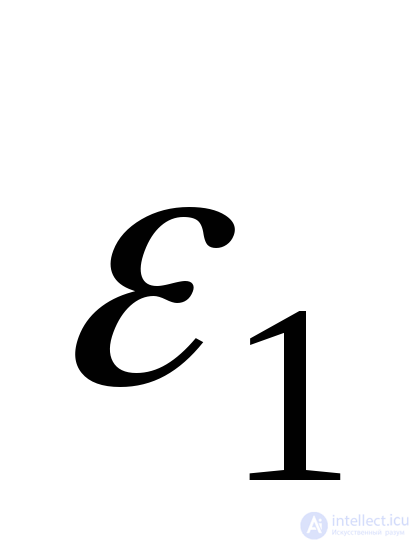по направлению напряжения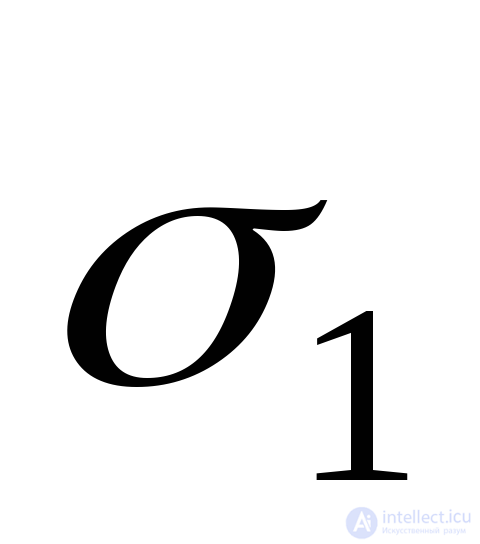можно представить тремя слагаемыми:

,

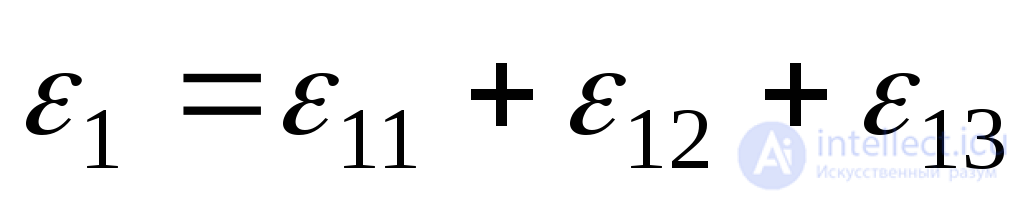где деформация, возникающая при действии только напряжения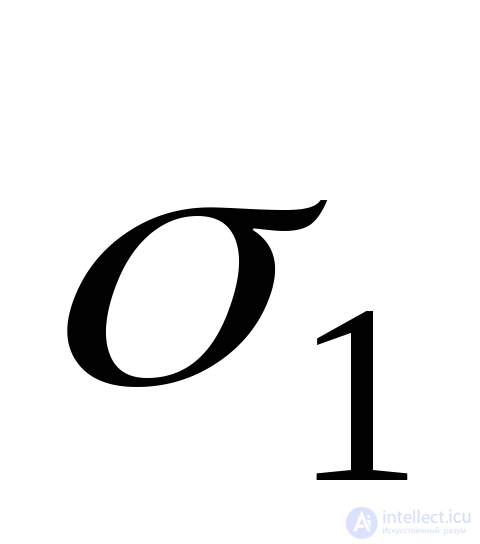и определяемая по формуле (9.71), так как эта деформация является продольной по отношению к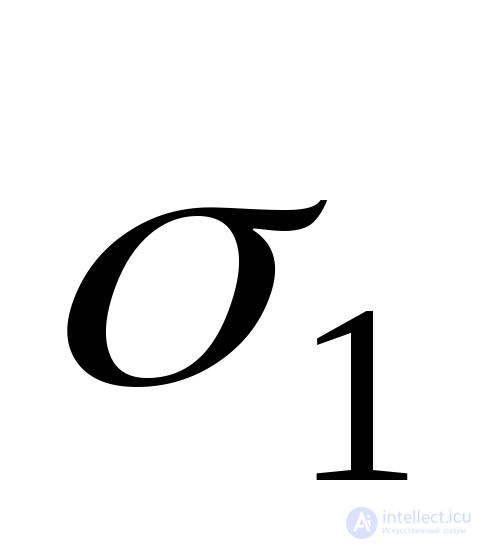(Рис.9.25а).

 удлинение, вызванное напряжением. Это поперечнае по отношению к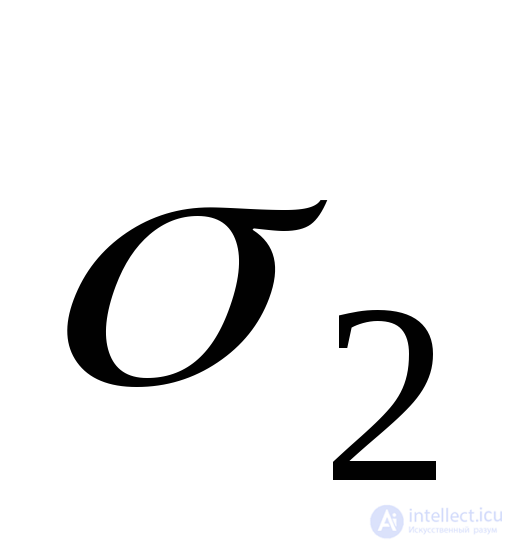деформация (Рис.9.25б), которая определяется по формуле (9.72).

 деформация, вызванная напряжением.

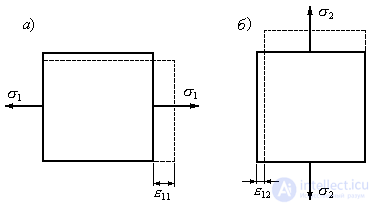
Рис.9.25

Следовательно:

.

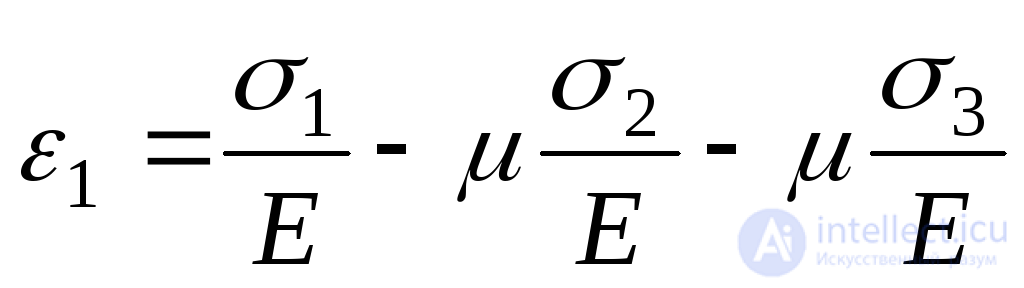Применяя подобные рассуждения к определению и, получим формулы закона Гука при объемном напряженном состоянии (обобщенный закон Гука):

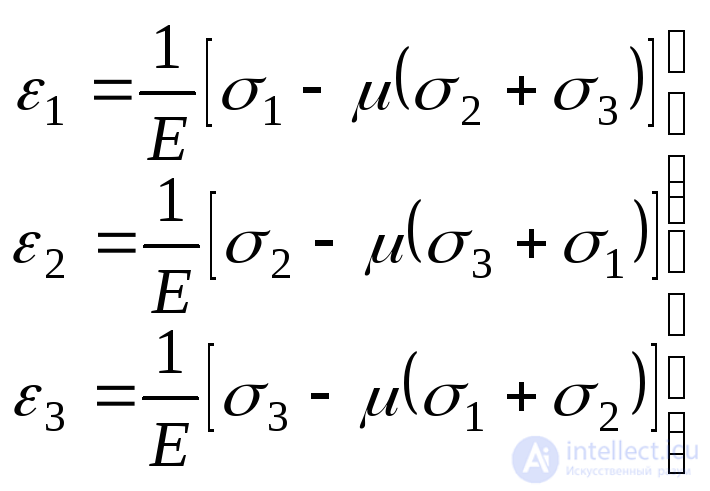. (9.73)

В эти формулы растягивающее напряжение подставляется со знаком “плюс”, а сжимающие – со знаком“минус”.

При равенстве нулю одного из трех главных напряжений имеем плоское напряженное состояние. В этом случае, например, при 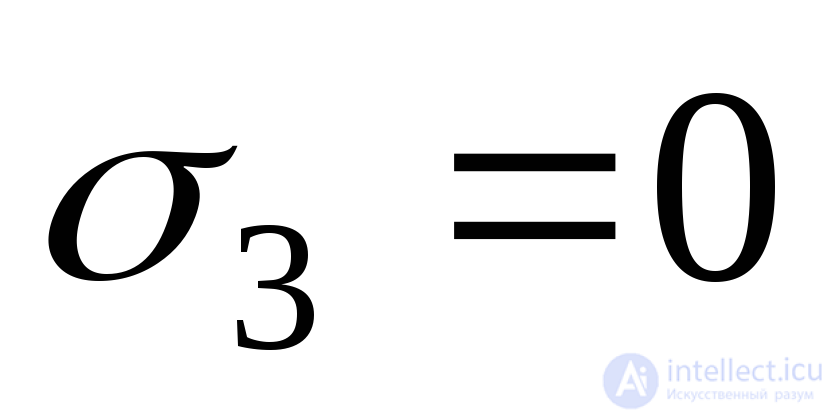, получим:

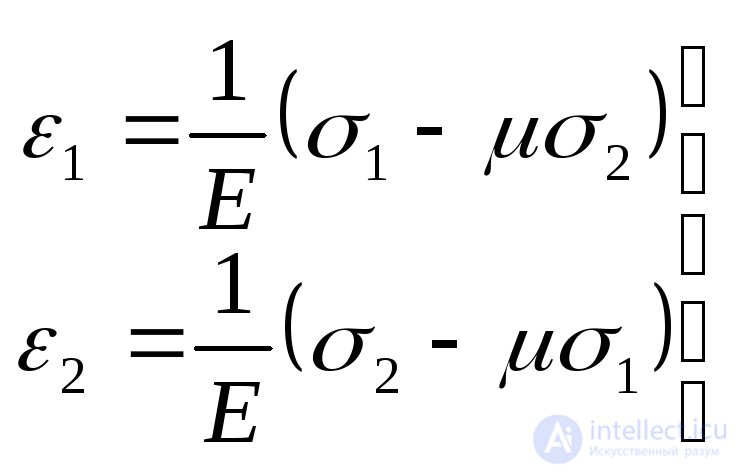.(9.74)

Следует отметить, что равенство нулю напряжения не означает, что также равно нулю. Действительно, при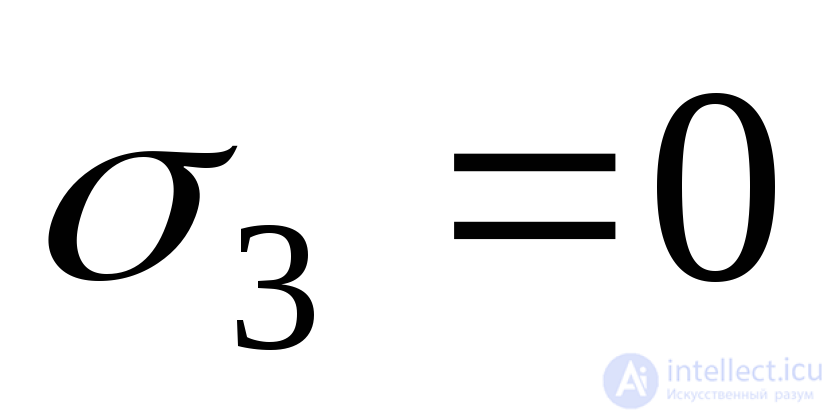имеем:

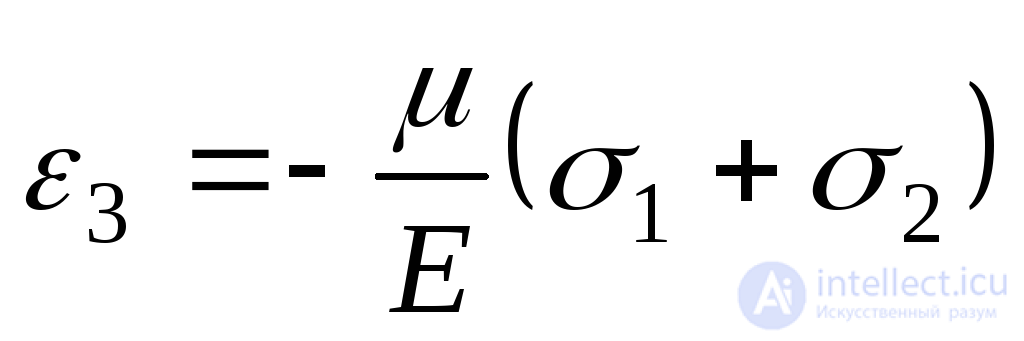. (9.75)

При известных напряжениях 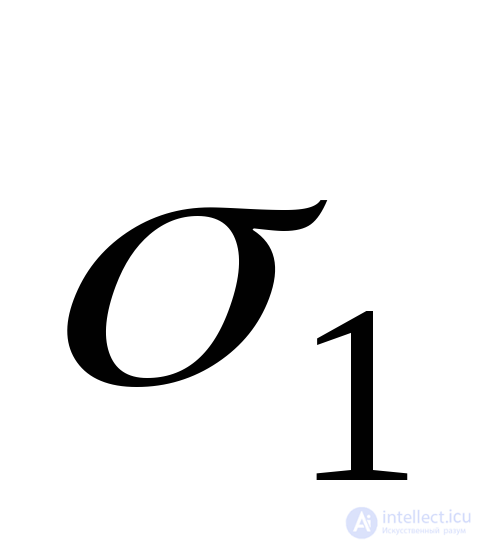и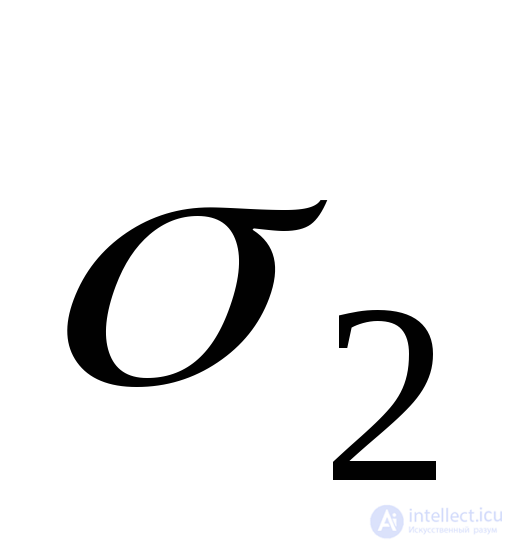по формулам (9.74) определяют дефомациии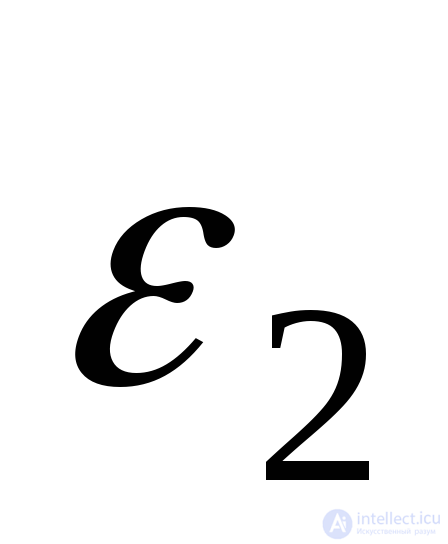. Но в некоторых случаях необходимо иметь обратную зависимость. Умножая вторую строку формулы (9.74) наи складывая с первой, получим:

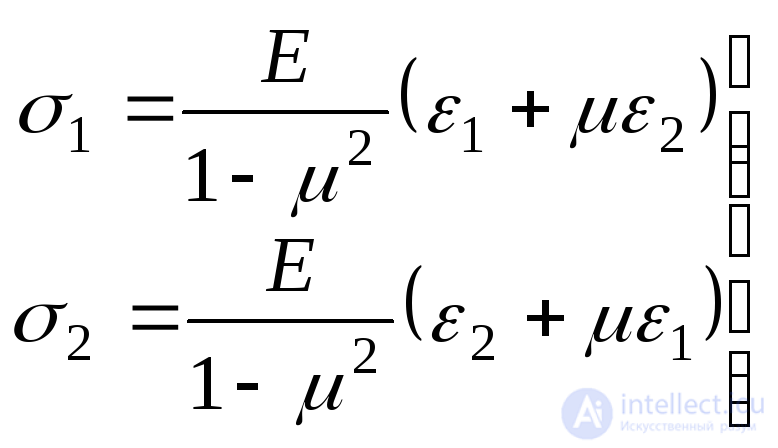.(9.76)

Полученные формулы написаны применительно к главным площадкам и напряжениям. Однако, следует иметь ввиду, что и для неглавных площадок закон Гука, связывающий нормальные напряжения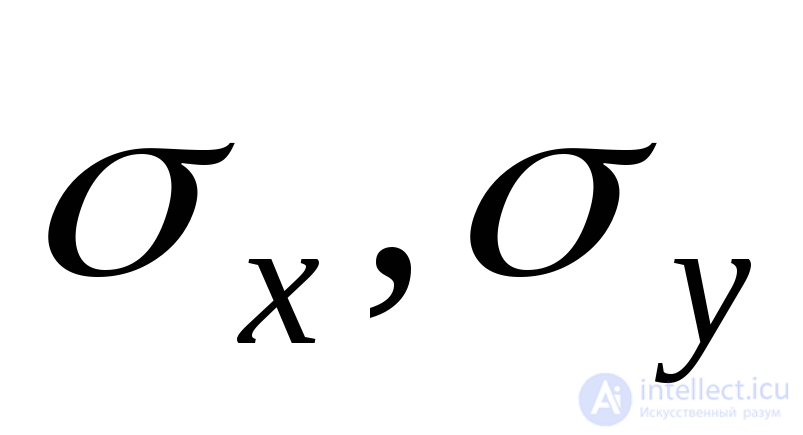и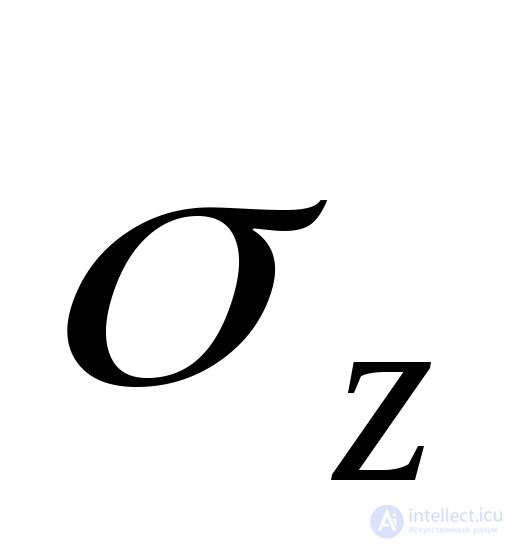и соответствующие удлинения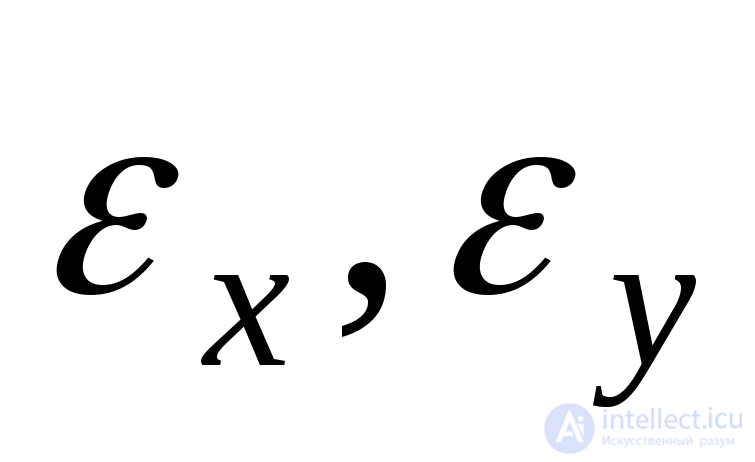и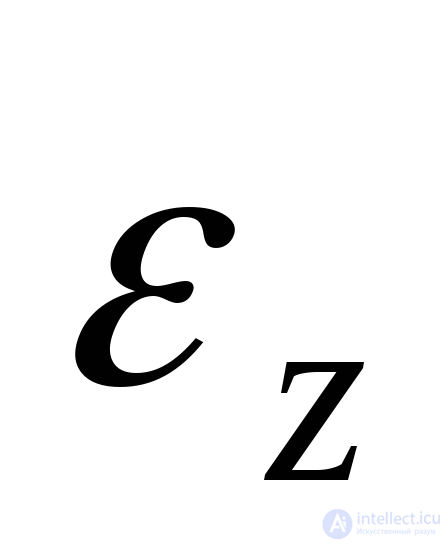, имеет тот же вид:

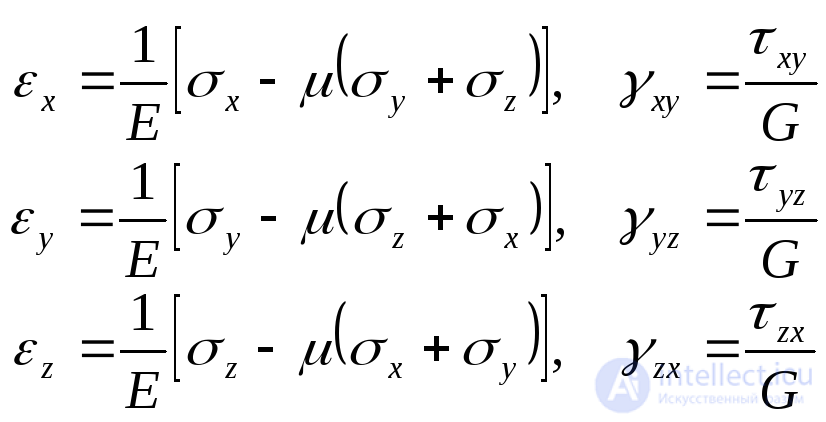, (9.77)

где модуль сдвига.

Причина состоит в том, что при малых деформациях влияние сдвига на линейную деформацию представляет собой величину второго порядка малости, которой можно пренебречь.

9.5.3.Объемная деформация. Объемный закон Гука

Обозначим размеры сторон элементарного параллелепипеда до деформации через 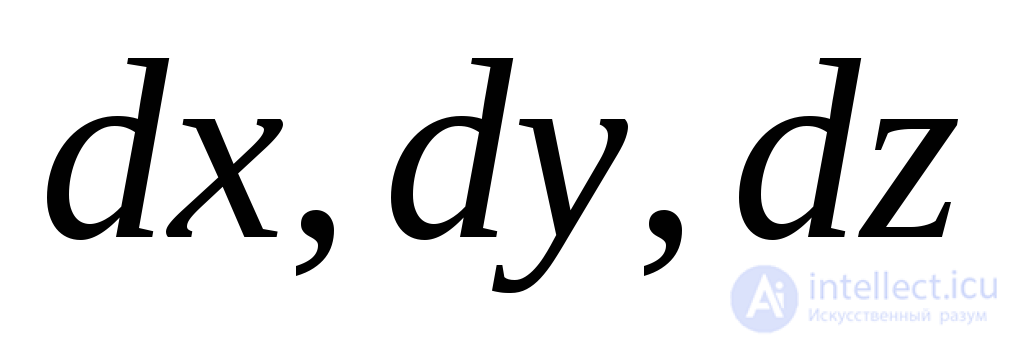(Рис.9.26а). После деформации эти размеры увеличатся и станут равными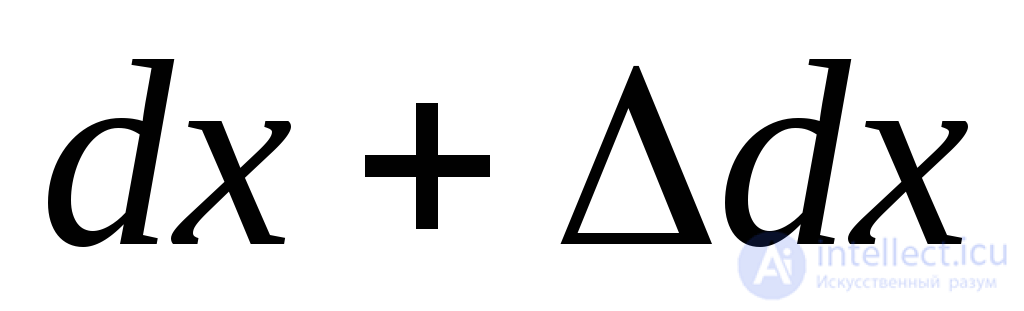,,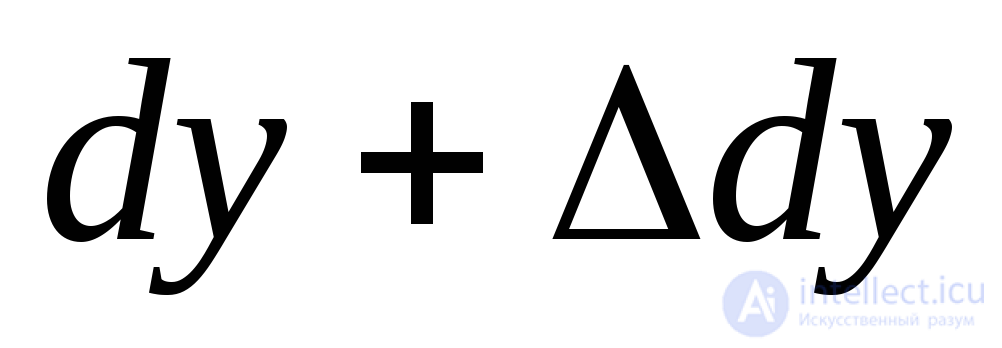(Рис.9.26б). Начальный объем параллелепипеда обозначим, а после деформации.

Найдем абсолютное изменение объема параллелепипеда:

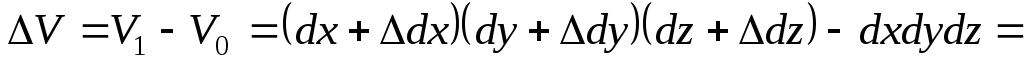
. (9.78)

Здесь в скобках стоят относительные удлинения:

. (9.79)

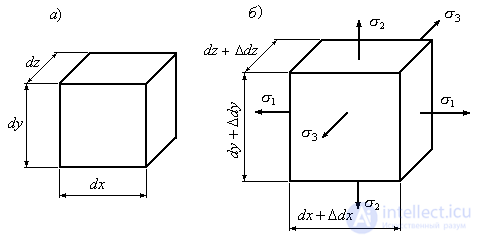
Рис.9.26

Подставляя в (9.79) в (9.78) и перемножая выражения в скобках, получаем:

.

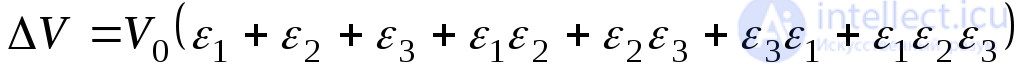Пренебрегая произведениями относительных удлинений ввиду их малости, имеем:

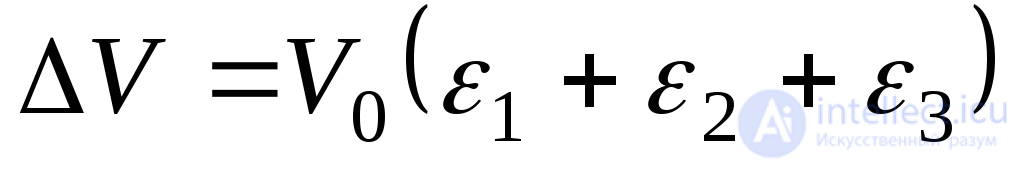(9.80)

Относительное изменение объема или относительная объемная деформация принимает вид:

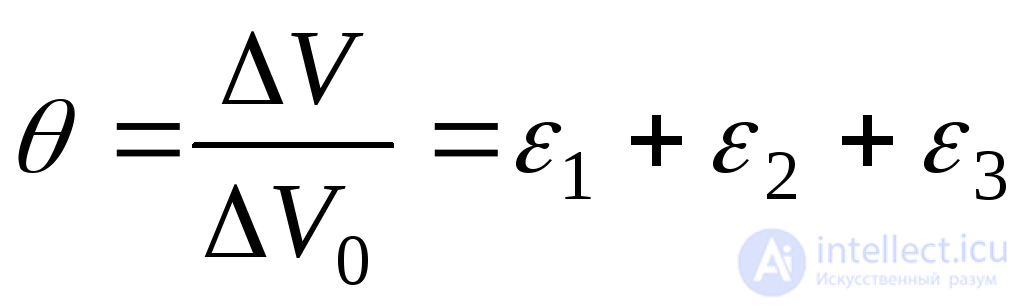. (9.81)

Эта формула справедлива как для упругих, так и для упруго-пластических деформаций.

Для упругой стадии работы материала можно выразить относительное изменение объема через напряжения 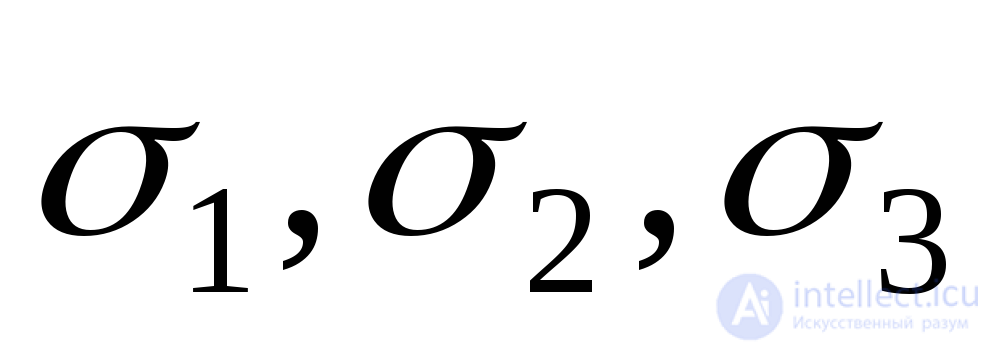. Для этого подставим значенияиз выражения (9.73) в выражение (9.81):

.

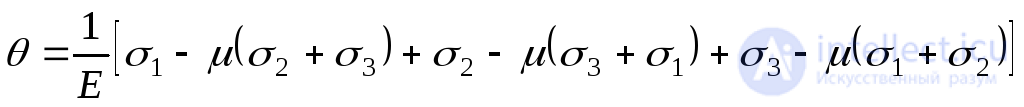После преобразования, получим:

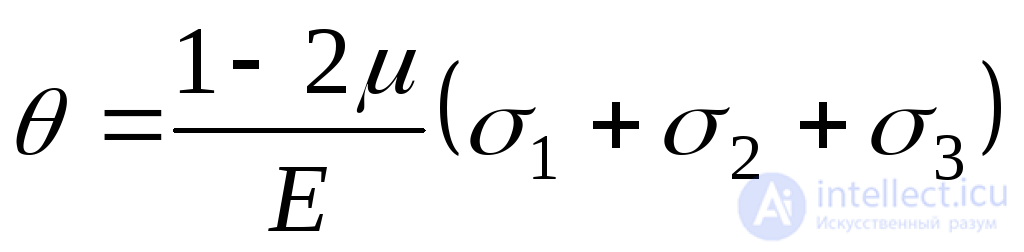. (9.82)

В частности, при равномерном всестороннем сжатии, когда

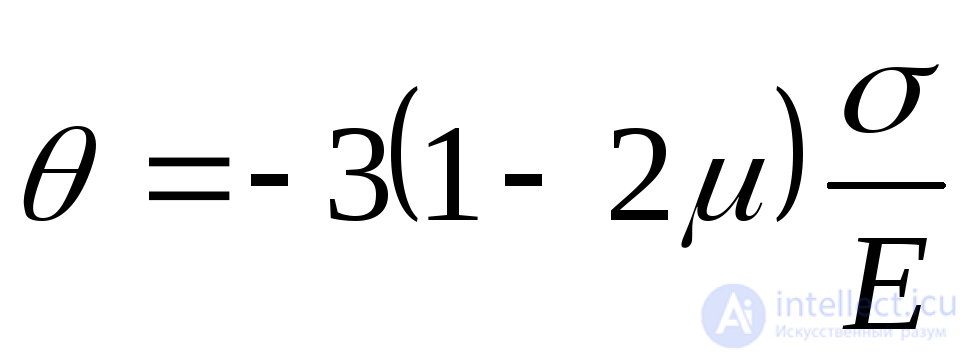. (9.83)

Из выражения (9.83) следует, что коэффициент Пуассона не может быть больше 0,5, так как в противном случае при всестороннем сжатии тело будет не уменьшаться, а увеличиваться в объеме, что противоречит физическому смыслу. Этот вывод подтверждается опытными данными. В природе не обнаружено материалов, у которых коэффициент Пуассона был бы больше 0,5.

Существуют материалы (например, парафин), у которых коэффициент Пуассона приближается к величине 0,5. В этом случае, при всестороннем сжатии не будет происходить изменения объема. Таким образом, парафин по своим упругим свойствам приближается к несжимаемой жидкости.

Для пластической стали, находящейся в состоянии текучести, коэффициент Пуассона также близок к 0,5. В связи с этим объем образца из пластической стали во время текучести не меняется.

Вычислим теперь среднее напряжение (Рис.9.26,б):

.

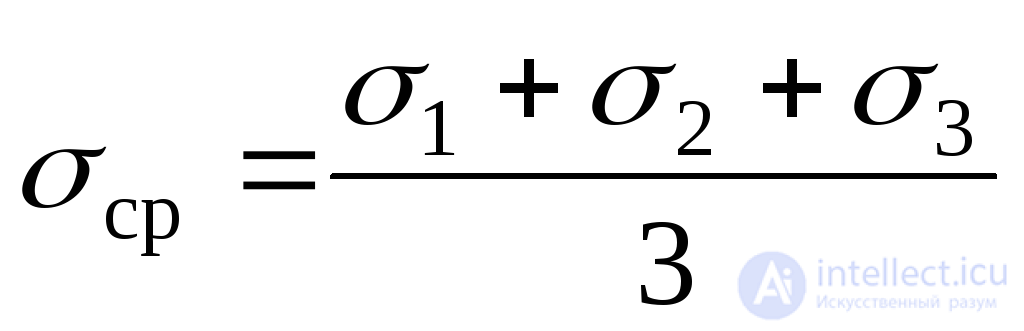Подставляя среднее напряжение в формулу (9.82), получим:

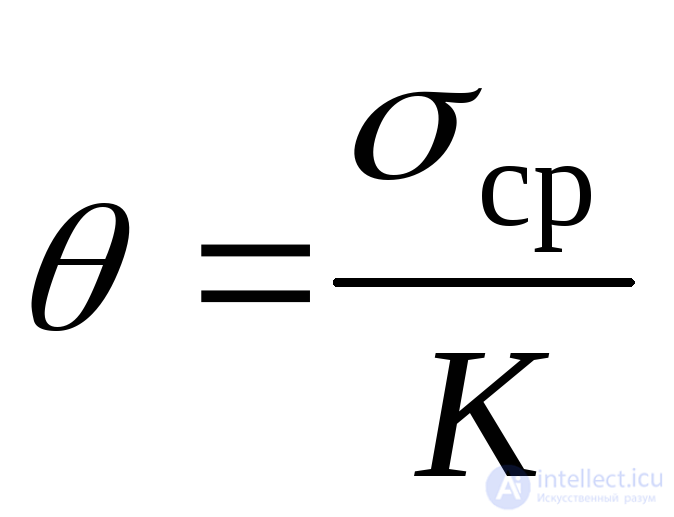, (9.84)

где

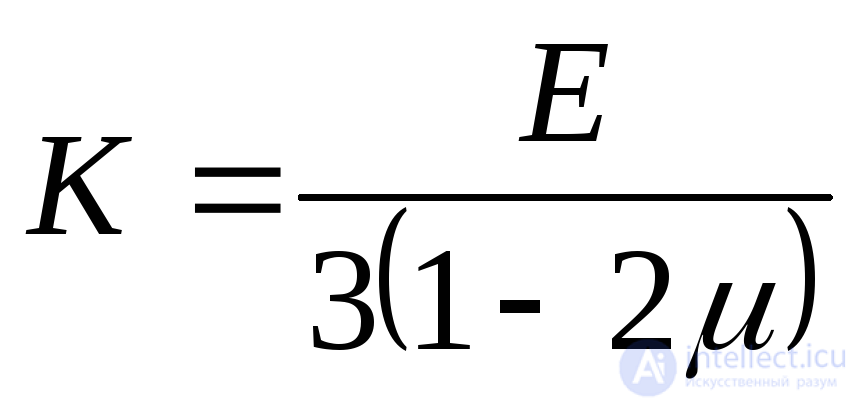. (9.85)

Величина называется модулем объемной деформации, а выражение (9.84) –объемным законом Гука. В соответствии с этим закономотносительное изменение объема пропорционально среднему напряжению.

Напряжения в площадкае, произвольно наклоненной к главным осям

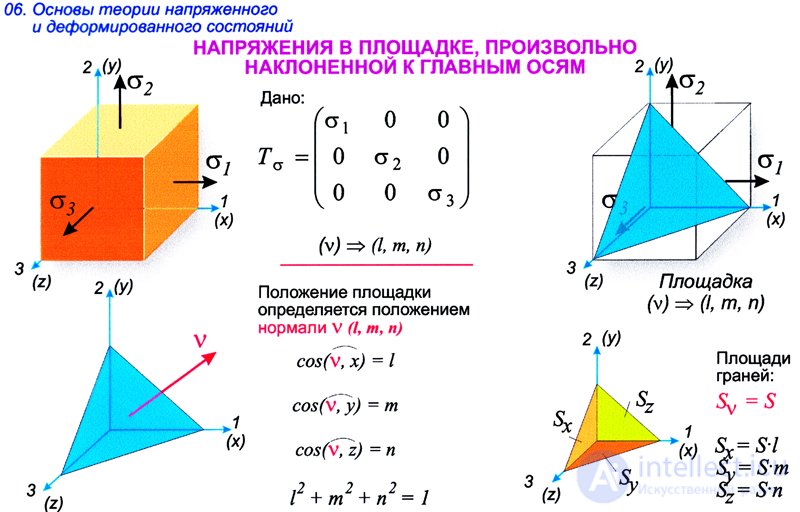
Напряжения в октаэдрических площадках

Напряжения в площадках, параллельных главным осям

Круг напряжений О.Мора

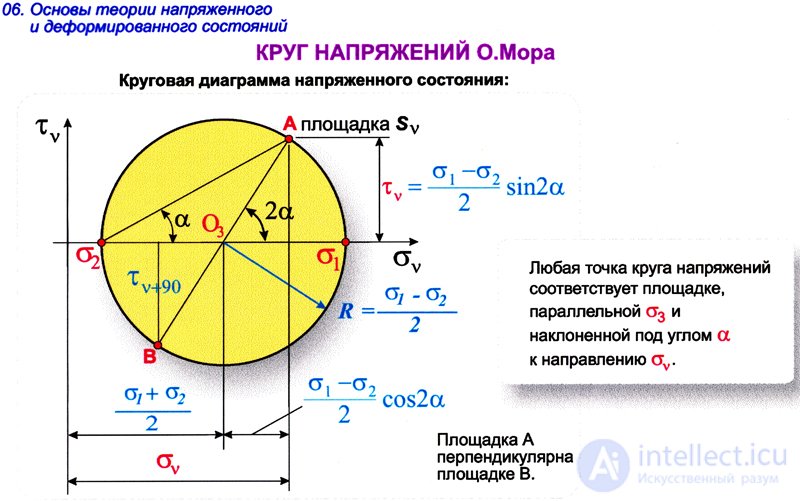
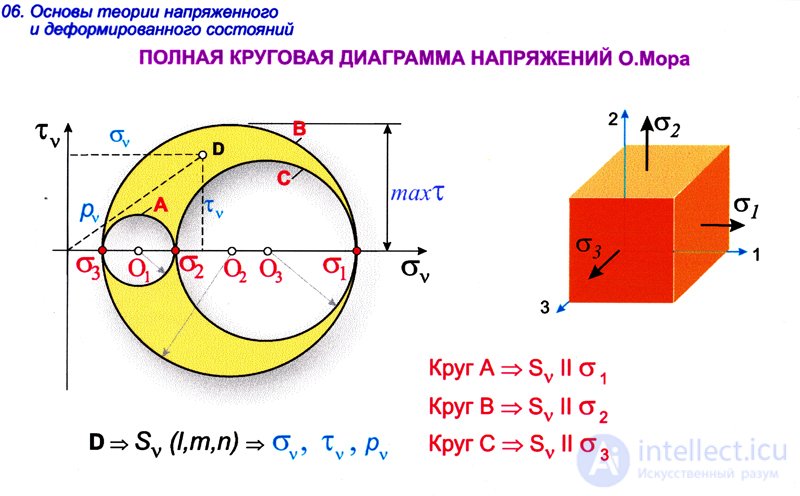
Определение главных осей и главных напряжений

Для наглядного анализа деформированного состояния в точке часто используются круги Мора, которые позволяют визуализировать напряжения и деформации в разных направлениях. Эти круги помогают определить главные напряжения и углы наклона главных осей.

Области применения деформированного состояния в точке

Области применения деформированного состояния в точке и сопротивления материалов охватывают широкий спектр инженерных и научных дисциплин. Вот некоторые ключевые области, где эти принципы находят свое применение:

1. Гражданское строительство:

   • Проектирование и анализ зданий, мостов, дорог, дамб и других инфраструктурных объектов.

   • Оценка устойчивости и долговечности конструкций под воздействием различных нагрузок, таких как ветер, землетрясения и транспорт.

2. Механическая инженерия:

   • Проектирование и анализ машин, механизмов и оборудования, включая автомобили, самолеты и промышленные станки.

   • Оптимизация компонентов для повышения их надежности и эффективности.

3. Аэрокосмическая инженерия:

   • Разработка и анализ конструкций космических аппаратов и самолетов.

   • Оценка прочности материалов в условиях экстремальных температур и динамических нагрузок.

4. Автомобильная промышленность:

   • Проектирование и тестирование автокомпонентов, таких как шасси, кузов и двигатели.

   • Анализ ударопрочности и безопасного поведения автомобилей при авариях.

5. Энергетика:

   • Проектирование и анализ трубопроводов, резервуаров и других сооружений для транспортировки и хранения нефти, газа и других энергетических ресурсов.

   • Оценка влияния давления и температуры на материалы в энергетических установках.

6. Производство и материалы:

   • Разработка новых материалов и анализ их поведения под нагрузкой.

   • Оптимизация производственных процессов для обеспечения качества и надежности продукции.

7. Биомедицинская инженерия:

   • Проектирование и анализ медицинских устройств, имплантов и протезов.

   • Изучение биомеханики тканей и органов для разработки эффективных решений в медицине.

8. Геотехническая инженерия:

   • Анализ стабильности и прочности грунтовых массивов и подземных конструкций.

   • Проектирование фундаментов и земляных сооружений.

Эти области применения показывают, насколько важными являются принципы сопротивления материалов и деформированного состояния в точке для обеспечения безопасности, надежности и эффективности различных инженерных решений.

Анализ данных, представленных в статье про деформированное состояние в точке, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое деформированное состояние в точке и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов