Лекция
Привет, Вы узнаете о том , что такое электромагнитная индукция, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электромагнитная индукция , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.
Явление электромагнитной индукции было открыто в 1831 г. М. Фарадеем (рис. 8.1) и Дж. Генри (рис. 8.2). Суть этого явления лежит в симметрии между электрическими и магнитными взаимодействиями. Если через виток, помещенный вмагнитное поле, пропускать ток, то на виток начинает действовать момент сил, поворачивающий его. Что будет, если поворачивать виток в магнитном поле? Не возникнет ли при этом электрический ток? Как мы увидим, дело обстоит именно так. На этой основе работают все генераторы переменного тока, снабжающие нас электроэнергией.

Рис. 8.1. Майкл Фарадей (1791–1867) — английский физик и химик

Рис. 8.2. Д. Генри (1797–1878) — американский физик
Познакомимся с опытами, которые проводил Фарадей (рис. 8.3, 8.4).
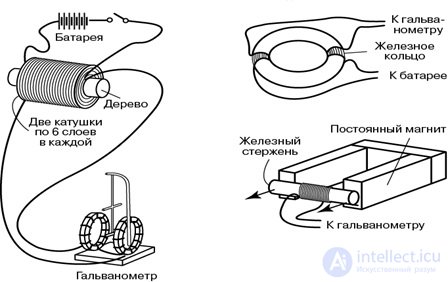
Рис. 8.3. Опыты Фарадея
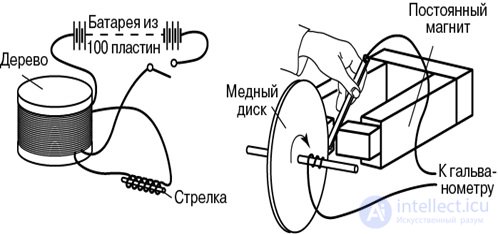
Рис. 8.4. Опыты Фарадея
Для более близкого знакомства с явлением электромагнитной индукции, подробно рассмотрим два опыта (рис. 8.5).
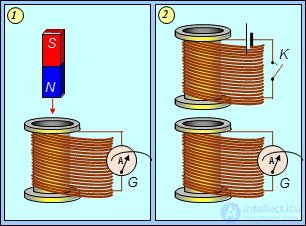
Рис. 8.5. ЭДС индукции возникает в катушке, когда:
1 — к нейприближается постоянный магнит; 2 — когда меняется ток в соседней катушке
На левом рисунке изображена катушка, подсоединенная к гальванометру G. Если приближать к витку постоянный магнит, стрелка гальванометра отклонится: по катушке пройдет ток. При неподвижном же магните ничего не происходит. На правом рисунке вблизи такой же катушки с гальванометром помещена другая катушка. Если замкнуть ключ К, то по верхней катушке пойдет электрический ток. В этот момент стрелка гальванометра отклонится, зарегистрировав импульс тока в нижней катушке. То же самое произойдет при размыкании ключа К.
см. катушек Гельмгольца.
В обоих случаях виток с гальванометром не был подсоединен к источнику тока. Тем не менее, ток в нем появился, что свидетельствует о возникновении какой-то электродвижущей силы. Ее называют ЭДС электромагнитной индукции. Рассмотренные опыты приводят к выводу, что ЭДС индукции возникает, когда что-то меняетсяв системе проводников.
Обратимся к одному из возможных вариантов изменений в системе — перемещению одного из ее проводников. Поскольку на проводник с током действует сила, то при перемещении этого проводника будет совершаться работа. Рассмотрим устройство на рис. 8.6.
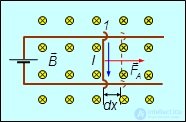
Рис. 8.6. Работа по перемещению проводника с током в магнитном поле
К рисунку 8.6: возникновение индукционного тока при движении небольшого участка замкнутого проводящего контура в магнитном поле.
Пусть отрезок проводника с током 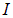 длиной
длиной 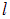 перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле
перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле
|
|
(8.1) |
Работа, совершаемая полем по перемещению проводника на расстояние 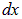 , равна
, равна
|
|
(8.2) |
Произведение 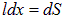 есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,
есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,
|
|
(8.3) |
где 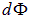 — изменение потока вектора магнитной индукции через площадь, охватываемую током.
— изменение потока вектора магнитной индукции через площадь, охватываемую током.
Согласно (8.3) работа, совершаемая магнитным полем при перемещении в нем подвижного проводника с током, равна произведению силы тока I в проводнике и потока 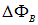 сквозь поверхность, заметаемую проводником при его движении.
сквозь поверхность, заметаемую проводником при его движении.
Полученному результату можно дать несколько иную интерпретацию. Токи, текущие в проводнике, так или иначе замкнуты, образуют контур. Если перемещать или деформировать контур с током во внешнем магнитном поле, то полная работа определится суммированием (интегрированием) элементарных работ
|
|
(8.4) |
где 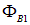 и
и 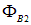 — значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).
— значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).
Пример 1. По кольцу радиусом 10 см, сделанному из тонкого гибкого провода, течет ток 100 А. Перпендикулярно плоскости кольца создано внешнее однородное магнитное поле 0,1 Тл. Направление этого поля совпадает с направлением собственного магнитного поля кругового тока на его оси. Определить работу А внешних сил, которую надо затратить, чтобы превратить кольцо в квадрат, не меняя его ориентации относительно внешнего поля. Работой против упругих сил пренебречь. Ток в кольце поддерживается постоянным. Как изменится результат, если внешнее поле будет иметь противоположное направление?
Решение. 1-й способ. Площадь кольца равна 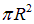 , так что поток магнитной индукции через кольцо равен
, так что поток магнитной индукции через кольцо равен 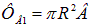 . При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца
. При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца

Его площадь равна
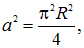
а магнитный поток
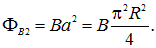
Поэтому величина работыбудет равна
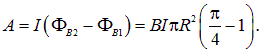
Подставляем численные значения и получаем
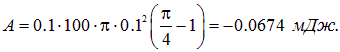
Работа получилась отрицательной, то есть ее надо совершить против сил поля. Действительно, при правовинтовом (по условию) расположении тока и внешнего поля сила Ампера стремится растянуть кольцо- увеличить его площадь. Превращая кольцо в квадрат, мы уменьшаем площадь, тем самым совершаем работу против сил поля.
Если поле имеет обратный знак, то эту работу совершит сила Ампера, и она будет положительной. При решении задачи в этом случаепотоквнешнего поля отрицателен (внешнее поле изменило свое направление на противоположное, а нормаль к поверхности, ограниченной контуром, осталась прежней, связанной правилом правого винта с направлением тока в контуре). Поэтому
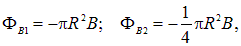
и для работы 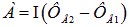 получится то же выражение, но с обратным знаком.
получится то же выражение, но с обратным знаком.
Решение. 2-й способ. Как известно, магнитный момент витка с током равен 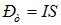 , а его потенциальная энергия в магнитном поле определяется выражением
, а его потенциальная энергия в магнитном поле определяется выражением
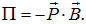
При правовинтовом расположении тока и магнитного поля угол между векторами Рm и В равен нулю, так что
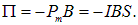
Разность потенциальных энергий при деформации витка равна
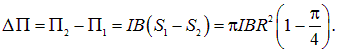
Поскольку 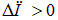 , потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен
, потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен 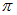 , так что
, так что
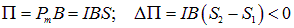
и
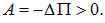
Естественно, мы получили те же результаты, что и при первом способе решения.
Пример 2. Круглый виток с током 20 А свободно установился в однородном магнитном поле с магнитной индукцией 0,016 Тл. Радиус витка равен 5 см. Определить работу, которую надо совершить, чтобы повернуть виток на углы 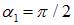 ,
, 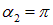 ,
, 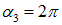 относительно оси, совпадающей с диаметром витка.
относительно оси, совпадающей с диаметром витка.
Решение. Раз в начальном положении виток установился свободно, значит его магнитный момент параллелен вектору В. Поток через плоскость витка положителен и равен 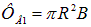 . При повороте витка на угол
. При повороте витка на угол 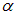 поток станет равным
поток станет равным 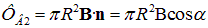 . Совершаемая при этом работабудет равна
. Совершаемая при этом работабудет равна
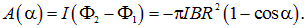
Отсюда находим
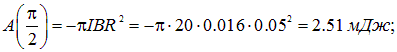
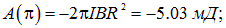
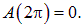
При углах поворота 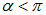 работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при
работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при 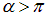 контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте
контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте 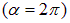 работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.
работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.
Этот пример также можно решить другим способом — в терминах потенциальной энергии взаимодействия магнитного момента с полем.
Отметим, что использовать для вычисления работы магнитный момент контура с током можно лишь в том случае, если внешнее поле однородно или слабо неоднородно. Последнее означает, что внешнее поле в пределах контура меняется настолько мало, что этим можно пренебречь. Если внешнее поле в пределах контура меняется существенно, то точный результат для работы может быть получен только путем интегрирования работы сила Ампера с учетом величины и направления внешнего поля в точке ее приложения. Такой подход и приводит к точной формуле (8.4), полученной выше на примере системы простейшей геометрии, изображенной нa рис. 8.2. Таким образом, формула (8.4) точная и общая — для задачи любой геометрии.
Применим теперь к рассмотренной системе закон сохранения энергии. Пусть 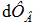 — изменение магнитного потока при небольшом перемещении проводника за время
— изменение магнитного потока при небольшом перемещении проводника за время 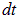 . Совершенная работа равна
. Совершенная работа равна 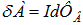 . За счет какого источника совершается эта работа? В окружающем пространстве ничего не изменилось. Единственная доступная энергия черпается из источника тока. Если его ЭДС равна
. За счет какого источника совершается эта работа? В окружающем пространстве ничего не изменилось. Единственная доступная энергия черпается из источника тока. Если его ЭДС равна 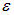 то за время
то за время 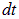 источник израсходует энергию
источник израсходует энергию 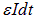 . Эта энергия тратится на выделение тепла на сопротивлении R и на работу по перемещению проводника
. Эта энергия тратится на выделение тепла на сопротивлении R и на работу по перемещению проводника
|
|
(8.5) |
Разделив обе части на 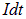 и перенося слагаемое с потоком в левую часть равенства, получаем
и перенося слагаемое с потоком в левую часть равенства, получаем
|
|
(8.6) |
В этом уравнении нетрудно узнать закон Ома: в правой части стоит падение напряжения на сопротивлении, а в левой должна стоять сумма всех действующих в цепи ЭДС. Поэтому уравнение можно переписать в виде
|
|
(8.7) |
где
|
|
(8.8) |
Это соотношение есть математическая запись закона электромагнитной индукции Фарадея (рис. 8.7).
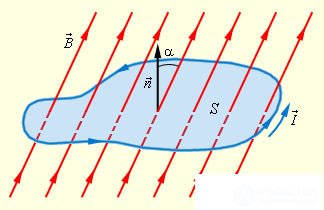
Рис. 8.7. Магнитный поток через замкнутый контур
В чем же физическая причина возникновения ЭДС индукции в данном случае? Рассмотрим почти такую же систему, но без источника тока и без замкнутой цепи. Пусть отрезок проводника длиной l движется со скоростью v перпендикулярно вектору магнитной индукции В (рис. 8.8).
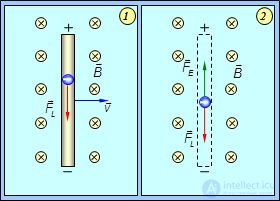
Рис. 8.8. Возникновение на концах проводника, движущегося в магнитном поле,
разности потенциалов, равной ЭДС электромагнитной индукции
Магнитное поле однородно и линии магнитной индукции 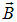 перпендикулярны чертежу и направлены от нас. На свободные электроны в проводнике действует сила Лоренца (направление которой определяется правилом буравчика)
перпендикулярны чертежу и направлены от нас. На свободные электроны в проводнике действует сила Лоренца (направление которой определяется правилом буравчика)
|
|
(8.9) |
где е — заряд электрона. Под влиянием силы Лоренца произойдет перемещение зарядов и на концах проводника возникнет некоторая разность потенциалов 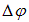 . Возникшее электрическое поле Е будет препятствовать передвижению зарядов, и их дальнейшее движение прекратится, когда сила со стороны индуцированного электрического поля
. Возникшее электрическое поле Е будет препятствовать передвижению зарядов, и их дальнейшее движение прекратится, когда сила со стороны индуцированного электрического поля 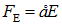 будет равна по величине, но противоположна по направлению силе Лоренца
будет равна по величине, но противоположна по направлению силе Лоренца 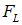 .
.
Таким образом, получаем
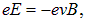
откуда
|
|
(8.10) |
Так как 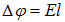 , то
, то
|
|
(8.11) |
Скорость проводника равна 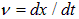 , а произведение
, а произведение 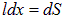 есть площадь поверхности, заметаемая проводником за время
есть площадь поверхности, заметаемая проводником за время 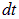 . Получаем, следовательно,
. Получаем, следовательно,
|
|
(8.12) |
Мы пришли к тому же результату, так как разность потенциалов на концах разомкнутого проводника равняется ЭДС индукции. (Напомним, что и для обычного источника тока разность потенциалов на его клеммах при разомкнутой цепи равна ЭДС.) Поскольку сила Лоренца, действующая на отрицательно заряженные электроны, направлена на рис. 8.3 вниз, на нижнем конце проводника скапливается избыток отрицательного заряда, а на верхнем — положительного. Следовательно, потенциал верхнего конца выше потенциала нижнего. Впрочем, о знаке ЭДС индукции мы поговорим особо.
Напомним, что ранее мы рассмотрели пример (п. 6.7), в котором речь шла о самолете, летящем в вертикальном магнитном поле. Нетрудно заметить, что проблема в том примере идентична только что рассмотренной задаче о движении проводника. И из преобразований Лоренца мы получили тогда в точности те же результаты, что и сейчас: сравните формулы (8.10) и (6.43). Таким образом, и закон сохранения энергии, и уравнение динамики заряда в магнитном поле, и даже релятивистские преобразования Лоренца для электромагнитного поля приводят к тому же закону Фарадея — в физике (как и вообще в мире) все взаимосвязано.
Выражение (8.8) для ЭДС электромагнитной индукции имеет очень общий вид: в него не вошли никакие конкретные характеристики движения: скорость проводника, его длина и т. п. Все определяется только скоростью изменения потока вектора магнитной индукции. При этом совершенно неважно, каким путем мы изменяем этот поток. Можно деформировать виток, перемещать его или просто увеличивать магнитную индукцию (рис 8.9, 8.10, 8.11, 8.12, 8.13). Именно последний вариант реализовался в опытах, которые мы обсуждали в начале этой главы. Механизм возникновения ЭДС индукции может бытьразным, но конечный результат будет описываться тем же уравнением (8.8), которое носит название закона Фарадея.
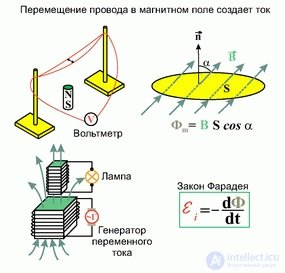
Рис. 8.9. Закон Фарадея
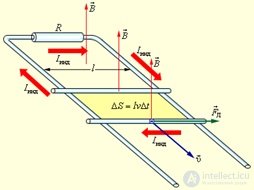
Рис. 8.10. Возникновение тока в контуре при перемещении провода в постоянном магнитном поле
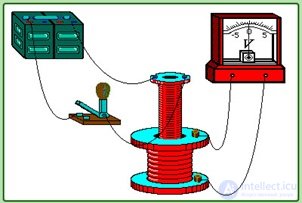
Рис. 8.11. Возникновение тока в контуре при подключении батареи
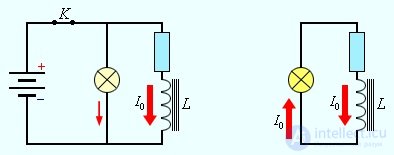
Рис. 8.12. Яркое вспыхивание лампочки при размыкании ключа
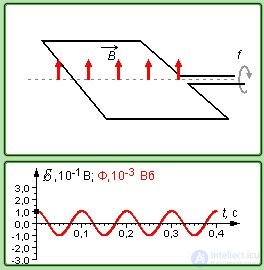
Рис. 8.13. Возникновение переменного тока при вращении контура
Пример 1. В однородном магнитном поле с индукцией 0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной 10 см. Ось вращения проходит через один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения 16 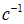 .
.
Решение. За время 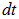 стержень повернется на угол
стержень повернется на угол 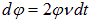 и заметет сектор площадью
и заметет сектор площадью
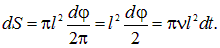
Разность потенциалов равна скорости изменения потока магнитной индукции
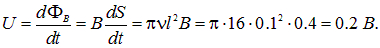
Закон Фарадея применим не только к отдельному контуру или витку, но и к катушке, которую можно рассматривать как N витков, соединенных последовательно. В этом случае суммарная ЭДС будет в N раз больше, чем ЭДС отдельного витка, то есть
|
|
(8.13) |
где величина
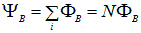
называется потокосцеплением или полным магнитным потоком (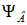 измеряется в тех же единицах, что и
измеряется в тех же единицах, что и 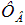 , то есть в веберах).
, то есть в веберах).
Пример 2. Магнитная индукция поля между полюсами магнита генератора равна 0,8 Тл. Об этом говорит сайт https://intellect.icu . Ротор имеет 100 витков площадью 400 см2. Определить частоту вращения якоря, если максимальная ЭДС индукции равна 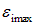 = 200 В (рис. 8.14).
= 200 В (рис. 8.14).
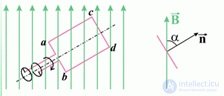
Рис. 8.14. Вращение контура в постоянном магнитном поле
Решение. Угол между магнитным полем и нормалью к плоскости витков изменяется по закону 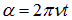 . Полный магнитный поток через обмотку ротора в момент времени t равен
. Полный магнитный поток через обмотку ротора в момент времени t равен 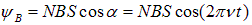 . Дифференцируямагнитный поток по времени, получаем
. Дифференцируямагнитный поток по времени, получаем
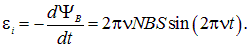
Максимальное значение синуса равно единице, следовательно, максимальное значение ЭДС индукции равно
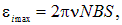
откуда
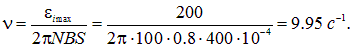
ЭДС индукции возникает не только при перемещении замкнутого контура в магнитном поле или перемещении магнита относительно неподвижного контура. Пусть имеются две катушки с общим железным сердечником, служащим в качестве магнитопровода (рис. 8.15).
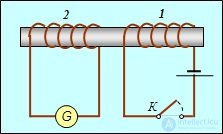
Рис. 8.15. Железный сердечник как магнитопровод между двумя катушками
При разомкнутой цепи магнитный поток в системе равен нулю. При замыкании ключа К через катушку 1 пойдет ток, который создаст магнитное поле, так что катушка 2 будет пронизываться магнитным потоком 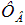 . Поэтому при замыкании ключа за время
. Поэтому при замыкании ключа за время 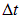 нарастания тока до стационарного значения поток через катушку 2, меняется на величину
нарастания тока до стационарного значения поток через катушку 2, меняется на величину 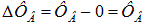 . Соответственно, в ней возникает ЭДС
. Соответственно, в ней возникает ЭДС
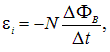
где N — число витков в катушке 2, и идет индукционный ток, который зарегистрирует гальванометр G.
Когда возрастание тока в катушке 1 прекратится, поток магнитной индукции станет постоянным и ЭДС будет равна нулю. Ток в катушке 2 также перестанет идти, и стрелка гальванометра вернется в исходное положение. Такая же картина будет наблюдаться и при размыкании цепи катушки 1, только стрелка гальванометра отклонится в другую сторону, что свидетельствует об изменении направления тока в катушке 2.
Если через катушку 1 пропустить переменный ток, то по цепи катушки 2 пойдет переменный ток той же частоты. Этот принцип широко используется в трансформаторной технике.
Пусть контур имеет сопротивление R и пусть магнитный поток через него меняется по какому-то закону. Возникающая в контуре ЭДС электромагнитной индукции
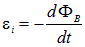
вызывает в контуре ток
|
|
(8.14) |
Заряд 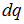 , протекший в контуре за время
, протекший в контуре за время 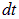 , связан с током
, связан с током
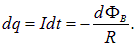
Интегрируя, получаем для заряда Q, протекшего по контуру при изменении потока следующее выражение
|
|
(8.15) |
(мы используем модуль изменения потока, так как направление перетекания заряда нам сейчас не важно). Отсюда, кстати, вытекает связь единицы измерения магнитного потока с зарядом и сопротивлением
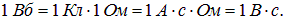
Пример 3. Проволочное кольцо радиусом 10 см лежит на столе. Какой заряд протечет по кольцу, если его повернуть с одной стороны на другую. Сопротивление кольца 3 Ом.
продолжение следует...
Часть 1 8. Электромагнитная индукция
Часть 2 8.3. Явление самоиндукции - 8. Электромагнитная индукция
Часть 3 8.5. Коэффициенты взаимной индукции системы контуров с током - 8.
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика