Лекция
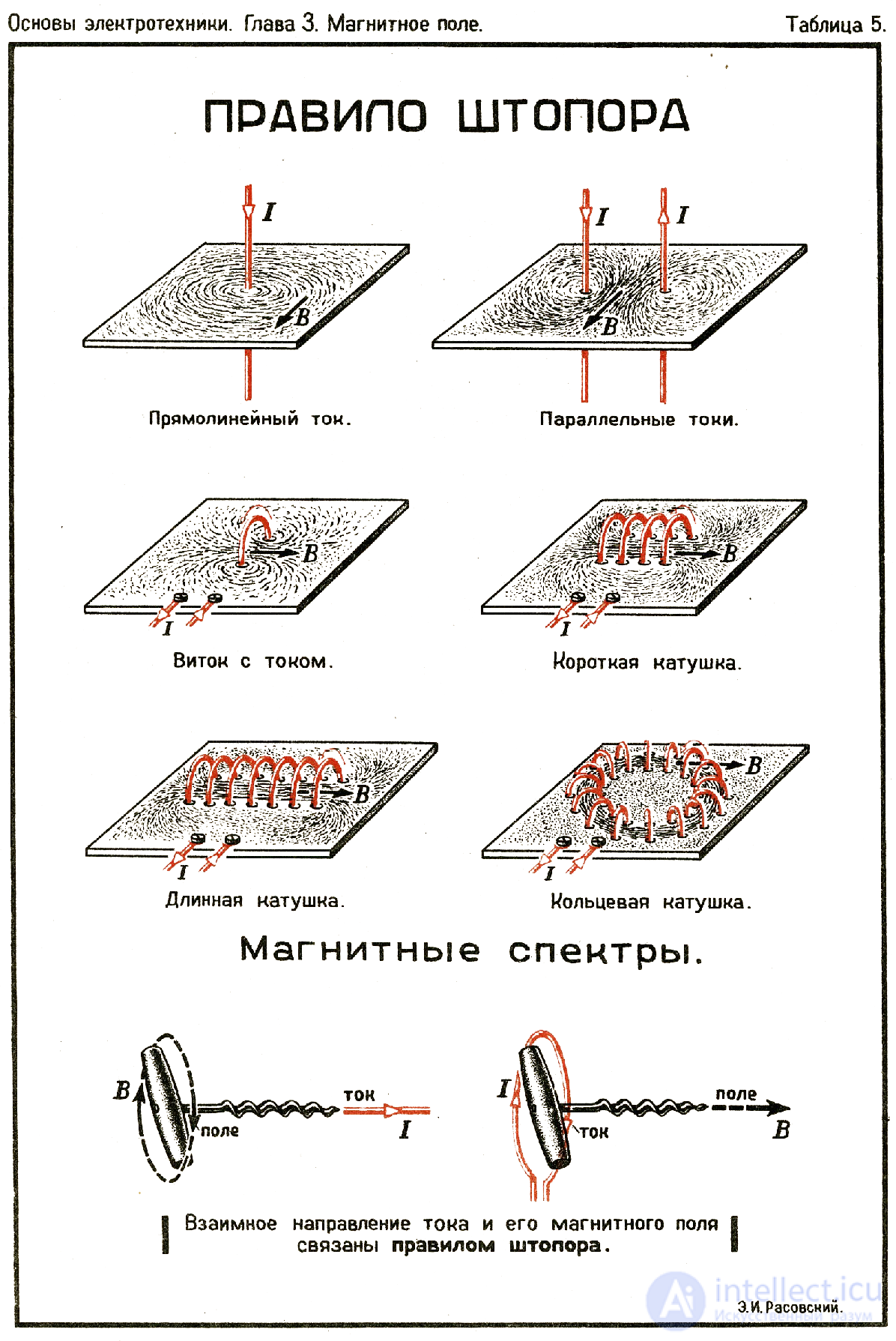
Привет, Вы узнаете о том , что такое электромагнитная индукция, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электромагнитная индукция, правило левой руки, правило буравчика, правило штопора, правило правой руки, самоиндукция, взаимоиндукция , настоятельно рекомендую прочитать все из категории Базовая физика.
Явление электромагнитной индукции было открыто в 1831 г. М. Фарадеем (рис. 8.1) и Дж. Генри (рис. 8.2). Суть этого явления лежит в симметрии между электрическими и магнитными взаимодействиями. Если через виток, помещенный вмагнитное поле, пропускать ток, то на виток начинает действовать момент сил, поворачивающий его. Что будет, если поворачивать виток в магнитном поле? Не возникнет ли при этом электрический ток? Как мы увидим, дело обстоит именно так. На этой основе работают все генераторы переменного тока, снабжающие нас электроэнергией.

Рис. 8.1. Майкл Фарадей (1791–1867) — английский физик и химик

Рис. 8.2. Д. Генри (1797–1878) — американский физик
Познакомимся с опытами, которые проводил Фарадей (рис. 8.3, 8.4).
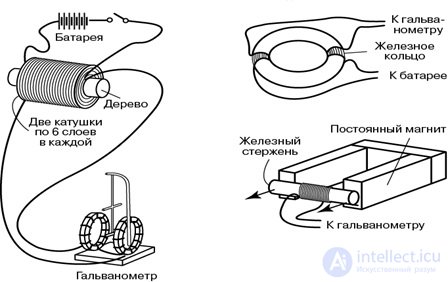
Рис. 8.3. Опыты Фарадея
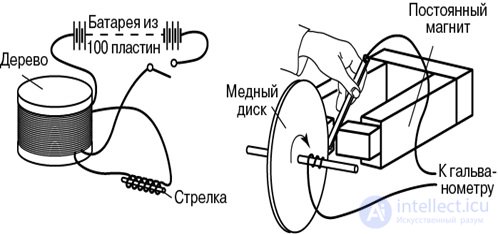
Рис. 8.4. Опыты Фарадея
Для более близкого знакомства с явлением электромагнитной индукции, подробно рассмотрим два опыта (рис. 8.5).
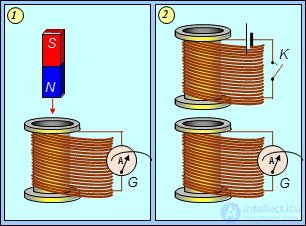
Рис. 8.5. ЭДС индукции возникает в катушке, когда:
1 — к нейприближается постоянный магнит; 2 — когда меняется ток в соседней катушке
На левом рисунке изображена катушка, подсоединенная к гальванометру G. Если приближать к витку постоянный магнит, стрелка гальванометра отклонится: по катушке пройдет ток. При неподвижном же магните ничего не происходит. На правом рисунке вблизи такой же катушки с гальванометром помещена другая катушка. Если замкнуть ключ К, то по верхней катушке пойдет электрический ток. В этот момент стрелка гальванометра отклонится, зарегистрировав импульс тока в нижней катушке. То же самое произойдет при размыкании ключа К.
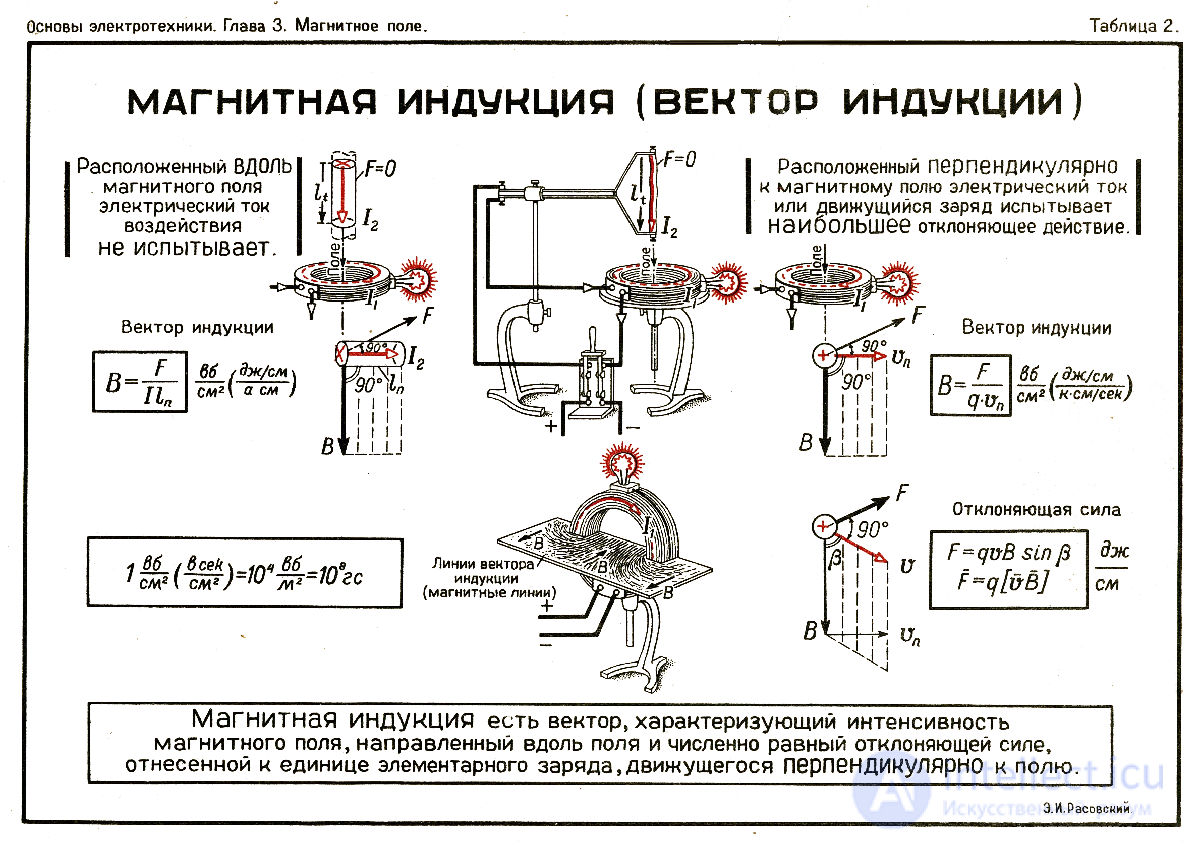
см. катушек Гельмгольца.
В обоих случаях виток с гальванометром не был подсоединен к источнику тока. Тем не менее, ток в нем появился, что свидетельствует о возникновении какой-то электродвижущей силы. Ее называют ЭДС электромагнитной индукции. Рассмотренные опыты приводят к выводу, что ЭДС индукции возникает, когда что-то меняетсяв системе проводников.
Обратимся к одному из возможных вариантов изменений в системе — перемещению одного из ее проводников. Поскольку на проводник с током действует сила, то при перемещении этого проводника будет совершаться работа. Рассмотрим устройство на рис. 8.6.
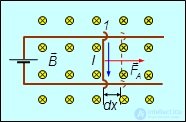
Рис. 8.6. Работа по перемещению проводника с током в магнитном поле
К рисунку 8.6: возникновение индукционного тока при движении небольшого участка замкнутого проводящего контура в магнитном поле.
Пусть отрезок проводника с током 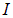 длиной
длиной 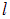 перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле
перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле
|
|
(8.1) |
Работа, совершаемая полем по перемещению проводника на расстояние 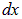 , равна
, равна
|
|
(8.2) |
Произведение 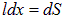 есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,
есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,
|
|
(8.3) |
где 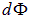 — изменение потока вектора магнитной индукции через площадь, охватываемую током.
— изменение потока вектора магнитной индукции через площадь, охватываемую током.
Согласно (8.3) работа, совершаемая магнитным полем при перемещении в нем подвижного проводника с током, равна произведению силы тока I в проводнике и потока 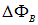 сквозь поверхность, заметаемую проводником при его движении.
сквозь поверхность, заметаемую проводником при его движении.
Полученному результату можно дать несколько иную интерпретацию. Токи, текущие в проводнике, так или иначе замкнуты, образуют контур. Если перемещать или деформировать контур с током во внешнем магнитном поле, то полная работа определится суммированием (интегрированием) элементарных работ
|
|
(8.4) |
где 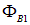 и
и 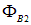 — значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).
— значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).
Пример 1. По кольцу радиусом 10 см, сделанному из тонкого гибкого провода, течет ток 100 А. Перпендикулярно плоскости кольца создано внешнее однородное магнитное поле 0,1 Тл. Направление этого поля совпадает с направлением собственного магнитного поля кругового тока на его оси. Определить работу А внешних сил, которую надо затратить, чтобы превратить кольцо в квадрат, не меняя его ориентации относительно внешнего поля. Работой против упругих сил пренебречь. Ток в кольце поддерживается постоянным. Как изменится результат, если внешнее поле будет иметь противоположное направление?
Решение. 1-й способ. Площадь кольца равна 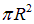 , так что поток магнитной индукции через кольцо равен
, так что поток магнитной индукции через кольцо равен 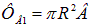 . При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца
. При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца

Его площадь равна
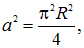
а магнитный поток
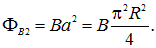
Поэтому величина работыбудет равна
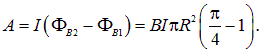
Подставляем численные значения и получаем
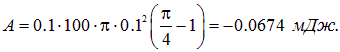
Работа получилась отрицательной, то есть ее надо совершить против сил поля. Действительно, при правовинтовом (по условию) расположении тока и внешнего поля сила Ампера стремится растянуть кольцо- увеличить его площадь. Превращая кольцо в квадрат, мы уменьшаем площадь, тем самым совершаем работу против сил поля.
Если поле имеет обратный знак, то эту работу совершит сила Ампера, и она будет положительной. При решении задачи в этом случаепотоквнешнего поля отрицателен (внешнее поле изменило свое направление на противоположное, а нормаль к поверхности, ограниченной контуром, осталась прежней, связанной правилом правого винта с направлением тока в контуре). Поэтому
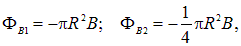
и для работы 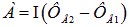 получится то же выражение, но с обратным знаком.
получится то же выражение, но с обратным знаком.
Решение. 2-й способ. Как известно, магнитный момент витка с током равен 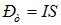 , а его потенциальная энергия в магнитном поле определяется выражением
, а его потенциальная энергия в магнитном поле определяется выражением
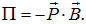
При правовинтовом расположении тока и магнитного поля угол между векторами Рm и В равен нулю, так что
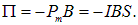
Разность потенциальных энергий при деформации витка равна
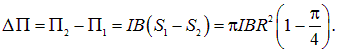
Поскольку 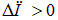 , потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен
, потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен 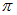 , так что
, так что
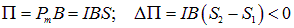
и
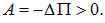
Естественно, мы получили те же результаты, что и при первом способе решения.
Пример 2. Круглый виток с током 20 А свободно установился в однородном магнитном поле с магнитной индукцией 0,016 Тл. Радиус витка равен 5 см. Определить работу, которую надо совершить, чтобы повернуть виток на углы 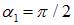 ,
, 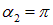 ,
, 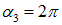 относительно оси, совпадающей с диаметром витка.
относительно оси, совпадающей с диаметром витка.
Решение. Раз в начальном положении виток установился свободно, значит его магнитный момент параллелен вектору В. Поток через плоскость витка положителен и равен 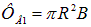 . При повороте витка на угол
. При повороте витка на угол 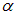 поток станет равным
поток станет равным 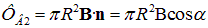 . Совершаемая при этом работабудет равна
. Совершаемая при этом работабудет равна
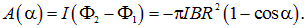
Отсюда находим
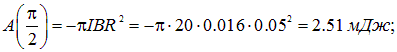
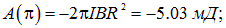
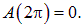
При углах поворота 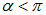 работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при
работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при 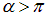 контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте
контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте 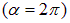 работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.
работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.
Этот пример также можно решить другим способом — в терминах потенциальной энергии взаимодействия магнитного момента с полем.
Отметим, что использовать для вычисления работы магнитный момент контура с током можно лишь в том случае, если внешнее поле однородно или слабо неоднородно. Последнее означает, что внешнее поле в пределах контура меняется настолько мало, что этим можно пренебречь. Если внешнее поле в пределах контура меняется существенно, то точный результат для работы может быть получен только путем интегрирования работы сила Ампера с учетом величины и направления внешнего поля в точке ее приложения. Такой подход и приводит к точной формуле (8.4), полученной выше на примере системы простейшей геометрии, изображенной нa рис. 8.2. Таким образом, формула (8.4) точная и общая — для задачи любой геометрии.
Применим теперь к рассмотренной системе закон сохранения энергии. Пусть 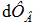 — изменение магнитного потока при небольшом перемещении проводника за время
— изменение магнитного потока при небольшом перемещении проводника за время 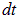 . Совершенная работа равна
. Совершенная работа равна 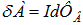 . За счет какого источника совершается эта работа? В окружающем пространстве ничего не изменилось. Единственная доступная энергия черпается из источника тока. Если его ЭДС равна
. За счет какого источника совершается эта работа? В окружающем пространстве ничего не изменилось. Единственная доступная энергия черпается из источника тока. Если его ЭДС равна 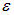 то за время
то за время 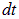 источник израсходует энергию
источник израсходует энергию 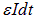 . Эта энергия тратится на выделение тепла на сопротивлении R и на работу по перемещению проводника
. Эта энергия тратится на выделение тепла на сопротивлении R и на работу по перемещению проводника
|
|
(8.5) |
Разделив обе части на 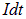 и перенося слагаемое с потоком в левую часть равенства, получаем
и перенося слагаемое с потоком в левую часть равенства, получаем
|
|
(8.6) |
В этом уравнении нетрудно узнать закон Ома: в правой части стоит падение напряжения на сопротивлении, а в левой должна стоять сумма всех действующих в цепи ЭДС. Поэтому уравнение можно переписать в виде
|
|
(8.7) |
где
|
|
(8.8) |
Это соотношение есть математическая запись закона электромагнитной индукции Фарадея (рис. 8.7).
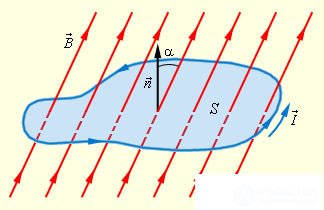
Рис. 8.7. Магнитный поток через замкнутый контур
В чем же физическая причина возникновения ЭДС индукции в данном случае? Рассмотрим почти такую же систему, но без источника тока и без замкнутой цепи. Пусть отрезок проводника длиной l движется со скоростью v перпендикулярно вектору магнитной индукции В (рис. 8.8).
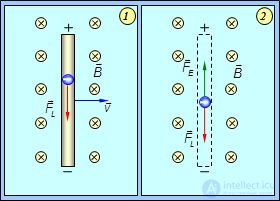
Рис. 8.8. Возникновение на концах проводника, движущегося в магнитном поле,
разности потенциалов, равной ЭДС электромагнитной индукции
Магнитное поле однородно и линии магнитной индукции 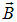 перпендикулярны чертежу и направлены от нас. На свободные электроны в проводнике действует сила Лоренца (направление которой определяется правилом буравчика)
перпендикулярны чертежу и направлены от нас. На свободные электроны в проводнике действует сила Лоренца (направление которой определяется правилом буравчика)
|
|
(8.9) |
где е — заряд электрона. Под влиянием силы Лоренца произойдет перемещение зарядов и на концах проводника возникнет некоторая разность потенциалов 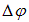 . Возникшее электрическое поле Е будет препятствовать передвижению зарядов, и их дальнейшее движение прекратится, когда сила со стороны индуцированного электрического поля
. Возникшее электрическое поле Е будет препятствовать передвижению зарядов, и их дальнейшее движение прекратится, когда сила со стороны индуцированного электрического поля 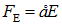 будет равна по величине, но противоположна по направлению силе Лоренца
будет равна по величине, но противоположна по направлению силе Лоренца 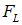 .
.
Таким образом, получаем
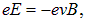
откуда
|
|
(8.10) |
Так как 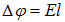 , то
, то
|
|
(8.11) |
Скорость проводника равна 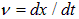 , а произведение
, а произведение 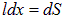 есть площадь поверхности, заметаемая проводником за время
есть площадь поверхности, заметаемая проводником за время 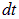 . Получаем, следовательно,
. Получаем, следовательно,
|
|
(8.12) |
Мы пришли к тому же результату, так как разность потенциалов на концах разомкнутого проводника равняется ЭДС индукции. (Напомним, что и для обычного источника тока разность потенциалов на его клеммах при разомкнутой цепи равна ЭДС.) Поскольку сила Лоренца, действующая на отрицательно заряженные электроны, направлена на рис. 8.3 вниз, на нижнем конце проводника скапливается избыток отрицательного заряда, а на верхнем — положительного. Следовательно, потенциал верхнего конца выше потенциала нижнего. Впрочем, о знаке ЭДС индукции мы поговорим особо.
Напомним, что ранее мы рассмотрели пример (п. 6.7), в котором речь шла о самолете, летящем в вертикальном магнитном поле. Нетрудно заметить, что проблема в том примере идентична только что рассмотренной задаче о движении проводника. И из преобразований Лоренца мы получили тогда в точности те же результаты, что и сейчас: сравните формулы (8.10) и (6.43). Таким образом, и закон сохранения энергии, и уравнение динамики заряда в магнитном поле, и даже релятивистские преобразования Лоренца для электромагнитного поля приводят к тому же закону Фарадея — в физике (как и вообще в мире) все взаимосвязано.
Выражение (8.8) для ЭДС электромагнитной индукции имеет очень общий вид: в него не вошли никакие конкретные характеристики движения: скорость проводника, его длина и т. п. Все определяется только скоростью изменения потока вектора магнитной индукции. При этом совершенно неважно, каким путем мы изменяем этот поток. Можно деформировать виток, перемещать его или просто увеличивать магнитную индукцию (рис 8.9, 8.10, 8.11, 8.12, 8.13). Именно последний вариант реализовался в опытах, которые мы обсуждали в начале этой главы. Механизм возникновения ЭДС индукции может бытьразным, но конечный результат будет описываться тем же уравнением (8.8), которое носит название закона Фарадея.
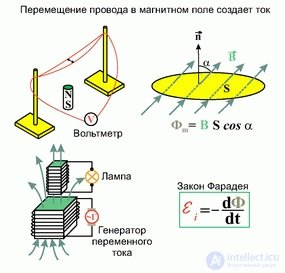
Рис. 8.9. Закон Фарадея
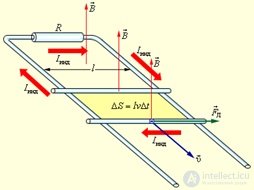
Рис. 8.10. Возникновение тока в контуре при перемещении провода в постоянном магнитном поле
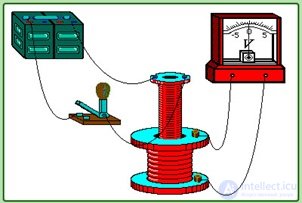
Рис. 8.11. Возникновение тока в контуре при подключении батареи
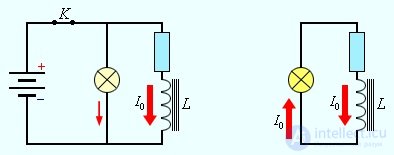
Рис. 8.12. Яркое вспыхивание лампочки при размыкании ключа
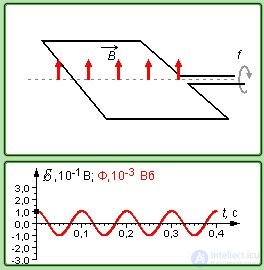
Рис. 8.13. Возникновение переменного тока при вращении контура
Пример 1. В однородном магнитном поле с индукцией 0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной 10 см. Ось вращения проходит через один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения 16 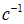 .
.
Решение. За время 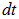 стержень повернется на угол
стержень повернется на угол 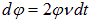 и заметет сектор площадью
и заметет сектор площадью
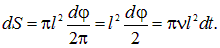
Разность потенциалов равна скорости изменения потока магнитной индукции
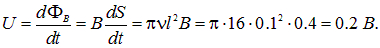
Закон Фарадея применим не только к отдельному контуру или витку, но и к катушке, которую можно рассматривать как N витков, соединенных последовательно. В этом случае суммарная ЭДС будет в N раз больше, чем ЭДС отдельного витка, то есть
|
|
(8.13) |
где величина
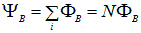
называется потокосцеплением или полным магнитным потоком (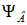 измеряется в тех же единицах, что и
измеряется в тех же единицах, что и 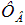 , то есть в веберах).
, то есть в веберах).
Пример 2. Магнитная индукция поля между полюсами магнита генератора равна 0,8 Тл. Ротор имеет 100 витков площадью 400 см2. Определить частоту вращения якоря, если максимальная ЭДС индукции равна 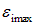 = 200 В (рис. 8.14).
= 200 В (рис. 8.14).
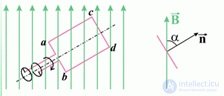
Рис. 8.14. Вращение контура в постоянном магнитном поле
Решение. Угол между магнитным полем и нормалью к плоскости витков изменяется по закону 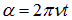 . Полный магнитный поток через обмотку ротора в момент времени t равен
. Полный магнитный поток через обмотку ротора в момент времени t равен 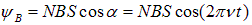 . Дифференцируямагнитный поток по времени, получаем
. Дифференцируямагнитный поток по времени, получаем
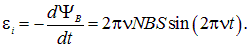
Максимальное значение синуса равно единице, следовательно, максимальное значение ЭДС индукции равно
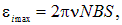
откуда
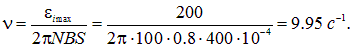
ЭДС индукции возникает не только при перемещении замкнутого контура в магнитном поле или перемещении магнита относительно неподвижного контура. Пусть имеются две катушки с общим железным сердечником, служащим в качестве магнитопровода (рис. Об этом говорит сайт https://intellect.icu . 8.15).
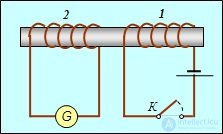
Рис. 8.15. Железный сердечник как магнитопровод между двумя катушками
При разомкнутой цепи магнитный поток в системе равен нулю. При замыкании ключа К через катушку 1 пойдет ток, который создаст магнитное поле, так что катушка 2 будет пронизываться магнитным потоком 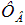 . Поэтому при замыкании ключа за время
. Поэтому при замыкании ключа за время 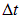 нарастания тока до стационарного значения поток через катушку 2, меняется на величину
нарастания тока до стационарного значения поток через катушку 2, меняется на величину 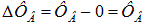 . Соответственно, в ней возникает ЭДС
. Соответственно, в ней возникает ЭДС
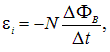
где N — число витков в катушке 2, и идет индукционный ток, который зарегистрирует гальванометр G.
Когда возрастание тока в катушке 1 прекратится, поток магнитной индукции станет постоянным и ЭДС будет равна нулю. Ток в катушке 2 также перестанет идти, и стрелка гальванометра вернется в исходное положение. Такая же картина будет наблюдаться и при размыкании цепи катушки 1, только стрелка гальванометра отклонится в другую сторону, что свидетельствует об изменении направления тока в катушке 2.
Если через катушку 1 пропустить переменный ток, то по цепи катушки 2 пойдет переменный ток той же частоты. Этот принцип широко используется в трансформаторной технике.
Пусть контур имеет сопротивление R и пусть магнитный поток через него меняется по какому-то закону. Возникающая в контуре ЭДС электромагнитной индукции
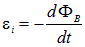
вызывает в контуре ток
|
|
(8.14) |
Заряд 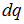 , протекший в контуре за время
, протекший в контуре за время 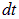 , связан с током
, связан с током
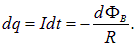
Интегрируя, получаем для заряда Q, протекшего по контуру при изменении потока следующее выражение
|
|
(8.15) |
(мы используем модуль изменения потока, так как направление перетекания заряда нам сейчас не важно). Отсюда, кстати, вытекает связь единицы измерения магнитного потока с зарядом и сопротивлением
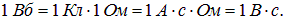
Пример 3. Проволочное кольцо радиусом 10 см лежит на столе. Какой заряд протечет по кольцу, если его повернуть с одной стороны на другую. Сопротивление кольца 3 Ом. Вертикальная составляющая индукции магнитного поля Земли равна 50 мкТл.
Решение. Начальный поток магнитной индукции через кольцо равен  . После переворачивания кольца величина потока будет той же, но силовые линии входят теперь с другой стороны кольца:
. После переворачивания кольца величина потока будет той же, но силовые линии входят теперь с другой стороны кольца:  . Искомый заряд равен
. Искомый заряд равен

В 1833 г. Э.X. Ленц (рис. 8.16) сформулировал правило (правило Ленца):

Рис. 8.16. Э.Х. Ленц (1804–1865) — русский физик
|
Индукционный ток всегда имеет такое направление, что его магнитное поле противодействует изменению магнитного потока, пронизывающего контур. |
Приведем пример использования правила Ленца (рис. 8.17, 8.18).
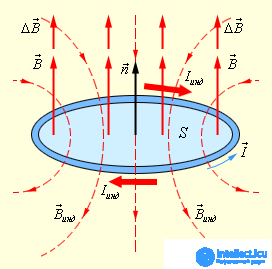
Рис. 8.17. Иллюстрация правила Ленца

Рис. 8.18. Иллюстрация правила Ленца
Рассматривая рис. 8.8, мы видели, что избыточный положительный заряд накапливался на верхнем конце проводника. Следовательно, в то короткое время, пока движение зарядов в проводнике не прекратилось, индукционный ток тек снизу вверх. По правилу буравчика (поворот ручки от направления тока к направлению поля), сила Ампера была направлена налево, препятствуя движению проводника направо.
В опыте, когда постоянный магнит приближается к витку, индуцированный ток также создает противодействующее магнитное поле (рис. 8.19).
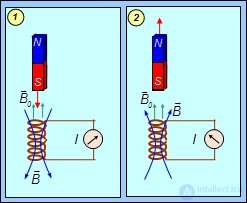
Рис. 8.19. При перемещении постоянного магнита в катушке возникает индукционный ток,
поле которого препятствует перемещению магнита
На рис. 8.20 показан опыт, иллюстрирующий правило Ленца. На концах коромысла, которое может вращаться вокруг вертикальной оси, укреплены два алюминиевых кольца: одно сплошное, а другое — с разрезом. при приближении к первому кольцу постоянного магнита оно отталкивается от него. а при удалении — притягивается, поскольку индукционные токи в соответствии с правилом Ленца препятствуют изменению магнитного потока, охватываемого кольцом. С разрезанным кольцом магнит не взаимодействует.

Рис. 8.20. Взаимодействие постоянного магнита с проводящим кольцом
На рис. 8.21 представлен опыт, в котором демонстрируется взаимодействие проводящего кольца и электромагнита. Кольцо, надетое на выступающий из обмотки конец вертикального сердечника, при включении тока в обмотке взлетает вверх. При горизонтальном расположении сердечника в соответствии с правилом Ленца при включении поля перемещается по сердечнику в сторону от обмотки, а при выключении — обратно к обмотке.

Рис. 8.21. Взаимодействие электромагнита с проводящим кольцом
Математически правило Ленца отображается знаком минус в уравнении (8.8) закона Фарадея. Обсудим подробнее эту связь. Здесь могут возникнуть трудности с определением знака потока вектора магнитной индукции. Когда мы имели дело с замкнутыми поверхностями в электростатике, положительное направление задавалось внешней нормалью. Когда незамкнутая поверхность «натянута» на контур с уже текущим током, направление тока задает положительное направление нормали по правилу буравчика. С этим мы познакомились уже при решении задач онахождении работы по деформированию контура. Но как быть в случае использования закона Фарадея, когда поверхность не замкнута, а направление тока нам не известно и мы только хотим его определить?
Рассмотрим рис. 8.22. На нем показан контур, пронизываемый силовыми линиями внешнего магнитного поля В.

Рис. 8.22. Иллюстрация применения правила Ленца:
изменение направления обхода контура не меняет знака ЭДС индукции в законе Фарадея
Выберем положительное направление обхода контура против часовой стрелки (верхний ряд). На рис. 8.22-1 магнитное поле постоянно. При данном выборе положительного направления обхода контура и остром угле между нормалью n к контуру и вектором магнитной индукции В магнитный поток через контур положителен  . На рис. 8.22-2 магнитное поле увеличивается. Положительный поток через контур также растет, и потому
. На рис. 8.22-2 магнитное поле увеличивается. Положительный поток через контур также растет, и потому  Из закона Фарадея следует тогда, что ЭДС индукции и, следовательно, индукционный ток отрицательны. Это значит, что ток течет в обратном направлении по отношению к выбранному пути обхода контура, то есть по часовой стрелке.
Из закона Фарадея следует тогда, что ЭДС индукции и, следовательно, индукционный ток отрицательны. Это значит, что ток течет в обратном направлении по отношению к выбранному пути обхода контура, то есть по часовой стрелке.
Выберем теперь иное положительное направление обхода контура — по часовой стреле (рис. 8.22-3). Поток постоянного магнитного поля здесь отрицателен (угол между n и В тупой, и его косинус отрицателен). При увеличении поля абсолютная величина потока растет, но так как он отрицателен, то ( , как показано на рис. 8.22-4). Из закона Фарадея следует тогда, что ЭДС и индукционный ток положительны. Это значит, что направление тока совпадаетс выбранным направлением обхода контура, то есть ток течет по часовой стрелке.
, как показано на рис. 8.22-4). Из закона Фарадея следует тогда, что ЭДС и индукционный ток положительны. Это значит, что направление тока совпадаетс выбранным направлением обхода контура, то есть ток течет по часовой стрелке.
Мы показали, что направление индукционного тока не зависит от выбора положительного направления обхода контура. Так и должно быть, поскольку выбор направления обхода контура делаем мы и притом произвольно, а направление тока — физическая реальность, которая не может зависеть от нашего произвола. С аналогичной ситуацией мы сталкивались при изучении правил Кирхгофа.
Индукционные токи возникают не только в проволочных витках, но и в толще массивных проводников. В этом случае их называют вихревыми токами или токами Фуко. Из–за малого сопротивления проводников они могут достигать большой силы. По правилу Ленца вихревые токи также действуют против причины, их вызывающей. На этом основана идея электромагнитных демпферов, успокаивающих колеблющиеся части приборов (стрелки гальванометров и т. п.). На подвижной части прибора укрепляется металлическая полоска, находящаяся в поле сильного магнита. При движении системы токи Ж. Фуко (рис. 8.23) тормозят ее, но они отсутствуют при покоящейся стрелке и не препятствуют ее остановке в нужном месте, согласно значению измеряемой величины (в отличие от сил трения).

Рис. 8.23. Леон Фуко (1819–1868) — французский физик и астроном
Итогом проведенных рассуждений может быть такая формулировка правила Ленца: индукционный ток всегда направлен так, чтобы препятствовать той причине, которая его породила. Вне зависимости от того, что это за причина.
Например, если проволочное кольцо падает в неоднородном магнитном поле под действием силы тяжести, то в нем течет индукционный ток. Соответственно на кольцо действует сила Ампера. Ничего не вычисляя, можно быть уверенным в том, что эта сила Ампера будет направлена вверх, чтобы — согласно правилу Ленца — мешать силе тяжести, которая является причиной падения кольца, что влечет за собой изменение магнитного потока, а это приводит к появлению индукционного тока, на который действует сила Ампера, тормозящая падение…
Ниже рассматриваются опыты, в которых изучаются свойства токов Фуко.
На рис. 8.24 показан опыт, демонстрирующий падение тел в неоднородном магнитном поле. Неоднородное магнитное поле тормозит движение проводящих предметов из-за токов Фуко, возникающих в проводниках при изменении магнитного потока через них. Демонстрируется беспрепятственное падение диэлектрического деревянного диска между полюсами сильного электромагнита и медленное падение медного и алюминиевого дисков в магнитном поле, напоминающее движение тел в среде с большой вязкостью.

Рис. 8.24. Падение тел в неоднородном магнитном поле
При падении сильного постоянного магнита внутри вертикальной проводящей трубки в ее стенках возникают токи Фуко, тормозящие это падение. В опыте (рис. 8.25) демонстрируется свободное падение немагнитного алюминиевого цилиндра в разных трубках, а также маленького магнита в стеклянной трубке. Затем показывают замедление падения этого магнита в алюминиевой трубке и его очень медленное падение в толстостенной медной трубке.

Рис. 8.25. Падение магнита в трубках
На рис. 8.26 показано демпфирование колебаний маятника. Толстая сплошная медная пластина, прикрепленная на конце физического маятника, движется при его колебаниях между полюсами сильного электромагнита. Слабо затухающие колебания маятника после включения магнитного поля начинают быстро затухать, превращаясь практически в апериодические колебания. Если на конце маятника закрепить медную пластинку, разрезанную в виде гребенки, то сильное затухание колебаний маятника исчезает, поскольку токи Фуко уже не могут замыкаться в объеме проводника.

Рис. 8.26. Демпфирование колебаний маятника
В опыте на рис. 8.27 показана левитация сплошного проводящего кольца. Токи Фуко могут возникать не только в проводниках при их перемещении в неоднородном магнитном поле, но и при быстром изменении этого поля. сплошное кольцо из алюминия, надетое на вертикальный сердечник электромагнита, питаемого переменным током частотой 50 Гц, висит в воздухе. в то время как такое же, но разрезанное кольцо свободно падает на обмотку.

Рис. 8.27. Левитация сплошного проводящего кольца
На рис. 8.28 показано взаимодействие проводника и электромагнита. Толстый медный диск укреплен в подшипниках на оси с ручкой. Вблизи него на такой же оси закреплен электромагнит. Если вращать за ручку включенный электромагнит, то диск начинает вращаться в ту же сторону. Если же, наоборот, вращать за ручку диск вблизи электромагнита, то последний также начинает вращаться. Силы взаимодействия диска и электромагнита, похожие по характеру на силы вязкого трения, обусловлены возникновением токов Фуко в диске.

Рис. 8.28. Взаимодействие проводника и электромагнита
При перемещении сверхпроводника в магнитном поле возникающие в нем незатухающие токи Фуко не позволяют проникать вешнему полю внутрь него. Получается как бы зеркальное отражение магнита, отталкивающее его от сверхпроводника. На рис. 8.29 демонстрируется левитация маленького магнита над большой шайбой из высокотемпературного сверхпроводника (ВТСП-керамики), охлажденной до температуры жидкого азота (77 К), то есть ниже критической температуры перехода ВТСП-керамики в сверхпроводящее состояние.

Рис. 8.29. Левитация маленького магнита над большой шайбой из высокотемпературного сверхпроводника (ВТСП-керамики)
Тепловое действие токов Фуко используется в индукционных печах при плавке металла или приготовлении пищи. Такая печь, в сущности, является большой катушкой, питаемой высокочастотным током большой силы. Катушка создает переменный магнитный поток через помещенный в печь образец, а возникающие токи Фуко разогревают последний.
На рис. 8.30 демонстрируется тепловое действие токов Фуко. Алюминиевое кольцо надевают на сердечник электромагнита, питаемого переменным током частотой 50 Гц, и некоторое время удерживают плоскогубцами в переменном магнитном поле. Затем кольцо опускают в воду, и она закипает, показывая, что кольцо разогрелось индукционными токами до высокой температуры.

Рис. 8.30. Тепловое действие токов Фуко
Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока

Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре

Введем коэффициент пропорциональности L
|
|
(8.16) |
Коэффициент пропорциональности L называется индуктивностью контура.
|
Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока. |
Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.
|
В системе СИ единицей измерения индуктивности является генри (Гн)
|
Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции.
|
Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции. |
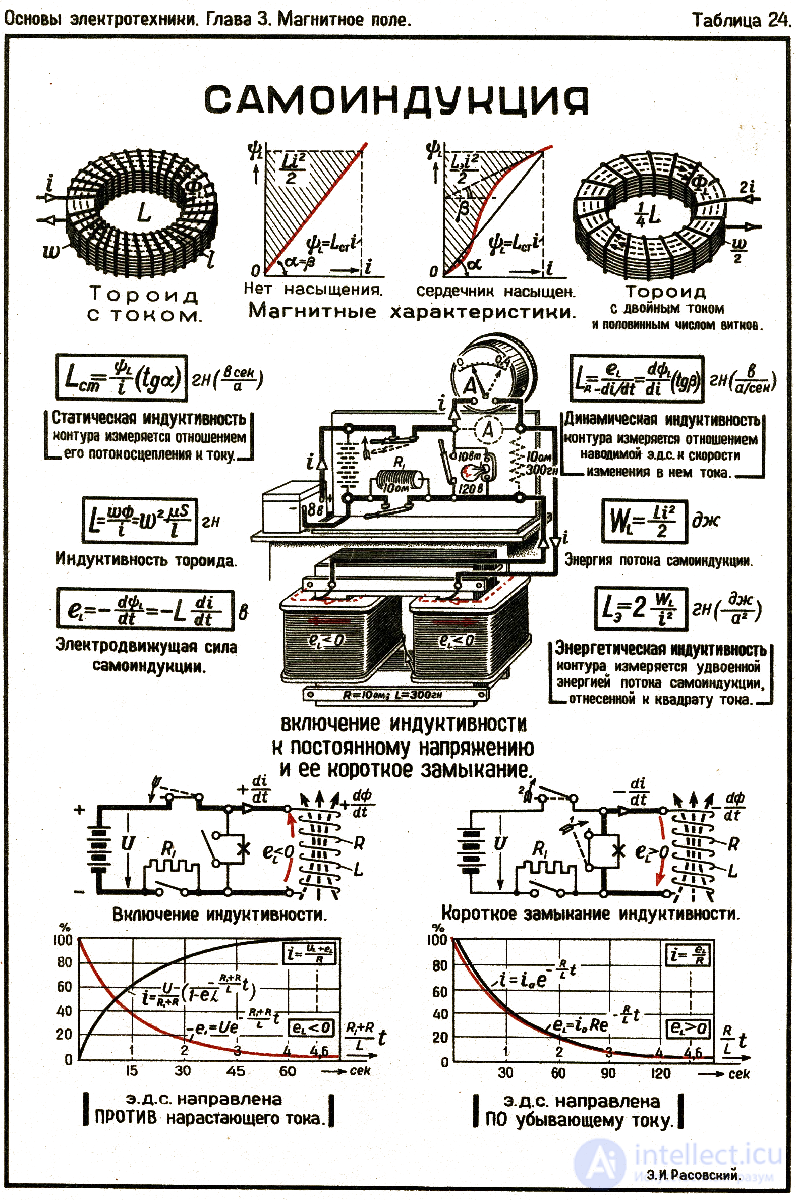
Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.
Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.
Выведем формулу для ЭДС самоиндукции  . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
. Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
|
|
(8.17) |
Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нем и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков
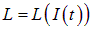 ,
,
что необходимо учитывать при дифференцировании

Подставляя это выражение в (8.17), получаем для неподвижного контура всреде
|
|
(8.18) |
Если же индуктивность контура не зависит от силы тока в нем, то имеем
|
|
(8.19) |
Мы приходим к закону самоиндукции. В этом простейшем случае:
|
В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи. |
Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна

где  — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно
— магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно  , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
, где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
|
|
(8.20) |
где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между  и I, получаем величину индуктивности длинного соленоида (рис. 8.31)
и I, получаем величину индуктивности длинного соленоида (рис. 8.31)
|
|
(8.21) |

Рис. 8.31. Индуктивность соленоида
При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Рассмотрим цепь, состоящую из сопротивления, индуктивности и источника тока (рис. 8.32).

Рис. 8.32. Цепь, содержащая катушку, сопротивлении и источник постоянного тока

Рис. 8.33. Токи замыкания (1) и размыкания (2) цепи с индуктивностью
Будем считать, что в сопротивление R уже включены соединенные с ним последовательно внутреннее сопротивление источника и сопротивление катушки. После того, как исчезнут экстра токи замыкания и размыкания и установится постоянный ток, сила тока в цепях, показанных на рис. 8.33, согласно закону Ома, будет равна

При разомкнутомключе ток не идет. Что будет, если ключ замкнуть, перебросив его из положения 1 в положение 2?
Обозначим через I мгновенное значение силы тока в цепи:  (функция времени). Если учесть ЭДС самоиндукции, то в каждый момент времени по-прежнему справедлив закон Ома
(функция времени). Если учесть ЭДС самоиндукции, то в каждый момент времени по-прежнему справедлив закон Ома
|
|
(8.22) |
Подставим в (8.22) выражение (8.19), предполагая, что индуктивность не зависит от тока. В результате применения закона Ома получаемдифференциальное уравнение для силы тока в цепи
|
|
(8.23) |
Это уравнение легко интегрируется

или

откуда следует общее решение уравнения (8.23)
|
|
(8.24) |
Постоянную интегрирования сonst определяем из начального условия: в момент времени t = 0 (замыкание ключа) тока в цепи еще не было, то есть I(0) = 0. Тогда

Таким образом, зависимость от времени тока замыкания в цепи с индуктивностью имеет вид
|
|
(8.25) |
Величина

имеет размерность времени и является характерным временем нарастания тока в цепи с индуктивностью. Сначала ток растет от нулевого значения линейно, затем скорость его роста начинает уменьшаться и ток асимптотически стремится к своему предельному значению

равному току в этой же цепи в отсутствие индуктивности. Практически предельное значение тока, учитывая реальную точность измерений силы тока, достигается за времена примерно равные  (рис. 8.34).
(рис. 8.34).

Рис. 8.34. Ток замыкания цепи с индуктивностью
Рассмотрим теперь рис. 8.33-2. Сначала ключ находился в положении 1, и в цепи шел ток

При перебрасывании ключа в положение2 источник тока отключается от цепи, и ток I начинает уменьшаться. Закон Ома для замкнутого участка цепи имеет теперь вид
|
|
(8.26) |
В отличие от (8.23) в разомкнутой цепи больше нет ЭДС  и действует только ЭДС самоиндукции. Уравнение (8.26) интегрируется еще легче
и действует только ЭДС самоиндукции. Уравнение (8.26) интегрируется еще легче
|
|
(8.27) |
Учитывая, что начальный ток в цепи был равен

для зависимости от времени тока размыкания в цепи с индуктивностью получаем
|
|
(8.28) |
На рис 8.35 представлен опыт, иллюстрирующий явления при замыкании и размыкании цепи, содержащей индуктивность. В цепь питания большой катушки индуктивности включена электрическая лампа. При замыкании цепи ключом лампа загорается не сразу, поскольку ЭДС самоиндукции препятствует изменению тока (правило Э.Х. Ленца). При размыкании наблюдается яркая вспышка из-за того, что источником тока становится ЭДС самоиндукции катушки, которая при резком изменении силы тока обычно заметно больше ЭДС источника.

Рис. 8.35. Явления при замыкании и размыкании цепи, содержащей индуктивность
Пример. К источнику с внутренним сопротивлением 2 Ом подключают катушку индуктивностью 0,5 Гн и сопротивлением 8 Ом. Найти время T, в течение которого после замыкания цепи ток в катушке достигнет значения, отличающегося от максимального на  .
.
Решение. В этой задаче полное сопротивление цепи равно

где r — внутреннее сопротивление источника, а  — сопротивление катушки. Согласно (8.25), ток в момент времени Т равен
— сопротивление катушки. Согласно (8.25), ток в момент времени Т равен
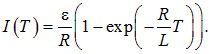
По условию задачи,

откуда

Обратимся снова к процессу замыкания цепи на рис. 8.33-1. Умножая правую и левую части уравнения (8.23) на  , получим
, получим
|
|
(8.29) |
Левая часть уравнения (8.29) выражает работу, совершаемую источником тока за время  . В правой части первое слагаемое есть величина работы, расходуемой на выделение джоулева тепла в проводнике. Ясно, что перед нами — уравнение закона сохранения энергии в рассматриваемой цепи. Каков же смысл второго слагаемого? Оно связано с катушкой, о чем свидетельствует множитель L, и представляет собой работу, затраченную на преодоление противодействия ЭДС самоиндукции. Куда же девается эта работа? В процессе замыкания цепи
. В правой части первое слагаемое есть величина работы, расходуемой на выделение джоулева тепла в проводнике. Ясно, что перед нами — уравнение закона сохранения энергии в рассматриваемой цепи. Каков же смысл второго слагаемого? Оно связано с катушкой, о чем свидетельствует множитель L, и представляет собой работу, затраченную на преодоление противодействия ЭДС самоиндукции. Куда же девается эта работа? В процессе замыкания цепи в катушкой создается магнитное поле. Значит, указанная работа аккумулируется именно в катушке как запасенная в ней энергия ее магнитного поля. Ток возрастает от нуля до некого установившегося значения I. Поэтому полная энергия поля катушки равна
|
|
(8.30) |
Поскольку
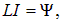
этот же результат можно записать в формах
|
|
(8.31) |
Эти формулы очень похожи на выражения для энергии конденсатора как функции его заряда или разности потенциалов на обкладках. Мы помним, что их можно привести к виду, где явно выделен объем конденсатора. Это позволило нам связать плотность энергии электрического поля с его напряженностью. Выполним аналогичную программу и для магнитного поля, используя в качестве «катушки» достаточно длинный соленоид.
Индуктивность соленоида дается выражением (8.21)
Магнитная индукция в соленоиде определяется по формуле (7.18)

Выразим плотность числа витков в соленоиде через магнитное поле в нем

и подставим в выражение для индуктивности соленоида. Получим
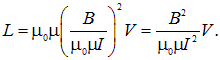
Наконец, подставим это выражение в формулу (17.28) для энергии поля в катушке
|
|
(8.32) |
Мы достигли своей цели: параметры соленоида, с которого мы начали, не присутствуют в этой формуле. Мы все выразили через магнитную индукцию поля, и энергия в катушке оказалась пропорциональной ее объему. Отсюда следует выражение для плотности энергии магнитного поля (неважно, чем и как созданного)
|
|
(8.33) |
Вспоминая связь напряженности магнитного поля с магнитной индукцией

находим эквивалентные представления для плотности энергии магнитного поля:
|
|
(8.34) |
Для магнитного поля в вакууме следует положить во всех этих формулах  . Нетрудно заметить сходство (8.34) с аналогичными формулами (3.35), (3.36) для электрического поля (рис. 8.36, рис. 8.37).
. Нетрудно заметить сходство (8.34) с аналогичными формулами (3.35), (3.36) для электрического поля (рис. 8.36, рис. 8.37).

Рис. 8.36. Мощное магнитное поле Солнца производит выбросы плазмы

Рис. 8.37. Мощное магнитное поле нейтронной звезды
Пример. Сравнить энергии, содержащиеся в объеме 1 л, если он пронизан: 1) однородным электрическим полем с напряженностью Е = 100 кВ/м; 2) однородным магнитным полем с индукцией В = 1 Тл.
Решение. Энергия электрического поля равна

Энергия магнитного поля равна

Оба указанных поля считаются достаточно сильными, но могут быть созданы без особых проблем. Задача демонстрирует, что практически выгоднее накапливать энергию в магнитном поле: в данном примере отношение энергий равно
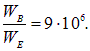
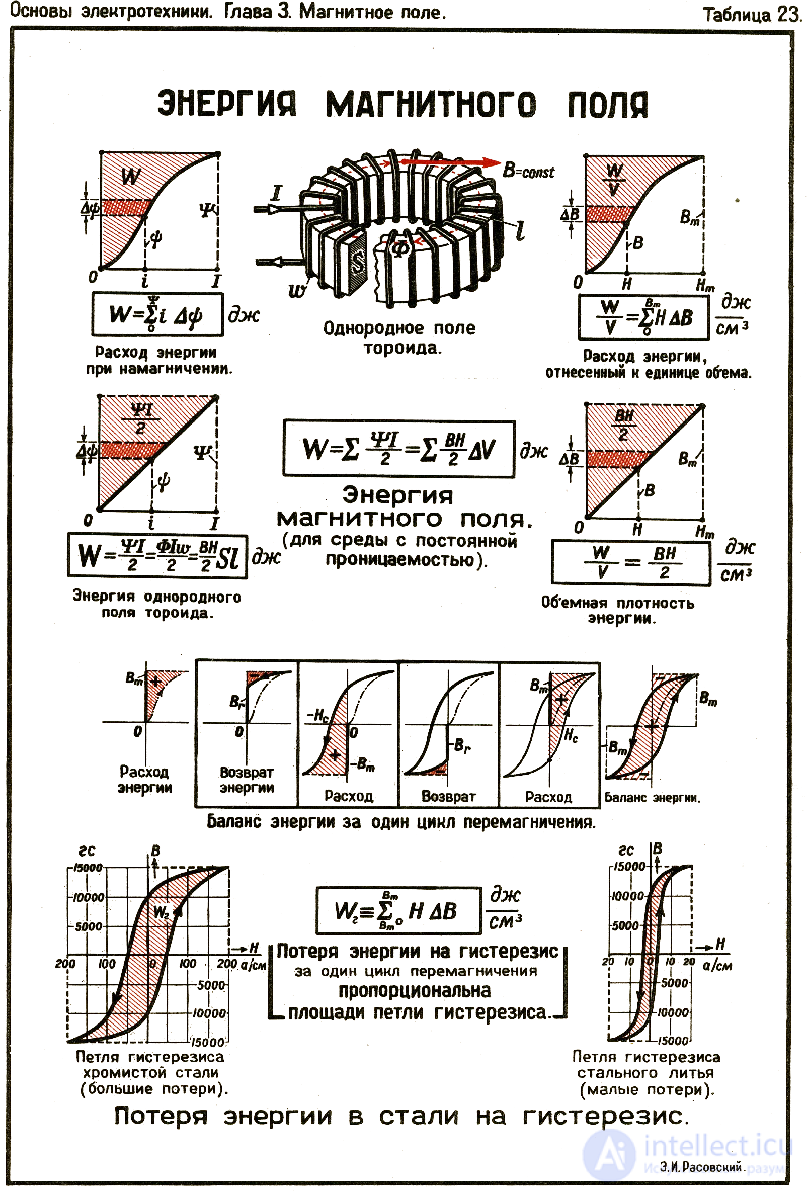
взаимоиндукция (взаимная индукция) — явление возникновения ЭДС индукции в одном контуре при изменении силы тока во втором контуре и наоборот. Взаимоиндукция — частный случай электромагнитной индукции .
При изменении силы тока в первом контуре, во втором возникает ЭДС:
где
— электродвижущая сила во втором контуре,
— потокосцепление первого контура,
— сила тока в первом контуре,
— взаимная индуктивность контуров.
При изменении силы тока во втором контуре, в первом возникает ЭДС:
где
— электродвижущая сила в первом контуре,
— потокосцепление второго контура,
— сила тока во втором контуре,
— взаимная индуктивность контуров.
Явление взаимоиндукции применяется для повышения и понижения напряжения переменного тока в трансформаторах.
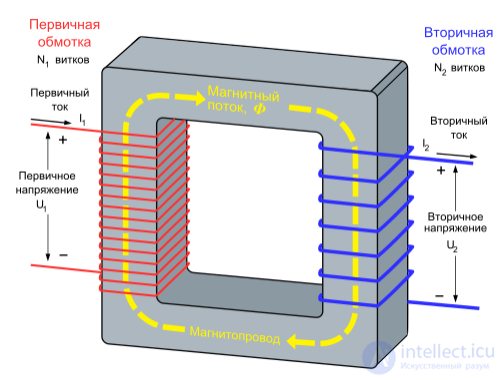
Возникновение ЭДС индукции во вторичной обмотке трансформатора
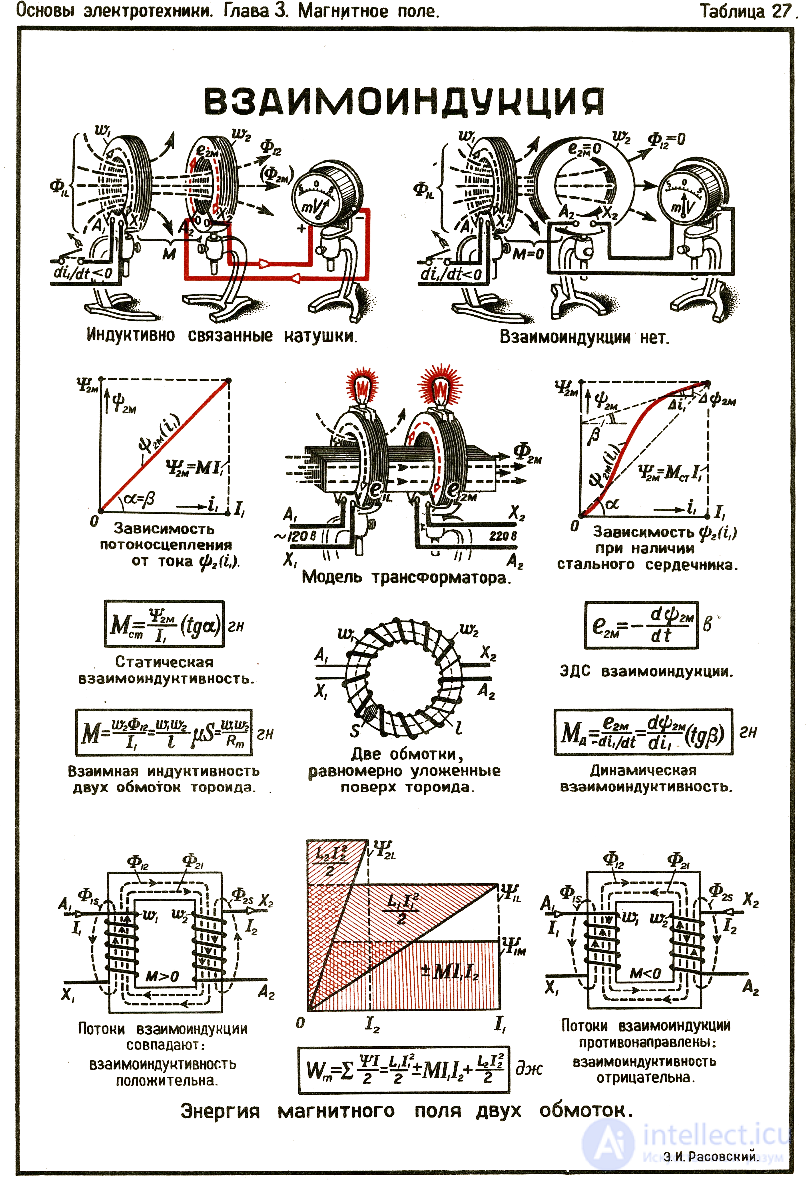
Рассмотрим систему проводов, по которым текут токи  . Магнитная проницаемость среды предполагается произвольной функцией координат, но ее зависимостью от магнитного поля Hпренебрегается.
. Магнитная проницаемость среды предполагается произвольной функцией координат, но ее зависимостью от магнитного поля Hпренебрегается.
Поток вектора магнитной индукции  через конкретный виток есть сумма потоков от каждого витка, пропорциональных току в этих витках
через конкретный виток есть сумма потоков от каждого витка, пропорциональных току в этих витках
|
|
(8.35) |
Коэффициент  , при условии
, при условии  , называются коэффициентами взаимной индукции. Важным свойством этих коэффициентов является их симметрия:
, называются коэффициентами взаимной индукции. Важным свойством этих коэффициентов является их симметрия: 
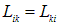
Онизависят только от взаимного расположения контуров. В Приложении доказана формула для энергии магнитного поля
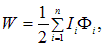
Подставляя сюда выражение (8.35), получим
|
|
(8.36) |
Отсюда сразу следует равенство коэффициентов взаимной индукции. Действительно,
|
|
(8.37) |
Доказательство именно этого равенства было целью данной статьи. При этом подразумевается использование таких понятий, как векторный потенциал и уравнения Максвелла. Интересно, что тот же результат может быть получен и другим, еще более простым путем.
Явление взаимной индуктивности приводит к образованию индукционного тока в одном контуре при изменение потока магнитного поля другого контура (рис. 8.38, 8.39).

Рис. 8.38. Взаимная индукция

Рис. 8.39 Тороидальный трансформатор
Рассмотрим два (бесконечно) малых покоящихся витка с токами I1 и I2 . По третьему закону Ньютона
|
|
(8.38) |
где, например, 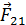 есть сила, действующая на второй виток со стороны первого.
есть сила, действующая на второй виток со стороны первого.
Если выбрать ось x вдоль линии, соединяющей контуры, то для силы, действующей на виток, имеем
|
|
(8.39) |
 — индукция магнитного поля в точке расположения витка с магнитным моментом
— индукция магнитного поля в точке расположения витка с магнитным моментом 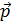 .
.
В нашем случае должно выполняться равенство
|
|
(8.40) |
как следствие уравнений (8.38) и (8.39). Здесь B1(2) — индукция магнитного поля в области витка 1(2), с бесконечно малым вектором площади 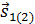 , магнитный момент которого
, магнитный момент которого 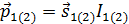 . Вместе с уравнением (8.40), это означает, что
. Вместе с уравнением (8.40), это означает, что
|
|
(8.41) |
с точностью до аддитивной константы, которая очевидно равна нулю. Поток вектора магнитной индукции через бесконечно малый контур есть по определению 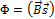 . Подставляя это выражение для витков 1 и 2 в (8.41), имеем
. Подставляя это выражение для витков 1 и 2 в (8.41), имеем
|
|
(8.42) |
Кроме того, по определению коэффициентов взаимной индукции, имеем
 .
.
Подстановка этих равенств в (8.42) приводит к требуемому равенству коэффициентов взаимной индукции для малых витков.
Дальнейшее доказательство равенства для витков с током произвольной формы не представляет труда. Действительно, любой большой виток можно разбить на много маленьких, после чего нетрудно получить тот же результат для произвольного контура. Таким образом, равенство коэффициентов взаимной индукции есть прямое следствие третьего закона Ньютона.
Известно, что в присутствии ферромагнетиков правило (8) может не выполняться. Тем не менее, и в этом случае возможно выполнение подобного равенства. Проиллюстрируем равенство (1) на конкретном примере тороидального сердечника, сделанного из ферромагнетика. Приведем распространенную ситуацию, когда на сердечник намотаны два контура с различным числом витков. Магнитное поле, создаваемое токами, протекающими по обоим контурам, практически полностью сосредоточено в ферромагнетике.
Если в контуре «1» течет ток  , то в контуре «2» потокосцепление есть
, то в контуре «2» потокосцепление есть

Аналогично, при протекании в контуре «2» тока  возникает магнитный поток (потокосцепление), пронизывающий контур «1»
возникает магнитный поток (потокосцепление), пронизывающий контур «1»

Здесь 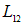 и
и  — коэффициенты взаимной индукции.
— коэффициенты взаимной индукции.
По первой обмотке течет ток  , который порождает магнитное поле H1, величина которого легко вычисляется по теореме о циркуляции
, который порождает магнитное поле H1, величина которого легко вычисляется по теореме о циркуляции

Здесь C — замкнутый путь длины l, проходящий внутри ферромагнетика. Поток магнитной индукции, проходящий через сечение сердечника, легко находится

Следовательно, потокосцепление через контур «2»:

Мы получили выражение для коэффициентов взаимной индукции, симметричное относительно индексов 1 и 2. Поэтому очевидно, что аналогичные рассуждения для второго контура приведут к тому же результату и, значит, к выполнению равенства коэффициентов взаимной индукции.
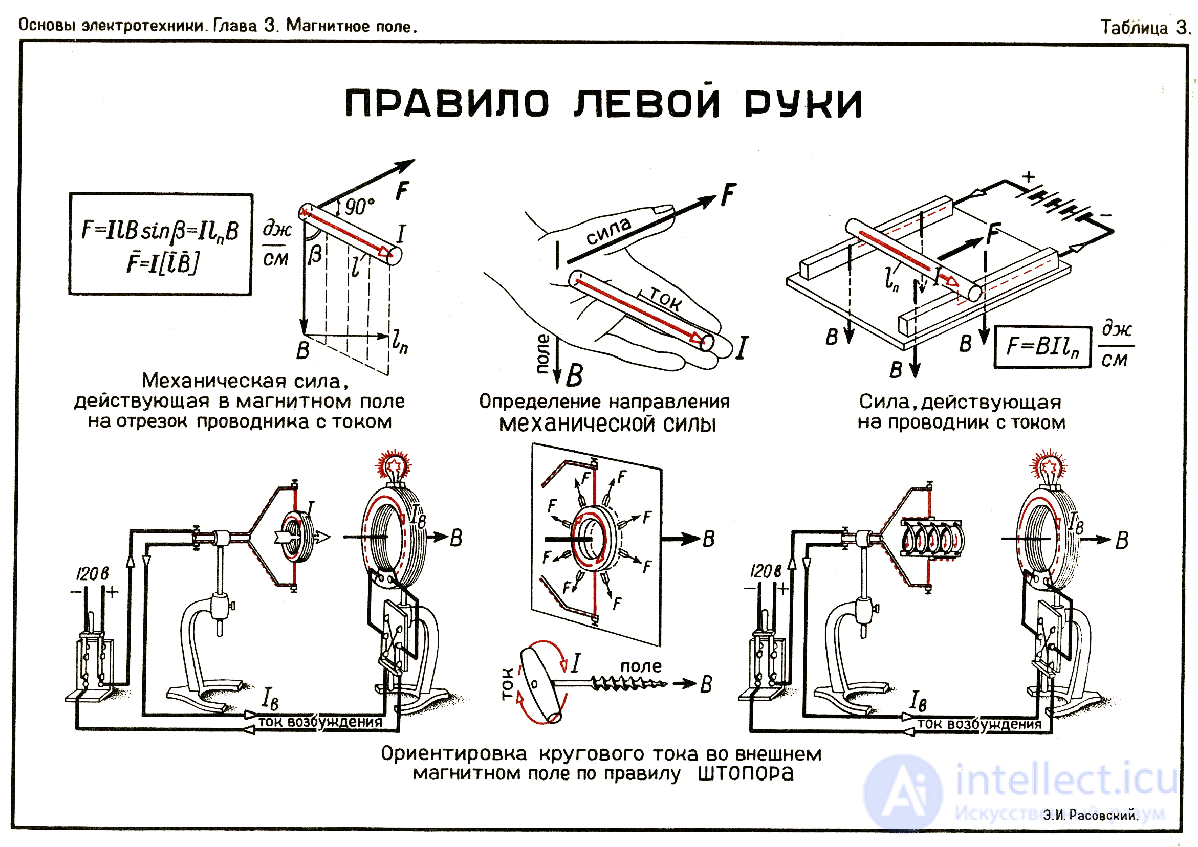
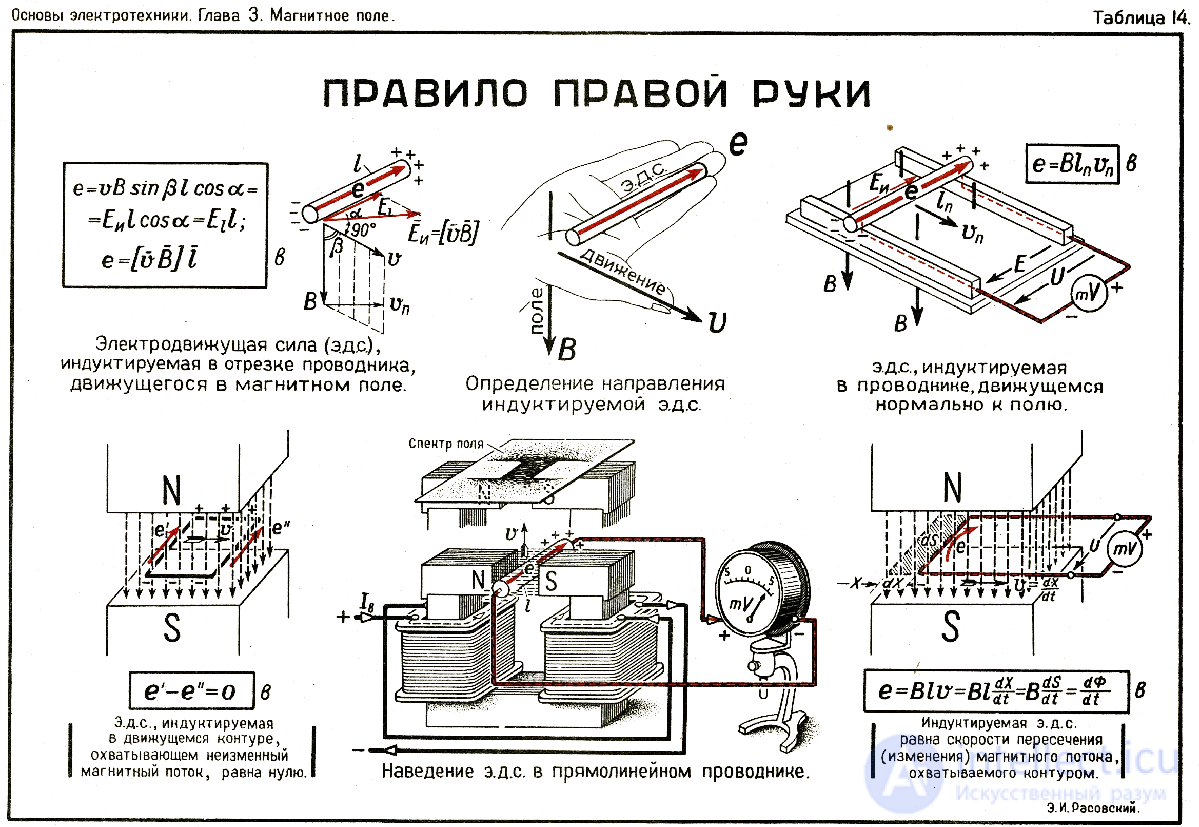

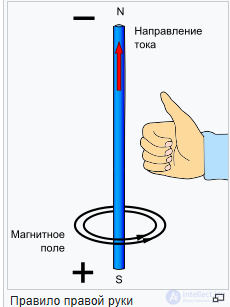
рис правило левой руки ,правило буравчика,правило штопора
Правило буравчика (правило винта) — любое из множества вариантов мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.
Как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным; он лишь должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, описанные в этой статье: они позволяют всегда придерживаться одного и того же выбора.
Правила левой руки
Первое правило левой руки
Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили во внутреннюю сторону ладони, перпендикулярно[g] к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей со стороны магнитного поля на проводник с током. Эта сила называется силой Ампера.Второе правило левой руки
Если движется заряд, а магнит покоится, то для определения направления силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили во внутреннюю сторону ладони перпендикулярно к ней, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера».
Энергия магнитного поля системы контуров с токами
Энергия магнитного поля системы контуров с токами требует знания теоремы Стокса, формулы Остроградского — Гаусса и уравнений Максвелла. При первом чтении можно пропустить
Используем известное выражение для энергии магнитного поля
|
|
(П1) |
Здесь 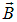 и
и  — индукция и напряженность магнитного поля, причем
— индукция и напряженность магнитного поля, причем  . Предполагается, что магнитная проницаемость не зависит от
. Предполагается, что магнитная проницаемость не зависит от  , т. е. среда не ферромагнитна. Интегрирование ведется по всему объему, занимаемому магнитным полем. Нас будет интересовать энергия всей системы (контуров с током), поэтому объем предполагается достаточно большим, чтобы на его поверхности магнитное поле отсутствовало. Выразим скалярное произведение через векторный потенциал
, т. е. среда не ферромагнитна. Интегрирование ведется по всему объему, занимаемому магнитным полем. Нас будет интересовать энергия всей системы (контуров с током), поэтому объем предполагается достаточно большим, чтобы на его поверхности магнитное поле отсутствовало. Выразим скалярное произведение через векторный потенциал 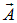 . Используя связь магнитного поля и векторного потенциала,
. Используя связь магнитного поля и векторного потенциала,  , а также основные формулы векторного анализа, получим:
, а также основные формулы векторного анализа, получим:

При интегрировании по всему объему второе слагаемое исчезает. Действительно:
|
|
(П2) |
Последнее равенство справедливо, поскольку интегрирование ведется по поверхности, охватывающей всю область, занятую магнитным полем. Как уже говорилось, H = 0 на этой поверхности. Далее воспользуемся уравнением Максвелла
|
|
(П3) |
которое справедливо в отсутствии электрических полей. Подставляя (П3), (П2) в (П1), получим

Это общее выражение, при его выводе не делались предположения о форме плотности тока проводимости j. Пусть теперь эта плотность тока создается контурами с токами Ii
Тогда  только в областях, занятых тонкими проводами. Выбрав линейный элемент провода
только в областях, занятых тонкими проводами. Выбрав линейный элемент провода  с поперечным сечением
с поперечным сечением  , можно записать
, можно записать

Здесь учтено, что все три вектора сонаправлены. Тогда, поскольку это равенство верно для всех контуров со своими
токами  , получаем выражение для энергии «n» контуров с током в виде
, получаем выражение для энергии «n» контуров с током в виде

Интегрирование ведется по всем объемам Vi , в которых плотность тока отлична от нуля.
Используя теорему Стокса для векторного потенциала 
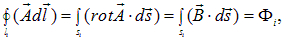

получаем окончательное выражение для энергии магнитного поля
|
|
(П4) |
Здесь Fi — поток вектора магнитной индукции через поверхность, охватываемую i-тым контуром тока. Он создается магнитными полями всех контуров с токами.
В основном тексте связь коэффициентов взаимной индуктивности получена на основе формулы (П4).
Исследование, описанное в статье про электромагнитная индукция, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электромагнитная индукция, правило левой руки, правило буравчика, правило штопора, правило правой руки, самоиндукция, взаимоиндукция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Базовая физика
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика