Лекция
Привет, Вы узнаете о том , что такое цепи с распределенными параметрами, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое цепи с распределенными параметрами, длинные линии , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
цепи с распределенными параметрами - это такие электрические цепи, в которых напряжения и токи на различных участках даже неразветвленной цепи отличаются друг от друга, т.е. являются функциями двух независимых переменных: времени t и пространственной координаты x.
Электромагнитные волны распространяются с конечной скоростью. Это
придает процессам, происходящим в электрических цепях, волновой характер, т.е.
токи и напряжения в электрической цепи оказываются зависящими не только от
времени t, но и от координаты сечения цепи x, т.е. U(x,t); i(x,t).
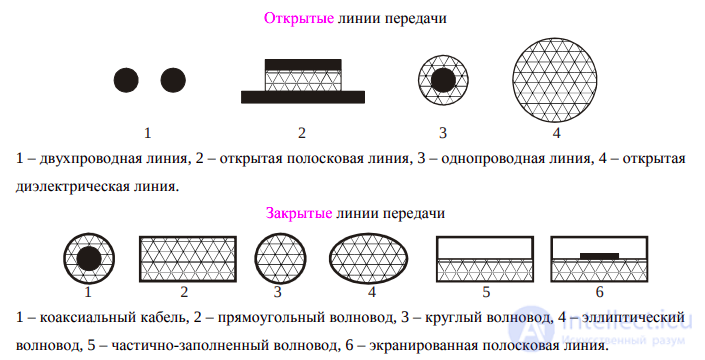
• Eсли λ>L, то цепь с сосредоточенными параметрами.
• Если λ одновременно свойствами R, L, C-элементов, т.е. параметры элементов как бы распределены по всему участку цепи.
Примерамы цепей с распределенными параметрами :
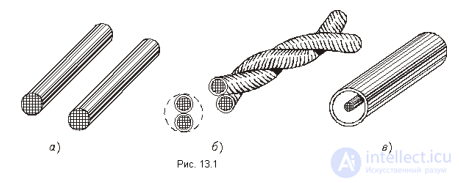
В предыдущих лекциях рассматривались электрические цепи, геометрические размеры которых, а также входящих в них элементов не играли роли, т.е. электрические и магнитные поля были локализованы соответственно в пределах конденсатора и катушки индуктивности, а потери мощности – в резисторе. Однако на практике часто приходится иметь дело с цепями (линии электропередачи, передачи информации, обмотки электрических машин и аппаратов и т.д.), где электромагнитное поле и потери равномерно или неравномерно распределены вдоль всей цепи. В результате напряжения и токи на различных участках даже неразветвленной цепи отличаются друг от друга, т.е. являются функциями двух независимых переменных: времени t и пространственной координаты x. Такие цепи называются цепями с распределенными параметрами. Смысл данного названия заключается в том, что у цепей данного класса каждый бесконечно малый элемент их длины характеризуется сопротивлением, индуктивностью, а между проводами – соответственно емкостью и проводимостью.
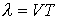 . Если
. Если 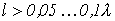 , то линию следует рассматривать как цепь с распределенными параметрами. Например, для
, то линию следует рассматривать как цепь с распределенными параметрами. Например, для 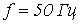 , т.е. при
, т.е. при 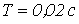 , и
, и 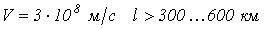 . Для
. Для 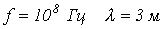 , т.е. уже при
, т.е. уже при 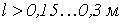 к линии следует подходить как к цепи с распределенными параметрами.
к линии следует подходить как к цепи с распределенными параметрами.
Для исследования процессов в цепи с распределенными параметрами (другое название – длинная линия) введем дополнительное условие о равномерности распределения вдоль линии ее параметров: индуктивности, сопротивления, емкости и проводимости. Такую линию называют однородной. Линию с неравномерным распределением параметров часто можно разбить на однородные участки.
длинные линии характеризуются первичными параметрами, то есть параметрами, отнесенными к единице длины линии. К первичным параметрам относят: 1. Резистивное сопротивление единицы длины линии  .
.
2. Индуктивность единицы длины линии  .
.
3. Емкость единицы длины линии 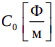 .
.
4. Проводимость единицы длины линии 
Под первичными параметрами линии будем понимать сопротивление 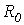 , индуктивность
, индуктивность  , проводимость
, проводимость  и емкость
и емкость 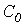 , отнесенные к единице ее длины. Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины
, отнесенные к единице ее длины. Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины 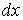 со структурой, показанной на рис. 1.
со структурой, показанной на рис. 1.
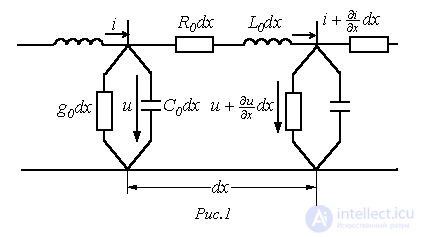
Пусть напряжение и ток в начале такого элементарного четырехполюсника равны u и i, а в конце соответственно 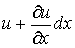 и
и  .
.
Разность напряжений в начале и конце участка определяется падением напряжения на резистивном и индуктивном элементах, а изменение тока на участке равно сумме токов утечки и смещения через проводимость и емкость. Таким образом, по законам Кирхгофа

или после сокращения на 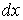
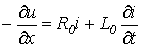 ; ; |
(1) |
 . . |
(2) |
Теорию цепей с распределенными параметрами в установившихся режимах будем рассматривать для случая синусоидального тока. Тогда полученные соотношения при 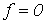 можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока.
можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока.
Вводя комплексные величины и заменяя 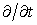 на
на 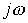 , на основании (1) и (2) получаем
, на основании (1) и (2) получаем
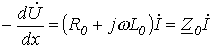 ; ; |
(3) |
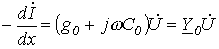 , , |
(4) |
где 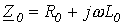 и
и 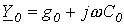 - соответственно комплексные сопротивление и проводимость на единицу длины линии.
- соответственно комплексные сопротивление и проводимость на единицу длины линии.
Продифференцировав (3) по х и подставив выражение 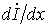 из (4), запишем
из (4), запишем
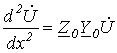 .
.
Характеристическое уравнение
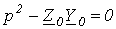 ,
,
откуда
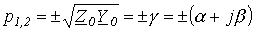 .
.
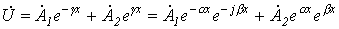 , , |
(5) |
где 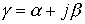 - постоянная распространения;
- постоянная распространения; 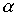 - коэффициент затухания;
- коэффициент затухания;  - коэффициент фазы.
- коэффициент фазы.
Для тока согласно уравнению (3) можно записать
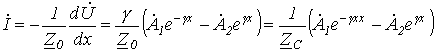 , , |
(6) |
где 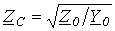 - волновое сопротивление.
- волновое сопротивление.
Волновое сопротивление  и постоянную распространения
и постоянную распространения 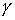 называют вторичными параметрами линии, которые характеризуют ее свойства как устройства для передачи энергии или информации.
называют вторичными параметрами линии, которые характеризуют ее свойства как устройства для передачи энергии или информации.
Определяя 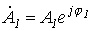 и
и 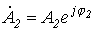 , на основании (5) запишем
, на основании (5) запишем
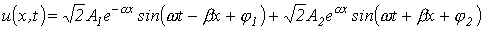 . . |
(7) |
Аналогичное уравнение согласно (6) можно записать для тока.
Слагаемые в правой части соотношения (7) можно трактовать как бегущие волны: первая движется и затухает в направлении возрастания х, вторая – убывания. Об этом говорит сайт https://intellect.icu . Действительно, в фиксированный момент времени каждое из слагаемых представляет собой затухающую (вследствие потерь энергии) гармоническую функцию координаты х, а в фиксированной точке – синусоидальную функцию времени.
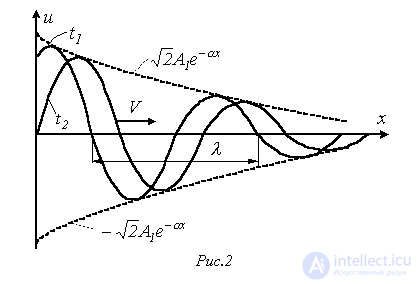
Волну, движущую от начала линии в сторону возрастания х, называют прямой, а движущуюся от конца линии в направлении убывания х – обратной.
На рис. 2 представлена затухающая синусоида прямой волны для моментов времени 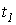 и
и 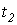
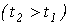 . Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения по линии неизменного фазового состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны:
. Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения по линии неизменного фазового состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны:
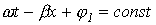 . . |
(8) |
Продифференцировав (8) по времени, получим
 . . |
(9) |
Длиной волны  называется расстояние между двумя ее ближайшими точками, различающимися по фазе на
называется расстояние между двумя ее ближайшими точками, различающимися по фазе на 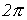 рад. В соответствии с данным определением
рад. В соответствии с данным определением
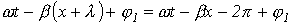 ,
,
откуда
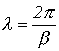
и с учетом (9)
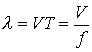 .
.
В соответствии с введенными понятиями прямой и обратной волн распределение напряжения вдоль линии в любой момент времени можно трактовать как результат наложения двух волн: прямой и обратной, - перемещающихся вдоль линии с одинаковой фазовой скоростью, но в противоположных направлениях:
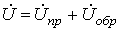 , , |
(10) |
где в соответствии с (5) 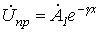 и .
и .
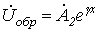 а к нижнему.
а к нижнему.
Аналогично для тока на основании (6) можно записать
 , , |
(11) |
где 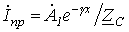 и
и  .
.
Положительные направления прямой и обратной волн тока в соответствии с (11) различны: положительное направление прямой волны совпадает с положительным направлением тока 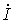 (от начала к концу линии), а положительное направление обратной волны ему противоположно.
(от начала к концу линии), а положительное направление обратной волны ему противоположно.
На основании (10) и (11) для прямых и обратных волн напряжения и тока выполняется закон Ома
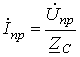 |
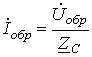 |
Рассмотрим теоретически важный случай бесконечно длинной однородной линии.
В случае бесконечно длинной линии в выражениях (5) и (6) для напряжения и тока слагаемые, содержащие 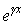 , должны отсутствовать, т.к. стремление
, должны отсутствовать, т.к. стремление 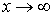 лишает эти составляющие физического смысла. Следовательно, в рассматриваемом случае
лишает эти составляющие физического смысла. Следовательно, в рассматриваемом случае 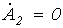 . Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным
. Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным
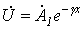 |
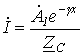 |
(12) |
На основании соотношений (12) можно сделать важный вывод, что для бесконечно длинной линии в любой ее точке, в том числе и на входе, отношение комплексов напряжения и тока есть постоянная величина, равная волновому сопротивлению:
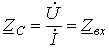 .
.
Таким образом, если такую линию мысленно рассечь в любом месте и вместо откинутой бесконечно длинной части подключить сопротивление, численно равное волновому, то режим работы оставшегося участка конечной длины не изменится. Отсюда можно сделать два вывода:
Уравнения бесконечно длинной линии распространяются на линию конечной длины, нагруженную на сопротивление, равное волновому. В этом случае также имеют место только прямые волны напряжения и тока.
У линии, нагруженной на волновое сопротивление, входное сопротивление также равно волновому.
Режим работы длинной линии, нагруженной на сопротивление, равное волновому, называется согласованным, а сама линия называется линией с согласованной нагрузкой.
Отметим, что данный режим практически важен для передачи информации, поскольку характеризуется отсутствием отраженных (обратных) волн, обусловливающих помехи.
Согласованная нагрузка полностью поглощает мощность волны, достигшей конца линии. Эта мощность называется натуральной. Поскольку в любом сечении согласованной линии сопротивление равно волновому, угол сдвига  между напряжением и током неизменен. Таким образом, если мощность, получаемая линией от генератора, равна
между напряжением и током неизменен. Таким образом, если мощность, получаемая линией от генератора, равна 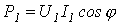 , то мощность в конце линий длиной
, то мощность в конце линий длиной 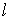 в данном случае
в данном случае
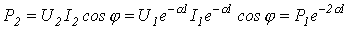 ,
,
откуда КПД линии
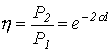
и затухание
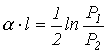 .
.
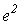 раз, а по напряжению или току – в
раз, а по напряжению или току – в  раз.
раз.
Наиболее типичными применениями длинных линий являются:
1) Средства связи (средства передачи сигналов от источника сигнала к нагрузке).
2) Линия задержки.
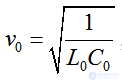 , где L0, C0 – погонные параметры, сигнал на нагрузке будет выделяться с задержкой, при этом tзад = L/v0. Поскольку линия нагружена на волновое сопротивление Zв, то искажения сигнала не происходит. Если Zв = Zн, то сигнал наблюдается с искажениями формы.
, где L0, C0 – погонные параметры, сигнал на нагрузке будет выделяться с задержкой, при этом tзад = L/v0. Поскольку линия нагружена на волновое сопротивление Zв, то искажения сигнала не происходит. Если Zв = Zн, то сигнал наблюдается с искажениями формы.
3) Трансформатор сопротивлений:
а) Четвертьволновой трансформатор сопротивлений.
Рассмотрим отрезок длинной линии, длина которой составляет четверть длины волны: L = λ/4, нагруженный на резистивное сопротивление Rн. Входное сопротивление такого отрезка определяется соотношением
Zвх = ρ2/ Rн.
Отсюда следует, что, изменяя отношение ρ/Rн, можно в широких пределах изменять входное сопротивление линии. Если необходимо преобразовать сопротивление Rн в R1н, то для этого сопротивление Rн надо включить через четвертьволновой отрезок с волновым сопротивлением ρ = (Rн R1н)1/2.
б) Металлический изолятор.
Выражение для входного сопротивления – четвертьволновой отрезок линии – показывает, что при Rн = 0 его входное сопротивление бесконечно. Это позволяет использовать его в качестве изолятора.
в) Колебательный контур.
В радиотехнике на СВЧ вместо колебательных контуров, составленных из L, C-элементов, используют двухполюсники в виде короткозамкнутых отрезков. Входное сопротивление короткозамкнутого отрезка линии определяется как
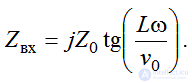 .
.
Если l = λ/2, то Zвх = ∞, т.е. четверть волнового отрезка длинной линии с коротким замыканием на конце обладает свойствами, аналогичными параллельному колебательному контуру.
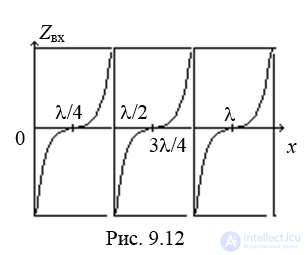
Определим частоты, на которых отрезок линии представляет собой параллельный колебательный контур, т.е. имеет максимум модуля сопротивления

Отсюда 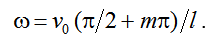 . На этих частотах данный отрезок будет представлять собой параллельный колебательный контур (рис. 9.12).
. На этих частотах данный отрезок будет представлять собой параллельный колебательный контур (рис. 9.12).
4) Формирователь коротких прямоугольных импульсов.
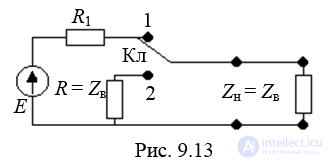
Если к согласованной длинной линии подключить источник постоянного напряжения E (рис. 9.13), то в ней по всей длине устанавливается одинаковое напряжение – линия заряжается (ключ в положении 1).
Если ключ переключить в положение 2, то на сопротивлении R = Zв формируется импульс напряжения прямоугольной формы, длительность которого равна удвоенному времени задержки линии.
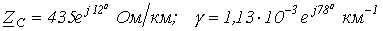 .
. ,
, 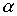 и
и 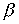 для кабеля, у которого
для кабеля, у которого 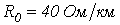 ,
, 
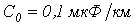 , если частота
, если частота 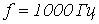 .
.
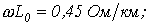
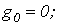
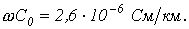
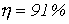 .
.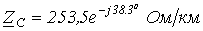 ;
; 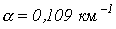 ;
; 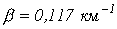 .
.
Исследование, описанное в статье про цепи с распределенными параметрами, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое цепи с распределенными параметрами, длинные линии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники