Место в общей алгебре, топологии и теории множеств - Комплексные

Это продолжение увлекательной статьи про комплексные числа.

...

определение и применение, операции над ними, физический смысл" >, называются компонентами комплексной функции } Аналогично определяется функция нескольких комплексных переменных[28].

Наглядное представление комплексной функции графиком затруднительно, так как даже для функции одной комплексной переменной график требует четырех измерений (два на область определения и еще два для области значений). Если вместо значения функции рассматривать ее модуль то полученный рельеф функции размещается в трех измерениях и дает некоторое представление о поведении функции[29].

Все стандартные функции анализа — многочлен, дробно-линейная функция, степенная функция, экспонента, тригонометрические функции, обратные тригонометрические функции, логарифм — могут быть распространены на комплексную плоскость. При этом для них будут иметь место те же алгебраические, дифференциальные и другие тождества, что и для вещественного оригинала[28], например:

Для комплексных функций определяются понятия предела, непрерывности и производной так же, как в вещественном анализе, с заменой абсолютной величины на комплексный модуль[28].

Дифференцируемые комплексные функции (то есть функции, имеющие производную) обладают рядом особенностей по сравнению с вещественными[30].

• Вещественная и мнимая часть дифференцируемой функции — гармонические функции, связанные условиями Коши — Римана.
• Всякая дифференцируемая в некоторой окрестности точки комплексная функция дифференцируема неограниченное число раз в этой точке (то есть аналитична, или голоморфна).

Определенный интеграл для функций одной комплексной переменной, вообще говоря, зависит от пути интегрирования (то есть выбора кривой от начальной до конечной точки в комплексной плоскости). Однако если интегрируемая функция аналитична в односвязной области, то ее интеграл внутри этой области не зависит от пути[31].

Преобразования комплексной плоскости

Всякая комплексная функция может рассматриваться как преобразование комплексной плоскости (или как преобразование одной комплексной плоскости в другую). Примеры:

• — параллельный перенос, определяемый радиус-вектором точки
• , где — комплексное число с единичным модулем — поворот вокруг начала координат на угол, равный аргументу
• — зеркальное отражение относительно вещественной оси.

Поскольку любое движение на плоскости есть комбинация перечисленных трех преобразований, функции и дают общее выражение для движения на комплексной плоскости[32].

Другие линейные преобразования[32]:

• , где — положительное вещественное число, задает растяжение, масштаб которого зависит от (сжатие, если).
• Преобразования и , где — произвольные комплексные числа, задают преобразование подобия.
• Преобразование где — общий вид аффинного преобразования комплексной плоскости.

Важную роль в комплексном анализе играют дробно-линейные преобразования[33]:

При этом (иначе функция вырождается в константу). Характеристическое свойство дробно-линейного преобразования: оно переводит окружности и прямые в окружности и прямые. При этом образом окружности может оказаться прямая, и наоборот[33].

Среди других практически полезных функций преобразования: инверсия функция Жуковского.

Аналитическая геометрия на комплексной плоскости

Исследование плоских фигур нередко облегчается, если перенести их на комплексную плоскость. Многие теоремы планиметрии допускают наглядную и компактную запись с помощью комплексных чисел, например[34]:

• Три (различные) точки лежат на одной прямой тогда и только тогда, когда выполняется условие:

является вещественным числом.

• Четыре (различные) точки лежат на одной окружности (или на одной прямой) тогда и только тогда, когда выполняется условие:

отношение является вещественным числом.

• Если даны три вершины параллелограмма: то четвертая определяется равенством[35]:

Параметрическое уравнение прямой на комплексной плоскости имеет вид[36]:

где — комплексные числа, — произвольный вещественный параметр.

Угол между двумя прямыми и равен В частности, прямые перпендикулярны, когда — чисто мнимое число. Две прямые параллельны тогда и только тогда, когда есть вещественное число; если при этом также вещественно, то обе прямые совпадают. Каждая прямая рассекает комплексную плоскость на две полуплоскости: на одной из них выражение положительно, на другой — отрицательно[36].

Уравнение окружности с центром и радиусом имеет чрезвычайно простой вид: Неравенство описывает внутренность окружности[36]. Часто удобна параметрическая форма уравнения окружности[37]:

Место в общей алгебре, топологии и теории множеств

Множество комплексных чисел образует поле, которое является конечным расширением степени 2 поля вещественных чисел Основное алгебраическое свойство — оно алгебраически замкнуто, то есть в нем любой многочлен имеет (комплексные) корни и, следовательно, распадается на линейные множители. Говорят также, что есть алгебраическое замыкание[38] поля

Характеристика комплексного поля равна нулю, мощность как множества та же, что и у поля вещественных чисел, то есть континуум. Теорема Фробениуса установила, что существуют только два тела, являющиеся конечными расширениями — поле комплексных чисел и тело кватернионов[39].

Превратить поле комплексных чисел в упорядоченное поле невозможно, потому что в упорядоченном поле квадрат любого элемента неотрицателен, и мнимая единица в нем не может существовать.

Из свойств модуля следует, что комплексные числа образуют структуру двумерного нормированного пространства над полем

Поле допускает бесконечно много автоморфизмов, но только один из них (не считая тождественного) оставляет вещественные числа на месте[40].

Поля и — единственные связные локально компактные топологические поля[41].

Физический смысл комплексного числа

Долгое время комплексные числа считались абстрактной категорией, не применяется в реальном мире, однако за последние столетия было найдено много случаев, когда физические величины, представленные действительными числами, если их выразить через комплексные становятся значительно удобнее для расчетов. Вот несколько наиболее значимых примеров:

Электротехника

В электротехнике комплексные числа активно используются для расчета электрических цепей переменного тока. В таких кругах напряжение и сила тока рассматриваются как векторы, вращающиеся в некотором фазовом пространстве, смещены друг относительно друга на 90 °. Такие векторы естественно выражаются через комплексное число в форме Эйлера. Использование комплексных чисел позволяет удобным способом добавлять различные токи между собой.

Квантовая механика

В квантовой механике частицы всегда имеют волновую природу, вплоть до момента измерения, провоцирует коллапс волновой функции . Для того чтобы корректно представить это в математической форме, вводится комплексная функция, называется волновой , что позволяет выразить состояние любой квантовой системы.

Аэродинамика

Одна из самых важных в аэродинамике формул, преобразования Жуковского , используемый для построения оптимального профиля крыла, является функцией комплексной переменной.

Теория относительности

Пространство Минковского , что является математической интерпретацией четырехмерного пространства-времени нашей Вселенной, фактически имеет три действительных и одну воображаемую координату. Преобразования Лоренца можно выразить как поворот в этом пространстве.

Теория управления

В теории автоматического управления , уравнения в комплексных числах нужны для определения устойчивости системы - способность системы, автоматически управляется, возвращаться в установившийся режим после некоторого возмущения.

Некоторые практические применения

Те особенности комплексных чисел и функций, которые отличают их от вещественных, оказались полезными, а часто и незаменимыми в математике, в естественных науках и технике.

Математика

Приложения комплексных чисел сами по себе занимают видное место в математике — в частности, понятия алгебраических чисел, нахождение корней многочленов, теория Галуа, комплексный анализ и т. д.

Перенеся геометрическую задачу с обычной плоскости на комплексную, мы нередко получаем возможность значительно упростить ее решение[42][43].

Многие сложные задачи теории чисел (например, теория биквадратичных вычетов) и вещественного математического анализа (например, вычисление сложных или несобственных интегралов) удалось решить только с помощью средств комплексного анализа. Мощным инструментом для открытий в теории чисел оказались, например, гауссовы числа вида где — целые числа[44]. Для исследования распределения простых чисел понадобилась комплексная дзета-функция Римана[45].

Нередко проблемы вещественного анализа проясняются при их комплексном обобщении. Классический пример — разложение в ряд

Этот ряд сходится только в интервале , хотя точки не являются какими-то особенными для приведенной функции. Положение проясняется при переходе к функции комплексного переменного , у которой обнаруживаются две особые точки: . Соответственно, эту функцию можно разложить в ряд Тейлора только в круге единичного радиуса[46].

При решении линейных дифференциальных уравнений важно сначала найти все комплексные корни характеристического многочлена, а затем попытаться решить систему в терминах базовых экспонент[47]. В разностных уравнениях используются для аналогичной цели комплексные корни характеристического уравнения системы разностных уравнений[48]. С помощью теории вычетов, являющейся частью комплексного анализа, вычисляются многие сложные интегралы по замкнутым контурам[49]..

Исследование функции часто связано с анализом ее частотного спектра с помощью комплексного преобразования Фурье или Лапласа[50].

О представлении комплексных чисел в информатике и компьютерной поддержке комплексной арифметики см. статью Комплексный тип данных.

Конформное отображение

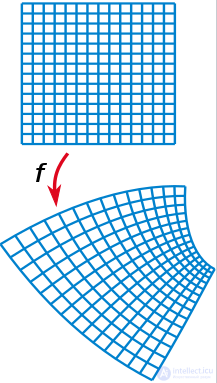
Пример конформного преобразования

Как уже отмечалось выше, всякая комплексная функция может рассматриваться как преобразование одной комплексной плоскости в другую. Гладкая (аналитическая) функция обладает двумя особенностями: если в заданной точке производная не равна нулю, то коэффициент растяжения/сжатия при этом преобразовании одинаков по всем направлениям, угол поворота также постоянен (конформное отображение)[51]. С этим фактом связано широкое применение комплексных функций в картографии[52][53] и гидродинамике[54].

Кроме широкого применения непосредственно в теории функции комплексного переменного, комплексные числа возникают в различных областях математики

Фракталы

Множество Мандельброта и множество Жулиа определяются как области, на которых некоторая итерационно определена последовательность комплексных чисел всегда будет иметь конечную верхнюю границу.

Теория чисел

Одна из проблем тысячелетия , гипотеза Римана , предполагает некоторую форму распределения нулей комплексной функции, называется дзета-функция Римана . Это распределение оказывается тесно связанным с распределением простых чисел .

Квантовая механика

Основой квантовой механики является понятие комплексной волновой функции, Для описания динамики квантовой системы используются дифференциальные уравнения с комплексными коэффициентами типа уравнения Шредингера. Решения этих уравнений заданы в комплексном гильбертовом пространстве. Операторы, соответствующие наблюдаемым величинам, эрмитовы. Коммутатор операторов координаты и импульса представляет собой мнимое число[55]:

Здесь — редуцированная постоянная Планка , то есть (постоянная Дирака).

Важную роль в квантовой механике играют матрицы Паули и матрицы Дирака, некоторые из них содержат комплексные значения[55].

Электротехника

Поскольку переменный ток есть колебательный процесс, его удобно описывать и исследовать с применением комплексных чисел. Вводятся также понятия импеданса или комплексного сопротивления для реактивных элементов электрической цепи таких как емкость и индуктивность — это помогает рассчитать токи в цепи[56]. Ввиду того, что традиционно символ в электротехнике обозначает величину тока, мнимую единицу там обозначают буквой [57]. Во многих областях электротехники (в основном радиочастотной и оптической) используется не запись уравнений тока и напряжения для цепи, а напрямую уравнения Максвелла в их спектральном представлении, физические величины которых заданы в комплексной плоскости, и при переходе из - в -пространство (где — время, — угловая частота) посредством преобразования Фурье получаются более простые уравнения без производных[58].

Сложные графики ( Раскраска доменов и риманова поверхность)

График цветового круга выражения ( г 2 - 1) ( г - 2 - я ) 2/г 2 + 2 + 2 я

При визуализации сложных функций необходимы как сложный ввод, так и вывод. Поскольку каждое комплексное число представлено в двух измерениях, визуальное отображение сложной функции потребует восприятия четырехмерного пространства , что возможно только в проекциях. Из-за этого были разработаны другие способы визуализации сложных функций.

При раскраске домена выходные размеры представлены цветом и яркостью соответственно. Каждая точка комплексной плоскости как домена украшена орнаментом , обычно цветом, представляющим аргумент комплексного числа, и яркостью, представляющей величину. Темные пятна обозначают модули, близкие к нулю, более яркие пятна находятся дальше от начала координат, градация может быть прерывистой, но предполагается монотонной. Цвета часто меняются в зависимости отπ/3от 0 до 2 π от красного, желтого, зеленого, голубого, синего до пурпурного. Эти графики называются графиками цветового круга . Это обеспечивает простой способ визуализации функций без потери информации. На рисунке показаны нули для ± 1, (2 + i) и полюса при ± √ −2−2i .

Римановы поверхности - еще один способ визуализировать сложные функции.Римановы поверхности можно рассматривать как деформации комплексной плоскости; в то время как горизонтальные оси представляют реальный и мнимый входы, единственная вертикальная ось представляет только реальный или мнимый выход. Однако римановы поверхности построены таким образом, что их поворот на 180 градусов показывает воображаемый результат, и наоборот. В отличие от раскраски областей, римановы поверхности могут представлять многозначные функции типа.

Логические основания

Расширение поля вещественных чисел до комплексных, как и любое другое расширение алгебраической структуры, ставит множество вопросов, основные из которых — как определить операции над новым типом чисел, какие свойства будут иметь новые операции и (главный вопрос) допустимо ли такое расширение, не приведет ли оно к неустранимым противоречиям. Для анализа подобных вопросов надо сформировать набор аксиом для комплексных чисел.

Аксиоматика комплексных чисел

Можно определить аксиоматику множества комплексных чисел , если опираться на аксиоматическую теорию вещественных чисел . Именно, определим как минимальное поле, содержащее множество вещественных чисел и квадратный корень из −1 (мнимую единицу). Более строго, аксиомы комплексных чисел следующие[59][60].

С1: Для всяких комплексных чисел определена их сумма .

С2: Сложение коммутативно:. Для краткости оговорку «для всяких» далее, как правило, опускаем.

С3: Сложение ассоциативно:

С4: Существует элемент 0 (ноль) такой, что .

С5: Для всякого комплексного числа существует «противоположный ему» элемент

С6: Для всяких комплексных чисел определено их произведение.

С7: Умножение коммутативно:

С8: Умножение ассоциативно:

С9: Умножение связано со сложением распределительным (дистрибутивным) законом:

С10: Существует элемент 1 (единица), не равный нулю и такой, что.

С11: Для всякого ненулевого числа существует «обратное ему» число такое, что

С12: Множество комплексных чисел содержит подполе, изоморфное полю вещественных чисел . Для простоты далее это подполе обозначается той же буквой.

С13: Существует элемент (мнимая единица) такой, что

С14 (аксиома минимальности): Пусть — подмножество , удовлетворяющее следующим условиям: оно содержит и мнимую единицу и замкнуто относительно сложения и умножения. Тогда совпадает со всем.

Из этих аксиом вытекают как следствия все прочие свойства. Первые 11 аксиом означают, что образует поле, а 12-я аксиома устанавливает, что это поле является расширением Приведенная аксиоматика категорична, то есть любые ее модели изоморфны[61].

Существуют и другие варианты

продолжение следует...

Продолжение:

Часть 1 Комплексные числа, определение и применение, операции над ними, физический смысл
Часть 2 Формы представления комплексного числа - Комплексные числа, определение и применение,
Часть 3 Место в общей алгебре, топологии и теории множеств - Комплексные
Часть 4 Вариации Обобщения и связанные с ними понятия - Комплексные числа,