Формы представления комплексного числа - Комплексные числа, определение и применение,

Это продолжение увлекательной статьи про комплексные числа.

...

угол в положительном направлении, а после умножения на радиус-вектор поворачивается на прямой угол в отрицательном направлении.

Модуль

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же самое, расстояние от точки комплексной плоскости до начала координат). Модуль комплексного числа обозначается (иногда или ) и определяется выражением[13]

.

Если является вещественным числом, то совпадает с абсолютной величиной этого числа в вещественном понимании термина.

Для любых имеют место следующие свойства модуля[13][15]:

1) { , причем тогда и только тогда, когда ;

2) (неравенство треугольника);

3) ;

4) .

5) Для пары комплексных чисел и модуль их разности равен расстоянию между соответствующими точками комплексной плоскости.

6) Модуль числа связан с вещественной и мнимой частями этого числа соотношениями:

Аргумент

Аргументом ненулевого комплексного числа называется угол между радиус-вектором соответствующей точки и положительной вещественной полуосью. Об этом говорит сайт https://intellect.icu . Аргумент числа измеряется в радианах и обозначается . Из этого определения следует, что[13]

.

Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до , где — любое целое число. Главным значением аргумента называется такое значение , что . Главное значение может обозначаться [16].

Некоторые свойства аргумента[15]:

1) Аргумент обратного числа отличается знаком от аргумента исходного:

2) Аргумент произведения равен сумме аргументов сомножителей:

3) Аргумент частного от деления равен разности аргументов делимого и делителя:

Сопряженные числа

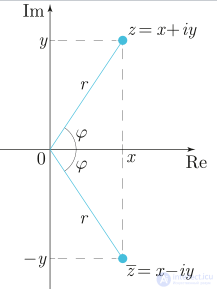
Геометрическое представление сопряженных чисел

Если комплексное число, то число называется сопряженным (или комплексно-сопряженным) к (обозначается также ). На комплексной плоскости сопряженные числа получаются друг из друга зеркальным отражением относительно вещественной оси. Модуль сопряженного числа такой же, как исходного, а их аргументы различаются знаком[17]:

• 

Переход к сопряженному числу можно рассматривать как одноместную операцию; она имеет следующие свойства[17]:

• тогда и только тогда, когда — вещественное число.
• (сопряженное к сопряженному есть исходное).

Произведение комплексно-сопряженных чисел — неотрицательное вещественное число, равное нулю только для нулевого z[15]:

• 

Сумма комплексно-сопряженных чисел — вещественное число[15]:

• 

Другие соотношения[15]:

• 
• 
• 
• 
• 

Обобщение: , где — произвольный многочлен с вещественными коэффициентами. В частности, если комплексное число является корнем многочлена с вещественными коэффициентами, то сопряженное число тоже является его корнем. Из этого следует, что комплексные корни такого многочлена, не являющиеся вещественными числами (имеющие ненулевую мнимую часть), разбиваются на пары комплексно-сопряженных[15].

Пример

Тот факт, что произведение есть вещественное число, можно использовать, чтобы выразить комплексную дробь в канонической форме, то есть избавиться от мнимости в знаменателе. Для этого надо умножить числитель и знаменатель на сопряженное к знаменателю выражение[18], например:

Формы представления комплексного числа

Алгебраическая форма

Выше использовалась запись комплексного числа в виде ; такая запись называется алгебраической формой комплексного числа. Две другие основные формы записи связаны с представлением комплексного числа в полярной системе координат.

Тригонометрическая форма

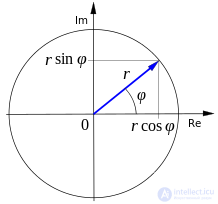
Тригонометрическое представление

Если вещественную и мнимую части комплексного числа выразить через модуль и аргумент (то есть , ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме[13]:

Как уже сказано выше, для нуля аргумент не определен; для ненулевого числа определяется с точностью до целого кратного .

Показательная форма

Фундаментальное значение в комплексном анализе имеет формула Эйлера[18]:

где — число Эйлера, , — функции косинуса и синуса, — комплексная экспонента, продолжающая вещественную на случай комплексного показателя степени.

Применяя эту формулу к тригонометрической форме, получим показательную форму комплексного числа[18]:

Следствия

(1) Модуль выражения где вещественно, равен 1.

(2) — при комплексном эти равенства могут служить определением косинуса и синуса.

Пример[19]. Представим в тригонометрической и показательной форме число

;

(поскольку находится в III координатной четверти).

Отсюда:

Формула Муавра и извлечение корней

Эта формула помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид[10]:

,

где — модуль, а — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формула справедлива при любом целом , не обязательно положительном.

Аналогичная формула применима также и при вычислении корней -й степени из ненулевого комплексного числа[18]:

Корни пятой степени из единицы (вершины пятиугольника)

Это значит, что корни-й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса с центром в начале координат (см. рисунок).

Для извлечения квадратного корня из комплексного числа, записанного в стандартном формате можно преобразовать это число в тригонометрическую форму и воспользоваться вышеприведенной формулой для Но существует и чисто алгебраическое представление для двух значений корня: где[20]:

Здесь — функция «знак», а радикалы обозначают обычный арифметический корень из неотрицательного вещественного числа. Формула легко проверяется возведением в квадрат.

Пример: для квадратного корня из формулы дают два значения:

История

Квадратные корни были известны еще в древнем Вавилоне , однако все древние авторы или вообще не рассматривали квадратные корни из отрицательных чисел, или же просто отмечали их невозможность.

Впервые, пожалуй, мнимые величины появились в известном труде «Великое искусство, или о правилах» алгебры Кардано ( 1545 ) во время развязку квадратного уравнения x 2 - 10x + 40 = 0, который однако, признал их "бессодержательными, хотя и хитроумными ". Польза мнимых величин, в частности, при решении кубического уравнения, в случае, когда действительные корни многочлена выражаются через кубический корень из мнимых величин, не приводится, впервые оценил Бомбелли ( 1572 ), хотя и он считал комплексные числа бесполезной игрушкой.

выражения вида , Появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI-XVII веках благодаря Декарту , что таким образом пытался подчеркнуть их нереально. В целом, для многих ученых того времени, природа комплексных чисел была непонятной, а их право на существование казалось довольно сомнительным, впрочем, это же можно сказать и об иррациональных и даже о отрицательные числа. Лейбниц , например, писал: «Дух Божий нашел тончайшую отдушину в этом чуде анализа, урод с мира идей, двойной сути, находящийся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Однако, тот факт, что применение методов работы с рациональными числами давало логические результаты и для комплексных, давало математикам повод для большего доверия.

Термин «мнимые» для этих величин был введен Рене Декартом в 1637 году, хотя он старался подчеркнуть их воображаемую природу.

[...] иногда только воображаемый, то есть можно представить столько, сколько я сказал в каждом уравнении, но иногда не существует количества, которое соответствует тому, что мы представляем. ([...] quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune Quantité qui correde à celle qu представьте себе.)

Долгое время было неясно, все операции над комплексными числами приводят к комплексным результатов, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корня степени n из данного числа была решена в работах Муавра (1707) и Котса ( 1722 ). Также Муавр заметил связь между комплексными числами и тригонометрическими функциями, благодаря чему он вывел известную формулу Муавра :

символ предложил Эйлер ( 1777 , опубл. 1794 ), взявший для этого первую букву слова лат. imaginarius . Он распространил все стандартные функции, включая логарифм , на комплексную область, а также вывел формулу Эйлера , связывающая комплексную экспоненту с тригонометрическими функциями. Эйлер также высказал в 1751 году мысль о замкнутости алгебры поля комплексных чисел. К такому же выводу пришел д'Аламбер (1747), но первый строгое доказательство этого факта принадлежит Гауссу ( 1799 ). Гаусс ввел во всеобщее употребление термин «комплексное число» в 1831году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году, а также понятие "нормы" a 2 + b 2 .

Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Каспара Весселя [en] (1799). Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 году. Современный геометрический смысл, иногда его еще называют «диаграммой Аргана», вошел в употребление после публикации в 1806-м и 1814-м годах работы Аргана, что повторяла независимо выводы Весселя. Именно Арганда ввел термин "модуль" для величины . Термины "аргумент" и "сопряженное число" ввел Коши. Благодаря этим работам, стал ясен тесная связь между комплексными числами и векторной алгеброй .

В 1806 году Арган с помощью комплексных чисел впервые опубликовал строгое доказательство основной теоремы алгебры - утверждения о том, что любой многочлен над полем комплексных чисел имеет комплексный корень. [10]

Арифметическая модель комплексных чисел как пары вещественных чисел была построена Гамильтоном ( 1837 ) это доказало непротиворечивость их свойств.

Успешность модели комплексных чисел как векторов на плоскости подтолкнула математиков к поискам подобной репрезентации трехмерного пространства. Однако эти поиски не привели к успеху, однако, 1843 году Гамильтон открыл тело кватернионов (векторов в четырехмерном пространстве), правда, отказавшись от качества коммутативности умножения для них.

Впервые, по-видимому, мнимые величины были упомянуты в труде Кардано «Великое искусство, или об алгебраических правилах» (1545), в рамках формального решения задачи по вычислению двух чисел, сумма которых равна 10, а произведение равно 40. Он получил для этой задачи квадратное уравнение, корни которого: и . В комментарии к решению он написал: «эти сложнейшие величины бесполезны, хотя и весьма хитроумны», и «арифметические соображения становятся все более неуловимыми, достигая предела столь же утонченного, сколь и бесполезного»[21].

Возможность использования мнимых величин при решении кубического уравнения впервые описал Бомбелли (1572), он же дал правила сложения, вычитания, умножения и деления комплексных чисел. Уравнение имеет вещественный корень , однако по формулам Кардано получаем: . Бомбелли обнаружил, что , так что сумма этих величин дает нужный вещественный корень. Он отметил, что в подобных (неприводимых) случаях комплексные корни уравнения всегда сопряжены, поэтому в сумме и получается вещественное значение. Разъяснения Бомбелли положили начало успешному применению в математике комплексных чисел[22][21].

Выражения, представимые в виде , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках с подачи Декарта, который называл их так, отвергая их реальность. Для многих других крупных ученых XVII века природа и право на существование мнимых величин представлялись весьма сомнительными. Лейбниц, например, в 1702 году писал: «Дух божий нашел тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Несмотря на эти сомнения, математики уверенно применяли к комплексным числам привычные для вещественных величин алгебраические правила и получали корректные результаты[21].

Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным или вещественным результатам, или, например, извлечение корня может привести к открытию еще какого-то нового типа чисел. Задача о выражении корней степени из данного числа была решена в работах Муавра (1707) и Котса (1722)[23].

Символ для обозначения мнимой единицы предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву латинского слова imaginarius — «мнимый». Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль, что в системе комплексных чисел любой многочлен имеет корень (основная теорема алгебры, до Эйлера сходные предположения высказывали Альбер Жирар и Рене Декарт)[24]. К такому же выводу пришел д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799)[22]. Гаусс и ввел в широкое употребление термин «комплексное число» в 1831 году (ранее термин использовал в том же смысле французский математик Лазар Карно в 1803 году, но тогда он не получил распространения)[25].

Геометрическое представление комплексных чисел, немало способствовавшее их легализации, предложили в конце XVIII — начале XIX веков сначала Вессель и Арган (их работы не привлекли внимания), а затем Гаусс[26]. Арифметическая (стандартная) модель комплексных чисел как пар вещественных чисел была построена Гамильтоном («Теория алгебраических пар», 1837); это доказало непротиворечивость их свойств. Термины «модуль», «аргумент» и «сопряженное число» ввел в начале XIX века Коши, значительно продвинувший комплексный анализ. С XIX века началось бурное и чрезвычайно плодотворное развитие исследований функций комплексного переменного. [27].

С учетом этого успешного подхода начались поиски способа представления векторов в трехмерном пространстве, аналогичное комплексной плоскости. В результате пятнадцатилетних поисков Гамильтон предложил в 1843 году обобщение комплексных чисел — кватернионы, которые он был вынужден сделать не трехмерными, а четырехмерными (трехмерные векторы изображала мнимая часть кватернионов); также Гамильтону пришлось отказаться от коммутативности операции умножения .

В 1893 году Чарлз Штейнмец предложил использовать комплексные числа для расчетов электрических цепей переменного тока (см. ниже).

Комплексные функции

Аналитические функции

Комплексная функция одной переменной — это функция , которая определена на некоторой области комплексной плоскости и ставит в соответствие точкам этой области комплексные значения [28]. Примеры:

Каждая комплексная функция может рассматриваться как пара вещественных функций от двух переменных: , определяющих ее вещественную и мнимую часть соответственно. Функции

продолжение следует...

Продолжение:

Часть 1 Комплексные числа, определение и применение, операции над ними, физический смысл
Часть 2 Формы представления комплексного числа - Комплексные числа, определение и применение,
Часть 3 Место в общей алгебре, топологии и теории множеств - Комплексные
Часть 4 Вариации Обобщения и связанные с ними понятия - Комплексные числа,