Лекция
Привет, Вы узнаете о том , что такое взаимно обратные функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое взаимно обратные функции, обратные функции , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.
Пусть функция 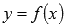 строго монотонная (возрастающая или убывающая) и непрерывная на области определения
строго монотонная (возрастающая или убывающая) и непрерывная на области определения 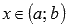 , область значений этой функции
, область значений этой функции 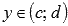 , тогда на интервале
, тогда на интервале 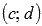 определена непрерывная строго монотонная функция
определена непрерывная строго монотонная функция 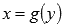 с областью значений
с областью значений 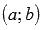 , которая является обратной для
, которая является обратной для 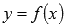 .
.
Другими словами, об обратной функции 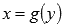 для функции
для функции 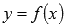 на конкретном промежутке имеет смысл говорить, если на этом интервале
на конкретном промежутке имеет смысл говорить, если на этом интервале 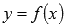 либо возрастает, либо убывает.
либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений 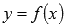 . Решения как раз и записываются через
обратные функции .
. Решения как раз и записываются через
обратные функции .
Например, требуется решить уравнение 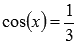 .
.
Решениями являются точки 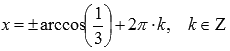 .
.
Функции косинус и арккосинус как раз являются обратными на области определения.
Рассмотрим несколько примеров нахождения обратных функций.
Начнем с линейных взаимнообратных функций.
Пример.
Найти функцию обратную для 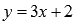 .
.
Решение.
Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение 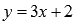 относительно x ).
относительно x ).
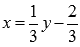 - это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать
- это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать 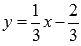 .
.
Таким образом, 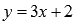 и
и 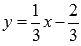 -
взаимно обратные функции .
-
взаимно обратные функции .
Приведем графическую иллюстрацию взаимно обратных линейных функций.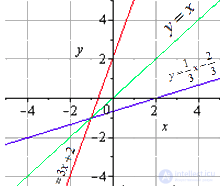
Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов). Это одно из свойств взаимно обратных функций, о которых речь пойдет ниже.
Теперь рассмотрим пример нахождения логарифмической функции, обратной к заданной показательной функции.
Пример.
Найти функцию обратную для 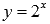 .
.
Решение.
Областью определения этой функции является все множество действительных чисел, областью значений является интервал 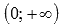 . Выразим x через y (другими словами, решим уравнение
. Выразим x через y (другими словами, решим уравнение 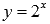 относительно x).
относительно x).
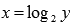 - это и есть обратная функция. Переставив буквы x и y , имеем
- это и есть обратная функция. Переставив буквы x и y , имеем 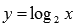 .
.
Таким образом, 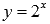 и
и 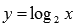 - показательная и логарифмическая функции есть взаимно обратные функции на области определения.
- показательная и логарифмическая функции есть взаимно обратные функции на области определения.
График взаимно обратных показательной и логарифмической функций.
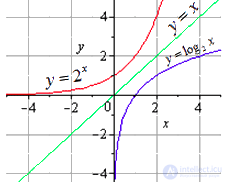
Перечислим свойства взаимно обратных функций 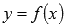 и
и 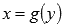 .
.
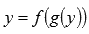 и
и 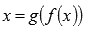 .
.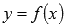 совпадает с областью значений функции
совпадает с областью значений функции 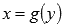 и наоборот.
и наоборот.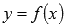 возрастает, то и
возрастает, то и 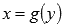 возрастает, если
возрастает, если 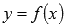 убывает, то и
убывает, то и 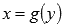 убывает.
убывает.Замечание по свойству 1).
Рекомендуем ОЧЕНЬ ВНИМАТЕЛЬНО относиться к области определения и области значений функций.
Например: 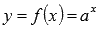 и
и 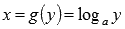 - взаимно обратные функции. По первому свойству имеем
- взаимно обратные функции. По первому свойству имеем 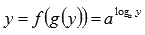 . Это равенство верно только для положительных y , для отрицательных y логарифм не определен. Так что не спешите с записями вида
. Это равенство верно только для положительных y , для отрицательных y логарифм не определен. Так что не спешите с записями вида 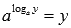 , а если уж так написали, то следует добавить фразу «при положительных y».
, а если уж так написали, то следует добавить фразу «при положительных y».
Равенство 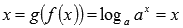 в свою очередь верно для любых действительных x.
в свою очередь верно для любых действительных x.
Надеемся, Вы уловили этот тонкий момент.
Особенно аккуратными надо быть с тригонометрическими и обратными тригонометрическими функциями.
К примеру, 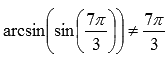 , так как область значений арксинуса
, так как область значений арксинуса 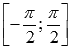 , а
, а 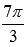 в нее не попадает.
в нее не попадает.
Правильно будет
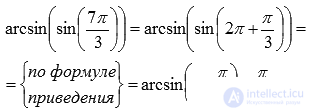
В свою очередь 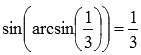 есть верное равенство.
есть верное равенство.
То есть 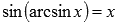 при
при 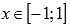 и
и 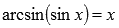 при
при 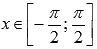 .
.
Еще раз подчеркнем: БУДЬТЕ ВНИМАТЕЛЬНЫ С ОБЛАСТЬЮ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЮ ЗНАЧЕНИЙ!
Взаимно обратные степенные функции, графики.
Для степенной функции 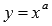 при
при 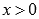 обратной является также степенная функция
обратной является также степенная функция 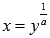 Если заменить буквы, то получим пару взаимно обратных функций
Если заменить буквы, то получим пару взаимно обратных функций 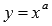 и
и 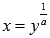
Графики для положительных а и отрицательных а.
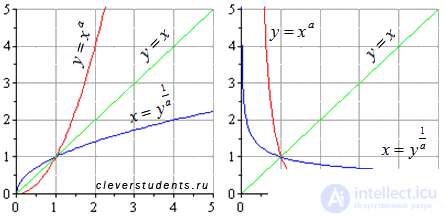
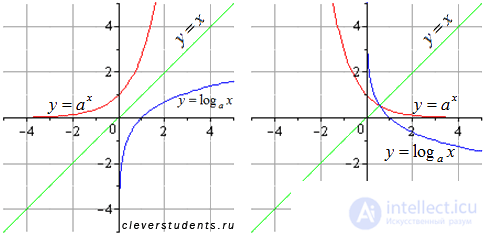
Взаимно обратные показательная и логарифмическая функции 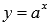 и
и 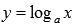 , графики.
, графики.
Подразумеваем, что а положительное и не равное единице число.
Графики для 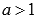 и для
и для 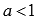
Взаимно обратные тригонометрические и обратные тригонометрические функции.
График главной ветви синуса и арксинуса (светлая область).
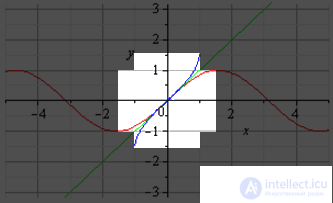
График главной ветви косинуса и арккосинуса (светлая область).
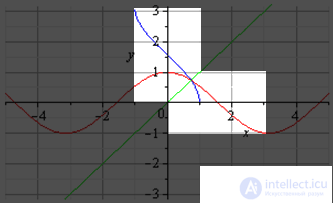
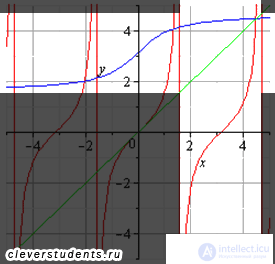
График главной ветви тангенса и арктангенса (светлая область).
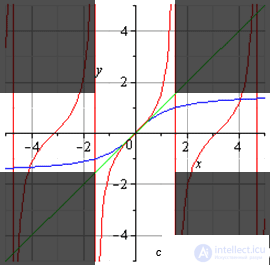
График главной ветви котангенса и арккотангенса (светлая область).
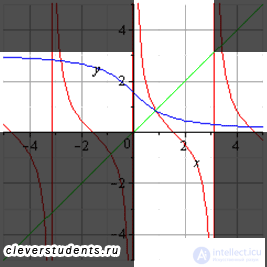
Если Вам потребуются обратные функции для ветвей тригонометрических функций, отличных от главных, то соответствующую обратную тригонометрическую функцию нужно будет сдвинуть вдоль оси ординат на необходимое количество периодов.
Например, если Вам потребуется обратная функция для ветви тангенса на промежутке 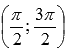 (эта ветвь получается из главной ветви сдвигом на величину
(эта ветвь получается из главной ветви сдвигом на величину 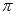 вдоль оси ох ), то ей будет являться ветвь арктангенса, сдвинутая вдоль оси oy на
вдоль оси ох ), то ей будет являться ветвь арктангенса, сдвинутая вдоль оси oy на 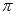 .
.
Пока на этом закончим с обратными функциями.
Не следует путать с Обратная величина.
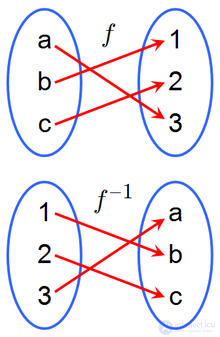
Функция и обратная ей функция
. Об этом говорит сайт https://intellect.icu . Если
, то
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x дает y, то обратная ей функция от y дает x. Обратная функция функции обычно обозначается
, иногда также используется обозначение
.
Функция, имеющая обратную, называется обратимой.
Функция называется обратной к функции
, если выполнены следующие тождества:
Чтобы найти обратную функцию, нужно решить уравнение относительно
. Если оно имеет более чем один корень, то функции, обратной к
не существует. Таким образом, функция
обратима на интервале
тогда и только тогда, когда на этом интервале она взаимно-однозначна.
Для непрерывной функции выразить
из уравнения
возможно в том и только том случае, когда функция
строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках ее строгой монотонности. Например,
является обратной функцией к
на
, хотя на промежутке
обратная функция другая:
.
Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция где
— функция Дирихле, разрывна и не монотонна, однако обратная для нее существует :
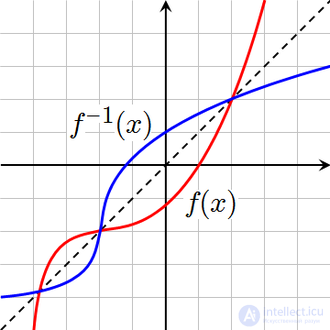
Графики функции и обратной ей
или
,
,
или короче
,
,
где {\displaystyle \circ } означает композицию функций, а
— тождественные отображения на
и
соответственно.
.
Обратная функция аналитической в некоторой окрестности точки функции может быть представлена в виде степенного ряда:
где функции задаются рекурсивной формулой:
Исследование, описанное в статье про взаимно обратные функции, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое взаимно обратные функции, обратные функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Из статьи мы узнали кратко, но содержательно про взаимно обратные функции
Комментарии
Оставить комментарий
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Термины: СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА