Лекция
Game: Perform tasks and rest cool.2 people play!
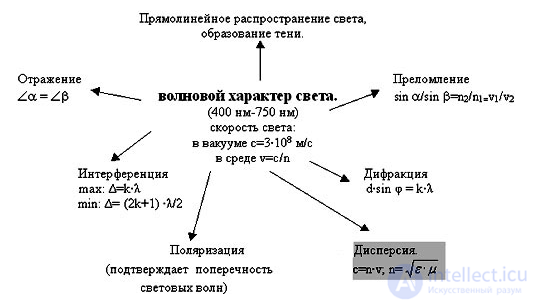
Play gameПривет, Вы узнаете о том , что такое поглощение света, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое поглощение света, рассеяние света, дисперсия света, поляризация света, опалесценция , настоятельно рекомендую прочитать все из категории Колебания и волны (Оптика, акустика и радиофизика).
В этом разделе мы рассмотрим некоторые эффекты, возникающие при распространении света в среде. Первый из них — поляризация — связан с поперечной анизотропией световых волн, то есть с неэквивалентностью различных направлений в плоскости, перпендикулярной световому лучу. Далее мы проанализируем явление дисперсии света, которое проявляется в зависимости фазовой скорости распространения световых волн в среде от частоты (длины волны). Наконец, мы коротко остановимся на поглощении и рассеянии света в сред.
Следствием теории Максвелла является поперечность электромагнитных (световых) волн распространяющихся в вакууме или изотропной среде: векторы напряженности электрического и магнитного полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны (то есть перпендикулярно световому лучу). Явление поляризации света служит надежным обоснованием поперечности световой волны. При рассмотрении поляризации обычно все рассуждения связывают с плоскостью колебаний вектора напряженности электрического поля Е — светового вектора, так как химическое, физиологическое и другие виды воздействия света на вещество обусловлены главным образом электрическими колебаниями. Однако при этом следует помнить об обязательном существовании перпендикулярного ему вектора напряженности магнитного поля Н.
Поляризация электромагнитной волны. Записывая решение для электрического поля плоской электромагнитной волны в виде
|
|
|
(6.1) |
мы предполагали, что направление вектора амплитуды колебаний 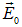 не зависит от времени. В этом случае вектор электрического поля всегда и во всех точках волны направлен вдоль одной и той же прямой — колеблется в одной плоскости неизменной ориентации в пространстве.
не зависит от времени. В этом случае вектор электрического поля всегда и во всех точках волны направлен вдоль одной и той же прямой — колеблется в одной плоскости неизменной ориентации в пространстве.
|
Плоскость, в которой происходят колебания светового вектора, то есть плоскость, содержащая вектор |
Game: Perform tasks and rest cool.2 people play!
Play game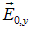 , записываем (6.1) в виде
, записываем (6.1) в виде
|
|
|
(6.2) |
Однако существует и вторая линейно поляризованная волна, имеющая ту же частоту и распространяющаяся в том же направлении:
|
|
|
(6.3) |
Game: Perform tasks and rest cool.2 people play!
Play game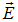 будет описывать эллиптическую, в общем случае, траекторию в плоскости, параллельной y0z. Вращение вектора
будет описывать эллиптическую, в общем случае, траекторию в плоскости, параллельной y0z. Вращение вектора 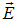 происходит с частотой волны
происходит с частотой волны 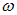 . В этом случае говорят, что свет имеет эллиптическую поляризацию. Если разность фаз
. В этом случае говорят, что свет имеет эллиптическую поляризацию. Если разность фаз 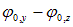 кратна
кратна 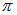 , то эллиптическая поляризация вырождается в линейную. При равенстве амплитуд Е0,у и Е0,г эллипс превращается в окружность. Тогда говорят о круговой поляризации волны. В соответствии с двумя возможными направлениями вращения вектора
, то эллиптическая поляризация вырождается в линейную. При равенстве амплитуд Е0,у и Е0,г эллипс превращается в окружность. Тогда говорят о круговой поляризации волны. В соответствии с двумя возможными направлениями вращения вектора 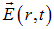 возможны право- и левополяризованные волны. Любую электромагнитную волну можно представить как линейную комбинацию двух линейно поляризованных волн или как линейную комбинацию двух волн с круговой поляризацией. Иными словами, электромагнитные волны имеют две внутренние степени свободы.
возможны право- и левополяризованные волны. Любую электромагнитную волну можно представить как линейную комбинацию двух линейно поляризованных волн или как линейную комбинацию двух волн с круговой поляризацией. Иными словами, электромагнитные волны имеют две внутренние степени свободы.
Естественный и поляризованный свет. В свете, испускаемом обычными источниками, имеются колебания, совершающиеся в различных направлениях, перпендикулярных к лучу. В таких световых волнах, исходящих из различных элементарных излучателей (атомов), векторы 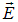 имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным.
имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным.
Если под влиянием внешних воздействий на свет или внутренних особенностей источника света (лазер) появляется предпочтительное, наиболее вероятное направление колебаний, то такой свет называется частично поляризованным. Неполяризованный (естественный) свет может испускаться лишь огромным числом элементарных излучателей. Электромагнитная волна от отдельного элементарного излучателя (атома, молекулы) всегда поляризована. С помощью различных поляризаторов из пучка естественного света можно выделить часть, в которой колебания вектора 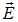 будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, то есть выделенный свет будет линейно поляризованным.
будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, то есть выделенный свет будет линейно поляризованным.
На рисунках направление колебаний электрического поля линейно поляризованной волны изображается следующим образом. Если вектор Е колеблется в плоскости чертежа, то на направление вектора скорости волны 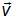 наносится ряд вертикальных стрелочек (рис. 6.1-1), а если в плоскости, перпендикулярной чертежу, — ряд точек (рис. 6.1-2). Естественный (неполяризованный) свет условно обозначается чередующимися черточками, которым соответствует, например, компонента Еy вектора напряженности электрического поля, и точками, соответствующими другой компоненте Еz (рис. 6.1-3).
наносится ряд вертикальных стрелочек (рис. 6.1-1), а если в плоскости, перпендикулярной чертежу, — ряд точек (рис. 6.1-2). Естественный (неполяризованный) свет условно обозначается чередующимися черточками, которым соответствует, например, компонента Еy вектора напряженности электрического поля, и точками, соответствующими другой компоненте Еz (рис. 6.1-3).
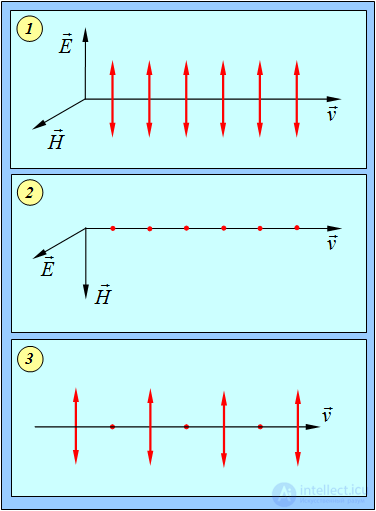
Рис. 6.1. Условные обозначения типа поляризации волны
Существуют приборы (поляризаторы), пропускающие только колебания, происходящие параллельно некоторой плоскости, называемой плоскостью поляризации прибора, и полностью задерживающие ортогональные колебания. Если пропустить через такой прибор пучок света, то на выходе он будет линейно поляризованным. При вращении прибора вокруг направления луча интенсивность выходящего света будет изменяться от IMAX до IMIN.
Game: Perform tasks and rest cool.2 people play!
Play game|
Степень поляризации света — это величина
|
Отметим, что формула (6.4) пригодна для расчета степени поляризации света лишь в том случае, когда частично поляризованный свет представляет собой смесь естественного света и света линейно поляризованного и не работает, например, в случае смеси естественного света и света поляризованного по кругу. В общем случае степень поляризации может быть рассчитана как отношение интенсивности поляризованной компоненты 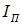 к суммарной интенсивности волны, то есть сумме интенсивностей поляризованной
к суммарной интенсивности волны, то есть сумме интенсивностей поляризованной 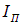 и естественной
и естественной 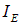 компонент смеси:
компонент смеси:
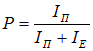
Нетрудно показать, что (6.4) есть частный случай последней формулы.
Если падающий пучок света линейно поляризован, то при положении прибора, когда его плоскость поляризации ортогональна плоскости колебаний волны, свет через прибор не пройдет, то есть 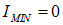 . В соответствии с формулой (6.4) степень поляризации такого света
. В соответствии с формулой (6.4) степень поляризации такого света 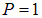 . Для частично поляризованного света
. Для частично поляризованного света
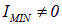
Game: Perform tasks and rest cool.2 people play!
Play game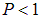 . Для естественного света, где волны разных поляризаций смешаны в равной степени и все направления эквивалентны, интенсивность выходящего света не изменяется при вращении поляризатора, так что
. Для естественного света, где волны разных поляризаций смешаны в равной степени и все направления эквивалентны, интенсивность выходящего света не изменяется при вращении поляризатора, так что 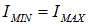 и
и 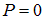 .
.
Закон Малюса. В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например природные кристаллы турмалина. Монокристалл турмалина поглощает колебания вектора Е в одном направлении настолько сильно, что сквозь пластинку толщиной порядка 1 мм проходит только линейно поляризованный луч. Кристаллы йодистого хинина еще сильнее поглощают одну из поляризаций: кристаллическая пленка толщиной в десятую долю миллиметра практически полностью отделяет один из линейно поляризованных лучей.
Пусть естественный свет распространяется перпендикулярно плоскости рисунка 6.2.
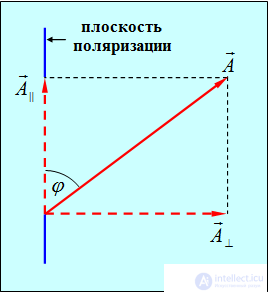
Рис. 6.2. Разложение вектора амплитуды колебаний А в волне, падающей на поляризатор
Вектор 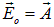 амплитуды колебаний электрического поля волны, совершающихся в плоскости, образующей с плоскостью поляризатора угол
амплитуды колебаний электрического поля волны, совершающихся в плоскости, образующей с плоскостью поляризатора угол 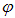 , можно разложить на два колебания с амплитудами
, можно разложить на два колебания с амплитудами
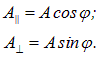
Первое колебание с амплитудой А|| пройдет через прибор (поляризатор), второе — с амплитудой А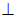 — будет задержано (поглощено). Интенсивность прошедшей волны пропорциональна квадрату амплитуды
— будет задержано (поглощено). Интенсивность прошедшей волны пропорциональна квадрату амплитуды
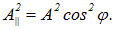
Падающая волна является смесью волн с различными углами 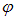 . Усредняя по углам, получаем для интенсивности света на выходе из поляризатора:
. Усредняя по углам, получаем для интенсивности света на выходе из поляризатора:
|
|
|
(6.5) |
где 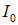 — интенсивность падающего на поляризатор света. В естественном свете все значения угла
— интенсивность падающего на поляризатор света. В естественном свете все значения угла 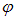 равновероятны:
равновероятны:
Game: Perform tasks and rest cool.2 people play!
Play game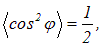
так что интенсивность света, прошедшего через поляризатор, будет равна 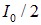 . При вращении поляризатора вокруг направления луча естественного света интенсивность прошедшего света остается неизменной, но изменяется лишь ориентация плоскости колебаний света, выходящего из прибора.
. При вращении поляризатора вокруг направления луча естественного света интенсивность прошедшего света остается неизменной, но изменяется лишь ориентация плоскости колебаний света, выходящего из прибора.
Рассмотрим теперь падение линейно поляризованного света с интенсивностью 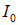 на тот же поляризатор (рис. 6.3).
на тот же поляризатор (рис. 6.3).
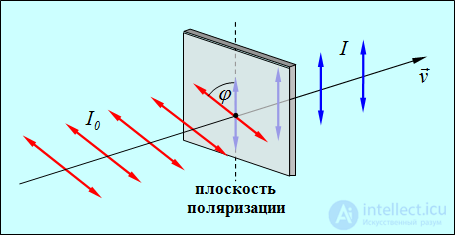
Рис. 6.3. Прохождение линейно поляризованной волны через поляризатор
Видео 6.1 Поляризатор и анализатор для дециметровой волны.
Видео 6.2 Поляризатор и анализатор для трехсантиметровой волны.
Сквозь прибор пройдет составляющая колебаний с амплитудой
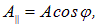
Game: Perform tasks and rest cool.2 people play!
Play game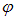 — угол между плоскостью колебаний вектора Е и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением
— угол между плоскостью колебаний вектора Е и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением
|
|
|
(6.6) |
которое носит название закона Малюса.
Видео 6.3 Поляризатор и анализатор для видимого света — 2
Видео 6.4 Естественный видимый свет. Три поляризатора. Закон Малюса.
Поляризационные приборы по своему целевому назначению делятся на поляризаторы и анализаторы. Поляризаторы служат для получения поляризованного света. С помощью анализатора можно убедиться, что падающий свет поляризован, и выяснить направление плоскости поляризации. Принципиальных различий в конструкционном отношении между поляризатором и анализатором не существует.
Поставим на пути естественного света два поляризатора, плоскости которых образуют угол 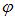 (рис. 6.4).
(рис. 6.4).
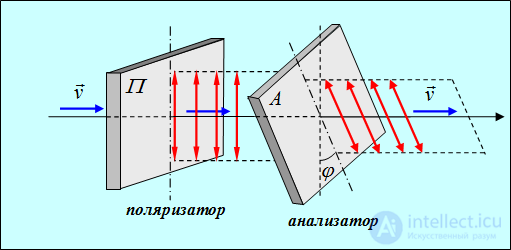
Рис. 6.4. Пропускание естественного света через систему из двух поляризаторов
Из первого поляризатора выйдет линейно поляризованный свет, интенсивность которого 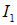 , составит половину интенсивности падающего естественного света
, составит половину интенсивности падающего естественного света 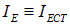 . Согласно закону Малюса из второго поляризатора (который играет роль анализатора) выйдет свет с интенсивностью
. Согласно закону Малюса из второго поляризатора (который играет роль анализатора) выйдет свет с интенсивностью
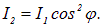
Таким образом, интенсивность света, прошедшего через два поляризатора, равна
|
|
|
(6.7) |
Если угол 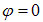 (плоскости поляризации поляризатора и анализатора параллельны), то
(плоскости поляризации поляризатора и анализатора параллельны), то 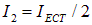 ; если
; если 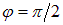 (анализатор и поляризатор скрещены), то
(анализатор и поляризатор скрещены), то 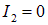 .
.
Game: Perform tasks and rest cool.2 people play!
Play gameПоскольку интенсивность пропорциональна квадрату амплитуды, имеем
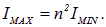
Отсюда степень поляризации света равна
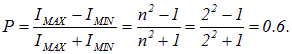
Пример 2. На пути света со степенью поляризации Р = 0.6 поставили анализатор так, что интенсивность прошедшего света стала максимальной. Определим, во сколько раз уменьшится интенсивность, если анализатор повернуть на угол 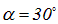 ?
?
В падающем луче по условию (см. предыдущий пример)
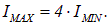
При повороте анализатора на угол 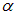 будут пропущены колебания, параллельные плоскости поляризации прибора. Поэтому интенсивность пропущенных колебаний, прежде бывших параллельными плоскости поляризации, составит
будут пропущены колебания, параллельные плоскости поляризации прибора. Поэтому интенсивность пропущенных колебаний, прежде бывших параллельными плоскости поляризации, составит
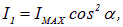
Game: Perform tasks and rest cool.2 people play!
Play game
Суммарная интенсивность прошедших колебаний равна сумме
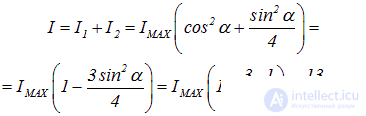
Стало быть, интенсивность уменьшится при повороте анализатора в 16/13 = 1.23 раза.
Поляризация при отражении и преломлении. Получить поляризованный свет из естественного можно еще одним способом — отражением. Опыт показывает, что отраженный от поверхности диэлектрика и преломленный лучи всегда частично поляризованы. Когда свет падает на диэлектрическую поверхность, то в отраженном луче преобладают колебания, перпендикулярные плоскости падения (точки на рис. 6.5), а в преломленном луче - колебания, параллельные плоскости падения (стрелки на рис. 6.5).
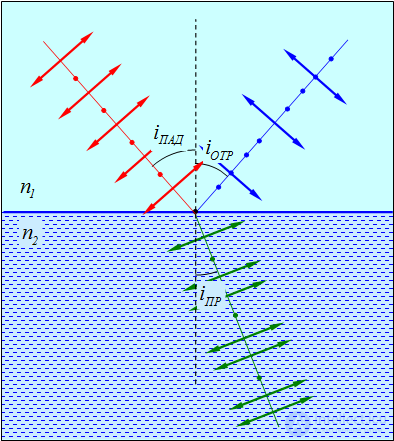
Рис. Об этом говорит сайт https://intellect.icu . 6.5. Поляризация света при отражении и преломлении
Видео 6.5 Поляризация естественного света при отражении от стекла.
Степень поляризации зависит от угла падения лучей и от относительного показателя преломления сред. Исследуя это явление, английский физик Д. Брюстер установил, что при определенном значении угла падения
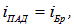
удовлетворяющем условию
|
|
|
(6.8) |
отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча. Это соотношение известно как закон Брюстера. При
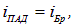
отражается только та компонента вектора напряженности электрического поля, которая параллельна поверхности диэлектрика (перпендикулярна плоскости падения). Соответственно, преломленный луч всегда частично поляризован, так как отражается лишь какая-то доля падающего света (не равная 50 %).
Game: Perform tasks and rest cool.2 people play!
Play game|
При падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны, отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча, а преломленный луч частично поляризован с максимальной степенью поляризации. |
Видео 6.6 Угол Брюстера.
Действительно, при
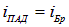
находим с учетом закона преломления
|
|
|
(6.10) |
Получаем отсюда
Game: Perform tasks and rest cool.2 people play!
Play game|
|
|
(6.11) |
Таким образом,
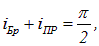
откуда следует, что преломленный луч 0С перпендикулярен отраженному лучу 0В (рис. 6.6).
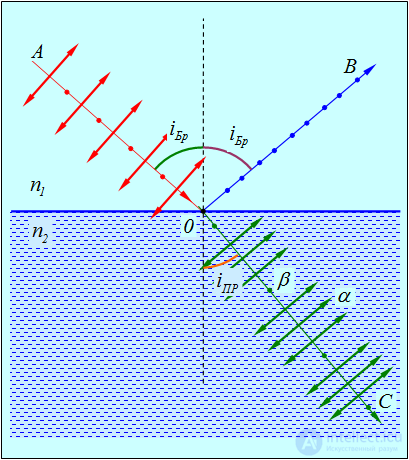
Рис.6.6. Ход лучей при падении света под углом Брюстера: отраженный луч ортогонален преломленному,
поэтому излучатели типа  (см. текст ниже) не вносят вклад в поляризацию отраженного луча
(см. текст ниже) не вносят вклад в поляризацию отраженного луча
Для того чтобы объяснить, почему отраженный при падении под углом Брюстера луч линейно поляризован в плоскости, перпендикулярной плоскости падения, учтем, что отраженный свет есть результат излучения вторичных волн колеблющимися под действием светового вектора волны электрическими зарядами (электронами) в среде II. Эти колебания происходят в направлении колебаний вектора Е.
Разложим колебания вектора Е в среде II на два взаимно перпендикулярных направления (см. рис. 6.6): колебания  , происходящие в плоскости падения (показаны стрелками), и колебания
, происходящие в плоскости падения (показаны стрелками), и колебания  , происходящие перпендикулярно плоскости падения (показаны точками). В случае падения под углом Брюстера
, происходящие перпендикулярно плоскости падения (показаны точками). В случае падения под углом Брюстера
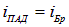
отраженный луч 0В перпендикулярен преломленному лучу 0С. Следовательно, 0В параллелен  . Из электромагнитной теории Максвелла известно, что колеблющийся электрический заряд не излучает электромагнитных волн вдоль направления своего движения. Поэтому колеблющийся в диэлектрике излучатель типа
. Из электромагнитной теории Максвелла известно, что колеблющийся электрический заряд не излучает электромагнитных волн вдоль направления своего движения. Поэтому колеблющийся в диэлектрике излучатель типа 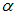 вдоль направления 0В не излучает. Таким образом, по направлению отраженного луча 0В распространяется свет, посылаемый только излучателями типа
вдоль направления 0В не излучает. Таким образом, по направлению отраженного луча 0В распространяется свет, посылаемый только излучателями типа 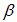 , направления колебаний которых перпендикулярны плоскости падения.
, направления колебаний которых перпендикулярны плоскости падения.
Следует отметить, что на опыте закон Брюстера не выполняется вполне строго из-за дисперсии света.
Пример 3. Определим, на какой угловой высоте 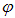 над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован.
над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован.
Угол падения света связан с высотой Солнца над горизонтом соотношением
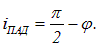
По условию угол падения равен углу Брюстера, так что
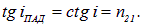
Показатели преломления воды п2 = 1.33, воздуха — п1 = 1. Отсюда находим
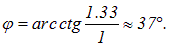
Game: Perform tasks and rest cool.2 people play!
Play game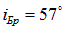 . Определим скорость света V в этом кристалле.
. Определим скорость света V в этом кристалле.
Поскольку показатель преломления воздуха равен единице, показатель преломления каменной соли п совпадает с относительным показателем преломления 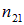 этих двух сред. Имеем поэтому
этих двух сред. Имеем поэтому
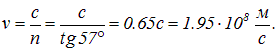
Game: Perform tasks and rest cool.2 people play!
Play game|
Дисперсия света — это зависимость показателя преломления n вещества от длины волны света (в вакууме)
|
или, что то же самое, зависимость фазовой скорости световых волн от частоты:
|
|
|
(6.13) |
|
Дисперсией вещества называется производная от n по
|
Дисперсия — зависимость показателя преломления вещества от частоты волны – особенно ярко и красиво проявляет себя совместно с эффектом двойного лучепреломления (см. Видео 6.6 в предыдущем параграфе), наблюдаемом при прохождении света через анизотропные вещества. Дело в том, что показатели преломления обыкновенной и необыкновенной волн различно зависят от частоты волны. В результате цвет (частота) света прошедшего через анизотропное вещество помещенное между двумя поляризаторами зависит как от толщины слоя этого вещества, так и от угла между плоскостями пропускания поляризаторов.
Видео 6.8 Дисперсия и анизотропия: пластинки слюды между поляризаторами.
Видео 6.9 Дисперсия и анизотропия: полимерная пленка между поляризаторами.
Видео 6.10 Дисперсия и анизотропия: болванка CD-диска.
Видео 6.11 Дисперсия и анизотропия: нагруженная «балка».
Видео 6.12 Дисперсия и анизотропия: мятая целлофановая обертка.
Видео 6.13 Дисперсия и анизотропия: слюдяная бабочка и…
Для всех прозрачных бесцветных веществ в видимой части спектра с уменьшением длины волны показатель преломления увеличивается, то есть дисперсия вещества отрицательна: 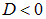 . (рис. 6.7, области 1-2, 3-4)
. (рис. 6.7, области 1-2, 3-4)
|
Нормальная дисперсия вещества — это отрицательная дисперсия
|
Если вещество поглощает свет в каком-то диапазоне длин волн (частот), то в области поглощения дисперсия
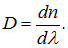
оказывается положительной и называется аномальной (рис. 6.7, область 2–3).
Game: Perform tasks and rest cool.2 people play!
Play game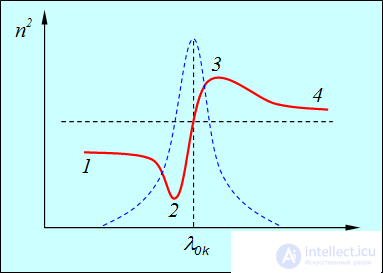
Рис. 6.7. Зависимость квадрата показателя преломления (сплошная кривая) и коэффициента поглощения света веществом
(штриховая кривая) от длины волны l вблизи одной из полос поглощения ( )
)
Изучением нормальной дисперсии занимался еще Ньютон. Разложение белого света в спектр при прохождении сквозь призму является следствием дисперсии света. При прохождении пучка белого света через стеклянную призму на экране возникает разноцветный спектр (рис. 6.8).
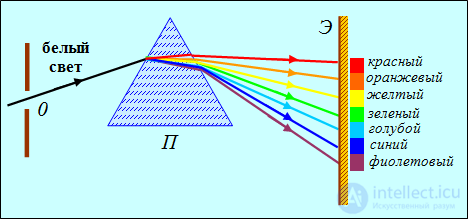
Рис. 6.8. Прохождение белого света через призму: вследствие различия значений показателя преломления стекла для разных
длин волн пучок разлагается на монохроматические составляющие — на экране возникает спектр
Наибольшую длину волны и наименьший показатель преломления имеет красный свет, поэтому красные лучи отклоняются призмой меньше других. Рядом с ними будут лучи оранжевого, потом желтого, зеленого, голубого, синего и, наконец, фиолетового света. Произошло разложение падающего на призму сложного белого света на монохроматические составляющие (спектр).
Ярким примером дисперсии является радуга. Радуга наблюдается, если солнце находится за спиной наблюдателя. Красные и фиолетовые лучи преломляются сферическими капельками воды и отражаются от их внутренней поверхности. Красные лучи преломляются меньше и попадают в глаз наблюдателя от капелек, находящихся на большей высоте. Поэтому верхняя полоса радуги всегда оказывается красной (рис. 26.8).
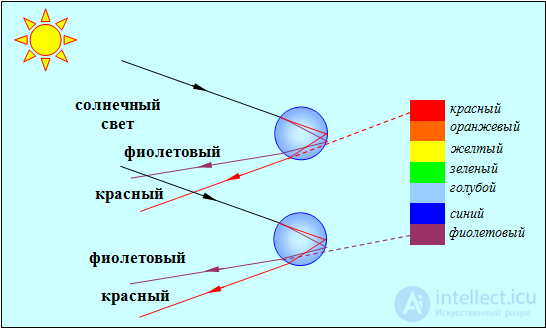
Рис. 6.9. Возникновение радуги
Используя законы отражения и преломления света, можно рассчитать ход световых лучей при полном отражении и дисперсии в дождевых каплях. Оказывается, что лучи рассеиваются с наибольшей интенсивностью в направлении, образующем угол около 42° с направлением солнечных лучей (рис. 6.10).
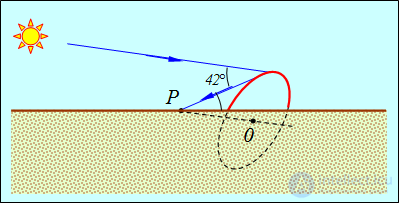
Рис. 6.10. Расположение радуги
Геометрическое место таких точек представляет собой окружность с центром в точке 0. Часть ее скрыта от наблюдателя Р под горизонтом, дуга над горизонтом и есть видимая радуга. Возможно также двойное отражение лучей в дождевых каплях, приводящее к радуге второго порядка, яркость которой, естественно, меньше яркости основной радуги. Для нее теория дает угол 51°, то есть радуга второго порядка лежит вне основной. В ней порядок цветов заменен на обратный: внешняя дуга окрашена в фиолетовый цвет, а нижняя — в красный. Радуги третьего и высших порядков наблюдаются редко.
Элементарная теория дисперсии. Зависимость показателя преломления вещества от длины электромагнитной волны (частоты) объясняется на основе теории вынужденных колебаний. Строго говоря, движение электронов в атоме (молекуле) подчиняется законам квантовой механики. Однако для качественного понимания оптических явлений можно ограничиться представлением об электронах, связанных в атоме (молекуле) упругой силой. При отклонении от равновесного положения такие электроны начинают колебаться, постепенно теряя энергию на излучение электромагнитных волн или передавая свою энергию узлам решетки и нагревая вещество. В результате этого колебания будут затухающими.
При прохождении через вещество электромагнитная волна воздействует на каждый электрон с силой Лоренца:
|
|
|
(6.15) |
где v — скорость колеблющегося электрона. В электромагнитной волне отношение напряженностей магнитного и электрического полей равно
|
|
|
(6.16) |
Поэтому нетрудно оценить отношение электрической и магнитной сил, действующих на электрон:
|
|
|
(6.17) |
Game: Perform tasks and rest cool.2 people play!
Play game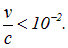
Таким образом, можно считать, что при прохождении через вещество электромагнитной волны на каждый электрон действует только электрическая сила:
|
|
|
(6.18) |
где 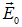 — амплитуда напряженности электрического поля в световой волне,
— амплитуда напряженности электрического поля в световой волне,  — фаза волны, определяемая положением рассматриваемого электрона. Для упрощения вычислений пренебрежем затуханием и запишем уравнение движения электрона в виде
— фаза волны, определяемая положением рассматриваемого электрона. Для упрощения вычислений пренебрежем затуханием и запишем уравнение движения электрона в виде
|
|
|
(6.19) |
где, 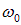 — собственная частота колебаний электрона в атоме. Решение такого дифференциального неоднородного уравнения мы уже рассматривали ранее и получили
— собственная частота колебаний электрона в атоме. Решение такого дифференциального неоднородного уравнения мы уже рассматривали ранее и получили
|
|
|
(6.20) |
Следовательно, смещение электрона из положения равновесия пропорционально напряженности электрического поля. Смещениями ядер из положения равновесия можно пренебречь, так как массы ядер весьма велики по сравнению с массой электрона.
Атом со смещенным электроном приобретает дипольный момент
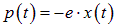
(для простоты положим пока, что в атоме имеется только один «оптический» электрон, смещение которого вносит определяющий вклад в поляризацию). Если в единице объема содержится N атомов, то поляризованность среды (дипольный момент единицы объема) можно записать в виде
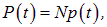
|
|
|
(6.21) |
В реальных средах возможны разные типы колебаний зарядов (групп электронов или ионов), вносящих вклад в поляризацию. Эти типы колебаний могут иметь разные величины заряда еi и массы тi, а также различные собственные частоты 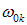 (мы будем обозначать их индексом k), при этом число атомов в единице объема с данным типом колебаний Nk пропорционально концентрации атомов N:
(мы будем обозначать их индексом k), при этом число атомов в единице объема с данным типом колебаний Nk пропорционально концентрации атомов N:
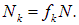
Безразмерный коэффициент пропорциональности fk характеризует эффективный вклад каждого типа колебаний в общую величину поляризации среды:
|
|
|
(6.22) |
С другой стороны, как известно,
|
|
|
(6.23) |
где 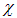 — диэлектрическая восприимчивость вещества, которая связана с диэлектрической проницаемостью e соотношением
— диэлектрическая восприимчивость вещества, которая связана с диэлектрической проницаемостью e соотношением
Game: Perform tasks and rest cool.2 people play!
Play game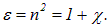
В результате получаем выражение для квадрата показателя преломления вещества:
|
|
|
(6.24) |
Вблизи каждой из собственных частот 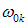 функция
функция 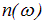 , определяемая формулой (6.24), терпит разрыв. Такое поведение показателя преломления обусловлено тем, что мы пренебрегли затуханием. Аналогично, как мы видели ранее, пренебрежение затуханием приводит к бесконечному росту амплитуды вынужденных колебаний при резонансе. Учет затухания избавляет нас от бесконечностей, и функция
, определяемая формулой (6.24), терпит разрыв. Такое поведение показателя преломления обусловлено тем, что мы пренебрегли затуханием. Аналогично, как мы видели ранее, пренебрежение затуханием приводит к бесконечному росту амплитуды вынужденных колебаний при резонансе. Учет затухания избавляет нас от бесконечностей, и функция 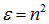 имеет вид, изображенный на рис. 6.11.
имеет вид, изображенный на рис. 6.11.
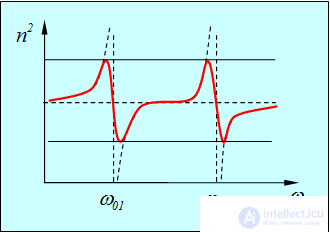
Рис. 6.11. Зависимость диэлектрической проницаемости среды 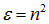 от частоты электромагнитной волны
от частоты электромагнитной волны
Учитывая связь частоты с длиной электромагнитной волны в вакууме 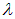
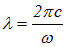
или
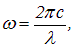
можно получить зависимость показателя преломления вещества п от длины волны в области нормальной дисперсии (участки 1–2 и 3–4 на рис. 6.7):
|
|
|
(6.25) |
где
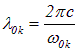
— длины волн, соответствующие собственным частотам колебаний 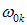 ,
, 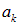 — постоянные коэффициенты.
— постоянные коэффициенты.
В области аномальной дисперсии (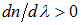 ) частота внешнего электромагнитного поля близка к одной из собственных частот колебаний молекулярных диполей, то есть возникает резонанс. Именно в этих областях (например, участок 2–3 на рис. 6.7) наблюдается существенное поглощение электромагнитных волн; коэффициент поглощения света веществом показан штриховой линией на рис. 6.7.
) частота внешнего электромагнитного поля близка к одной из собственных частот колебаний молекулярных диполей, то есть возникает резонанс. Именно в этих областях (например, участок 2–3 на рис. 6.7) наблюдается существенное поглощение электромагнитных волн; коэффициент поглощения света веществом показан штриховой линией на рис. 6.7.
Понятие о групповой скорости. С явлением дисперсии тесно связано понятие о групповой скорости. При распространении в среде с дисперсией реальных электромагнитных импульсов, например известных нам цугов волн, испускаемых отдельными атомными излучателями, происходит их «расплывание» — расширение протяженности в пространстве и длительности во времени. Это связано с тем, что такие импульсы представляют собой не монохроматическую синусоидальную волну, а так называемый волновой пакет, или группу волн — совокупность гармонических составляющих с разными частотами 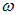 и с разными амплитудами, каждая из которых распространяется в среде со своей фазовой скоростью (6.13).
и с разными амплитудами, каждая из которых распространяется в среде со своей фазовой скоростью (6.13).
Если бы волновой пакет распространялся в вакууме, то его форма и пространственно-временная протяженность оставались бы неизменными, а скоростью распространения такого цуга волн была бы фазовая скорость света в вакууме
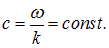
Из-за наличия дисперсии зависимость частоты электромагнитной волны от волнового числа k становится нелинейной, и скорость распространения цуга волн в среде, то есть скорость переноса энергии, определяется производной
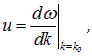
где 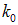 — волновое число для «центральной» волны в цуге (обладающей наибольшей амплитудой).
— волновое число для «центральной» волны в цуге (обладающей наибольшей амплитудой).
Game: Perform tasks and rest cool.2 people play!
Play game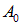 и начальными фазами
и начальными фазами 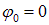 , но различающихся частотами, сдвинутыми относительно «центральной» частоты
, но различающихся частотами, сдвинутыми относительно «центральной» частоты 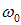 на небольшую величину
на небольшую величину 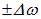 . Соответствующие волновые числа сдвинуты относительно «центрального» волнового числа
. Соответствующие волновые числа сдвинуты относительно «центрального» волнового числа 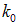 на небольшую величину
на небольшую величину 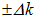 . Эти волны описываются выражениями:
. Эти волны описываются выражениями:
|
|
|
(6.26) |
Для результирующей волны
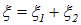
после применения тригонометрической формулы для суммы двух косинусов получим выражение:
|
|
|
(6.27) |
Мы убеждаемся, что результирующую волну можно представить как плоскую волну с «центральными» частотой 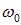 и волновым числом
и волновым числом 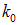 , амплитуда которой A(t) есть медленно меняющаяся (в силу малости сдвигов
, амплитуда которой A(t) есть медленно меняющаяся (в силу малости сдвигов 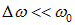 и
и 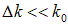 ) функция времени и координаты. Похожий результат ранее был получен при изучении биений. Видно, что сама эта переменная амплитуда есть плоская волна, распространяющаяся со скоростью
) функция времени и координаты. Похожий результат ранее был получен при изучении биений. Видно, что сама эта переменная амплитуда есть плоская волна, распространяющаяся со скоростью
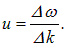
В пределе бесконечно малых сдвигов частоты приходим к обсуждаемой формуле
|
|
|
(6.28) |
Эта скорость называется групповой скоростью. Поскольку, как мы уже знаем, энергия колебаний определяется их амплитудой, «перемещение» последней и означает, что групповая скорость является скоростью переноса энергии волновым пакетом.
Фазовая же скорость волны есть отношение частоты к волновому числу:
|
|
|
(6.29) |
Дифференцируя это соотношение по k, находим связь фазовой и групповой скоростей:
|
|
|
(6.30) |
Учитывая связь волнового числа с длиной волны
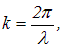
формулу (6.30) можно переписать в виде
|
|
|
(6.31) |
Очевидно, что в отсутствие дисперсии
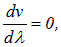
и групповая скорость не отличается от фазовой.
Групповая скорость как скорость распространения энергии в среде не может быть больше скорости света в вакууме, то есть всегда 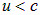 , в то время как фазовая скорость света в среде не является предельной и может оказаться меньше скорости движения частиц в среде, например электронов. В этом случае, как мы уже знаем, возникает излучение Черенкова — Вавилова.
, в то время как фазовая скорость света в среде не является предельной и может оказаться меньше скорости движения частиц в среде, например электронов. В этом случае, как мы уже знаем, возникает излучение Черенкова — Вавилова.
Game: Perform tasks and rest cool.2 people play!
Play gameСветовая волна несет энергию электромагнитного поля. При прохождении света через вещество происходит потеря энергии из-за превращения ее в различные формы внутренней энергии вещества или энергию вторичного излучения, которое может отличаться от первичного спектральным составом и направлением распространения. Поглощение света может приводить к нагреванию вещества или возбуждению атомов и молекул, к фотохимическим процессам и т. д.
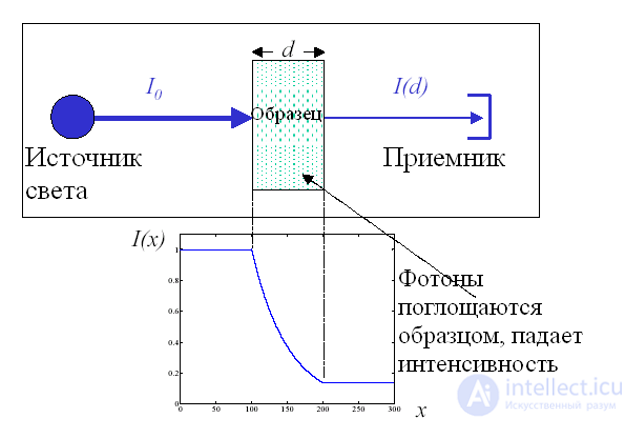
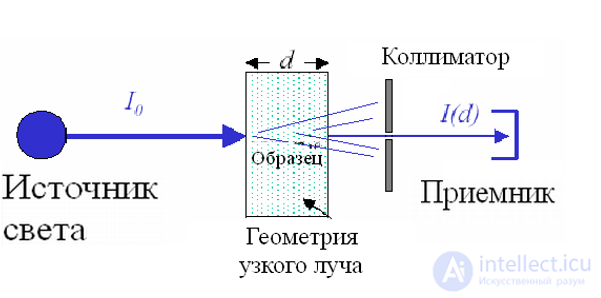
Если световая волна с интенсивностью в данной точке I(х) проходит через слой толщиной dх, то ее интенсивность уменьшается на величину, пропорциональную толщине слоя и интенсивности волны в данном месте:
|
|
|
(6.32) |
где 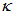 — коэффициент поглощения, зависящий от свойств поглощающего вещества.
— коэффициент поглощения, зависящий от свойств поглощающего вещества.
Преобразуем полученное дифференциальное уравнение:
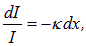
и проинтегрируем
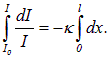
В результате интегрирования получаем
|
|
|
(6.33) |
где I0 — падающий световой поток, I — толщина поглощающего слоя вещества. Это соотношение называется законом Бугера — Ламберта — Бера. Он справедлив для монохроматического света.
Соотношение (6.33) можно записать в виде
|
|
|
(6.34) |
где
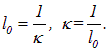
Отсюда вытекает физический смысл k; коэффициент поглощения обратно пропорционален толщине слоя вещества, при прохождении которого интенсивность света уменьшается в е = 2.72 раза.
Резонансное поглощение происходит при частотах, близких к собственным, энергия передается от действующего поля атомам вещества, и амплитуда их колебаний значительно возрастает. Заряженные частицы среды приводятся в колебательное движение электрическим полем действующей волны и повторно испускают свет той же частоты как у первичной волны.
ПОГЛОЩЕНИЕ СВЕТА БИОЛОГИЧЕСКИМИ ТКАНЯМИ
Game: Perform tasks and rest cool.2 people play!
Play game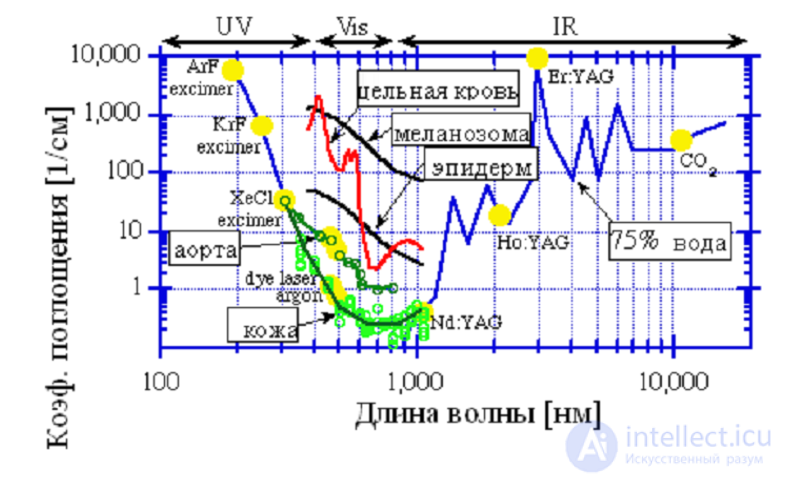
Мы наблюдаем красное Солнце на закате и голубое небо в ясный день. Эти явления можно объяснить рассеянием света на флуктуациях плотности газа составляющего атмосферу — воздуха. поляризует газ, в результате чего каждый его небольшой объем с линейным размером меньше или порядка длины волны приобретает изменяющийся во времени электрический дипольный момент и сам становится источником излучения, частота которого равна частоте - падающего света. «Хитрость» в том, что интенсивность вторичных – излучаемых газом волн пропорциональна четвертой степени их частоты. То есть голубой свет рассеивается на порядок более интенсивно, чем красный. Днем, глядя на небо, мы видим рассеянный голубой свет. Во время восхода или заката Солнца мы видим прошедший через атмосферу свет, обогащенный слабо рассеивающейся длинноволновой красной компонентой. Более подробное рассмотрение следует ниже.
В теории излучения на основе уравнений Максвелла показывается, что мощность вторичного излучения пропорциональна квадрату ускорения заряженной частицы. Если электроны под действием световой волны колеблются по закону
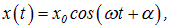
то их ускорение
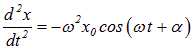
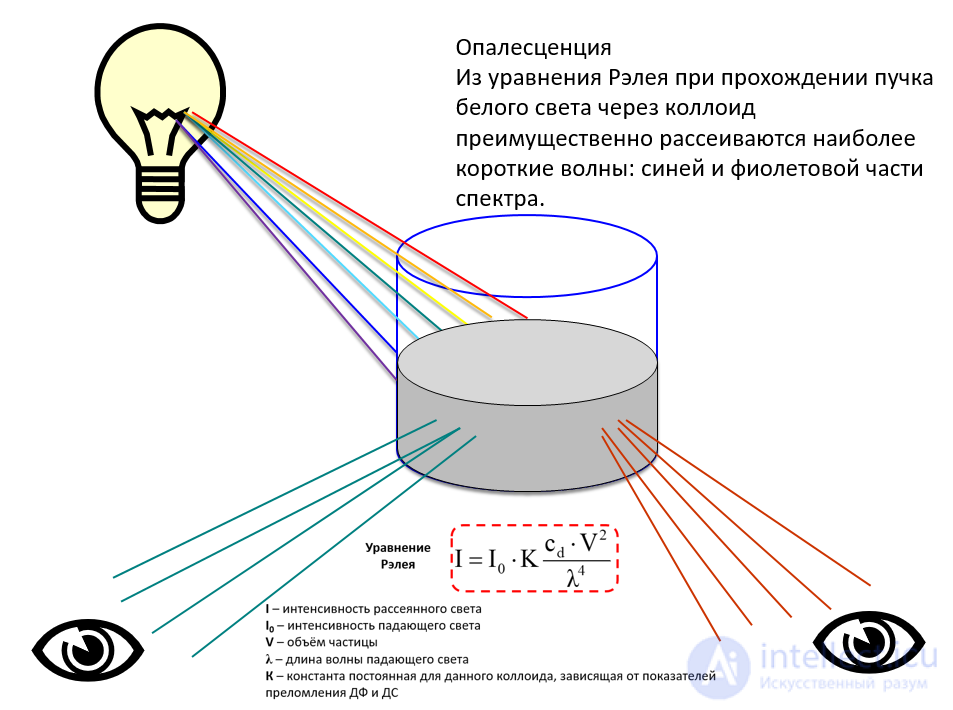
пропорционально квадрату частоты 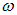 . Соответственно, мощность вторичного излучения пропорциональна четвертой степени частоты. Поэтому и интенсивность рассеянного света пропорциональна частоте в четвертой степени частоты или обратно пропорциональна четвертой степени длины световой волны — закон Рэлея:
. Соответственно, мощность вторичного излучения пропорциональна четвертой степени частоты. Поэтому и интенсивность рассеянного света пропорциональна частоте в четвертой степени частоты или обратно пропорциональна четвертой степени длины световой волны — закон Рэлея:
|
|
|
(6.35) |
Следовательно, красный и оранжевый свет рассеиваются гораздо слабее, чем голубой и фиолетовый, и поэтому небо в ясный день выглядит голубым. На закате солнечные лучи проходят максимальный слой атмосферы. Значительная часть голубого излучения рассеивается и не попадает в глаз наблюдателя. Поэтому прошедший луч, достигающий поверхности Земли, лишается голубой и фиолетовой составляющих и поэтому кажется красноватым.
Следует отметить, что закон Рэлея имеет место только в случае, когда рассеивающие объекты оказываются меньше длины световой волны. Но, к примеру, облака содержат капельки воды и кристаллы льда, размеры которых значительно превышают длину волны. Множество таких частиц рассеивает свет почти равномерно на всех частотах, главным образом за счет отражения света на поверхностях этих частиц, а не собственно рассеяния, если под ним понимать излучение вторичных волн. Поскольку коэффициент отражения практически не зависит от частоты и снег и облака и соль в солонке кажутся белыми.
Помимо рэлеевского рассеяния существуют другие процессы рассеяния, в частности, с изменением частоты рассеянного света, такие, как комбинационное рассеяние света, которое будет рассмотрено позднее.
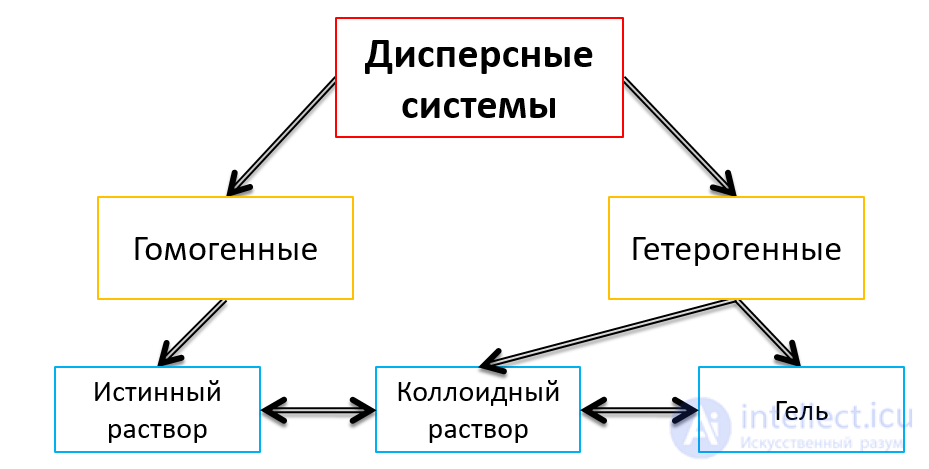
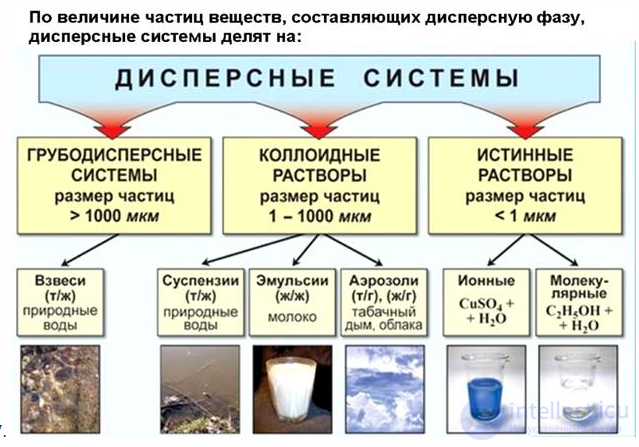
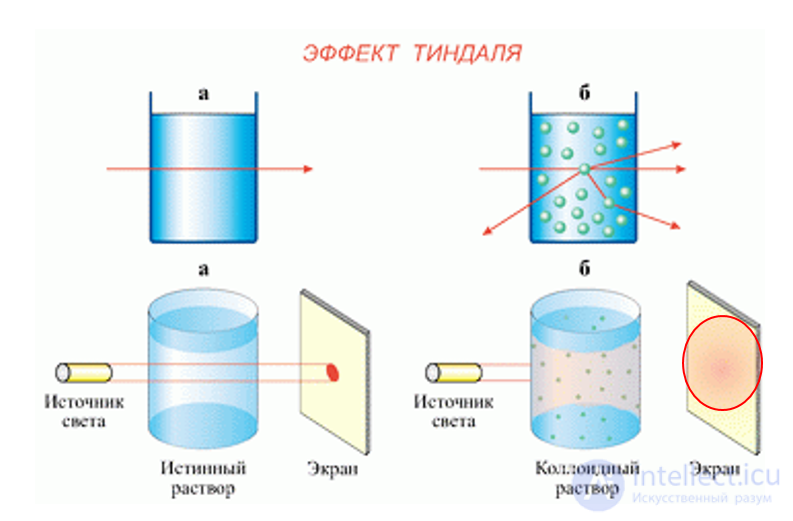
Эффект Тинда́ля, рассеяние Тинда́ля (англ. Tyndall effect) — оптический эффект, рассеивание света при прохождении светового пучка через оптически неоднородную среду. Обычно наблюдается в виде светящегося конуса (конус Тиндаля), видимого на темном фоне.
Характерен для растворов коллоидных систем (например, золей металлов, разбавленных латексов, табачного дыма), в которых частицы и окружающая их среда различаются по показателю преломления. На эффекте Тиндаля основан ряд оптических методов определения размеров, формы и концентрации коллоидных частиц и макромолекул.
Game: Perform tasks and rest cool.2 people play!
Play gameТиндаля эффект воспринимается невооруженным глазом как равномерное свечение некоторой части объема рассеивающей свет системы. Свет исходит от отдельных точек - дифракционных пятен, хорошо различимых под оптическим микроскопом при достаточно сильном освещении разбавленного золя. Интенсивность рассеянного в данном направлении света (при постоянных параметрах падающего света) зависит от числа рассеивающих частиц и их размера.

Солнечные лучи, проходящие сквозь туман

Подобные явления, которые не являются рассеянием Тиндаля
Как определить, имеет ли жидкость свойства золя? Определение происходит на основе эффекта Тиндаля: когда тонкий луч света (например, луч лазерной указки) проходит через коллоидный раствор, то свет рассеивается, и луч приобретает форму конуса. На фотографии рассеивание происходит в растворе яичного белка (дальний стакан), а в растворе поваренной соли в ближнем стакане рассеивание не наблюдается
Когда дневное небо затянуто облаками , солнечный свет проходит через мутный слой облаков, в результате чего на земле появляется рассеянный свет ( солнечный луч ). Это демонстрирует рассеяние Ми вместо рассеяния Тиндаля, потому что облачные капли больше, чем длина волны света, и рассеивают все цвета примерно одинаково. Когда дневное небо безоблачно , цвет неба синий из-за рэлеевского рассеяния, а не тиндаля, потому что рассеивающие частицы - это молекулы воздуха, которые намного меньше длины волны видимого света. [10]Точно так же термин эффект Тиндаля неправильно применяется к рассеянию света большими макроскопическими частицами пыли в воздухе; однако из-за их большого размера они не проявляют тиндалевского рассеяния
Опалесценция [опал + лат. escentia («слабое действие», свечение)] — физическое явление рассеяния света мутной средой, обусловленное ее оптической неоднородностью; наблюдается, например, при освещении большинства коллоидных растворов, а также у веществ в критическом состоянии (критическая опалесценция).
Критическая опалесценция — оптическое явление резкого усиления рассеяния света чистыми жидкостями и газами при достижении критической точки, а также растворами в критических точках смешения. Причиной является резкое возрастание сжимаемости вещества, сопровождаемое усилением флуктуаций плотности (в том числе микрочастиц в растворах), на которых и происходит рассеяние света.

опалесценция черного опала

рэлеевское рассеяние в белом опале

рэлеевское рассеяние
в опалесцирующем стекле:
оно оранжеватое на просвет, и голубоватое при взгляде с других направлений. То же и в разбавленном молоке, белом дыме, и т.п.
Game: Perform tasks and rest cool.2 people play!
Play gameИсследование, описанное в статье про поглощение света, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое поглощение света, рассеяние света, дисперсия света, поляризация света, опалесценция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Колебания и волны (Оптика, акустика и радиофизика)
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика