Примеры решения задач к разделу Линейная алгебра и аналитическая геометрия

Привет, мой друг, тебе интересно узнать все про задачи линейная алгебра, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое задачи линейная алгебра, задачи аналитическая геометрия , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

Пример N 1

В ПДСК даны векторы 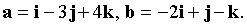Найти единичный вектор x, перпендикулярный векторам a, b .

Решение.

Вектор c = a × b перпендикулярен векторам a, b.

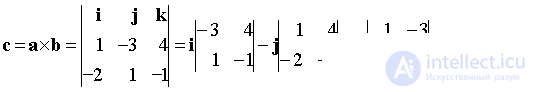
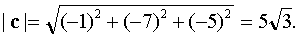
В качестве искомого вектора x можно взять вектор 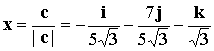или вектор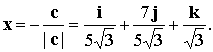

Векторы 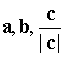образуют правую тройку векторов, а 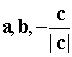- левую.

Ответ: 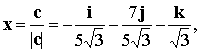или

Пример N 2

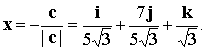
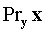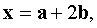
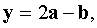
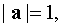
Найти , если известно, что 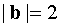, угол φ между векторами a, b равен φ / 6.

Решение.

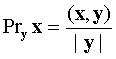. Используя свойства скалярного произведения, находим

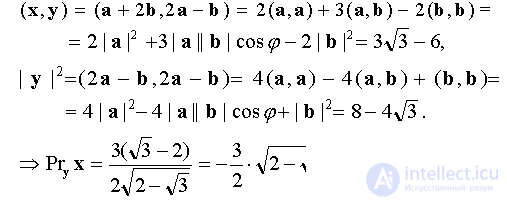
Ответ: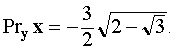

Пример N 3

В ПДСК заданы векторы 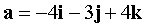, , 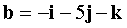, 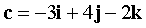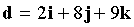. Доказать, что векторы a, b, c образуют базис, и найти разложение вектора d по базису a, b, c .

Решение.

Находим определитель, составленный из координат векторов a, b, c :

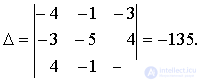
Т.к. Δ ≠ 0, то a, b, c - базис. Теперь найдем разложение вектора d по базису a, b, c . Следует найти числа α₁, α₂, α₃ такие, что aα₁ + bα₂ + cα₃ = d. В развернутом виде это равенство является линейной системой алгебраических уравнений с неизвестными α₁, α₂, α₃ :

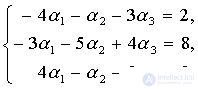
По формулам Крамера находим:

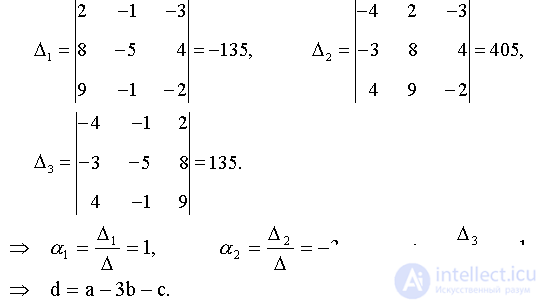
Ответ: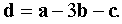

Пример N 4

В ПДСК заданы векторы 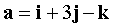, , 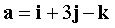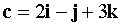. Найти вектор x такой, чтобы его скалярное произведение с векторами a, b, c равнялось - 12, 6, - 8 соответственно.

Решение.

Пусть 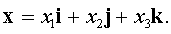Из условия задачи получаем

Необходимо решить систему линейных алгебраических уравнений с неизвестными x₁, x₂, x₃. По формулам Крамера находим

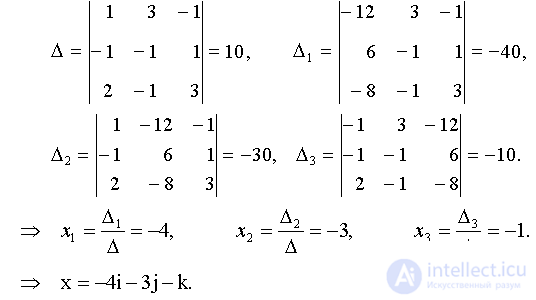
Ответ: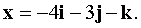

Пример N 5

В ПДСК заданы векторы 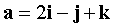, 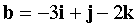. Найти площадь параллелограмма, построенного на векторах x, y где вектор x перпендикулярен векторам a, b, и x = 3, а вектор
y = a + b.

Решение.

Вектор c = a × b перпендикулярен векторам a, b

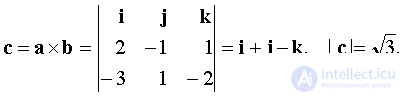
Вектор x должен быть коллинеарен вектору c. Так как по условию задачи x = 3, то 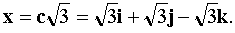Находим ,

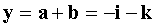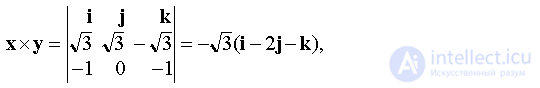
площадь параллелограмма, построенного на векторах x, y .

Ответ: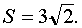

Пример N 6

В ПДСК заданы векторы 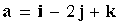, 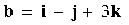и точки 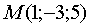, 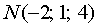. Найти объем параллелепипеда, построенного на векторах 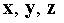где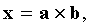

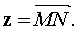
Решение.

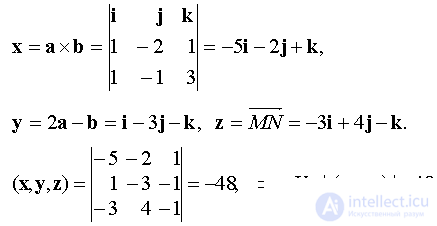- объем параллелепипеда, построенного на векторах .

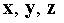Ответ: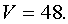

Пример N 7

При каком значении x будут компланарны векторы a, b, c если

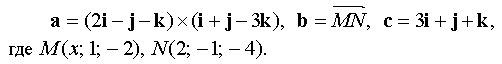
Решение.

Векторы a, b, c будут компланарны, если (a, b, c) = 0.

Ответ: x = 8.

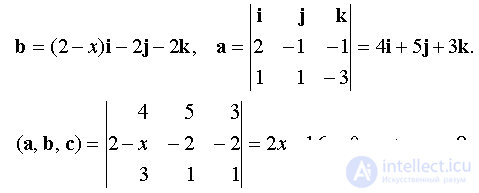
Пример N 8

В треугольнике с вершинами K(-5; 4), L(1; -4), M(-9; 1) найти:
а) уравнение прямой, содержащей опущенную из вершины L высоту;
б) длину высоты, опущенной из вершины L ;
в) точку N , симметричную точке L , относительно прямой, проходящей через точки K, M ;
г) уравнение прямой, содержащей биссектрису угла L .

Решение.

а) вектор нормали прямой (Lh) , содержащей высоту, является вектор 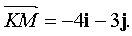Находим уравнение прямой

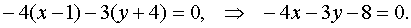
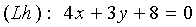- уравнение прямой, содержащей опущенную из вершины высоту;

б) длина высоты, опущенной из вершины L равна расстоянию ρ от точки L до прямой (K,M) , проходящей через точки K, M.

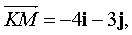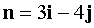Найдем уравнение этой прямой. Т.к. то - вектор нормали этой прямой. Находим общее уравнение прямой (K,M) :

Нормальное уравнение прямой (K,M) имеет вид

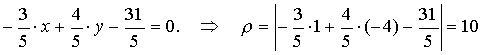- длина высоты;

в) чтобы найти точку N необходимо определить точку пересечения 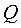прямых (Lh), (KM) т.е. необходимо решить систему линейных уравнений

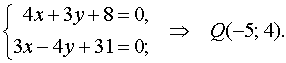
Теперь находим точку N (x; y) : .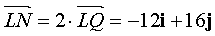

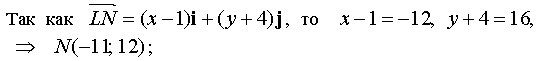
г) вектор 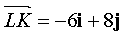является вектором прямой (LK), а вектор 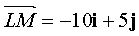- прямой (LM). Пусть 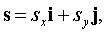где s_x, s_y - неизвестные вектор прямой ( Ll ), содержащей биссектрису угла L. Вектор s образует с векторами 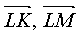равные углы. Следовательно, 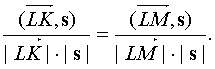Так как

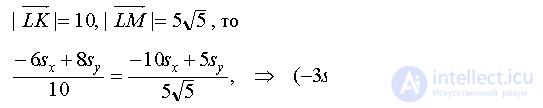
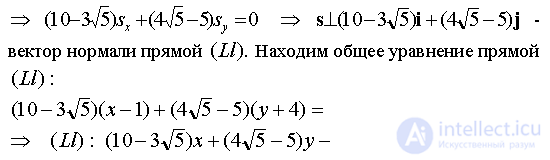
Ответ:

Задачи с линиями 2-го порядка.

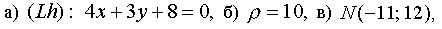
Данный практикум представляет собой логическое продолжение лекции о линиях второго порядка и ее популярных представителях – эллипсе, гиперболе и параболе. Сегодня мы закрепим пройденный материал многочисленными задачами, и, кроме того, дополним теоретический багаж знаниями, которые я намеренно скрыл на первых занятиях, чтобы не перегружать «чайников» новой информацией. Признаюсь честно, ненавижу вымучивать первые абзацы своих статей (особенно, когда готов четкий план урока), поэтому разольем кофе по чашкам, сядем в круг и перейдем к обсуждению вопросов по существу.

В самостоятельных и контрольных работах наиболее часто встречаются следующие задания:

– Найти геометрическое место точек (или составить уравнение множества точек), каждая из которых удовлетворяет определенным аналитическим условиям. Безусловно, данная формулировка является общей и не факт, что в итоге должна получиться обязательно линия, и обязательно второго порядка. Однако в контексте рассматриваемой темы эти магические слова практически всегда вызывают к жизни уравнение эллипса, окружности, гиперболы либо параболы.

– Постройте кривую заданную уравнением - Привести уравнение линии 2-го порядка к каноническому виду. Понятие канонического вида уравнения, а также некоторые элементы этой задачи многим читателям уже знакомы, и в ближайшем будущем вам представится отличная возможность продвинуться дальше.

Нередко оба блюда подаются за один раз, то есть сначала требуется составить уравнение линии, а затем привести его к каноническому виду + в качестве десерта найти вершины, фокусы, эксцентриситет, директрисы, выполнить чертеж и т.д. Как гостеприимный хозяин заведения постараюсь всех накормить досыта, да так – чтобы некоторые не только с трудом вышли из-за стола, но и остались здесь на ночевку =) Начислим для аппетита:

Задача 1

Составить уравнение линии, расстояние каждой точки которой от точки 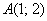в два раза больше, чем от точки 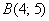. Выполнить чертеж. Привести полученное уравнение к каноническому виду.

Решение данной задачи всегда начинается стандартно – в рассмотрение вводится некоторая точка 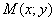с переменными координатами, которая принадлежит искомой линии.

Таким образом, наша аналитическая формулировка конкретизируется следующим образом: «составить уравнение линии, расстояние каждой точки 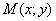которой от точки 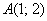в два раза больше, чем от точки 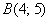». Немного приостановимся и ответим на ключевой вопрос: о чем здесь идет речь? Очевидно, что задач можно придумать бесконечно много, поэтому, в первую очередь необходимо правильно понять условие.

А речь здесь идет о расстоянии 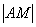от точки «а» до точки «эм» и о расстоянии 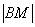от точки «бэ» до той же точки «эм». Формула длины отрезка нам хорошо знакома еще с первого урока по аналитической геометрии. Напоминаю: расстояние между двумя точками 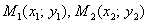рассчитывается по формуле .

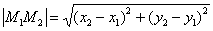Запишем длины соответствующих отрезков:

для точек 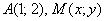расстояние ;
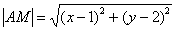для точек 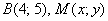расстояние .

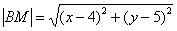Теперь нужно составить уравнение. Согласно условию, расстояние в два раза больше расстояния 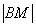, следовательно, справедливо равенство:

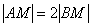
Или:

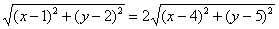
Уравнение успешно составлено, но какую линию оно задает – совершенно не понятно. Поэтому дальнейшие действия состоят в упрощении полученной конструкции, и сейчас мы ознакомимся с типовым техническим алгоритмом.

Во-первых, избавимся от корней. Для этого возведем в квадрат обе части:

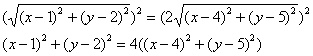
активно пользуясь формулами сокращенного умножения, раскроем все скобки:

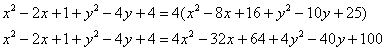
перенесем все в левую часть и приведем подобные слагаемые:

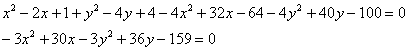
разделим каждое слагаемое на –3:

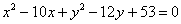
Получено уравнение линии 2-го порядка в общем виде. Уже лучше, однако, и оно как неведома зверушка. По этой причине вторая часть преобразований состоит в попытке приведения уравнения к каноническому виду. Перед нами не самый тяжелый случай, который уже фигурировал в конце статьи о линиях второго порядка. Искусственным приемом выделяем полные квадраты:

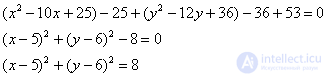
и завершающим штрихом рождаем квадрат в правой части:
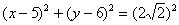– уравнение окружности с центром в точке 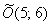радиуса 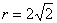. Возьмем в руки остроногого друга:

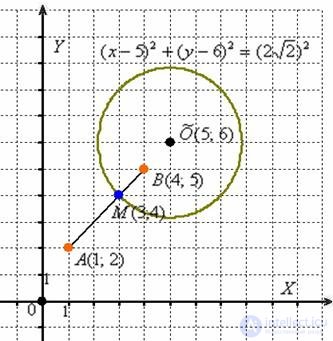
Не лишней будет кустарная, но эффективная геометрическая проверка. По условию для любой точки 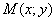построенной линии расстояние 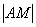должно быть в 2 раза больше расстояния 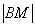. Мысленно выбираем наиболее удобную точку 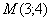нашей окружности и убеждаемся в справедливости данного соотношения. В целях контроля можно взять еще какую-нибудь точку и измерить длины отрезков 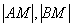обычной линейкой.

Заключительная часть задания состоит в приведении уравнения линии к каноническому виду. Центр канонической окружности должен располагаться в начале координат, и, как я неоднократно оговаривался, есть два способа разрулить ситуацию.

Первый, более простой метод:

1) Приведем уравнение окружности к каноническому виду путем ее параллельного переноса центром в начало координат: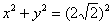

Второй, более солидный и правильный метод:

2) Осуществим параллельный перенос прямоугольной системы координат началом в точку :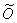

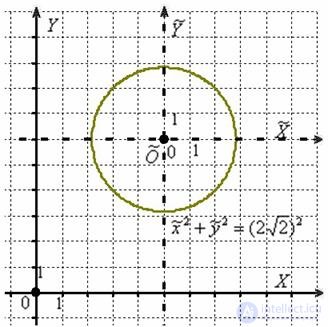
Иными словами, мы перешли к новой системе координат 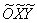ТАК, чтобы уравнение нашей окружности записалось в ней каноническим образом: .

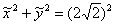На первый взгляд кажется нелепым менять систему координат из-за одной-единственной линии, но на самом деле этот подход более корректен, и об одной простой причине его корректности я расскажу на уроке Приведение уравнения линии 2-го порядка к каноническому виду.

Ответ: искомая линия 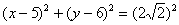представляет собой окружность с центром в точке 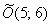радиуса 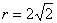. Каноническое уравнение: 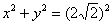(либо 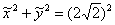в зависимости от способа приведения).

Аналогичный пример для самостоятельного решения:

Задача 2

Составить уравнение множества точек, для каждой из которых сумма квадратов расстояний от точек 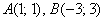равна 20. Определить тип линии, выполнить чертеж и привести уравнение к каноническому виду. Указать координаты фокусов, записать уравнение асимптот, если они есть. Вычислить эксцентриситет кривой.

Решение: Пусть точка 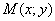принадлежит искомому множеству точек. Тогда:


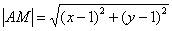
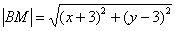
По условию:

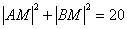
Или:

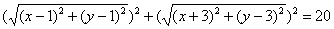
Упростим уравнение:

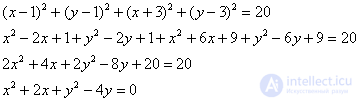
Выделим полные квадраты:

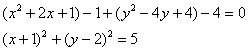
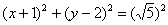– окружность с центром в точке 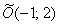радиуса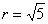
Выполним чертеж:

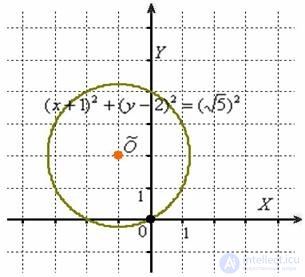
Приведем уравнение к каноническому виду.
1) Способ первый. Осуществим параллельный перенос окружности центром в начало координат: .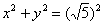
2) Способ второй. С помощью параллельного переноса перейдем от исходной к новой прямоугольной системе координат 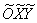с началом в точке 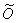. Таким образом, уравнение окружности запишется в каноническом виде: .
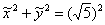Ответ: уравнение искомого множества точек 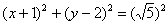задает окружность с центром в точке 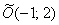радиуса 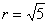. Канонический вид уравнения: 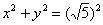(или 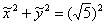в зависимости от способа). Фокусы окружности совпадают и находятся в ее центре. У окружности отсутствуют асимптоты. Эксцентриситет любой окружности равен нулю.

Систематизируем порядок решения данной задачи:

На первом шаге необходимо рассмотреть точку 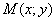с неизвестными координатами, которая принадлежит искомому множеству точек, и разобраться в условии задачи. Об этом говорит сайт https://intellect.icu . Как правило, в нем говорится о расстояниях от точки «эм» до других точек и/или других линий, а также о соотношениях этих длин.

На втором шаге следует найти длины нужных отрезков и в соответствии с аналитическим условием задачи составить уравнение.

На третьем шаге осуществляем упрощение полученного уравнения. Сначала приводим его к общему виду, а затем к форме, которая близкА к канонической. В некоторых задачах сразу получается каноническое уравнение.

На четвертом шаге – чертеж.

На пятом – приведение к каноническому виду.

На шестом – фокусы, асимптоты, эксцентриситет. Напоминаю, что находить их гораздо удобнее именно из канонической записи.

На практике чаще всего заданий меньше, так, в некоторых случаях не надо приводить уравнение к каноническому виду, а в самой компактной версии не требуется и чертежа – достаточно лишь упростить уравнение и назвать линию. Я специально «нагружаю» условия задач, чтобы образцы решений годились «на все случаи жизни». Но, тем не менее, надрываться тоже не будем, и разогреемся парой новых коктейлей:

Задача 3

Составить уравнение множества точек, для каждой из которых квадрат расстояния до точки 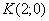на 16 больше квадрата расстояния до оси ординат.

Решение: Пусть точка 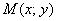принадлежит искомому множеству. Тогда:

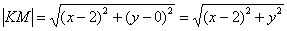
Примечание: строго говоря, в соответствии с формулировкой условия нужно рассмотреть 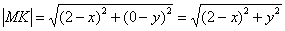(та же самая длина), но в этой и других задачах мы пренебрежем данной логической неточностью.

Чему равно расстояние от точки 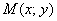до оси ординат? Можно воспользоваться стандартной формулой расстояния от точки до прямой, но если немного подключить воображение, то легко понять, что расстояние от любой точки до оси 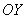равно модулю ее «иксовой» координаты:

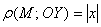
По условию 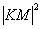на 16 больше, чем 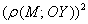, следовательно, справедливо следующее равенство:

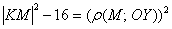
(либо )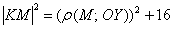

Таким образом:

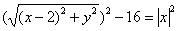
Раскручиваем гайки:

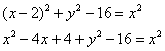
«Иксы в квадрате» взаимоуничтожаются, и, очевидно, уравнение нужно максимально приблизить к каноническому виду :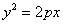

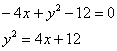
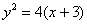– парабола с вершиной в точке 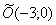, фокальным параметром .

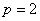Ответ: искомое множество точек представляет собой параболу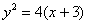

Если дополнительно требуется привести уравнение линии к каноническому виду, то в данном примере это осуществляется элементарно:

1) Приведем уравнение параболы к каноническому виду путем ее параллельного переноса центром в начало координат: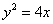

2) Перейдем к новой прямоугольной системе координат 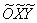с центром в точке 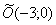, тогда уравнение параболы примет вид: .

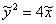Чертеж приводить не буду, поскольку параболу 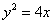мы уже вертели, как хотели.

Задача 4

Составить уравнение множества точек, для каждой из которых расстояние до точки 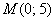равно расстоянию до оси абсцисс. Выполнить чертеж. Привести уравнение к каноническому виду.

В образце решения последний пункт реализован обоими способами.

Разобранные задачи с окружностями (особенно часто), параболами встречаются и в школьной программе.

Решение: пусть точка 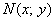принадлежит искомому множеству точек. Тогда:

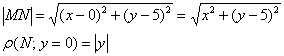
По условию:

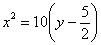– парабола, ветви которой направлены вверх, с вершиной 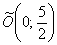и фокальным параметром :

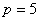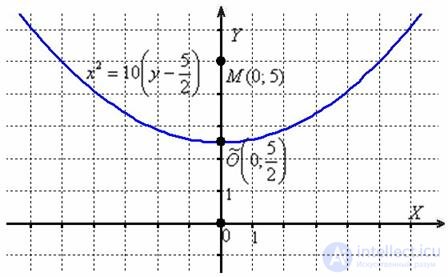
Примечание: аналитическое условие задачи формулирует определение данной параболы, т.е. точка 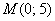является ее фокусом, а ось абсцисс – директрисой.
Приведем уравнение кривой к каноническому виду:
1) Осуществим параллельный перенос параболы 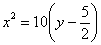вершиной в начало координат: 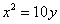и повернем ее на 90 градусов по часовой стрелке: .
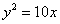Либо так: повернем параболу 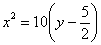по часовой стрелке на 90 градусов относительно точки 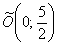: 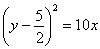и перенесем ее в начало координат: .

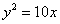2) Повернем прямоугольную систему координат 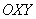на 90 градусов против часовой стрелки и перенесем ее началом координат в точку 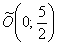. Тогда в новой системе координат 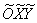уравнение данной параболы примет канонический вид .
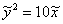Ответ: 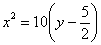– парабола. Каноническое уравнение: 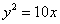(либо 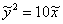в зависимости от способа приведения).

Задача 5

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки 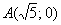к расстоянию до прямой 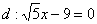постоянно и равно 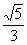. Сделать чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы (если они существуют).

Решение: пусть точка 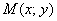принадлежит искомому множеству точек. В задаче говорится о расстоянии:
,

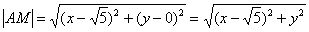а также о расстоянии от точки до прямой, которое вычисляется по формул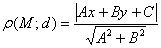е , где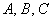 – соответствующие коэффициенты общего уравнения прямой «дэ», 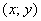– координаты точки «эм».

В данном случае:
.

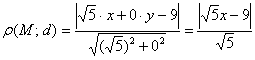По условию для каждой точки 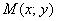отношение расстояния 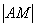к расстоянию 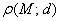должно быть равно 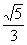. А что такое отношение? Отношение – это пропорция, или попросту дробь:

Уравнение составлено, но его вид оставляет желать лучшего. Сначала избавимся от трехэтажной дроби. Для этого знаменатель левой части (дробь) перекинем направо:

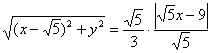
Сократим на :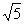

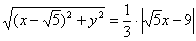
Чтобы окончательно избавиться от дробей, «поднимем тройку» на левый берег:

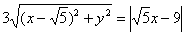
Дальнейшие упрощения приобретают знакомые очертания. Возводим обе части в квадрат и раскрываем скобки:

Перенесем все налево и причешем слагаемые:

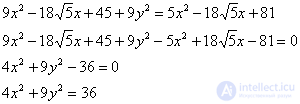
Читатели с хорошим и высоким уровнем подготовки, разумеется, могут немного видоизменять вычисления и сокращать запись, выполняя некоторые действия в уме.

Разделим обе части на 36:

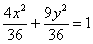
Организуем трехэтажные дроби:

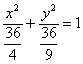
И выполним деление:

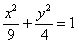
Почему целесообразен именно такой алгоритм, подробно закомментировано в Примере 4 статьи о гиперболе и параболе.

В результате:
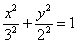– эллипс с центром в начале координат, полуосями .

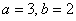Обратите внимание, что такая формулировка однозначно определяет эллипс и добавлять что-либо излишне.

Изобразим на чертеже найденный эллипс, точку 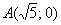и прямую :

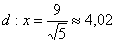Геометрическая проверка тут затруднена, но с другой стороны и не сверхъестественна. Возьмем какую-нибудь точку эллипса, проще всего рассмотреть .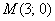
Для нее: .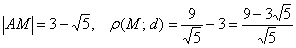
По условию отношение 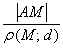должно равняться .
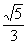Проверяем: 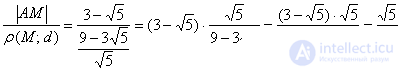, что и требовалось проверить.

На практике можно выбрать любую точку эллипса, измерить расстояния линейкой, разделить 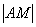на 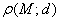с помощью калькулятора и удостовериться, что получилось примерно .

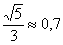В данной задаче уравнение линии нарисовалось сразу в каноническом виде, что облегчает решение. Осталось разобраться с фокусами, эксцентриситетом, асимптотами и директрисами.

Очевидно, что у эллипса отсутствуют асимптоты.

Вычислим 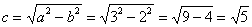и запишем фокусы эллипса:

.

Первый фокус совпал с точкой .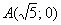

Найдем эксцентриситет: 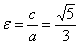. По еще одному странному совпадению эксцентриситет оказался равен отношению .

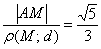…однако, совпадения ли это?

Директрисы эллипса

Директриса, как вы помните из материалов о параболе, – это прямая. Причем прямая с армией горячих поклонников :D ...ну что же, шалуны, завидуйте, у эллипса их две!

Эллипс имеет две директрисы, и в каноническом положении 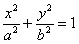они задаются уравнениями , где «эпсилон» – эксцентриситет данного эллипса.

Для нашего героя :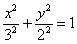

Так и есть, первая директриса полностью совпала с прямой «дэ». Более того, в условии задачи фактически сформулирована следующая теорема аналитической геометрии:

Эллипс – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от нее до соответствующей (ближайшей) директрисы равно эксцентриситету:

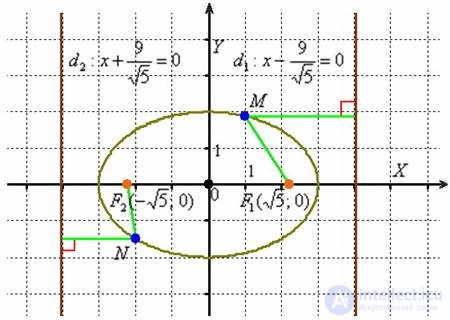
То есть, для любой точки 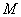эллипса отношение ее расстояния от фокуса 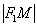к расстоянию от нее же до ближайшей директрисы 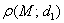в точности равно эксцентриситету: .

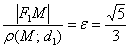Со вторым фокусом и второй директрисой аналогичная история, какую бы точку 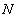эллипса мы ни взяли – будет справедливо отношение: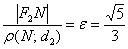

Ответ: искомое геометрическое место точек представляет собой эллипс с фокусами 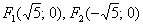и эксцентриситетом 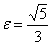. Уравнения директрис: .

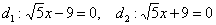Похожий пример для самостоятельного решения:

Задача 6

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки 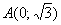к расстоянию до прямой 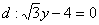постоянно и равно 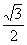. Выполнить чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы, если они существуют.

В образце решения концовка реализована обоими способами, выбирайте версию, которая более уместна в вашем курсе высшей математики.

Решение: пусть точка 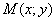принадлежит искомому множеству точек. Тогда:

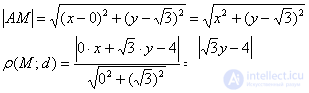
По условию:

Приведем уравнение к каноническому виду:

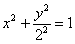– эллипс с центром в начале координат и полуосями, равными 1 и 2.
Примечание: здесь нежелательна формулировка «с полуосями 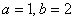», поскольку буквой «а» стандартно обозначают большую полуось, а «единица» таковой не является по причине неканонического положения эллипса.
Выполним чертеж:

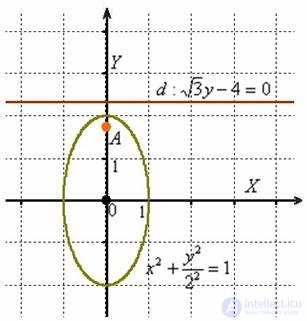
Приведем уравнение к каноническому виду:
1) Способ первый. Повернем эллипс вокруг центра на 90 градусов: .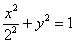
Вычислим 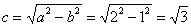и запишем фокусы:
.
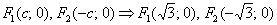Найдем эксцентриситет: .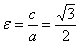
Директрисы эллипса задаются уравнениями 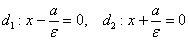, в данном случае:

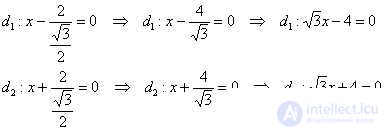
Ответ: искомое множество точек представляет собой эллипс 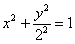. Канонический вид уравнения: 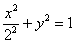. Фокусы: 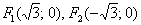, эксцентриситет: 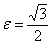, директрисы: .

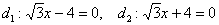2) Способ второй. Используем поворот координатных осей на 90 градусов против часовой стрелки, то есть, перейдем к новой системе координат 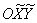(ось 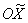совпадет с осью 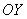старой системы координат, а ось 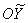будет противоположно направлена к оси 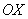). Тогда: .
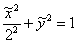! Все дальнейшие действия проводятся в новой системе координат – с переменными !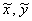
Вычислим 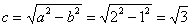и запишем фокусы эллипса:
.
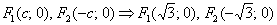Эксцентриситет: .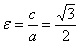
Директрисы эллипса задаются уравнениями 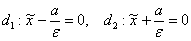, в данном случае:

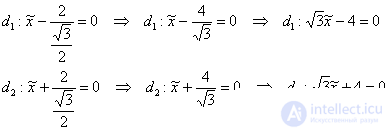
Ответ: искомое множество точек представляет собой эллипс 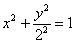. Канонический вид уравнения: 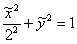. Фокусы: 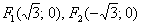, эксцентриситет: 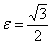, директрисы: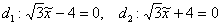

Задача 7

Составить уравнение линии, для каждой из которых разность расстояний до точек 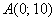и 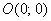по модулю равна 8. Привести уравнение к каноническому виду и выполнить чертеж. Найти асимптоты, фокусы, эксцентриситет и директрисы, если они существуют.

Решение: пусть точка 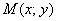принадлежит искомой линии. Тогда:

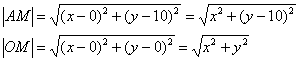
По условию:

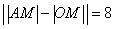
Или:

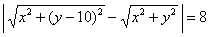
Кстати, ничего не напоминает? Внимательные читатели уже определили линию ;-)

Корни? Модуль? Застрелитесь! Ерунда!

От модуля избавляемся немедленно:

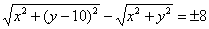
Теперь нужно избавиться от радикалов. Возводить в квадрат сразу – идея плохая (можете попробовать), поэтому разведем корни по углам ринга:

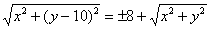
Ну вот, теперь совсем другое дело:

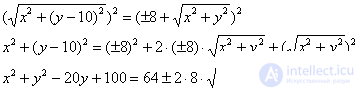
Успехи есть, но один корень остался. Оставим нашего зловреда в одиночестве и максимально упростим левую часть уравнения:

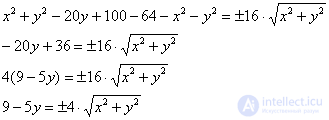
Возводим в квадрат обе части еще раз, и заметьте, как попутно и совершенно спокойно исчезает знак «+–»:

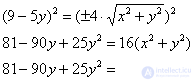
Перебросим все направо и «развернем» уравнение:

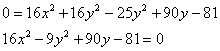
Получено уравнение линии 2-го порядка в общем виде. Выделяем полный квадрат при переменной «игрек», для этого вынесем «минус девять» за скобку:

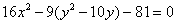
Далее внутри скобки искусственно добавляем +25 (в целях применения формулы на следующем шаге) и, чтобы уравнение не изменилось, за скобками нужно прибавить :

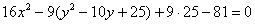
Хорошо осмыслите выполненное действие – фишка распространенная.

Собираем квадрат разности и допиливаем константы:

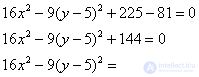
Вот тебе и раз. По всем признакам мыльная опера должна была закончиться гиперболой 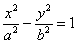, но у нас «лишний» минус. Выполним проверку и раскроем скобки (что желательно сделать в любом случае)… нет, все верно – получается исходное общее уравнение .

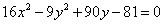Изменим знаки у обеих частей:

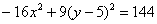
Уже ближе к правде, но «минус» оказался «не на своем месте». В главе о повороте и параллельном переносе гиперболы я рассказывал, что это признак поворота данной кривой на 90 градусов относительно своего канонического положения.

Но давайте сначала доведем до ума уравнение. Делим обе части на 144:

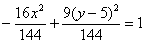
И завершающий тонкий тюнинг:

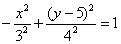– вот она, долгожданная гипербола, удовлетворяющая условию задачи, ...которое фактически представляет собой определение гиперболы =)

По условию требуется сначала привести уравнение к каноническому виду, и только потом выполнить чертеж. Дабы не превысить точку кипения серого вещества, применим упрощенную схему. Однако случай все равно не самый простой. Центр симметрии нашей подопечной находится в точке 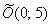, и, кроме того, она повернута на 90 градусов вокруг этой точки

На первом шаге осуществим параллельный перенос гиперболы 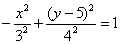ТАК – чтобы ее центр оказался в начале координат. В результате получится уравнение: .

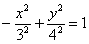Вторым действием повернем гиперболу вокруг начала координат на 90 градусов, при этом меняем местами значения полуосей и перебрасываем «минус» к переменной «игрек»:

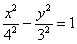
В принципе, операции перестановочны, т.е. сначала можно было повернуть вокруг точки 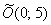, а потом перенести центр в начало координат. Но тут промежуточное уравнение (после поворота) будет другим: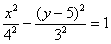

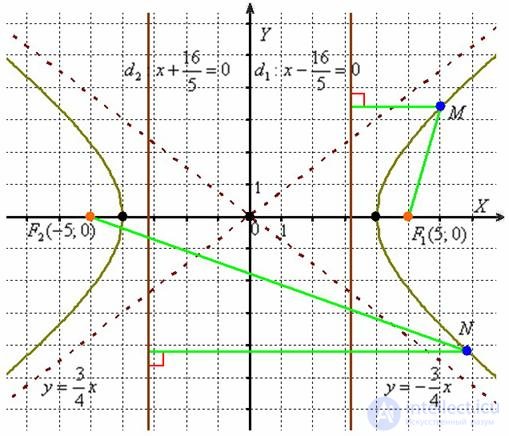
Не забывая про асимптоты , выполним чертеж:

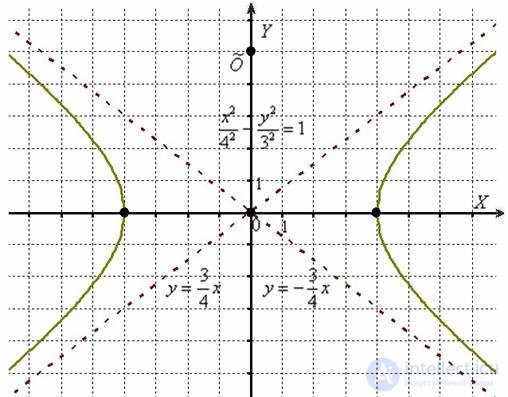
Еще раз: где изначально расположена гипербола? В точке 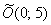(центр симметрии), ветви направлены вверх и вниз. И если по условию вам требуется построить график 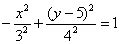, то руководствуйтесь алгоритмом, разобранным в начале урока Гипербола и парабола.

Но работать гораздо удобнее с приведенным уравнением. Найдем фокусы:

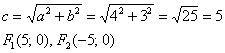
В случае перечисленных выше преобразований они как раз и «переезжают» в точки 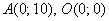условия задачи.

Вычислим эксцентриситет: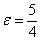

Директрисы гиперболы

У гиперболы, точно так же, как у эллипса, две директрисы. В каноническом случае 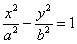они расположены между ветвями гиперболы и задаются такими же уравнениями 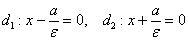, где «эпсилон» эксцентриситет данной гиперболы.

В рассматриваемом примере:

Более того, для гиперболы справедлива абсолютно такая же теорема:

Гипербола – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от нее до соответствующей (ближайшей) директрисы равно эксцентриситету:

То есть, для любой точки 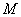гиперболы отношение ее расстояния от фокуса 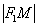к расстоянию от нее же до ближайшей директрисы 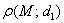равно эксцентриситету: .

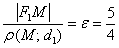Для пары 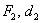и любой точки 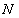гиперболы (ради разнообразия я выбрал демонстрационную точку дальней ветви) отношение такое же: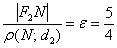

К слову, у параболы с ее единственным фокусом и единственной директрисой по определению эти длины относятся «один к одному», поэтому эксцентриситет любой параболы и равен единице.

Ответ: искомая линия представляет собой гиперболу 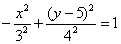с центром симметрии в точке 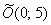и повернутую на 90 градусов относительно своего канонического положения. Канонический вид уравнения: 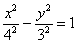, фокусы: 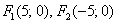, эксцентриситет: 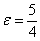, асимптоты: 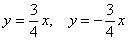, директрисы: .

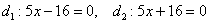Очень хотелось упростить пример, но он взят из конкретной работы, поэтому пришлось с упорным занудством разобрать все-все-все тонкости и технические приемы. Налью всем по стакану молока за вредность и подкину задание для самостоятельного решения:

Задача 8

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки 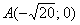к расстоянию до прямой 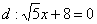постоянно и равно 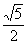. Сделать точный чертеж.

Решение: Пусть точка 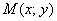принадлежит искомому множеству точек. Тогда:
,
.
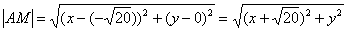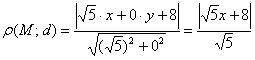По условию:

Упростим уравнение:

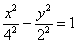– каноническое уравнение гиперболы с действительной полуосью 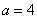, мнимой полуосью .
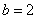Выполним чертеж:

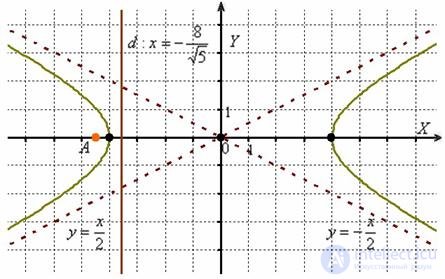
Ответ: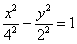
Примечание: точка является вторым фокусом гиперболы, прямая 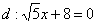– второй директрисой, а их отношение 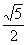– эксцентриситетом.

Как построить линию в полярной системе координат?

Алгоритм построения линии в полярной системе координат

• – Сначала необходимо отметить полюс, изобразить полярную ось и указать масштаб. Кроме того, на первоначальном этапе желательно найти область определения функции, чтобы сразу же исключить из рассмотрения лишние угловые значения.
• – В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.
• – прочертить угловые направления и отметить найденные точки. Как это сделать с помощью каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил в начале статьи о полярных координатах.
• – отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).

Отработаем алгоритм построения на более основательных типовых задачах:

Пример 6

Построить по точкам линию, заданную в полярной системе координат уравнением 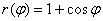, рассматривая значения угла с интервалом в 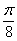рад. Найти уравнение линии в прямоугольной системе координат.

Решение: найдем область определения. Поскольку полярный радиус неотрицателен, то:

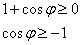
Очевидно, что условие выполнено для любого значения «фи», но, тем не менее, расскажу об удобном графическом способе решения тригонометрического неравенства: изобразите на черновике (или представьте мысленно) график функции 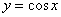левой части неравеснтва и прямую правой части неравенства. Непосредственно по чертежу видно, что синусоида расположена не ниже прямой 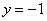, а значит, неравенство 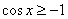выполнено для любого значения «икс».

Итак, на угол 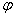не наложено никаких ограничений, и нам предстоит «перепахать» весь круг от 0 до 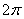, причем, по условию сделать это требуется строго с интервалом в 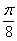рад. (22,5 градусов). Ложку в зубы, калькулятор в руки:

и так далее, пока не будет пройден весь оборот до «двух пи».

На практике обычно не расписывают подробные вычисления, а сразу заносят результаты в таблицу:

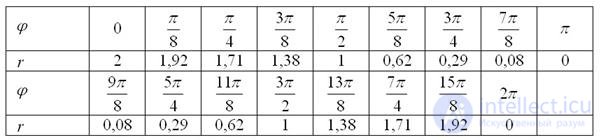
Рекомендую использовать мой расчетный макет, созданный в MS Excel, который позволит буквально в пару щелчков вычислить все значения «эр», сэкономив целый вагон времени. Программу можно раздобыть на странице Математические формулы и таблицы. Особо нетерпеливым читателям предлагаю также воспользоваться handmade-продуктом и быстро начертить заготовку, ориентируясь по клеточкам:

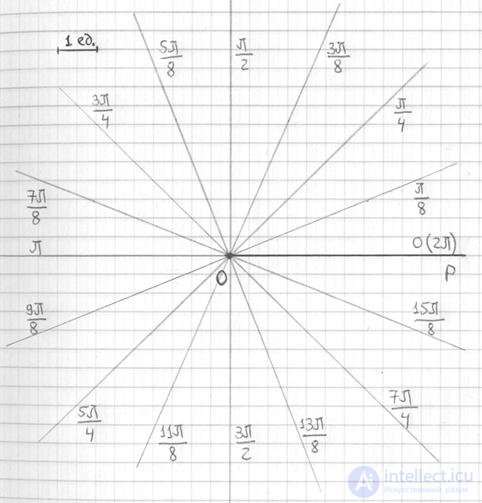
Углы проставлены для удобства и на чистовике, понятно, их записывать не надо.

…поймал себя на мысли, что уже добрые пару лет не выполнял чертежи от руки. Сейчас аккуратно извлеку тетрадь из сканера и спрячу ее в укромном месте – лет через 20-30 продам на антикварном аукционе за 100500 золотых червонцев =) Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта. КИЛОбайта. При этом программисты умудрялись затолкать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). Сейчас на дворе февраль 2014 года, а ведь с той поры не прошло и пары десятилетий. Боюсь, что шутливое сравнение чертежных инструментов с каменным топором довольно скоро перестанет быть шуткой =)

После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:

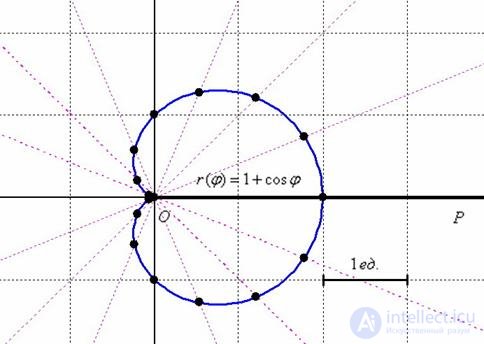
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем, а слишком малые значения для углов 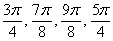допустимо отметить и «на глазок».

Найдем уравнение линии в декартовой системе координат. Для этого используем тоже уже знакомый прием – домножим обе части уравнения 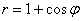на «эр»:

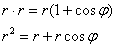
И по формулам перехода к прямоугольным координатам 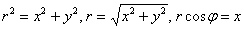получим:

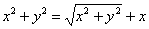
Перенесем «икс» налево и возведем обе части в квадрат:


Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.

Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, обратите внимание, насколько сложной получилась ее формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших порядков посвящены серьезные исследования, и грибники без труда могут отыскать море информации по данной теме. Ну а я, как обычно, предлагаю вкусную и здоровую пищу на каждый день:

Пример 7

Линия задана уравнением 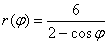в полярной системе координат. Требуется:

1) построить линию по точкам, придавая 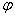значения через интервал 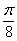, начиная с 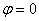и заканчивая ;

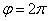2) найти уравнение линии в декартовой системе координат;

3) определить вид кривой.

Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения, а нередко и чертыханья студента. Но только не того, кто прочитал эту и предыдущую статью о полярных координатах! Примерный образец оформления задачи в конце урока.

Рассмотрим еще ряд важных особенностей решения:

Пример 8

Линия задана уравнением 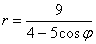в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от 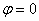до 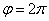и придавая 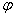значения через промежуток ;

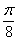2) найти уравнение данной линии в прямоугольной системе координат;

3) назвать линию, найти координаты фокусов и эксцентриситет.

Решение: найдем область определения:

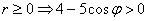
Заметьте, что ноль в знаменателе нас тоже не устраивает, поэтому неравенство становится строгим. Перенесем косинус направо и развернем избушку к лесу задом:

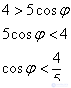
Неравенство несложно решить аналитически, но для лучшего понимания я опять воспользуюсь графическим методом. Изобразим на черновике или представим мысленно графики функций 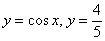, при этом нас будет интересовать только один период – от 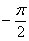до 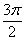. Условию 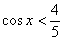удовлетворяет та часть синусоиды, которая расположена ПОД прямой :

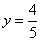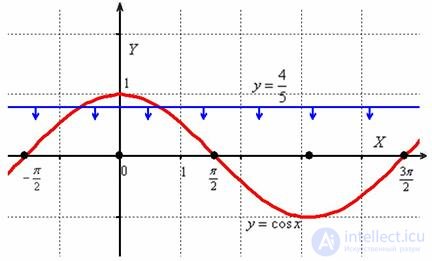
То есть, в нашем распоряжении оказываются почти все значения угла за исключением макушки, расположенной на симметричном отрезке .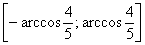

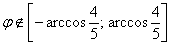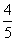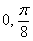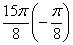Таким образом, . Арккосинус составляет примерно 37 градусов, поэтому из рассмотрения исключаем углы и . Заполним расчетную таблицу с прочерками в соответствующих ячейках:

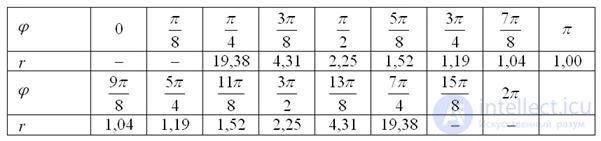
Чайники могут, в принципе, вообще не загружаться областью определения и ставить тире по факту: получилось отрицательное значение «эр» – поставили.

Выполним чертеж:

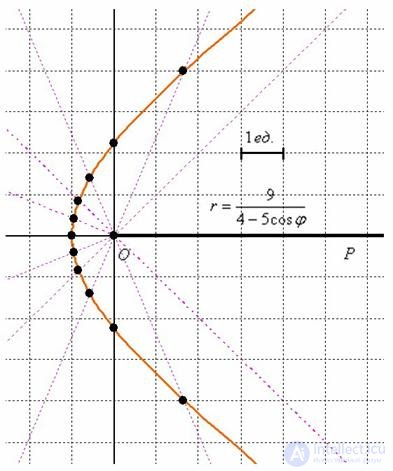
На него не вместились точки, соответствующие значениям 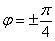, но не уменьшать же из-за этого масштаб. Сойдет и так.

2) Найдем уравнение линии в прямоугольной системе координат. По всем признаком должна получиться гипербола.

Избавляемся от дроби:

Используем формулы перехода :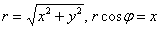

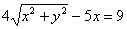
Дальнейшие действия хорошо знакомы из практикума Задачи с линиями 2-го порядка:

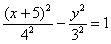– искомое уравнение.

3) Данная линия представляется собой гиперболу с центром в точке 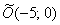, действительной полуосью 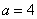, мнимой полуосью 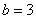. Впрочем, формально по условию можно было и не упоминать о деталях.

Вы спросите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли говорить о целой гиперболе?». Не ошибочно!
И вот по какой причине: если подразумевать обобщенную полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала 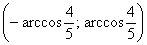прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже противник обобщенных полярных координат, но в данном случае все получается ловко и чертовски удобно – можно как бы и не оговариваться о том, что на чертеже только одна ветвь гиперболы.

Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учетом параллельного переноса гиперболы, к тому же, она не повернута.

Вычислим значение 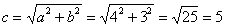и поправкой на параллельный перенос в точку 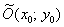найдем фокусы:

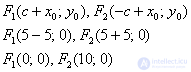
Эксцентриситет: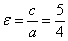

Готово.

Педантичные люди могут еще записать развернутый ответ.

Заключительное задание для самостоятельного решения:

Пример 9

Линия задана уравнением 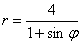в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от 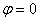до 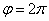и придавая 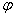значения через промежуток ;

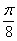2) найти уравнение данной линии в прямоугольной системе координат и определить ее вид.

3) Привести уравнение к каноническому виду и выполнить чертеж в прямоугольной системе координат. Найти фокусы кривой и ее эксцентриситет.

Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз налетал – краем глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к каноническому виду выполнено академическим способом.

На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в навигации (не зря упоминались летчики и самолеты) и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймете, что распиаренная прямоугольная система координат как-то здесь совсем не в тему. Ну а мне пора плотно прикрыть дверь аналитической геометрии и вернуться к матанализу, где полярные координаты тоже эксплуатируются на полную катушку.

До скорых встреч!

Решения и ответы:

Пример 7: Решение: 1) Найдем область определения функции:
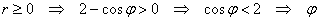– любое.
Заполним таблицу требуемыми значениями угла и соответствующими значениями полярного радиуса:

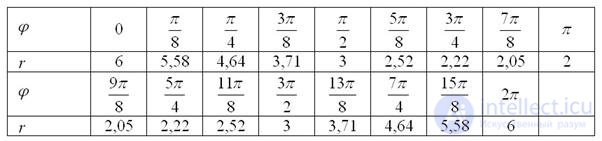
Выполним чертеж:

2) Найдем уравнение линии в декартовой системе координат:

Используем формулы :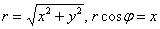

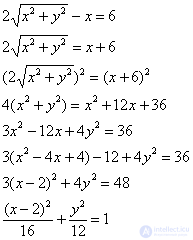
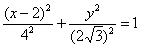– уравнение линии в прямоугольной системе координат.
3) Данная кривая представляет собой эллипс с центром симметрии в точке 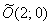, большой полуосью 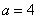и малой полуосью .

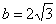Пример 9: Решение: 1) Найдем область определения функции:

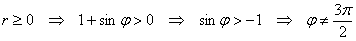
Заполним расчетную таблицу:

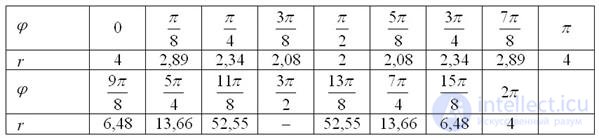
Выполним чертеж:

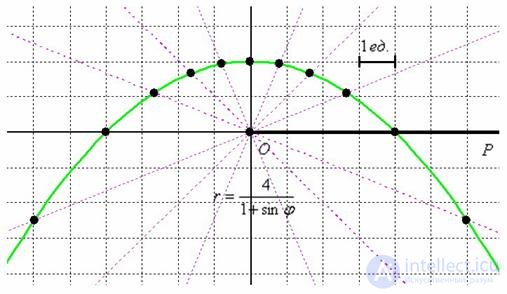
2) Найдем уравнение линии в декартовой системе координат:

Используем формулы :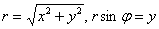

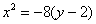– искомое уравнение. Это парабола.

3) Приведем уравнение линии к каноническому виду с помощью перехода к новой системе координат 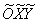, которая получается путем поворота исходной системы координат 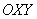на 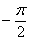рад. вокруг точки 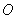и ее параллельным переносом центром в точку 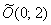(координаты – в старой системе координат).
В результате получено каноническое уравнение параболы 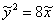, фокальный параметр которой равен 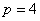. Выполним чертеж:

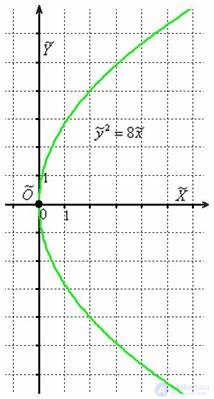
Найдем фокус: .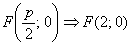
Эксцентриситет любой параболы равен единице.

Вау!! 😲 Ты еще не читал? Это зря!

• прямая в пространстве , скрещивающие прямые , параллельные прямые , каноническое уравнение прямой ,

Тебе нравиться задачи линейная алгебра? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое задачи линейная алгебра, задачи аналитическая геометрия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия