Лекция
Привет, Вы узнаете о том , что такое полубесконечная длинная линия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое полубесконечная длинная линия, линия конечной длины, отражения, режимы работы длинной линии, условия режима бегущих волн, пространственная частота сигнала , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
Решение волновых уравнений значительно упрощается, если рассматривать полубесконечную длинную линию при гармоническом воздействии e(t) = Em cosωt .
В такой линии нет условий для распространения обратной волны, а потому существует лишь прямая, ее называют падающей волной.
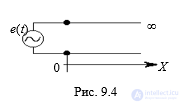
• Установившиеся процессы в такой линии в произвольном сечении являются гармоническими, но появляется фазовый сдвиг, который связан с конечной скоростью
распространения волны. Напряжение и ток в любом сечении определяются из соотношений:
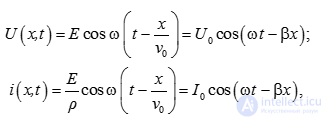
где v0 = λ/Т = (L0C0)–2 – скорость распространения сигнала в длинной линии;
• β = ω/v0 – коэффициент фазы, он характеризует фазовый сдвиг волны на единицу длины линии, иногда его называют пространственной частотой сигнала, так как β = 2π/λ , где λ – длина волны (это название дано по аналогии с тем, что ω = 2π/Т –временная частота).
• Отношение комплексной амплитуды напряжения к комплексной амплитуде тока прямой волны называют волновым сопротивлением линии Zв = Um / Im. В линии без потерь оно имеет чисто резистивный характер –ρ, его называют характеристическим сопротивлением.
(v0, β, Zв) - называются волновыми, или вторичными, параметрами длинной линии.
Т.О., в длинной линии без потерь сигнал в любом сечении не изменяет своей формы и амплитуды, но наблюдается запаздывание вследствие конечной скорости В линии с потерями наблюдается не только запаздывание во времени, но и затухание
сигнала по амплитуде с возрастанием х.
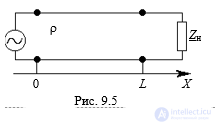
• На практике часто используются линии Zн конечной длины. Пусть однородная линия длиной L нагружена на конце (x = L) на сопротивление Zн.
При x = 0 линия питается от генератора гармонической ЭДС с внутренним сопротивлением Ri.
•Волновое сопротивление линии Zв = ρ.
• При гармоническом колебании мгновенное значение напряжения в любой точке определяется суммой падающей и отраженной волн
напряжения,
а мгновенные значения тока – разностью падающей и
отраженной волн тока. Знаки в суммах связаны с тем, что положительные направления напряжений Uпад
Uотр выбраны одинаково (сверху вниз), а у токов Iпад, Iотр – встречно, поэтому они вычитаются:
U(x,t) = Uпад+ Uотр;
I(x,t) = Iпад – Iотр,
где U(x,t),Uпад, Uотр , I(x,t) , Iпад, Iотр – комплексные амплитуды.
• Процессы, происходящие в длинной линии, определяются не только волновыми параметрами, которые характеризуют собственные свойства линии, но и коэффициентами отражения, которые зависят от согласования линии с нагрузкой.
• В установившемся режиме в линии присутствуют две волны. Об этом говорит сайт https://intellect.icu . Эти волны распространяются в двух взаимно противоположных направлениях. Волна, движущаяся от генератора к нагрузке, называется прямой, или падающей. Волна, движущаяся от нагрузки к генератору, называется обратной, или
отраженной. Появление обратной волны связано с отражением падающей волны от нагрузки. Таким образом, в длинной линии в каждый момент времени в каждой точке сечения присутствует алгебраическая сумма двух волн – падающей и отраженной.
• Комплексным коэффициентом отражения длинной линии называют отношение комплексных амплитуд напряжений и токов отраженной и падающей
волн в произвольном сечении линии:
• комплексный коэффициент отражения напряжения;
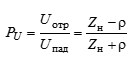
• комплексный коэффициент отражения тока.
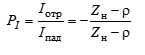
• В зависимости от соотношения волнового сопротивления ρ и сопротивления нагрузки Zн в длинной линии возможны три режима работы:
• 1. Режим бегущих волн в линии имеет место, когда в ней распространяется только падающая волна напряжения и тока, а
отраженная волна во всех сечениях равна нулю. В этом режиме вся энергия от источника питания передается в нагрузку, отражение отсутствует, следовательно, Uотр= 0 и Рu = 0.
• 2. Режим стоячих волн имеет место, когда происходит полное отражение волны от нагрузки, т.е. в линии одновременно
присутствуют две волны, амплитуды которых одинаковы: Uотр = Uпад, следовательно | Рu | = 1. В этом режиме энергия в
нагрузке не выделяется.
• 3. Режим смешанных волн. В этом режиме энергия частично выделяется в нагрузке, а частично отражается, т.е. в линии
одновременно присутствуют две волны, амплитуды которых не одинаковы.
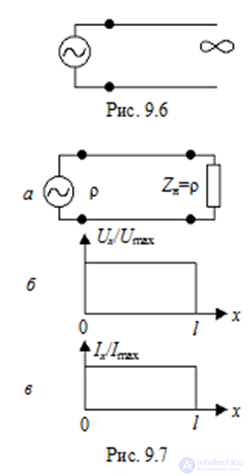
Режим бегущих волн возможен при следующих видах нагрузки:
• а) полубесконечная длинная линия (рис. 9.6). В ней нет конца, а потому и нет отраженной волны.Рис. 9.6
• б) линия нагружена на сопротивление, равное волновому Zн = ρ (рис. 9.7, а).
• Коэффициент отражения равен нулю 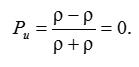
• В линии без потерь в режиме бегущих волн распределение амплитуд напряжения и тока по длине линии постоянно
(рис. 9.7, б, в), а в линии с потерями амплитуды напряжения и тока убывают по экспоненте.
• Входное сопротивление линии в режиме бегущих волн равно волновому сопротивлению линии и не зависит от ее длины.
• В режиме бегущих волн передача энергии происходит только в одном направлении – от источника сигнала в нагрузку, такая
нагрузка называется согласованной.
В этом режиме вся падающая волна отражается от нагрузки. Мощность, выделяемая на нагрузке, равна нулю. Режиме стоячих волн Рu = 1 возникает в следующих трех случаях (рис. 9.8):
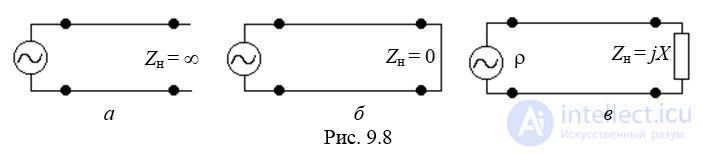
1) линия, разомкнутая на конце Zн = ∞.
2) Zн = 0
3) Zн = jX
Коэффициент отражения по напряжению Рu = 1. Это означает, что на конце линии волна по напряжению полностью отражается, т.е. амплитуда падающей волны равна амплитуде отраженной волны, причем знак отраженной волны совпадает с падающей, что приводит к удвоению напряжения на конце линии.
Коэффициент отражения по току Рi = –1. Это означает, что на конце линии ток равен нулю.
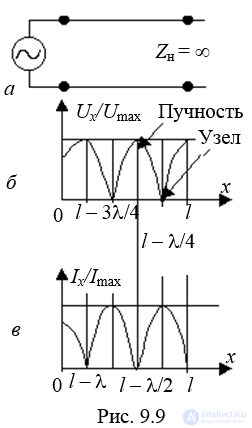
Распределение амплитуд напряжения и тока вдоль линии в режиме холостого хода приведены на рис. 9.9, б.
Точки максимума напряжения или тока называются пучностями напряжения или тока, а точки, в которых амплитуда напряжения или тока равны нулю, называются узлами.
В режиме холостого хода на конце линии имеет место пучность напряжения и узел тока.
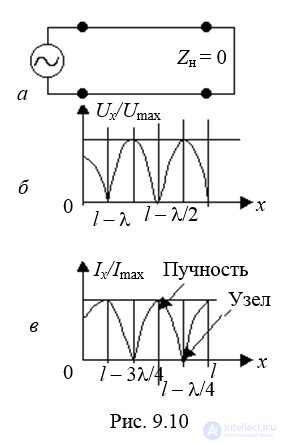
б) линия короткозамкнутая на конце: Zн = 0. Коэффициенты отражения 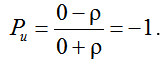 . Рi = 1.
. Рi = 1.
Графики распределения амплитуд напряжения и тока показаны на рис. 9.10, б, в. На конце линии имеет место пучность тока и узел напряжения.
в) линия нагружена на реактивное сопротивление Zн = jX.
Коэффициенты отражения 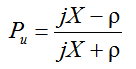 и
и 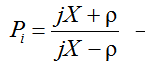 – комплексные величины, а их модули равны │Рu│=│Рi│=1. Это означает, что амплитуды прямой и отраженной волн в линии одинаковы, но на конце нет ни пучности, ни узла.
– комплексные величины, а их модули равны │Рu│=│Рi│=1. Это означает, что амплитуды прямой и отраженной волн в линии одинаковы, но на конце нет ни пучности, ни узла.
3) Режим смешанных волн.
В таком режиме падающая волна частично поглощается, а частично отражается. Он возникает в следующих случаях:
а) нагрузка – комплексное сопротивление:
Zн = Rн + jXн Um min Um max.
б) нагрузка – резистивное сопротивление, не равное волновому сопротивлению ρ:
Zн = Rн ≠ ρ.
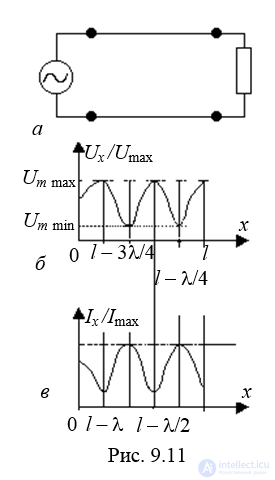
В режиме смешанных волн амплитуда отраженной волны меньше, чем амплитуда падающей. Следовательно, │Рu│=│Рi│<1, а потому амплитуды тока и напряжения в минимумах не равны нулю. На рис. 9.11, б, в приведено распределение амплитуд напряжения и тока вдоль линии в режиме смешанных волн при чисто резистивной нагрузке (Rн > ρ).
Коэффициентом отражения удобно пользоваться при теоретическом анализе, однако его трудно определить экспериментально, поскольку трудно разделить и в отдельности измерить амплитуду падающей и отраженной волн. Поэтому на практике режимы работы длинной линии и степень ее согласования с нагрузкой характеризуют коэффициентами:
1) Коэффициент бегущей волны (КБВ):
КБВ = Um min/Um max,
где Um min, Um max – минимальное и максимальное значения амплитуды напряжения по длине линии.
2) Коэффициент стоячей волны (КСВ):
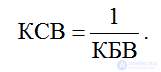 .
.
В режиме бегущих волн КБВ = 1, КСВ = 1.
В режиме стоячих волн КБВ = 0, КСВ = ∞
В режиме смешанных волн 0 < КБВ < 1, 1 < КСВ < ∞.
Исследование, описанное в статье про полубесконечная длинная линия, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое полубесконечная длинная линия, линия конечной длины, отражения, режимы работы длинной линии, условия режима бегущих волн, пространственная частота сигнала и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Комментарии
Оставить комментарий
Теоретические основы электротехники
Термины: Теоретические основы электротехники