Привет, Вы узнаете о том , что такое объемное напряженное состояние, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое объемное напряженное состояние , настоятельно рекомендую прочитать все из категории Сопротивление материалов.

9.4.1. Понятие о тензоре напряжений. Экстремальные касательные напряжения

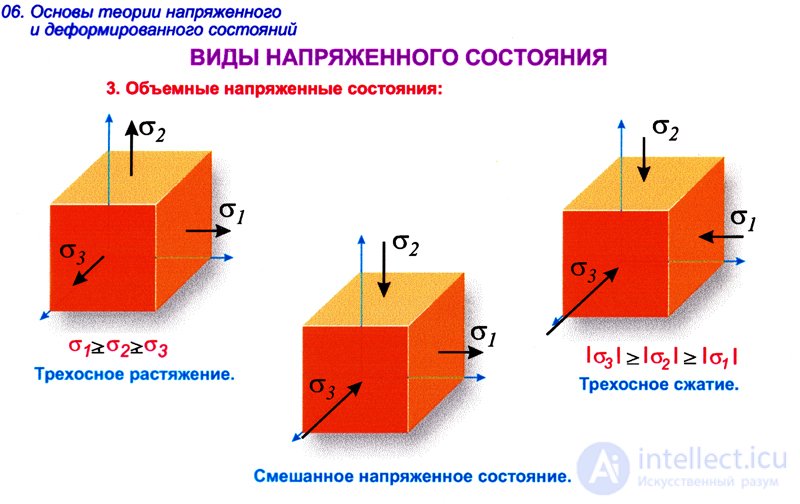
Случай объемного напряженного состояния представлен на рис.9.2. Как уже отмечалось у разделе 9.1 настоящего пособия, на каждой из граней действует нормальное напряжение 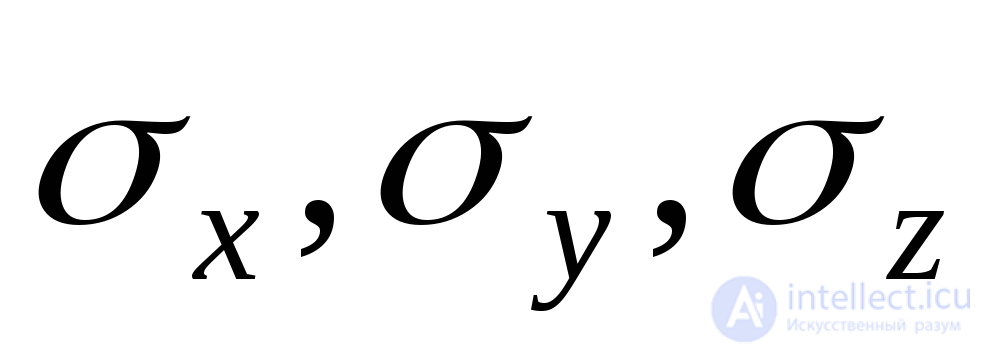, а также по две составляющие касательного напряжения.

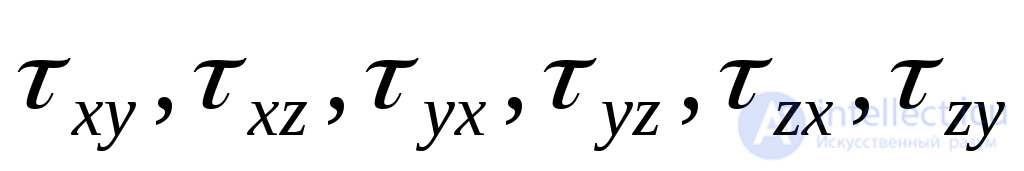Таким образом, напряженное состояние в выделенном элементарном параллелепипеде в общем случае характеризуется девятью компонентами напряжений, которые могут быть записаны в виде тензора напряжений:

. (9.25)

Касательные напряжения, представленные тензором напряжения, связаны рядом зависимостей, получить которые можно, составив уравнение суммы моментов всех сил относительно координатных осей 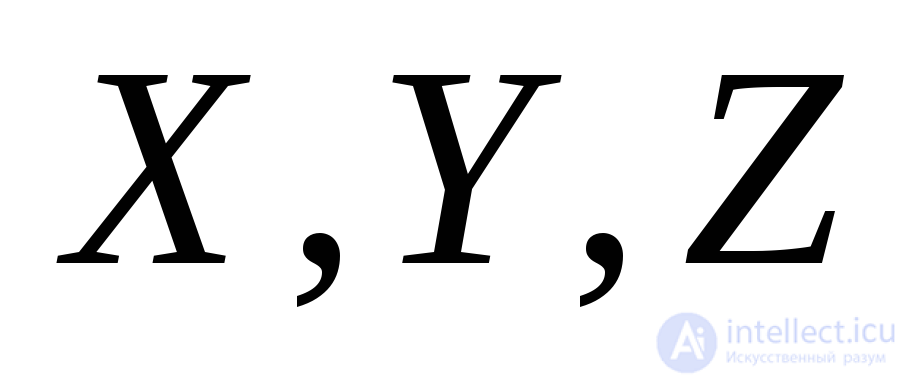(Рис.9.2):

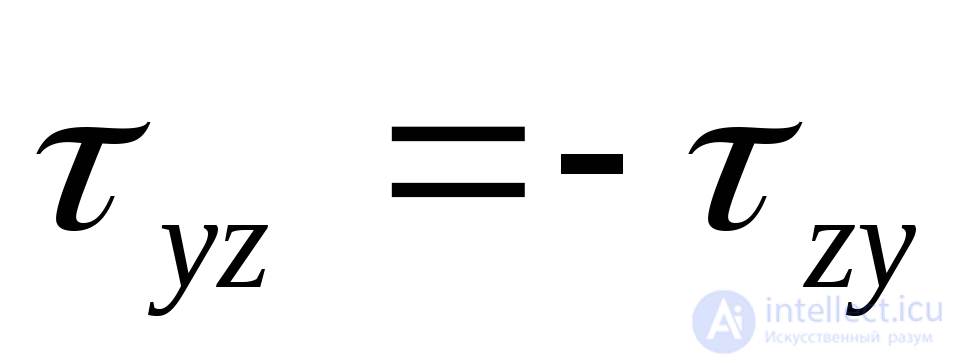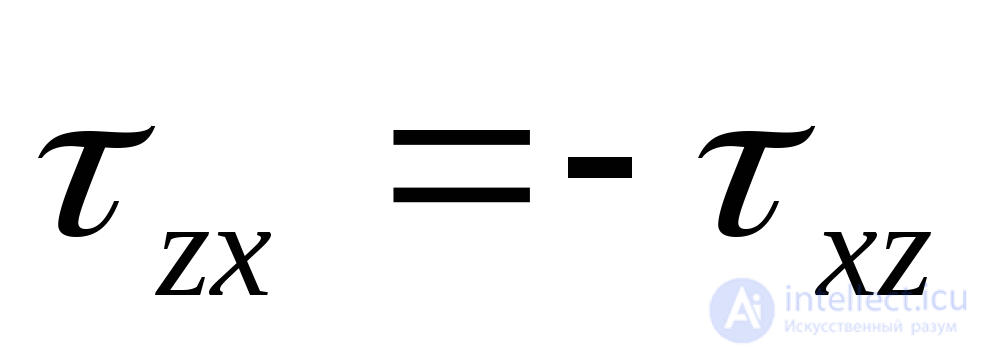;;. (9.26)

Модули этих напряжений одинаковы, а знаки на основании закона парности касательных напряжений (9.8) противоположны.

Общий случай напряженного состояния (Рис.9.19а) может быть представлен в виде суммы двух напряженных состояний, характеризуемых в первом случае одинаковыми нормальными напряжениями 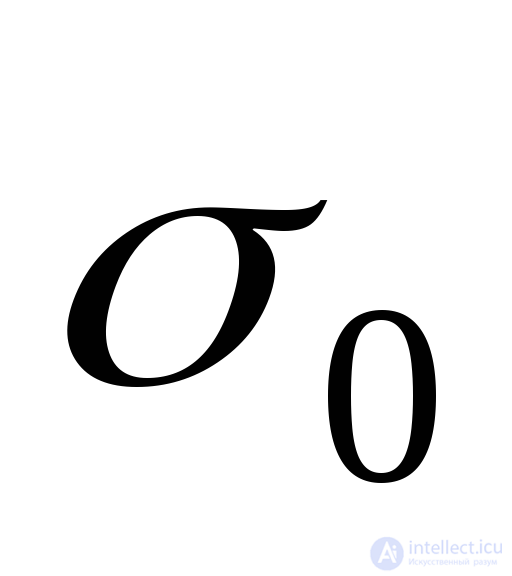(Рис.9.19,б) и во втором случае (Рис.9.19,в) – нормальными напряжениями:

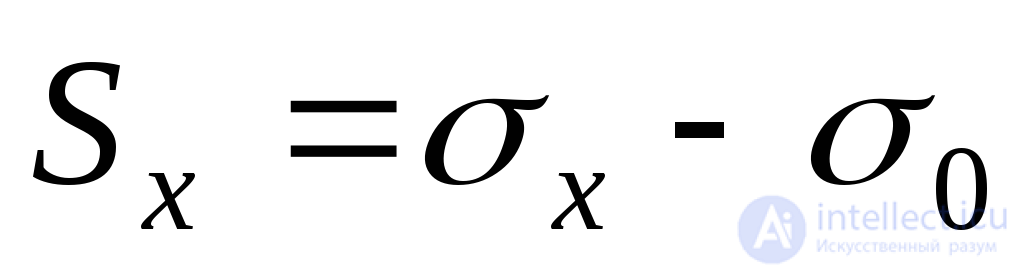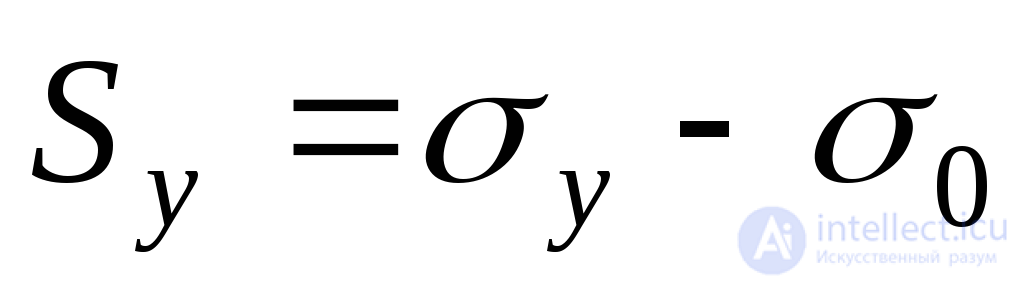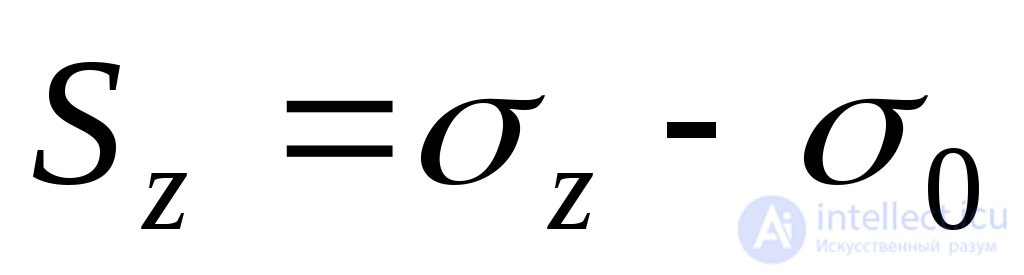;;(9.27)

и касательными напряжениями .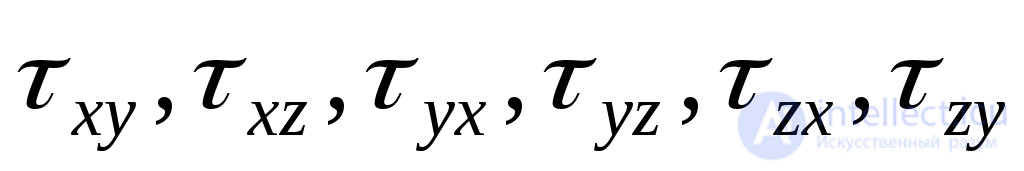

Рис.9.19

Примем:

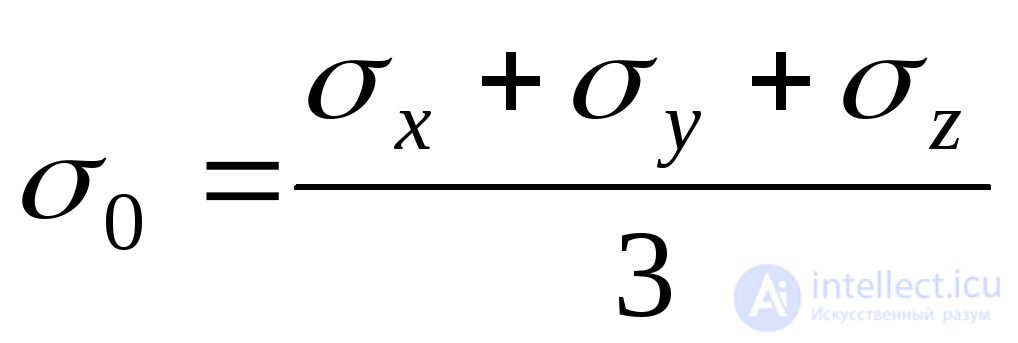. (9.28)

Тогда из (9.27) следует:

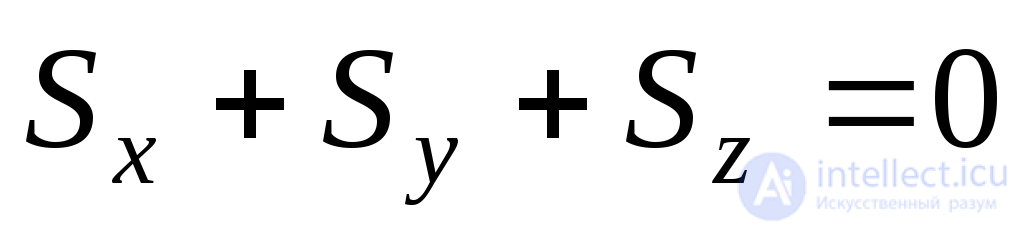. (9.29)

Напряженное состояние, представленное на рис.9.19,б, может быть описано шаровым тензором напряжений:

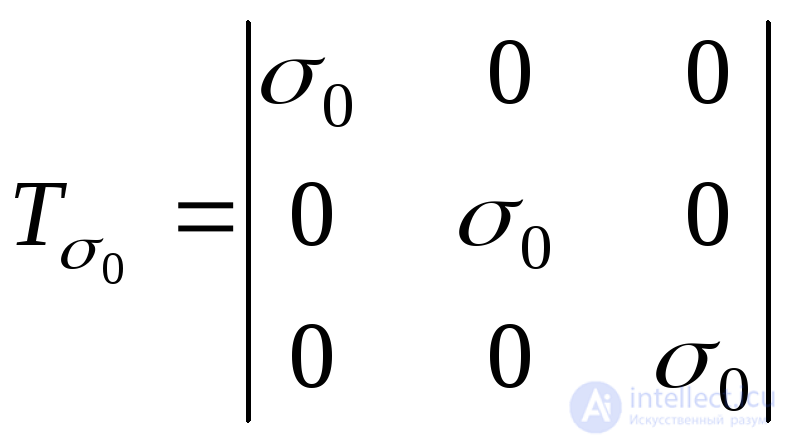. (9.30)

Напряженное состояние, представленное на рис.9.19,в, может быть описано тензором, который назывется девиатором напряжений:

. (9.31)

Шаровой тензор характеризует изменение объемавыделенного элемента, девиатор характеризует изменениеформыэлемента.

Рассмотрим определение главных напряжений и, через напряжения, действующие на произвольных площадках (Рис.9.19,а). Предположим, что нам известно положение главной площадки, определяемое наклоном нормали к этой площадкепо отношению к осям координат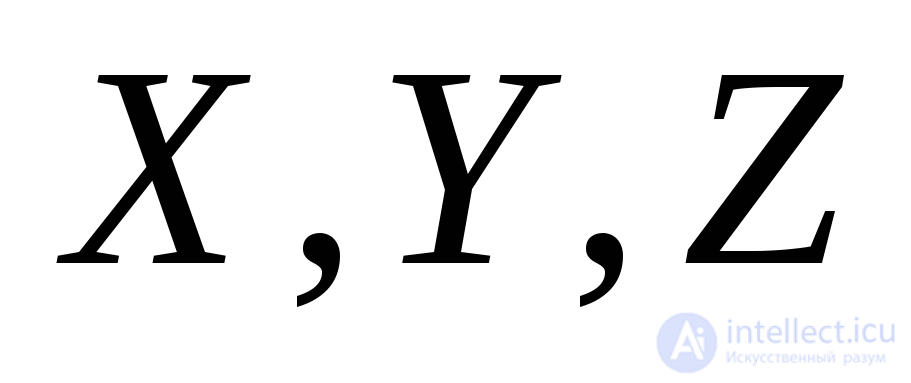. Сечением, параллельным этой площадке, выделим из исходного параллелепипеда тетраэдр, изображенный на рис.9.20, и составим условия равновесия тетраэдра в виде сумм проекций всех действующих сил на оси координат.

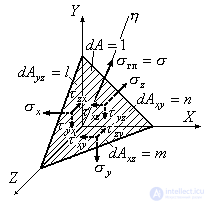
Рис.9.20

Косинусы углов, образованные нормалью с осями координат, обозначим соответственно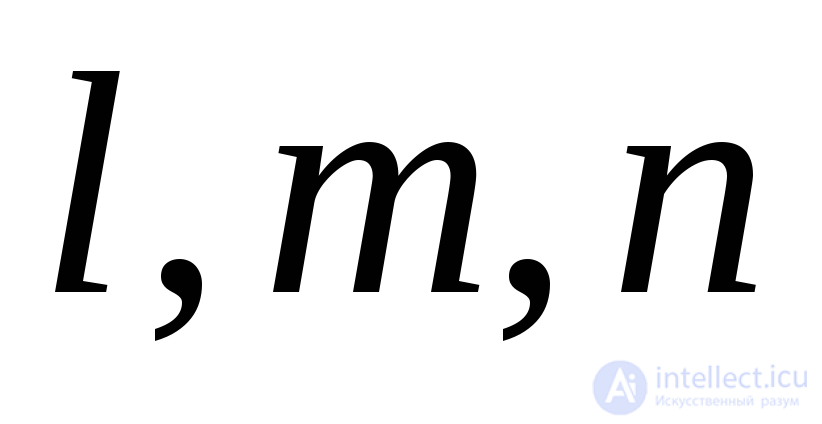. Примем площадь наклонной грани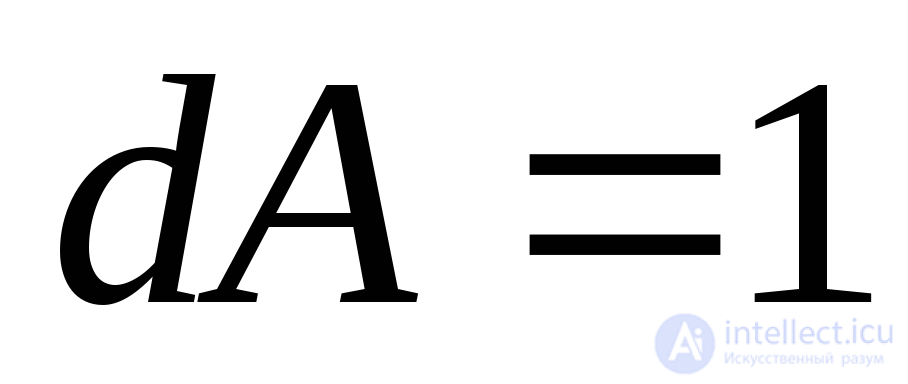, тогда площади других граней, лежащих в координатных плоскостях, будут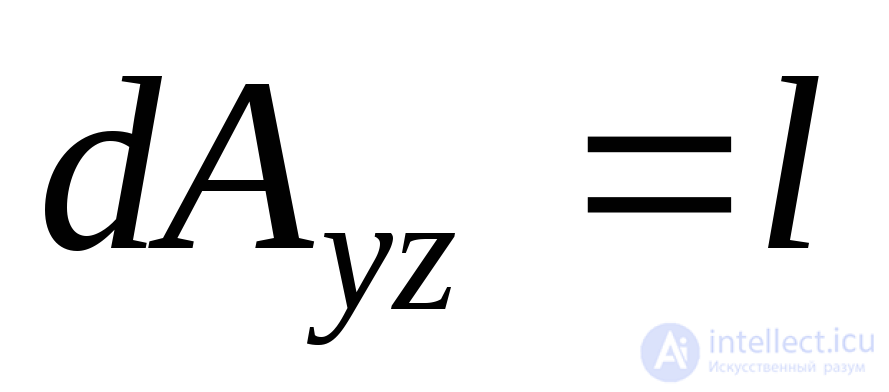,,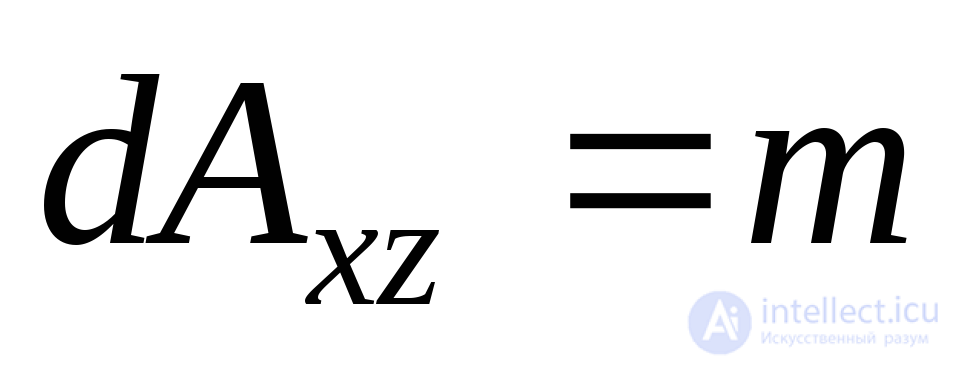. На главной площадке касательные напряжения отсутствуют. Действующее здесь главное напряжениеобозначим. Сумма проекций сил на ось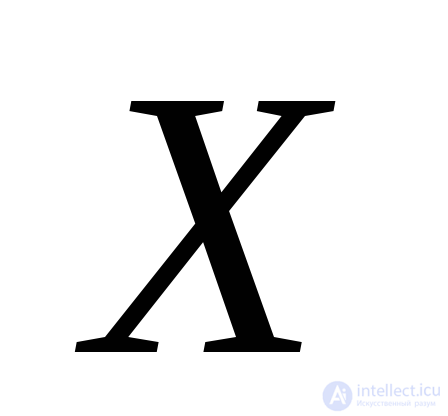дает:

.

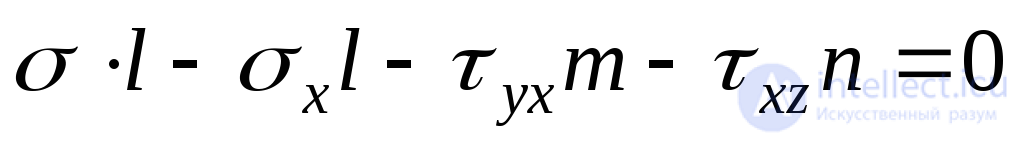Проектируя все силы на оси и, получим еще два аналогичные уравнения. Таким образом, будем иметь следующие три уравнения равновесия тетраэдра:

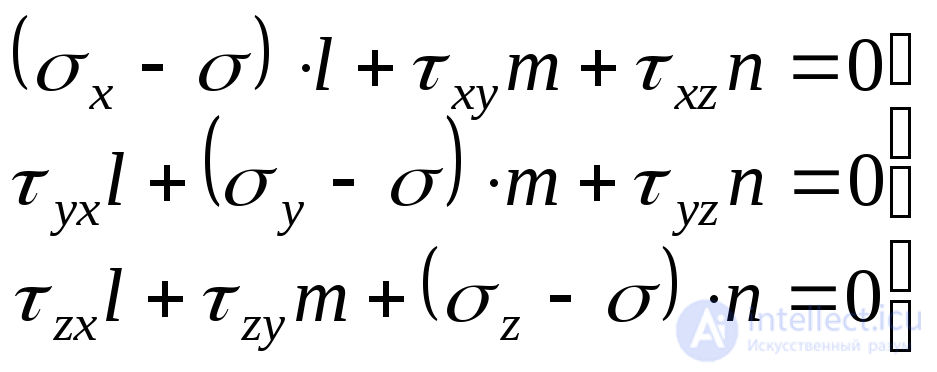. Об этом говорит сайт https://intellect.icu . (9.32)

Уравнения (9.32) можно рассматривать как однородную систему уравнений относительно неизвестных 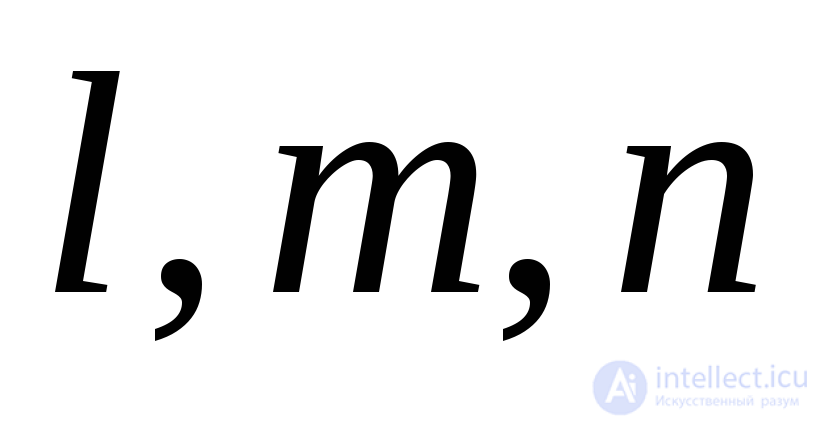. Между направляющими косинусами нормалисуществует зависимость

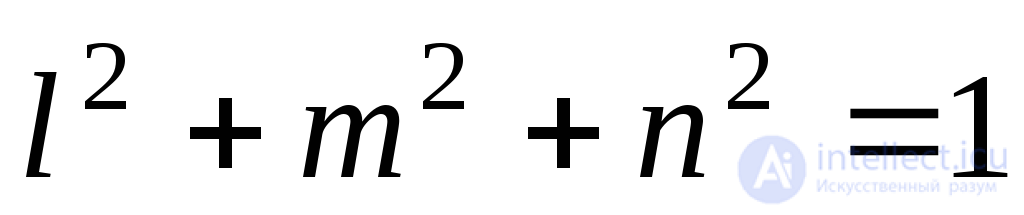, (9.33)

поэтому они не могут одовременно равняться нулю. Известно, что при этом условии определитель системы (9.32) должен быть равен нулю, т.е.

. (9.34)

Раскрыв определитель (9.43), придем к кубическому уравнению:

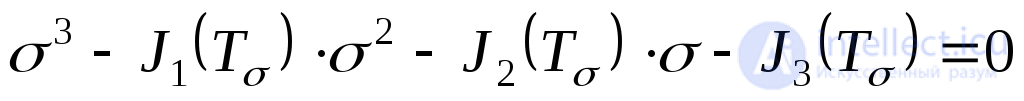, (9.35)

три корня которого представляют сосбой главные напряжения .

Коэффициенты уравнения (9.35) принимают вид:

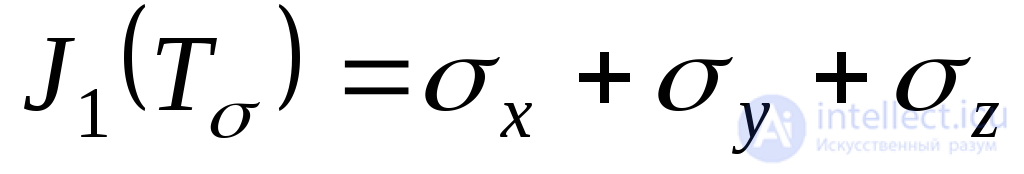; (9.36)

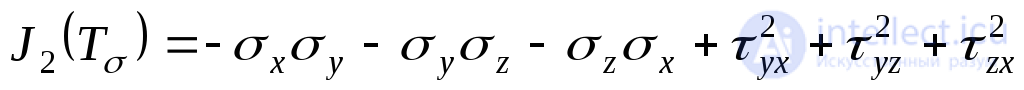;(9.37)

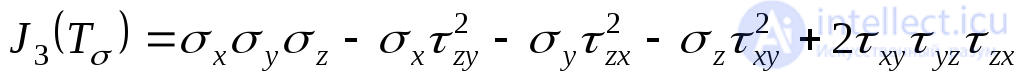.(9.38)

Поскольку главные напряжения не зависят от выбора осей координат, коэффициенты кубического уранения (9.35) также не изменяются при повороте осей координат, т.е. являются инвариантамии называются соответственно, первым, вторыми третьим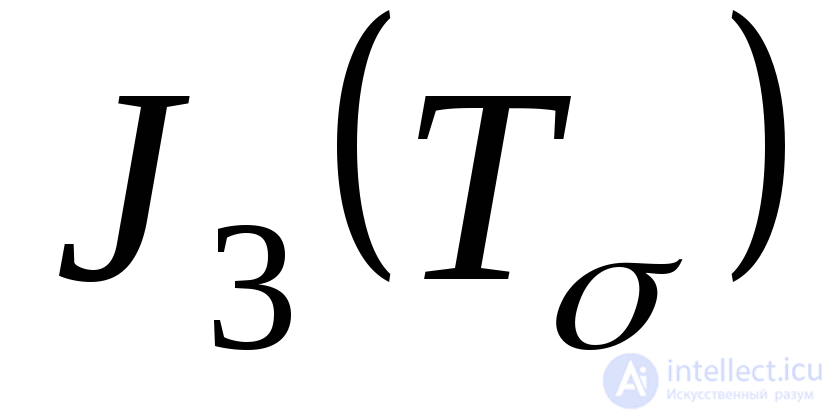инвариантами тензора напряжений. Из формул (9.36)-(9.38) следует, что выражения инвариантов тензора напряжений через главные напряжения имеют вид:

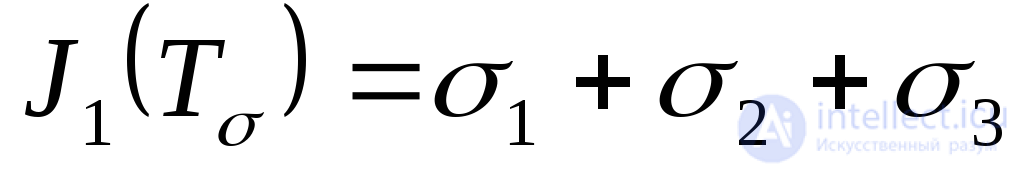; (9.39)

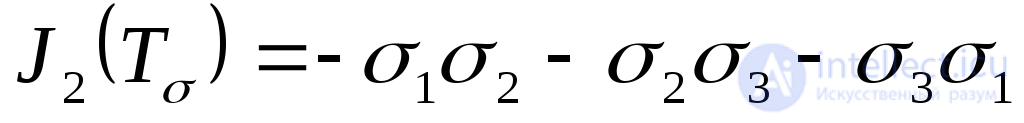;(9.40)

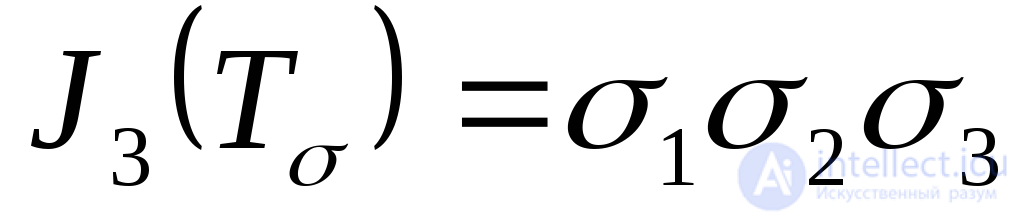.(9.41)

В частном случае плоского напряженного состояния кубическое уравнение (9.35) сводится к квадратному, два корня которого дают значения и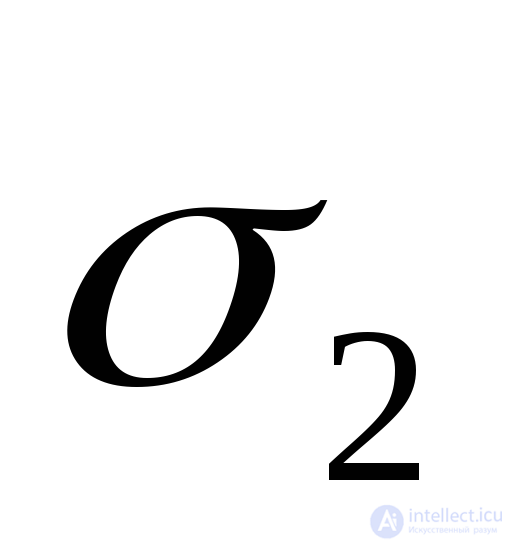, совпадающими с формулами (9.19), полученными выше. В этом случае нужно положить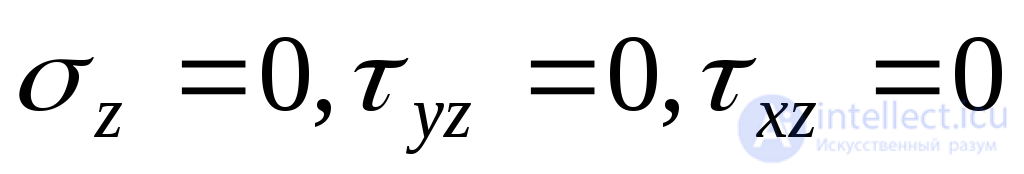, так как граньисходного параллелепипеда должна быть свободна от напряжений.

Для определения направляющих косинусов 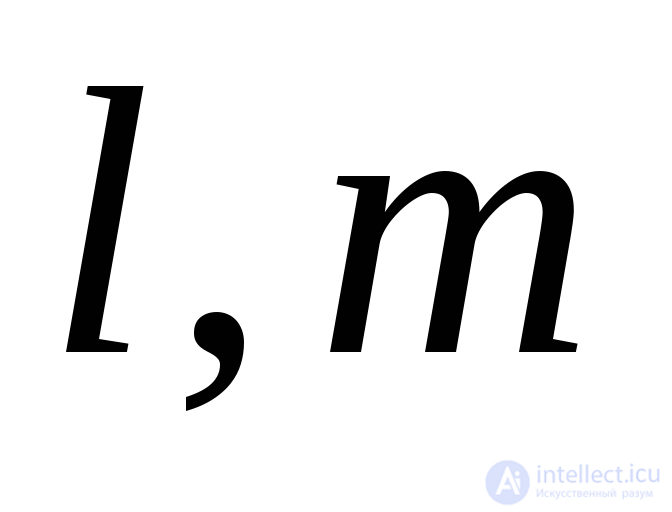и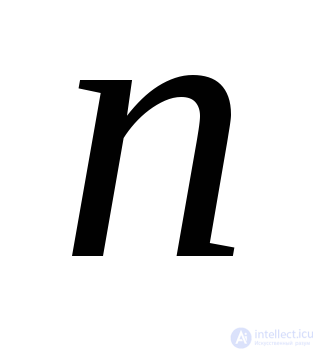, соответствующих одному из трех главных напряженийи, нужно значение этого главного напряжения подставить в выражение (9.32) вместо. Совместное решение уравнений (9.32) даст искомые величиныи.

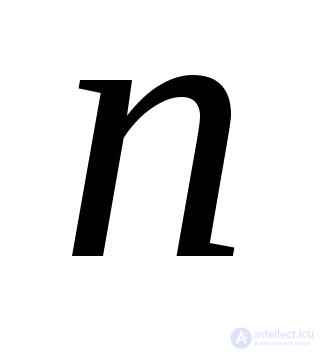Для определения максимальных касательных напряжений примем, что главные напряжения 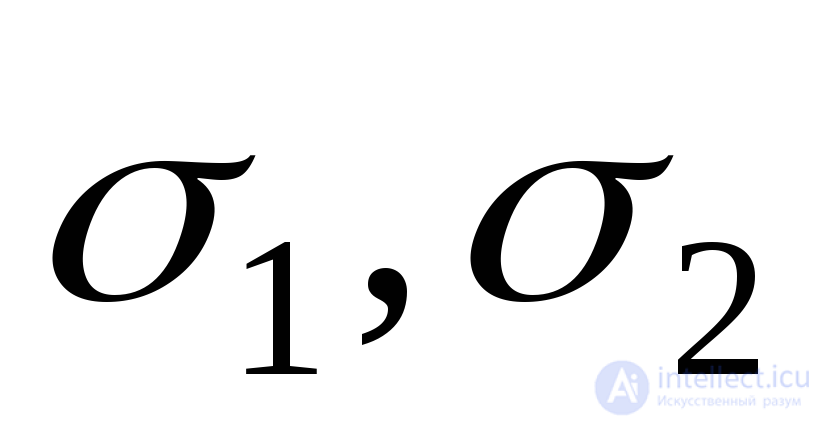иизвестны. Как и при плоском напряженном состоянии максимальные каксательные напряжения действуют в площадках, наклоненных под углом 450к главным напряжениям. Касательные напряжения на этих площадках будут иметь вид:

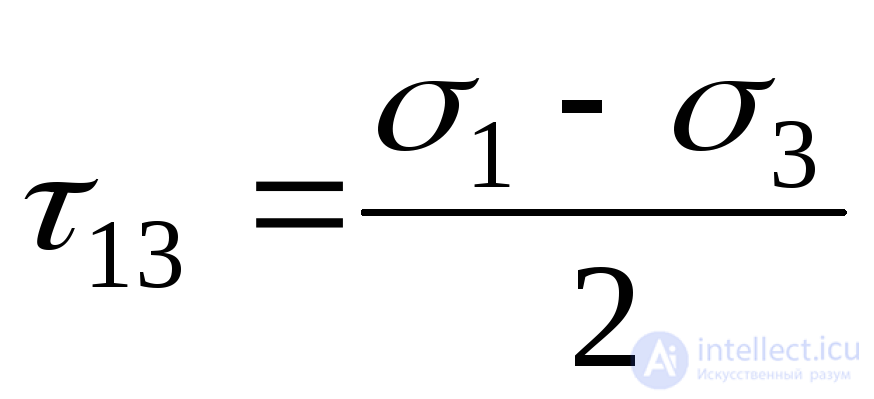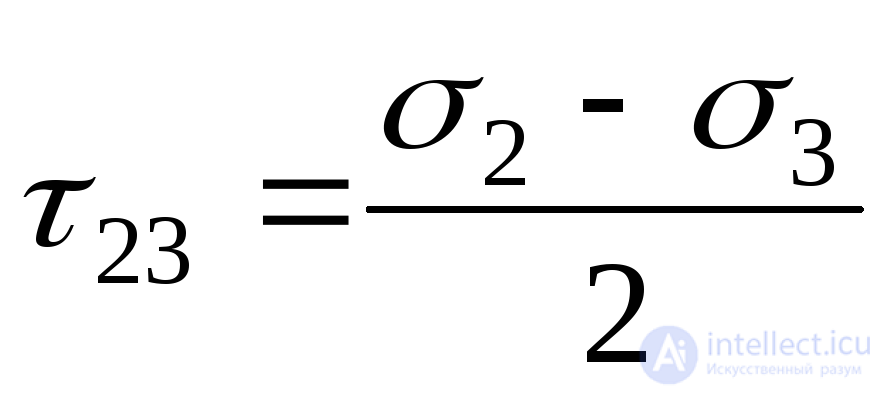;;. (9.42)

Наибольшее из этих напряжений определяет максимальные касательные напряжения в точке:

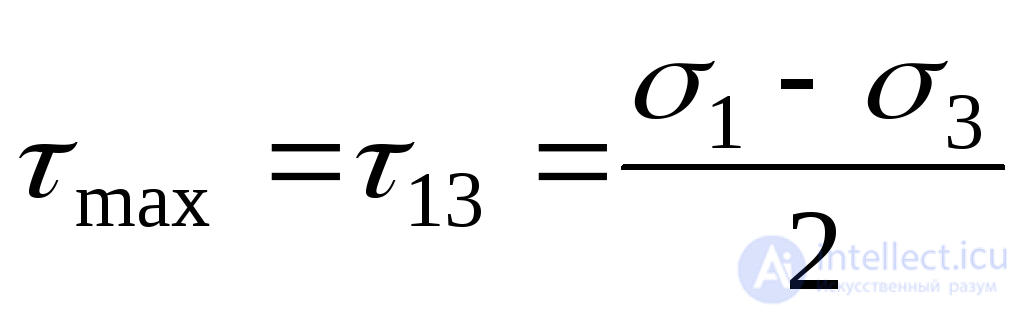. (9.43)

Таким образом, в общем случае максимальное касательное напряжение в точке действует на площадке, наклоненной под углом 450 к максимальному и минимальному из трех главных напряжений, и равно их полуразности.

Прочность материала или переход его под нагрузкой в пластическое состояние в ряде случаев связывают с величиной максимального касательного напряжения , и поэтому оно наряду с главными напряжениями является важной характеристикой напряженного состояния.

9.4.2. Напряжения на произвольно наклоненных площадках

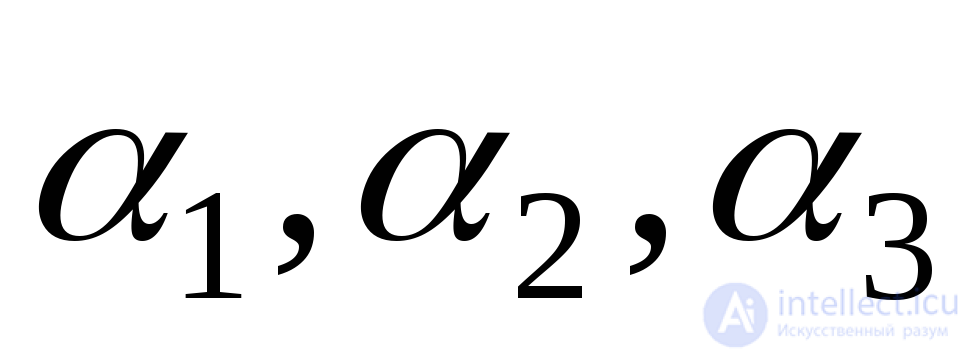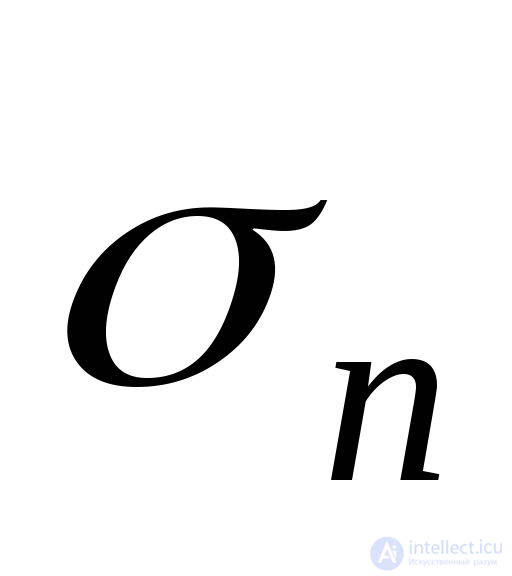Получим формулы для напряжений и, действующих на произвольно ориентированной площадке, Положение этой площадки определим углами, образованными нормальюк этой площадке с осями 1, 2 и 3, соответственно параллельными главным напряжениями. Формулы для напряженийи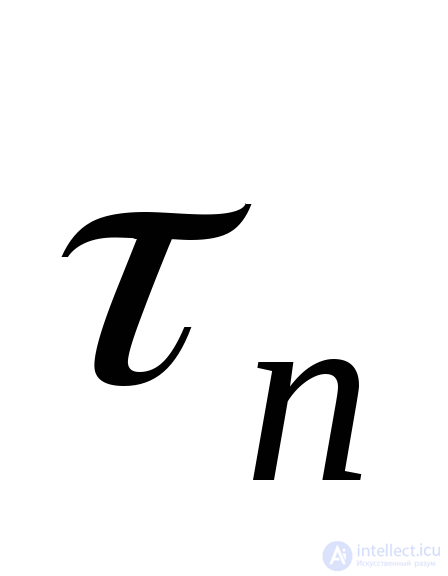получим из условия равновесия элементарного четырехгранника (тетраэдра), приведенного на рис.9.21, выделенного из главного параллелепипеда.

Рис.9.21

Примем площадь 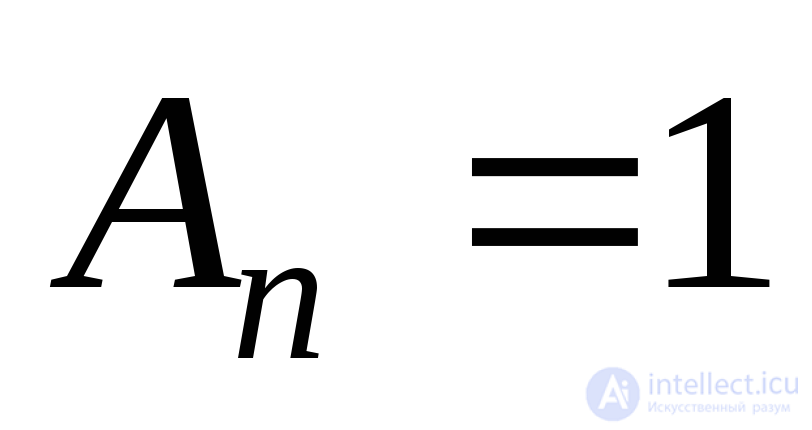, тогда площади других граней тетраэдра как проекции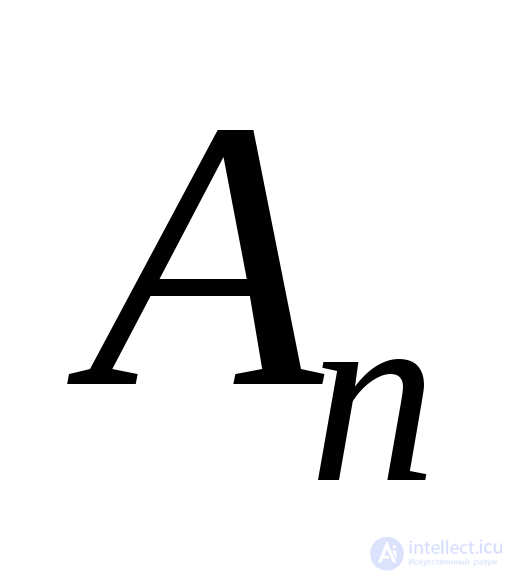на координатные плоскости примут вид:

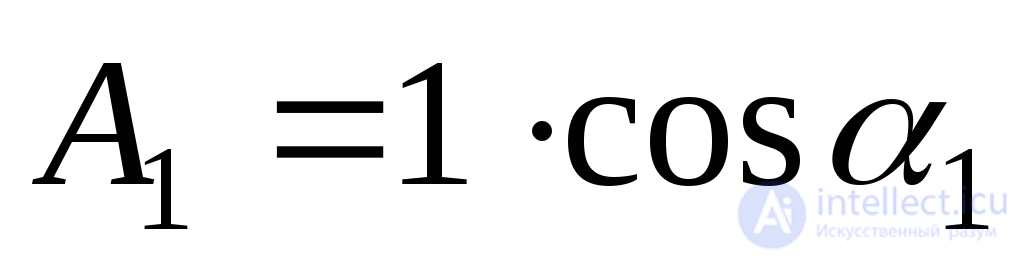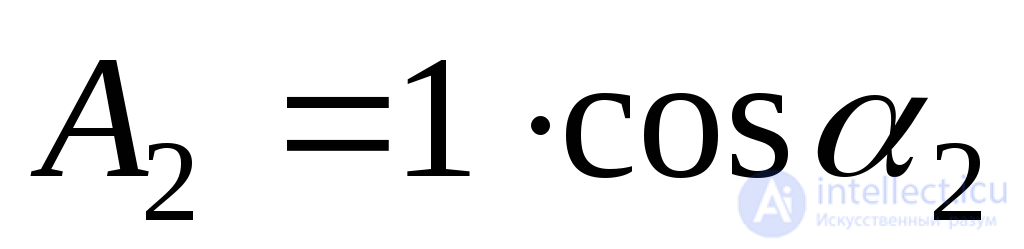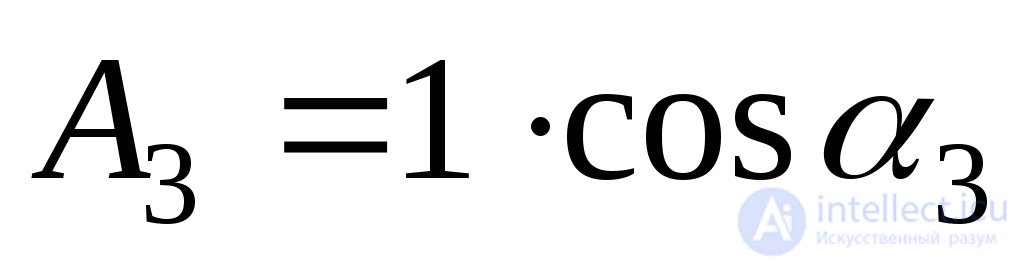;;. (9.44)

Проектируя все силы на нормаль 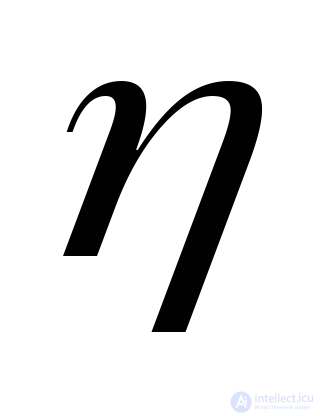, найдем

, (9.45)

откуда, учитывая (9.44), получим формулу для нормального напряжения:

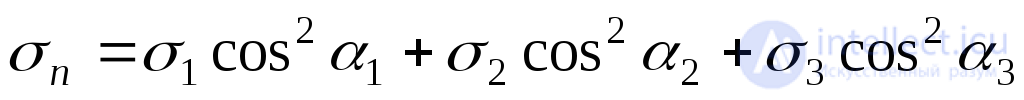. (9.46)

Так как нам неизвестно направление касательного напряжения 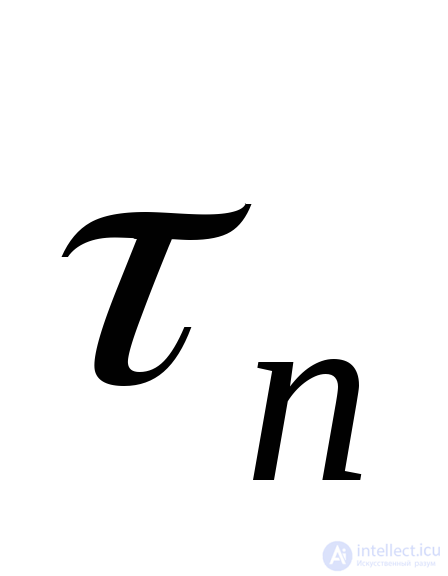, то найдем прежде полное напряжение.

Если в пространстве построить многоугольник сил, действующих на тетраэдр, то вектор будет диагональю параллелепипеда, у которого ребра равны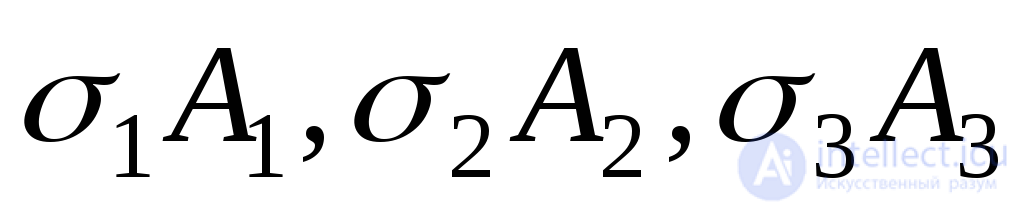. Таким образом:

.

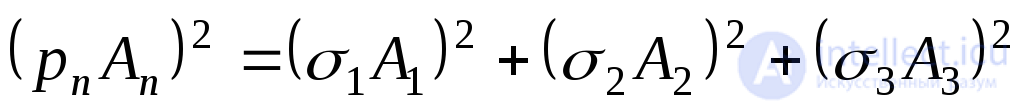Отсуда, используя (9.44), получим полное напряжение:

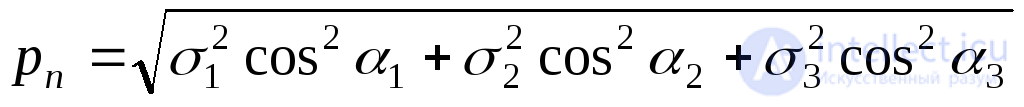. (9.47)

Теперь можно определить касательное напряжение:

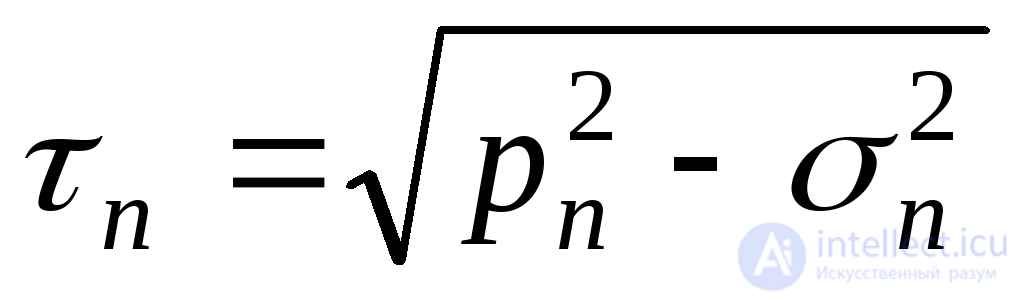. (9.48)

Формулы (9.46)-(9.48) показывают, что три главных напряжения 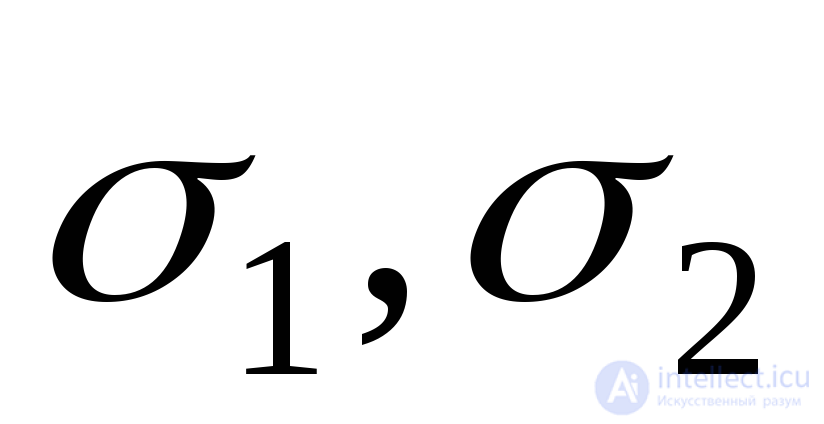ивполне определяют объемное напряженное состояние .

9.4.3. Октаэдрических напряжения. Понятие об интенсивности напряжений

Площадка, равнонаклоненная к направлению трех главных напряжений, называется октаэдрической, а действующие на ней напряжения –октаэдрическими напряжениями. Указанные площадки отсекают на осях 1,2 и 3 равные отрезки и образуют в простроанстве восьмигранник – октаэдр (Рис.9.22).

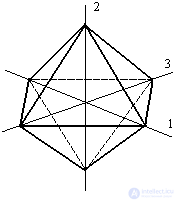
Рис.9.22

Косинусы углов 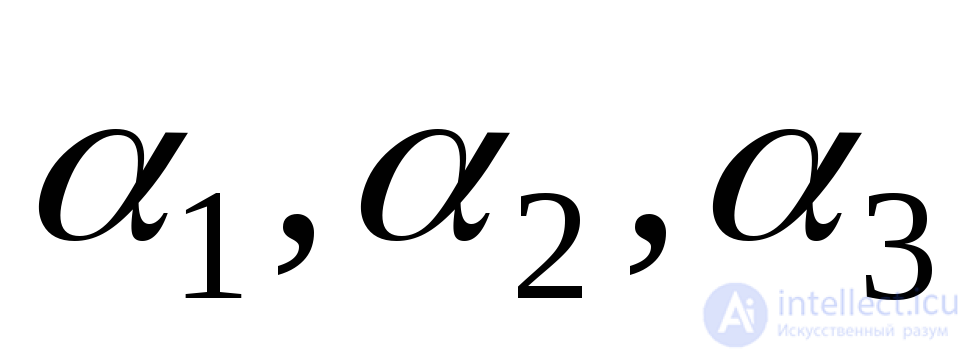являются направляющими косинусами для нормали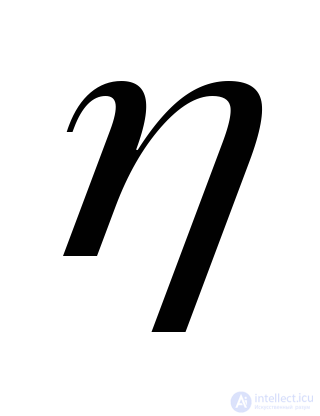и поэтому связаны соотношением:

.

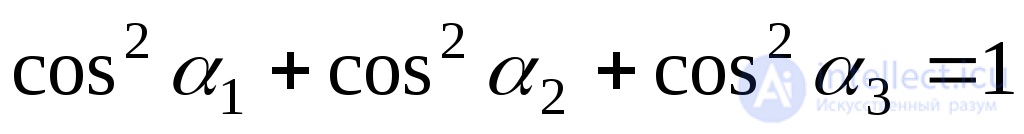Для октаэдрических площадок и, следовательно,

.

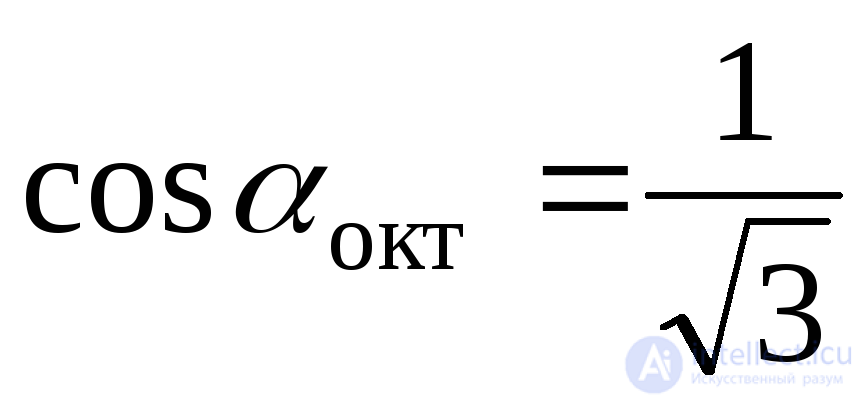Подставляя это значение косинусов в (9.46) и (9.47), найдем:

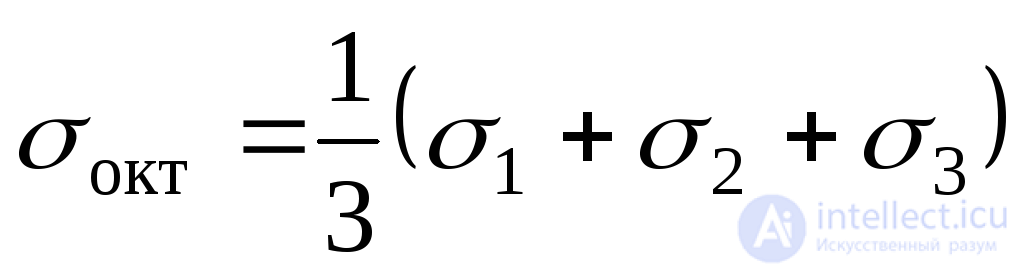. (9.49)

. (9.50)

По формуле (9.48)

.

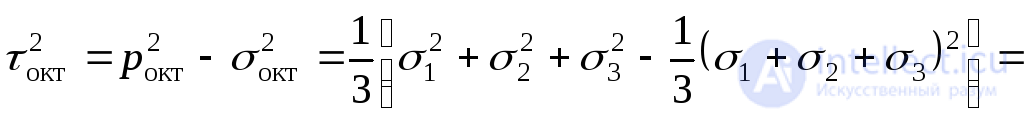
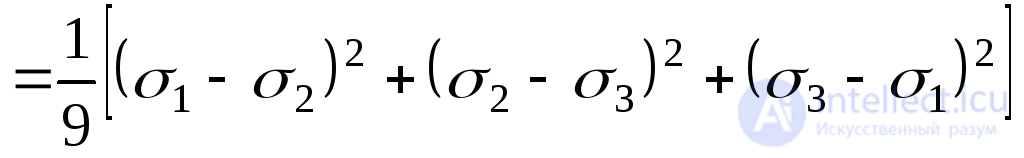Отсюда окончательно имеем:

. (9.51)

При изучении вопросов прочности тел общая деформация материала в окрестности точки подразделяется на деформации измененеия объема и формы. Важное значение октаэдрических напряжений определяется тем, что с первой из этих деформаций связано напряжение , а со второй.

Зная касательные октаэдрические напряжения, можно рассчитать интенсивностьнапряжений:

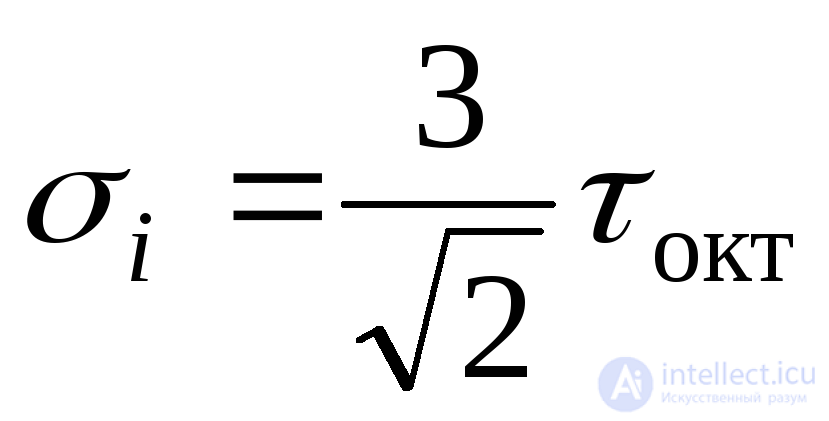(9.52)

или

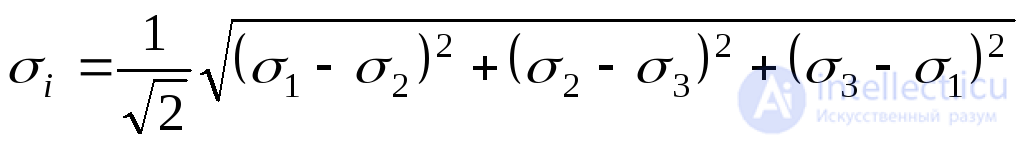(9.53)

применение

Объемное напряженное состояние материалов находит применение в различных областях, где важно учитывать трехмерное распределение напряжений и деформаций. Вот некоторые из ключевых областей применения:

1. Аэрокосмическая инженерия

• Проектирование и анализ конструкций самолетов и космических аппаратов: Объемные напряжения учитываются при моделировании нагрузок на фюзеляж, крылья и другие критические элементы конструкций, особенно при воздействии высоких температур и давлений.

2. Механическая инженерия

• Анализ и проектирование машин и механизмов: Инженеры используют модели объемного напряженного состояния для проектирования двигателей, редукторов и других компонентов, подверженных сложным нагрузкам.

3. Гражданское строительство

• Проектирование многоэтажных зданий и мостов: При проектировании устойчивых и безопасных конструкций учитываются объемные напряжения в элементах зданий и мостов.

4. Материаловедение

• Исследование и разработка новых материалов: Анализ объемного напряженного состояния помогает понять поведение материалов под сложными условиями, такими как высокие давления и температуры.

5. Геотехническая инженерия

• Анализ устойчивости грунтов и подземных сооружений: Объемное напряженное состояние грунтов и скальных пород учитывается при проектировании туннелей, фундаментов и других подземных конструкций.

6. Автомобильная промышленность

• Проектирование кузовов автомобилей и других компонентов: Модели объемного напряженного состояния используются для повышения прочности и безопасности автомобилей.

7. Нефтегазовая промышленность

• Проектирование трубопроводов и резервуаров: Объемные напряжения учитываются при анализе долговечности и надежности трубопроводов и резервуаров для транспортировки и хранения нефти и газа.

8. Биомедицинская инженерия

• Проектирование медицинских имплантов и протезов: Исследование объемного напряженного состояния в тканях и материалах имплантов помогает создавать более надежные и безопасные медицинские устройства.

Эти области показывают, насколько важно учитывать объемное напряженное состояние для обеспечения надежности и безопасности различных инженерных и технических решений.

Анализ данных, представленных в статье про объемное напряженное состояние, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое объемное напряженное состояние и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Сопротивление материалов

Из статьи мы узнали кратко, но содержательно про объемное напряженное состояние