Лекция
Привет, Вы узнаете о том , что такое магнитное поле в веществе, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое магнитное поле в веществе, диамагнетизм, парамагнетизм, молекулярные токи, напряженность магнитного поля, магнитная проницаемость , настоятельно рекомендую прочитать все из категории Базовая физика.
|
Магнетиками называются вещества, меняющие свое состояние во внешнем магнитном поле таким образом, что они сами становятся источниками магнитного поля. |
По существу все вещества в природе являются магнетиками. Иными словами, во время пребывания во внешнем магнитном поле всякое вещество намагничивается, само становясь источником магнитного поля. В некоторых случаях намагниченность сохраняется и после выключения внешнего магнитного поля — так называемые постоянные магниты. Интенсивность «отклика» различных веществ на воздействие внешнего магнитного поля отличается на многие порядки величины. Поэтому, несмотря на сказанное выше, некоторые вещества (алюминий, медь, дерево и др.) называют немагнитными. Ближайшая задача — разобраться в механизмах воздействия магнитного поля на вещество (магнетики).
В присутствии магнетика вектор магнитной индукции 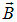 равен сумме векторов магнитной индукции внешнего магнитного поля
равен сумме векторов магнитной индукции внешнего магнитного поля 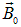 , создаваемого независимыми от магнетика токами, и магнитной индукции собственного поля магнетика
, создаваемого независимыми от магнетика токами, и магнитной индукции собственного поля магнетика 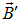
|
|
(7.1) |
Поле 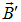 , создаваемое намагниченным магнетиком, разумеется, зависит от того, как намагничен магнетик, а намагничивается он суммарным полем
, создаваемое намагниченным магнетиком, разумеется, зависит от того, как намагничен магнетик, а намагничивается он суммарным полем 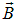 , поэтому
, поэтому 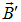 само является функцией
само является функцией 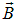 :
: 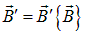 . Исключением в этом смысле может быть постоянный магнит, намагниченность которого не зависит, или практически не зависит от наличия или отсутствия внешнего магнитного поля, в частности, такое вещество, которое может оставаться намагниченным и в отсутствие внешнего — намагничивающего — поля.
. Исключением в этом смысле может быть постоянный магнит, намагниченность которого не зависит, или практически не зависит от наличия или отсутствия внешнего магнитного поля, в частности, такое вещество, которое может оставаться намагниченным и в отсутствие внешнего — намагничивающего — поля.
Далее будет показано, что если магнитное поле вне магнетика параллельно его поверхности, то поле 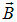 связано с магнитной индукцией
связано с магнитной индукцией 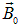 в вакууме (то есть в отсутствие магнетика) соотношением
в вакууме (то есть в отсутствие магнетика) соотношением
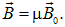
Безразмерная величина m называется магнитной проницаемостью.
Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией B и напряженностью магнитного поля H в веществе.
Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая ее состав, состояние, температуру и т. д.).
Обычно обозначается греческой буквой μ. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).
Впервые этот термин встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») опубликованной в 1881 году.
Соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как:
,
и μ в общем случае здесь следует понимать как тензор, что в компонентной записи имеет вид :
.
Для изотропных веществ запись означает умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру).
Через μ0 обозначена магнитная постоянная. В гауссовой системе эта постоянная безразмерна и равна 1, а в Международной системе единиц (СИ)
Гн/м (Н/А2). Магнитная проницаемость μ в обеих системах единиц является безразмерной величиной. Иногда при пользовании СИ произведение μ0μ
именуют абсолютной, а коэффициент μ — относительной магнитной проницаемостью.
Величина магнитной проницаемости отражает, насколько массово магнитные моменты отдельных атомов или молекул данной среды ориентируются параллельно приложенному внешнему магнитному полю некоей стандартной напряженности и насколько велики эти моменты. Значениям μ близким к 1 соответствует слабая ориентированность моментов (почти хаос в направлениях, как без поля) и их малость, а далеким от 1, наоборот, высокая упорядоченность и большие величины или большое число индивидуальных магнитных моментов.
Есть аналогия с содержанием понятия «диэлектрическая проницаемость» как показателя меры реагирования электрических дипольных моментов молекул на электрическое поле.
Магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением:
μ=1+χ ,
а в гауссовой системе аналогичное соотношение выглядит как
μ=1+4πχ .
Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля для анизотропных веществ (и, кроме того, от температуры, давления и т. д.).
Также она зависит от скорости изменения поля со временем, в частности, для синусоидального изменения поля — зависит от частоты этого колебания (в этом случае для описания намагничивания вводят комплексную магнитную проницаемость, чтобы описать влияние вещества на сдвиг фазы B относительно H). При достаточно низких частотах — небольшой быстроте изменения поля, ее можно обычно считать в этом смысле независимой от частоты.
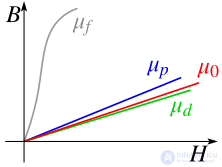
Схематический график зависимости 'B' от 'H' (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ0) и диамагнетиков (μd)
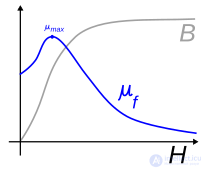
Кривая намагничивания для ферромагнетиков (и ферримагнетиков) и соответствующий ей график магнитной проницаемости
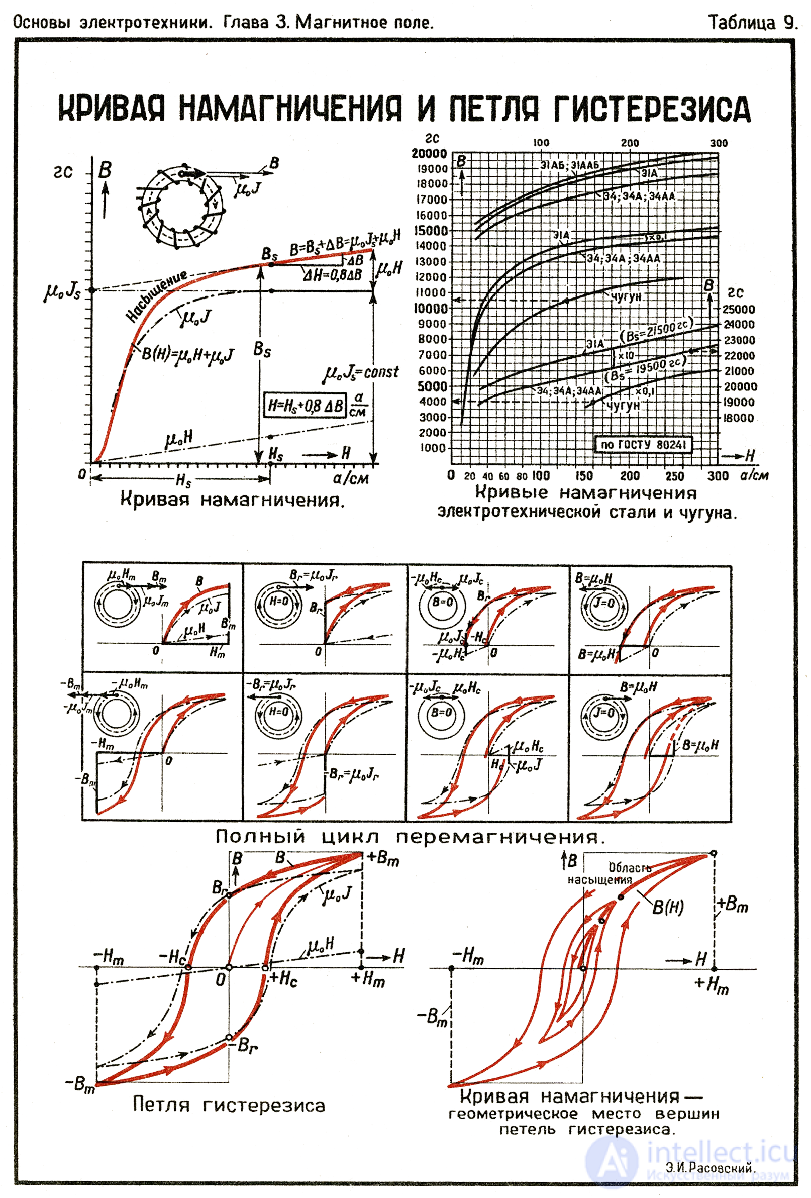
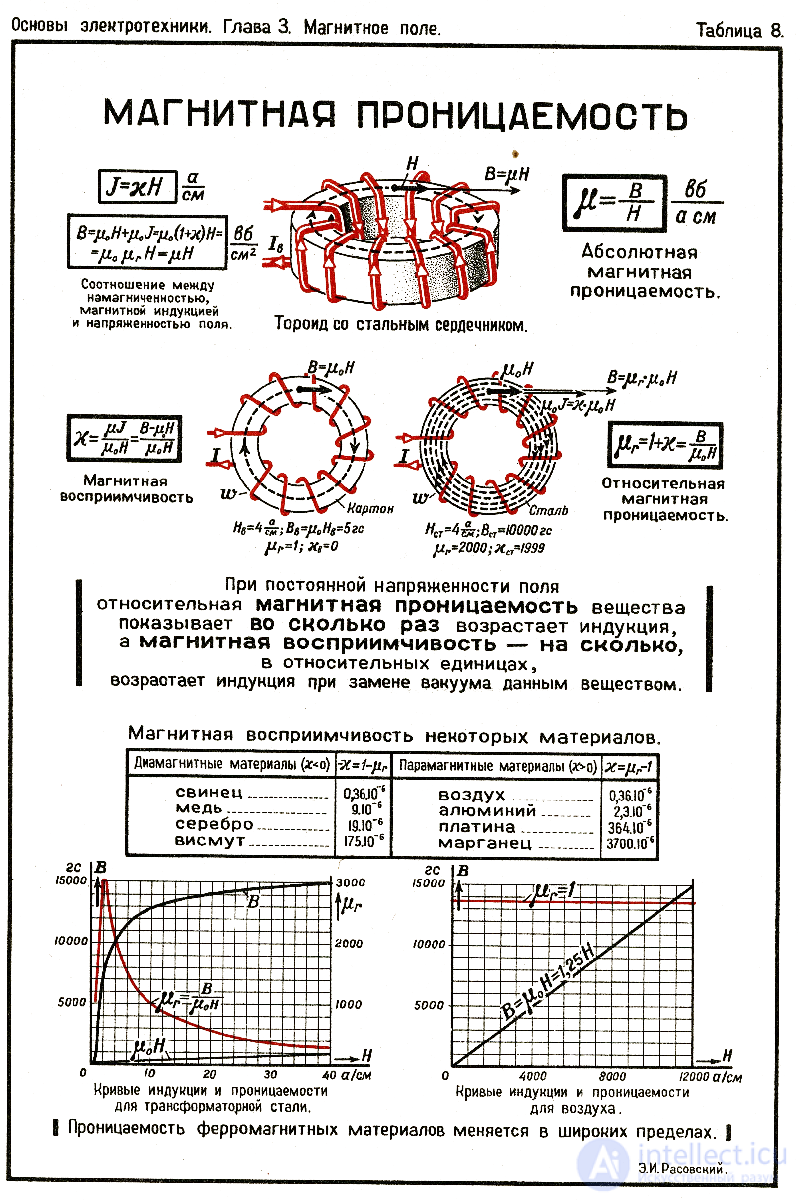
Магнитная проницаемость сильно зависит от величины поля для нелинейных по магнитной восприимчивости сред (типичный пример — ферромагнетики, для которых характерен магнитный гистерезис). Для таких сред магнитная проницаемость, как независящее от поля число, может указываться приближенно, в линейном приближении.
Для неферромагнитных сред линейное приближение μ=const достаточно хорошо выполняется для широкого диапазона изменения величины поля.
Все магнетики, в зависимости от характера влияния их собственного поля на суммарное магнитное поле, можно разделить на три группы:
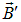 направлен в ту же сторону, что и вектор внешнего магнитного поля
направлен в ту же сторону, что и вектор внешнего магнитного поля 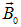 ;
;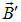 и
и 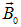 направлены в противоположные стороны;
направлены в противоположные стороны;В парамагнитных телах собственное поле 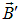 увеличивает магнитный поток и, следовательно, парамагнитные тела притягиваются к магниту. В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита.
увеличивает магнитный поток и, следовательно, парамагнитные тела притягиваются к магниту. В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита.

Как показывает опыт, вектор магнитной индукции собственного поля пара- и диамагнетика пропорционален вектору магнитной индукции внешнего поля B0
|
|
(7.2) |
Безразмерный коэффициент пропорциональности cm называется магнитной восприимчивостью вещества и является безразмерной величиной. У диамагнитных веществ магнитная восприимчивость является отрицательной величиной (cm < 0), у парамагнитных положительной (cm > 0). У ферромагнетиков магнитная восприимчивость cm зависит от величины магнитной индукции внешнего поля B0, поэтому в общем случае зависимость собственного поля ферромагнетика от внешнего нельзя считать линейной.
Результирующее магнитное поле в присутствии магнетика равно:
|
|
(7.3) |
Сравнивая (7.3) с (7.1), получим
|
|
(7.4) |
Отсюда находим связь собственного поля с внешним
|
|
(7.5) |
аналогичную соответствующим выражениям для диэлектриков.
Для объяснения намагничивания тел Ампер предположил, что в атомах и молекулах вещества циркулируют особые круговые токи —
молекулярные токи . Каждый такой ток создает в окружающем пространстве магнитное поле. В силу хаотической ориентации магнитных моментов отдельных молекулярных токов суммарный магнитный момент тела равен нулю. Под действием внешнего магнитного поля магнитные моменты молекулярных токов приобретают преимущественную ориентацию в одном направлении, вследствие чего вещество намагничивается — его суммарный магнитный момент становится отличным от нуля, возникает дополнительное поле  (рис. 7.1).
(рис. 7.1).
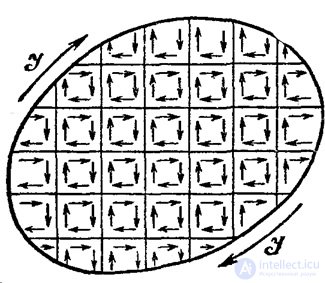
Рис. 7.1. Молекулярные токи в магнетике
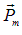 . Намагничение (Степень намагниченности) магнетика естественно охарактеризовать магнитным моментом единицы объема, называемого вектором намагничивания (или намагниченностъю).
. Намагничение (Степень намагниченности) магнетика естественно охарактеризовать магнитным моментом единицы объема, называемого вектором намагничивания (или намагниченностъю).
|
Вектор намагничивания (или Намагниченность)
|
Здесь dV — элементарный (физически бесконечно малый) объем магнетика, взятый в окрестности некоторой точки, 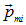 — магнитные моменты отдельных молекулярных токов. В формуле (7.6) суммируются магнитные моменты всех молекулярных токов, находящихся внутри объема dV.
— магнитные моменты отдельных молекулярных токов. В формуле (7.6) суммируются магнитные моменты всех молекулярных токов, находящихся внутри объема dV.
|
В СИ единицей измерения вектора намагничивания является ампер на метр (А/м):
|
Поляризуемость диэлектрика (плотность электрического дипольного момента) связывалась с возникновением поверхностных зарядов, которые изменяли электрическое поле в среде. Об этом говорит сайт https://intellect.icu . Аналогично этому, намагниченность магнетика приводит к возникновению поверхностных токов, что меняет магнитное поле. На рис. 7.2 показан образец магнетика, помещенный во внешнее магнитное поле 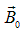 .
.
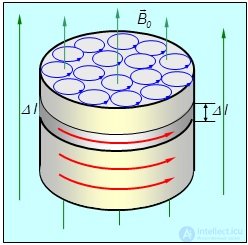
Рис. 7.2. Молекулярные токи в магнетике, помещенном в магнитном поле,
создают собственное поле, подобное полю соленоида с током I
Молекулярные токи, показанные на торце образца, ориентированы так, что их магнитные моменты выстроились параллельно вектору 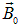 . Видно, что токи в толще магнетика компенсируют друг друга. Нескомпенсированными оказываются только токи вблизи поверхности образца. Складываясь, они приводят к поверхностным токам (показаны красными стрелками на рис. 7.2 и черными стрелками на рис. 7.3).
. Видно, что токи в толще магнетика компенсируют друг друга. Нескомпенсированными оказываются только токи вблизи поверхности образца. Складываясь, они приводят к поверхностным токам (показаны красными стрелками на рис. 7.2 и черными стрелками на рис. 7.3).
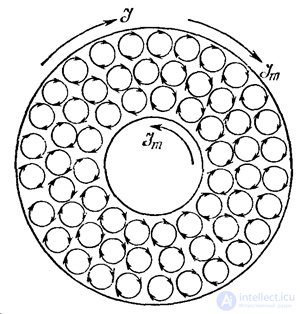
Рис. 7.3. Образование молекулярных токов на поверхностях магнетика
Такая система эквивалентна соленоиду. В формуле для магнитной индукции поля соленоида
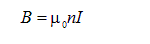
величина n есть число витков на единицу длины
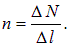
С другой стороны, произведение 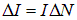 сть полный ток через элемент длиной Δl. Поэтому формула для соленоида применима к нашему магнетику, если заменить произведение nI на линейную плотность поверхностного тока ΔI/Δl. Получаем тогда следующее выражение для величины магнитной индукции поля В ', создаваемого молекулярными токами
сть полный ток через элемент длиной Δl. Поэтому формула для соленоида применима к нашему магнетику, если заменить произведение nI на линейную плотность поверхностного тока ΔI/Δl. Получаем тогда следующее выражение для величины магнитной индукции поля В ', создаваемого молекулярными токами
|
|
(7.7) |
С другой стороны, магнитный момент элемента поверхностного тока, текущего по участку соленоида длиной Δl, равен
|
|
(7.8) |
где S — поперечное сечение образца. По определению вектора намагничивания
|
|
(7.9) |
Сравнивая (7.7) и (7.9), находим связь вектора намагниченности с полем, создаваемым молекулярными токами
|
|
(7.10) |
С учетом (7.1) и (7.5) можем записать
|
|
(7.11) |
В диэлектриках, помимо силовой характеристики электрического поля Е, мы ввели также вспомогательную величину — вектор электрического смещения
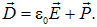
В наиболее распространенном случае линейной зависимости поляризованности изотропного диэлектрика от напряженности поляризующего поля имело место соотношение
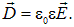
Для магнетиков аналогичным образом также вводится вспомогательная величина — напряженность магнитного поля Н
|
|
(7.12) |
обратите внимание на разные знаки, с которыми входят Р для диэлектриков и вектор J для магнетиков). С учетом полученных выше соотношений имеем
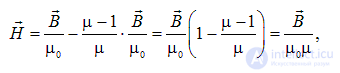
так что
|
|
(7.13) |
|
В СИ единицей измерения напряженности магнитного поля является ампер на метр (А/м):
|
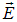 является именно вектор магнитной индукции
является именно вектор магнитной индукции 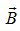 , а векторы
, а векторы 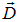 и
и 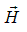 играют вспомогательную роль. Следует избегать ложных иллюзий, вызванных исторически закрепившимся названием «напряженность» магнитного поля для вектора
играют вспомогательную роль. Следует избегать ложных иллюзий, вызванных исторически закрепившимся названием «напряженность» магнитного поля для вектора 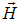 . В терминах
. В терминах 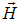 полученные соотношения принимают вид
полученные соотношения принимают вид
|
|
(7.14) |
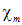 — магнитная восприимчивость магнетика.
— магнитная восприимчивость магнетика.
Мы видели, что циркуляция магнитной индукции в вакууме определялась током, пронизывающим выбранный контур L
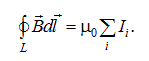
Аналогичное выражение, естественно, справедливо и для циркуляции вектора 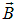 в веществе, но циркуляция собственного поля магнетика
в веществе, но циркуляция собственного поля магнетика
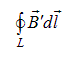
приведет к появлению в правой части суммы молекулярных токов, которые нам не известны. Это крайне неудобно. Положение спасает введенный вектор напряженности магнитного поля Н. Из определения (7.12) и соотношения (7.10) следует
|
|
(7.15) |
так что циркуляция вектора напряженности магнитного поля определяется только макроскопическими токами в системе
|
|
(7.16) |
где I — полный макроскопический ток через контур L. Его можно выразить через плотность тока 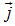 через любую поверхность S, натянутую на контур L
через любую поверхность S, натянутую на контур L
|
|
(7.17) |
где dS = ndS, а вектор 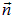 — единичный нормальный вектор к элементарной площадке площадью dS.
— единичный нормальный вектор к элементарной площадке площадью dS.
Для иллюстрации применения полученных формул вычислим магнитную индукцию в соленоиде с линейной плотностью витков n и силой тока I, если витки намотаны на сердечник с магнитной проницаемостью m. Найдем циркуляцию вектора напряженности магнитного поля Н по тому же контуру, что и прежде (см. рис. 6.18). Ответ нам, в сущности, известен
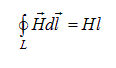
(ср. с (6.34)). Контур охватывает тот же суммарный ток nlI, и (7.16) приводит к равенству
H=nl
Используя теперь связь В = m0mH, получаем выражение для магнитной индукции поля соленоида, заполненного магнетиком
|
|
(7.18) |
По сравнению с выражением (6.35) для соленоида без сердечника, здесь появился дополнительный множитель μ.
|
|
(7.19) |
Поскольку произведение длины окружности 2πr на частоту вращения n есть линейная скорость движения электрона на орбите
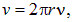
то
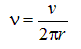
и
|
|
(7.20) |
Эта величина называется орбитальным магнитным моментом электрона. Направление вектора 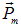 образует с направлением тока (то есть с направлением движения положительных зарядов) правовинтовую систему. Движущийся по орбите электрон обладает моментом импульса
образует с направлением тока (то есть с направлением движения положительных зарядов) правовинтовую систему. Движущийся по орбите электрон обладает моментом импульса
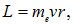
где mе — масса электрона. Вектор L называют орбитальным моментом импульса электрона. Он также образует с направлением движения электрона правовинтовую систему. Следовательно, для отрицательно заряженногого электрона направления векторов 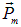 и
и 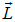 противоположны.
противоположны.
Отношение магнитного момента элементарной частицы к ее моменту импульса называется гиромагнитным (магнитомеханическим) отношением. Для электрона оно равно
|
|
(7.21) |
Кроме орбитального момента импульса электрон обладает собственным моментом импульса 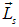 и соответствующим собственным магнитным моментом
и соответствующим собственным магнитным моментом 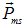 , для которых гиромагнитное (магнитомеханическое) отношение в два раза больше
, для которых гиромагнитное (магнитомеханическое) отношение в два раза больше
|
|
(7.22) |
Собственный механический момент (спин) и связанный с ним собственный (спиновый) магнитный момент являются неотъемлемыми свойствами электрона, как его масса и заряд. Аналогичная картина имеет место и для других элементарных частиц. Природа спина будет обсуждена при изучении основ квантовой механики. Отметим только, что в очень грубом приближении его можно связать с вращением частицы вокруг собственной оси (от англ. spin — верчение).
Спин элементарных частиц пропорционален фундаментальной постоянной — так называемой постоянной Планка
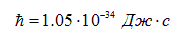
и выражается через нее следующим образом
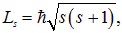
где 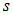 — так называемое «спиновое квантовое число», принимающее значения
— так называемое «спиновое квантовое число», принимающее значения
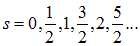 .
.
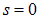 , у фотона
, у фотона 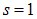 , у предполагаемого кванта гравитационного поля «гравитона» это квантовое число должно быть равно
, у предполагаемого кванта гравитационного поля «гравитона» это квантовое число должно быть равно 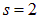 . Квантовое число, определяющее спин, как и сам спин, является одной из характеристик элементарных частиц наряду с массой и зарядом.
. Квантовое число, определяющее спин, как и сам спин, является одной из характеристик элементарных частиц наряду с массой и зарядом.
Таким образом, собственный момент импульса — спин — электронов, протонов и нейтронов равен
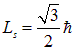
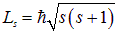 общепринято говорить «спин», а называть соответствующее ему квантовое число, к недоразумениям это не приводит, то есть общепринято говорить, что спин электрона равен половине или 1/2. Согласно (7.22), собственный магнитный момент электрона равен
общепринято говорить «спин», а называть соответствующее ему квантовое число, к недоразумениям это не приводит, то есть общепринято говорить, что спин электрона равен половине или 1/2. Согласно (7.22), собственный магнитный момент электрона равен
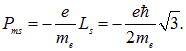
Величину
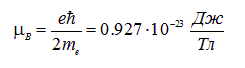
называют магнетоном Бора.
Как показывается в квантовой механике, орбитальный момент импульса выражается через соответствующее ему квантовое число так же, как и собственный момент импульса (спин)
|
|
(7.23) |
Важно то, что орбитальное квантовое число 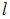 может принимать только целочисленные значения.
может принимать только целочисленные значения.
Как видно из (7.21) и (7.23), наименьший отличный от нуля орбитальный магнитный момент равен магнетону Бора:
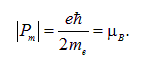
Результирующий магнитный момент атома образуется в результате векторного сложения (по правилам квантовой механики!) магнитных моментов всех элементарных частиц, содержащихся в атоме. Картина еще более усложняется при рассмотрении совокупностей молекул и атомов.
В диамагнитных материалах, помещенных во внешнее магнитное поле B0, возникает внутреннее поле, направленное навстречу намагничивающему полю.
Это связано с тем, что суммарный магнитный момент диамагнитного атома равен нулю. Когда диамагнитное вещество помещают во внешнее магнитное поле, то под действием этого поля возникает прецессия электронных орбит.
Поскольку электрон в атоме можно уподобить круговому току, характеризуемому магнитным моментом Рm , во внешнем магнитном поле на магнитный момент 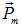 этого кругового тока начинает действовать вращательный момент
этого кругового тока начинает действовать вращательный момент
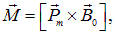
под действием этого момента М вектор орбитального момента электрона Рm начнет прецессировать вокруг направления вектора магнитной индукции B0, то есть получит дополнительное равномерное вращение, при котором вектор Рm будет описывать конус вокруг направления B0 (рис. 7.4).
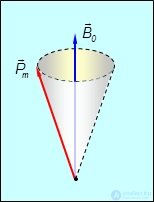
Рис. 7.4. Прецессия орбитального магнитного момента Рm электрона
вокруг вектора магнитной индукции B0 внешнего поля
Таким образом, вектор Рm , перпендикулярный к плоскости электронной орбиты, сохраняет неизменный угол a наклона к внешнему полю и вращается вокруг B0 с некоторой угловой скоростью. Это движение сродни прецессии оси волчка в поле сил тяжести.
Частота этой прецессии
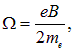
называемая ларморовой частотой, не зависит ни от угла наклона орбиты электрона к вектору B0, ни от радиуса орбиты или скорости электрона и, следовательно, для всех электронов одинакова. Прецессия электронной орбиты создает дополнительное движение электрона во внешнем магнитном поле B0. Это движение, как и любое движение зарядов, приводит к возникновению индуцированного магнитного момента, причем в данном случае направленного против поля (рис. 7.5).
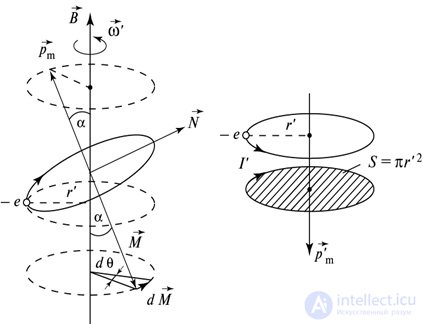
Рис. 7.5. Формирование индуцированного магнитного момента, направленного против внешнего магнитного поля
Следовательно,
|
В диамагнитных веществах во внешнем магнитном поле B0 возникает направленное противоположно B0 индуцированное магнитное поле В', которое ослабляет внешнее поле
то есть для диамагнетиков
|
Молекулы парамагнитного вещества имеют собственное магнитное поле, обусловленное тем, что у парамагнетиков векторная сумма орбитальных и спиновых моментов электронов не равна нулю. В отсутствие внешнего магнитного поля эти магнитные микрополя молекул тепловым движением ориентированы в пространстве хаотически, и поэтому суммарное магнитное макрополе парамагнетика равно нулю. При помещении парамагнитного вещества во внешнее магнитное поле B0 магнитные моменты атомов приобретают преимущественную ориентацию вдоль поля B0, которая тем больше, чем больше B0, причем эффект с увеличением температуры уменьшается. В результате суммарное собственное магнитное поле парамагнетика В становится отличным от нуля и направлено вдоль внешнего поля B0.
Следовательно,
|
Парамагнетик, помещенный во внешнее магнитное поле, усиливает это поле
то есть для парамагнетиков
|
Следует отметить, что диамагнитный эффект имеет место для всех веществ без исключения, в том числе и для парамагнетика, однако величина диамагнитного эффекта существенно меньше парамагнитного, и в этом случае его можно не учитывать.
Если диамагнитный эффект не зависит от температуры вещества, то парамагнитный зависит, поскольку тепловое движение атомов и молекул нарушает преимущественную ориентацию по полю их магнитных моментов во внешнем магнитном поле (рис. 7.6).
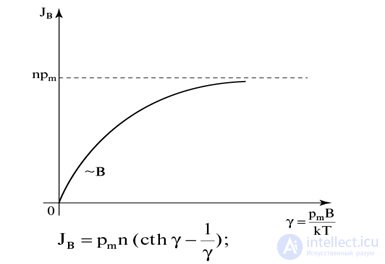
Рис. 7.6. Зависимость намагниченности парамагнетика от обратной температуры
Зависимость магнитной восприимчивости 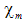 парамагнетиков от температуры была установлена Кюри и выражается формулой
парамагнетиков от температуры была установлена Кюри и выражается формулой
|
|
(7.24) |
Диамагнетики выталкиваются из магнитного поля, в то время как парамагнетики втягиваются в магнитное поле. Поэтому тонкие стержни из пара- и диамагнетиков, подвешенные на нитях и помещенные между полюсами магнита, ведут себя по-разному. Магнитное поле разворачивает диамагнитный стержень таким образом, что он поворачивается перпендикулярно силовым линиям, а парамагнитный стержень — встает параллельно силовым линиям (см. рис. 7.7).
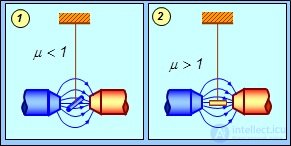
Рис. 7.7. Поведение пара- и диамагнетиков во внешнем магнитном поле:
1 — парамагнитный стержень; 2 — диамагнитный стержень
На рис. 7.8 показан опыт, в котором палочка из висмута, являющегося диамагнетиком, подвешивается в поле сильного электромагнита. При включении поля палочка разворачивается и устанавливается параллельно поверхности полюсов магнита, то есть перпендикулярно полю.

Рис. 7.8. Диамагнетики в магнитном поле
На рис. 7.9. представлен опыт, в котором демонстрируется ориентация длинного металлического парамагнитного образца и длинной ампулы с раствором парамагнитной соли вдоль магнитного поля, создаваемого магнитом.

Рис 7.9. Парамагнетики в магнитном поле
У ферромагнетиков, так же как и у парамагнитных материалов, собственное поле при намагничивании усиливает внешнее поле, то есть cm > 0 и достигает очень больших значений (для железа, например, cm = 5 000, но есть сплавы с еще большими значениями cm = 50 000).
Ферромагнитные вещества обладают рядом отличительных свойств:
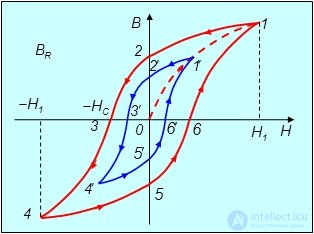
Рис. 7.10. Зависимость магнитной индукции В от напряженности магнитного поля Н
(основная кривая намагничивания 01, а также частная 1'2'3'4'5'6' и предельная 123456 петли гистерезиса)
Изучение строения ферромагнетиков показало, что ферромагнетик состоит из множества самопроизвольно (спонтанно) намагниченных областей, с линейными размерами порядка 10–3–10–4 см, которые называются доменами. Причиной их образования является сильное взаимодействие спиновых магнитных моментов, которые, стремясь стать параллельными, ориентируются одинаково в пределах достаточно большой области, которая и становится доменом. Раз в каждом из доменов магнитные моменты всех его молекул или атомов направлены в одну сторону, то их векторная сумма дает отличный от нуля магнитный момент всего домена.
Если ферромагнетик не намагничен (J = 0), то магнитные моменты отдельных доменов распределены по направлениям изотропно, и суммарный момент ферромагнетика равен нулю. При включении внешнего магнитного поля происходит рост доменов, ориентированных вдоль внешнего поля, за счет доменов, магнитные поля которых имеют иное направление. С увеличением внешнего поля происходит рост собственного магнитного поля ферромагнетика. В слабых полях такой рост носит обратимый характер. В более сильных полях одновременно происходит переориентация магнитных моментов в пределах всего домена. Этот процесс является необратимым, чем объясняется гистерезис и остаточная намагниченность. В очень сильном внешнем поле все домены имеют одинаковую ориентацию вдоль внешнего поля. Наступает состояние магнитного насыщения ферромагнетика.
Качественная картина роста доменов, ориентированных параллельно внешнему полю, при увеличении внешнего поля в процессе намагничивания ферромагнетика показана на рис. 7.11.
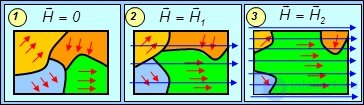
Рис. 7.11. Намагничивание ферромагнетика во внешнем поле:
1 — Н = 0; 2 — Н = Н1; 3 — Н = Н2, Н2 > Н1
В сильных полях с (напряженность H порядка 200 А/м и более) намагничивание достигает насыщения (рис. 7.12).
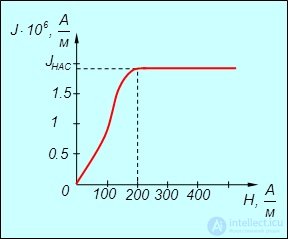
Рис. 7.12. Насыщение намагничивания в сильных внешних полях
При достижении насыщения магнитная индукция поля В продолжает расти вместе с внешним полем по линейному закону
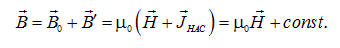
В состоянии насыщения практически все домены выстроены вдоль внешнего поля Н. Поэтому индукция В' перестает расти и на увеличение B не влияет, но B0 с ростом H продолжает увеличиваться. Поэтому в состоянии насыщения магнитная индукция внутри ферромагнетика продолжает медленно линейно возрастать.
При изменении напряженности H внешнего поля зависимость В = В(H) имеет вид, изображенный на рисунке 7.10. В начальный момент времени, если ферромагнетик не был намагничен, то H = 0 и В = 0, затем при увеличении H до значения H1 индукция возрастает по кривой 01 до значения В1. При плавном уменьшении напряженности внешнего магнитного поля индукция В будет изменяться по кривой 12, а не по первоначальной кривой 01. В результате, когда напряженность внешнего поля станет равной нулю, намагничивание образца не исчезает и характеризуется величиной Br, которая называется остаточной индукцией. Намагниченность имеет при этом значение Jr, называемое остаточной намагниченностью. В этом проявляется необратимость процесса намагничивания ферромагнетика.
Как уже говорилось, домены — достаточно крупные образования, и тепловое движение не в состоянии разрушить остаточную индукцию. Для этого надо приложить обратное внешнее поле. Магнитная индукция становится равной нулю (точка 3 на рис. 7.10) под действием противоположного по направлению поля величиной Hс. Напряженность размагничивающего поля Hс называется коэрцитивной силой.
При действии на ферромагнетик переменного магнитного поля с напряженностью Н < H1 индукция результирующего поля изменяется в соответствии с кривой 1'2'3'4'5'6'1', называемой частной петлей гистерезиса. Если амплитуда напряженности переменного магнитного поля Н > H1, то получаем предельную петлю гистерезиса 1234561, соответствующую насыщению намагниченности.
На рис. 7.13 показан опыт, в котором наблюдается петля гистерезиса. Демонстрируется электронно-лучевая трубка с катушками вертикального и горизонтального отклонения луча. При подаче одинакового переменного напряжения на обе пары катушек на экране видна наклонная прямая линия. Затем в горизонтальные катушки, отклоняющие луч по вертикали, вставляются ферромагнитные стержни, и вертикальное отклонение луча становится пропорциональным индукции магнитного поля в ферромагнетике. При этом на экране осциллографа наблюдается петля гистерезиса для данного ферромагнетика.
Рис. 7.13. Петля гистерезиса
Поскольку магнитная индукция В в ферромагнетике неоднозначно зависит от напряженности поля Н, то указываемая в справочниках магнитная проницаемость ферромагнетиков
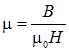 ,
,
общепринято определять только для основной кривой намагничивания.
При высоких температурах вещество ферромагнетика превращается в парамагнетик, поскольку доменная структура вещества разрушается под действием теплового движения. Превращение происходит при вполне определенной для каждого ферромагнетика температуре ТС, называемой точкой Кюри; для железа ТС = 1 043 К, для кобальта ТС = 1 393 К и для никеля ТС = 631 К.
На рис. 7.14 демонстрируется исчезновение притяжения ферромагнитной пластинки к постоянному магниту при нагревании ее выше точки Кюри. Пластинка подвешена на тонкой проволоке в стороне от магнита так, что натянутая за счет притяжения к магниту проволока наклонена относительно вертикали. Под пластинку помещают газовую горелку, и после нагрева выше температуры Кюри пластинка перестает натягивать проволоку к магниту, отходит от него, и подвес принимает вертикальное положение.

Рис. 7.14. Разрушение ферромагнитных свойств ферромагнетика при нагревании выше точки Кюри
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика