Лекция
Привет, Вы узнаете о том , что такое интерференция света, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое интерференция света , настоятельно рекомендую прочитать все из категории Колебания и волны (Оптика, акустика и радиофизика).
|
Интерференция волн — это явление усиления или ослабления колебаний в разных точках пространства (пространственное перераспределение энергии), наблюдаемое при наложении двух или нескольких волн. |
Интерференция возможна для волн любой природы. Ниже будут наиболее подробно исследованы проявления интерференции электромагнитных (световых) волн. интерференция света характеризуется регулярным чередованием в пространстве областей повышенной и пониженной интенсивности света, которые возникают в результате наложения так называемых когерентных световых пучков.
Для электромагнитного поля справедлив принцип суперпозиции. Так как свет имеет электромагнитную природу, то применение принципа суперпозиции означает, что результирующая напряженность электрического (магнитного) поля двух световых волн, проходящих через одну точку, равна векторной сумме напряженностей электрического (магнитного) поля каждой из волн в отдельности.
Как известно, интенсивность электромагнитной волны пропорциональна среднему по времени значению квадрата амплитуды колебаний вектора напряженности электромагнитного поля:
|
|
|
(4.1) |
Поэтому интенсивность волны, как и любая другая нелинейная по полю (в данном случае — квадратичная по полю) величина принципу суперпозиции не подчиняется. Для нелинейных по полю величин принципа суперпозиции нет. Если векторы напряженности поля складываются, то интенсивности волн и общем случае не складываются. Отвлекаясь от деталей можно утверждать, что именно в этом и состоит причина такого явления как интерференция волн.
Рассмотрим две электромагнитные волны одинаковой частоты, которые накладываются друг на друга и возбуждают в некоторой точке пространства два колебания одинакового направления:
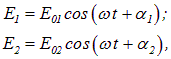
где 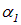 и
и 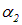 не зависящие от времени начальные фазы колебаний в рассматриваемой точке
не зависящие от времени начальные фазы колебаний в рассматриваемой точке
Амплитуду результирующего колебания в данной точке можно найти с помощью векторной диаграммы.
Эта амплитуда Е0 зависит от разности фаз складываемых колебаний в данной точке. В рассматриваемом случае равенства частот волн разность фаз колебаний не изменяется во времени и равна 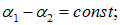 при этом результирующая амплитуда Е0 также остается постоянной во времени:
при этом результирующая амплитуда Е0 также остается постоянной во времени:
|
|
|
(4.2) |
|
Когерентные волны — это волны, которые возбуждают колебания в точках пространства, разность фаз которых остается неизменной во времени. |
Когерентность — это согласованное протекание нескольких колебательных или волновых процессов.
Для когерентных волн косинус разности фаз имеет постоянное во времени значение (но свое для каждой точки пространства), так что результирующая интенсивность света, как следует из (4.1) и (4.2), равна
|
|
|
(4.3) |
Последнее слагаемое в полученном выражении носит название интерференционного члена. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности. Если интенсивности обеих интерферирующих волн одинаковы (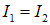 ), то в максимумах
), то в максимумах 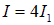 , а в минимумах
, а в минимумах 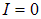 .
.
Если накладываются некогерентные волны, то в данной точке пространства складываются колебания, разность фаз которых не постоянна во времени и, вообще говоря, принимает случайные значения. Если при этом случайно меняющаяся разность фаз — за некоторое время 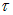 — принимает все возможные значения в интервале длиной
— принимает все возможные значения в интервале длиной 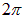 , то среднее (за время
, то среднее (за время 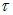 ) значение косинуса в интерференционном члене равно нулю и наблюдаемая интенсивность света во всех точках пространства представляется просто суммой интенсивностей двух волн:
) значение косинуса в интерференционном члене равно нулю и наблюдаемая интенсивность света во всех точках пространства представляется просто суммой интенсивностей двух волн:
|
|
|
(4.4) |
При равенстве интенсивностей приходящих волн получаем 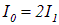 . Когда мы включаем две одинаковые лампочки, и помещение освещается в два раза ярче, чем одной из них, то это означает отсутствие интерференции и проявление соотношения (4.4). Таким образом,
. Когда мы включаем две одинаковые лампочки, и помещение освещается в два раза ярче, чем одной из них, то это означает отсутствие интерференции и проявление соотношения (4.4). Таким образом,
|
необходимым условием наблюдения интерференции волн является их когерентность. |
Монохроматическая плоская электромагнитная волна описывается следующим выражением для напряженности поля в любой точке пространства, определяемой радиус-вектором r:
|
|
|
(4.5) |
где Е0, 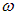 ,
, 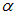 и
и  являются постоянными величинами. Однако всякая реальная световая волна образуется наложением колебаний различных частот, заключенных в конечном интервале
являются постоянными величинами. Однако всякая реальная световая волна образуется наложением колебаний различных частот, заключенных в конечном интервале 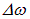 . Согласно формуле
. Согласно формуле 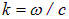 разбросу частот
разбросу частот 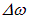 соответствует разброс значений волнового числа
соответствует разброс значений волнового числа 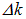 . Следует отметить, что разброс волнового вектора
. Следует отметить, что разброс волнового вектора 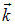 может быть связан также с разбросом направлений распространения волн, который характеризуется векторной величиной
может быть связан также с разбросом направлений распространения волн, который характеризуется векторной величиной  .
.
Сначала обсудим временную когерентность, которая связана с разбросом частот 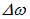 . Рассмотрим случай наложения в некоторой точке пространства двух световых колебаний с несколько различающимися частотами
. Рассмотрим случай наложения в некоторой точке пространства двух световых колебаний с несколько различающимися частотами 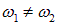 :
:
|
|
|
(4.6) |
Интерференционный член

при сделанных предположениях будет зависеть от времени и разности частот
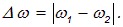
Всякий оптический прибор, с помощью которого наблюдается интерференция света (фотопленка, человеческий глаз и др.), обладает определенной инертностью, которая характеризуется временем 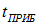 регистрации прибором интерференционной картины. При этом оптический прибор регистрирует картину, усредненную по промежутку времени
регистрации прибором интерференционной картины. При этом оптический прибор регистрирует картину, усредненную по промежутку времени 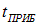 . Если за это время косинус в интерференционном члене
. Если за это время косинус в интерференционном члене
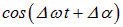
с равной вероятностью принимает все значения от –1 до +1, то среднее значение интерференционного члена будет равно нулю. Интерференционная картина не будет видна, то есть регистрируемая прибором интенсивность окажется равной сумме интенсивностей, создаваемых в данной точке каждой волной в отдельности. Если же за время 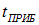 значение косинуса остается практически неизменным, то прибор зарегистрирует интерференцию. Таким образом, для характеристики когерентных свойств световых волн вводится время когерентности
значение косинуса остается практически неизменным, то прибор зарегистрирует интерференцию. Таким образом, для характеристики когерентных свойств световых волн вводится время когерентности 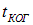 , которое определяется как время, за которое изменение разности фаз волн, накладывающихся в данной точке пространства, достигает значения
, которое определяется как время, за которое изменение разности фаз волн, накладывающихся в данной точке пространства, достигает значения 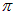 :
:
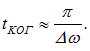
При

прибор не зафиксирует интерференцию, а при

прибор обнаружит интерференционную картину. За время когерентности 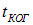 волна распространяется на расстояние
волна распространяется на расстояние

называемое длиной когерентности.
Для наблюдения интерференционной картины обычно используют пучки света от одного источника, но прошедшие разные расстояния до точки наблюдения. Это означает, что интерферируют волны, испущенные источником в разное время. Если частота источника «плавает», то при разности хода волн до точки наблюдения 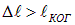 разница во времени испускания волн будет
разница во времени испускания волн будет 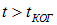 , что означает невозможность наблюдения интерференции.
, что означает невозможность наблюдения интерференции.
В качестве примера укажем типичные значения длины когерентности для естественного оптического источника с узкополосным светофильтром с шириной полосы пропускания  вблизи середины видимого диапазона (
вблизи середины видимого диапазона (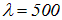 нм) и для газового лазера — источника оптического излучения с высокой временной когерентностью, для которого ширина полосы на два-три порядка меньше. В первом случае оценка длины когерентности дает значение
нм) и для газового лазера — источника оптического излучения с высокой временной когерентностью, для которого ширина полосы на два-три порядка меньше. В первом случае оценка длины когерентности дает значение
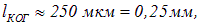
а во втором случае — для лазера —
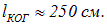
Таким образом, наблюдение интерференционной картины от обычных оптических источников возможно лишь при малых разностях хода волн, например, при интерференции в тонких пленках, в то время как использование лазерного излучения существенно упрощает эту задачу.
В идеализированном случае при наложении монохроматических воли со строго фиксированными и равными частотами (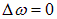 ) время и длина когерентности становятся бесконечно большими, поэтому, естественно, в таких условиях интерференционная картина наблюдалась бы при любых разностях хода.
) время и длина когерентности становятся бесконечно большими, поэтому, естественно, в таких условиях интерференционная картина наблюдалась бы при любых разностях хода.
Изменение разности фаз колебаний может происходить не только из-за разбросa частот 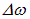 , но и вследствие разброса волновых векторов
, но и вследствие разброса волновых векторов 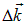 . Поэтому наряду с временной когерентностью, определяемой временем когерентности, вводится понятие пространственной когерентности. Возникновение в некоторой точке пространства колебаний, возбуждаемых волнами с целым набором различных по направлению векторов
. Поэтому наряду с временной когерентностью, определяемой временем когерентности, вводится понятие пространственной когерентности. Возникновение в некоторой точке пространства колебаний, возбуждаемых волнами с целым набором различных по направлению векторов 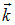 , имеет место, если эти волны испускаются различными участками протяженного источника света.
, имеет место, если эти волны испускаются различными участками протяженного источника света.
Рассмотрим для определенности светящийся диск АВ, который из точки М виден под углом  (рис. 4.1)
(рис. 4.1)
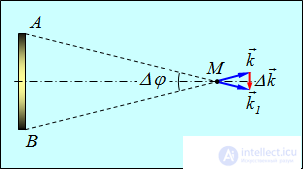
Рис. 4.1. Пространственная когерентность света от протяженного источника:
угол 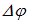 характеризует разброс волновых векторов Ак
характеризует разброс волновых векторов Ак
Угол 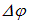 характеризует разброс волновых векторов
характеризует разброс волновых векторов 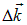 . Об этом говорит сайт https://intellect.icu . Таким образом, в фазу электромагнитной волны
. Об этом говорит сайт https://intellect.icu . Таким образом, в фазу электромагнитной волны
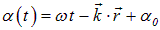
надо подставить выражения:
|
|
|
(4.7) |
Тогда
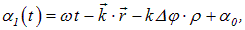
так что
|
|
|
(4.8) |
где 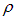 — проекция радиус-вектора r на направление вектора
— проекция радиус-вектора r на направление вектора 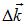 . В формулах (4.7) и ниже предполагается, что
. В формулах (4.7) и ниже предполагается, что 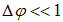 . Вектор
. Вектор 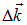 , как видно из рисунка, можно считать параллельным протяженному источнику, и, соответственно, фронту волны.
, как видно из рисунка, можно считать параллельным протяженному источнику, и, соответственно, фронту волны.
Следовательно, фаза колебаний при переходе от одной точки волновой поверхности к другой изменяется. Введем расстояние 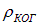 , при смещении на которое вдоль волновой поверхности изменение фазы достигает значения
, при смещении на которое вдоль волновой поверхности изменение фазы достигает значения 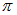 :
:

откуда
|
|
|
(4.9) |
Расстояние  характеризует пространственную когерентность волны и называется радиусом когерентности.
характеризует пространственную когерентность волны и называется радиусом когерентности.
Пусть длина 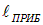 характеризует пространственное разрешение фотопленки или человеческого глаза. Интерференционный член усредняется по части пространства с линейными размерами порядка
характеризует пространственное разрешение фотопленки или человеческого глаза. Интерференционный член усредняется по части пространства с линейными размерами порядка 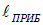 . При
. При
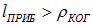
среднее значение косинуса равно нулю, что не позволяет наблюдать интерференцию. В противоположном случае, когда
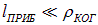
наблюдается четкая интерференционная картина.
Приведем пример. Угловой размер Солнца
 ,
,
примерно в середине видимого диапазона длина волны видимого света
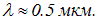
Следовательно, радиус когерентности приходящих от Солнца световых волн примерно равен

При таком малом радиусе когерентности невозможно непосредственно наблюдать интерференцию солнечных лучей, поскольку разрешающая способность человеческого глаза составляет лишь 0.1 мм. Однако в 1807 г. Т. Юнг провел первое наблюдение интерференции именно с солнечным светом. Для этого он пропускал солнечные лучи в темную комнату через маленькое отверстие, сделанное тонкой иглой. Отверстие на несколько порядков уменьшало угловой размер  источника света и, соответственно, увеличивало радиус когерентности.
источника света и, соответственно, увеличивало радиус когерентности.
Механизм излучения электромагнитных волн заключается в том, что атом, находящийся в возбужденном состоянии, при переходе на более низкий энергетический уровень излучает электромагнитную волну. Процесс излучения длится около  с. Таким образом, атом излучает волну, представляющую собой часть синусоиды (см. рис. 4.2), которая называется волновым цугом.
с. Таким образом, атом излучает волну, представляющую собой часть синусоиды (см. рис. 4.2), которая называется волновым цугом.
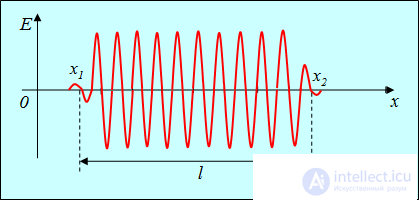
Рис. 4.2. Волновой цуг
Длина волнового цуга в вакууме равна

Естественный свет представляется совокупностью несогласованных между собой цугов волн, испускаемых отдельными атомами. Поэтому невозможно получить интерференцию от двух разных источников естественного света. Для получения когерентных световых волн тем или иным способом разделяют на две части волну, излучаемую одним источником. После прохождения различных оптических путей эти две части одной волны накладываются друг на друга (рис. 4.3).
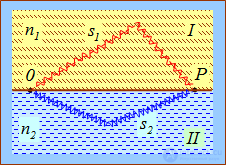
Рис. 4.3. Разделение волны от естественного источника
Предположим, что разделение на две когерентные волны происходит в некоторой точке 0, лежащей на границе раздела двух сред I и II. До точки Р в которой наблюдается интерференционная картина, одна волна проходит путь s1 в среде с показателем преломления п1, а вторая волна — путь s2 в среде с показателем преломления п2. Если начальные фазы обеих волн равны нулю, то в точке Р волны возбудят колебания
|
|
|
(4.10) |
где
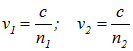
— фазовые скорости первой и второй волн соответственно. Разность фаз колебаний в точке Р равна
|
|
|
(4.11) |
Выражая циклическую частоту через длину волны l в вакууме
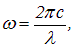
находим
|
|
|
(4.12) |
|
Оптическая разность хода — это разность
оптических длин путей, проходимых волнами. |
Запишем интенсивность результирующей волны в точке Р в виде
|
|
|
(4.13) |
Когда оптическая разность хода равна целому числу длин волн в вакууме (или, что то же самое, четному числу полуволн), то есть
|
|
|
(4.14) |
колебания в точке Р находятся в одинаковой фазе,  и наблюдается интерференционный максимум.
и наблюдается интерференционный максимум.
Если оптическая разность хода равна нечетному числу полуволн, то есть
|
|
|
(4.15) |
то колебания, возбуждаемые в точке Р обеими волнами, находятся в противофазе,  и наблюдается интерференционный минимум.
и наблюдается интерференционный минимум.
Установив общие закономерности, обратимся к конкретному примеру интерференции, когда источниками света служат две узкие параллельные щели, расположенные достаточно близко друг к другу. Пусть эти щели S1, и S2 находятся на расстоянии d друг от друга (рис. 4.4).
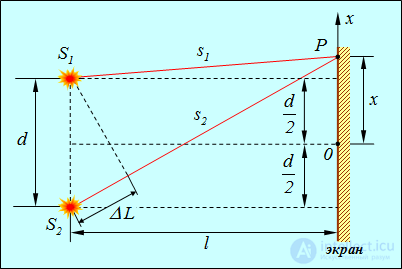
Рис. 4.4. Интерференция от двух когерентных источников света
Интерференция наблюдается в некоторой точке Р экрана, расположенного на расстоянии l от источников света (l>>d, 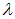 ). Начало отсчета на оси 0х выбрано в точке 0, симметричной относительно щелей.
). Начало отсчета на оси 0х выбрано в точке 0, симметричной относительно щелей.
Интенсивность в точке Р, расположенной на расстоянии x от начала отсчета, определяется оптической разностью хода, которая в данном случае (п = 1) равна геометрической разности хода
|
|
|
(4.16) |
Видно, что
|
|
|
(4.17) |
откуда
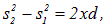
или
|
|
|
(4.18) |
Учитывая, что при l>>d
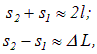
получаем
|
|
|
(4.19) |
Используя условия (4.14) и (4.15) для максимумов и минимумов интерференции, приходим к выводу, что в точках с координатами
|
|
|
(4.20) |
будут наблюдаться максимумы, а в точках
|
|
|
(4.21) |
— интерференционные минимумы.
|
Ширина интерференционной полосы — это расстояние между соседними минимумами интенсивности. |
С учетом (4.20) ширина интерференционной полосы равна
|
|
|
(4.22) |
причем 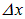 не зависит от порядка интерференции (величины т) и является постоянной величиной при заданных l, d,
не зависит от порядка интерференции (величины т) и является постоянной величиной при заданных l, d, 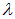
Для получения интерференционной картины необходимы когерентные световые пучки, для формирования которых применяются различные искусственные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали, как отмечалось выше, разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов со щелями, зеркал и преломляющих тел (призм). Обсудим некоторые из таких способов.
Метод Юнга
Источником света служит ярко освещенная щель S, от которой свет падает на две равноудаленные щели s1, и s2, параллельные щели S (рис. 4.5).

Рис. 4.5. Метод Юнга наблюдения интерференции
Таким образом, щели S1 и S2 являются источниками когерентных пучков света. Когерентность, естественно, имеет место при условии, что расстояние между щелями 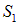 и
и 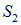 меньше радиуса когерентности света, выходящего из щели
меньше радиуса когерентности света, выходящего из щели  . Интерференционная картина может наблюдаться на экране Э, расположенном на некотором расстоянии от щелей.
. Интерференционная картина может наблюдаться на экране Э, расположенном на некотором расстоянии от щелей.
Бизеркало Френеля
Классическим устройством, позволяющим наблюдать интерференцию света, является бизеркало Френеля (рис. 4.6).
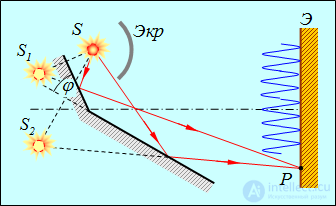
Рис. 4.6. Бизеркало Френеля
Свет, излучаемый источником S, отражается от двух зеркал, расположенных под углом, близким к 180° (угол 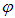 достаточно мал). В результате получаются два световых пучка, которые распространяются от двух мнимых источников S1 и S2, излучения которых, при достаточно малом поперечном размере реального источника
достаточно мал). В результате получаются два световых пучка, которые распространяются от двух мнимых источников S1 и S2, излучения которых, при достаточно малом поперечном размере реального источника 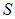 и достаточно малом угле
и достаточно малом угле  , будут когерентными, так как они являются и изображениями одного и того же действительного источника S. При этом лучи, идущие от S1 и S2 к экрану, пройдя различные пути, дают интерференционную картину. (Непрозрачный экран Экр преграждает свету прямой путь от источника S к экрану Э.)
, будут когерентными, так как они являются и изображениями одного и того же действительного источника S. При этом лучи, идущие от S1 и S2 к экрану, пройдя различные пути, дают интерференционную картину. (Непрозрачный экран Экр преграждает свету прямой путь от источника S к экрану Э.)
Бипризма Френеля
Бипризма Френеля представляет собой две одинаковые призмы с малым преломляющим углом, сложенные основаниями так, что образуется общая плоская грань (рис. 4.7).

Рис. 4.7. Бипризма Френеля
Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются когерентные световые пучки, исходящие как бы из двух мнимых источников S1 и S2, как и в случае бизеркала Френеля. Таким образом, на экране происходит наложение когерентных световых пучков и наблюдается интерференционная картина. Выполнение условий когерентности, как и в предыдущих примерах, обеспечивается малыми поперечными размерами реального источника 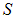 и малостью преломляющего угла бипризмы.
и малостью преломляющего угла бипризмы.
Радужная окраска мыльных пузырей или бензиновых пленок на воде возникает в результате интерференции солнечного света, отраженного двумя поверхностями пленки.
Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом 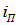 падает плоская монохроматическая волна с длиной
падает плоская монохроматическая волна с длиной 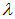 (рис. 4.8).
(рис. 4.8).
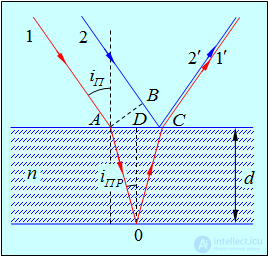
Рис. 4.8. Интерференция света в тонкой пленке
Интерференционная картина в отраженном свете возникает из-за наложения двух волн, отраженных от верхней и нижней поверхностей пленки. Рассмотрим сложение волн, выходящих из точки С. Плоскую волну можно представить как пучок параллельных лучей. Один из лучей пучка (2) непосредственно попадает в точку С и отражается (2')в ней наверх под углом, равным углу падения 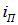 . Другой луч (1) попадает в точку С более сложным путем: сначала он преломляется в точке А и распространяется в пленке, затем отражается от нижней ее поверхности в точке 0 и, наконец, выходит, Преломившись, наружу (1') в точке С под углом, равным углу падения
. Другой луч (1) попадает в точку С более сложным путем: сначала он преломляется в точке А и распространяется в пленке, затем отражается от нижней ее поверхности в точке 0 и, наконец, выходит, Преломившись, наружу (1') в точке С под углом, равным углу падения 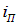 . Таким образом, в точке С пленка отбрасывает вверх два параллельных луча, из которых один образовался за счет отражения от нижней поверхности пленки, второй — вследствие отражения от верхней поверхности пленки. (Пучки, возникающие в результате многократного отражения от поверхностей пленки, не рассматриваются ввиду их малой интенсивности.)
. Таким образом, в точке С пленка отбрасывает вверх два параллельных луча, из которых один образовался за счет отражения от нижней поверхности пленки, второй — вследствие отражения от верхней поверхности пленки. (Пучки, возникающие в результате многократного отражения от поверхностей пленки, не рассматриваются ввиду их малой интенсивности.)
Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
|
|
|
(4.23) |
Полагая показатель преломления воздуха  и учитывая соотношения
и учитывая соотношения
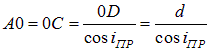
и
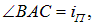
а также
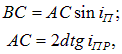
находим
|
|
|
(4.24) |
Используем закон преломления света
|
|
|
(4.25) |
откуда
|
|
|
(4.26) |
Таким образом,
|
|
|
(4.27) |
Кроме оптической разности хода  , следует учесть изменение фазы волны при отражении. В точке С на границе раздела «воздух – пленка» происходит отражение от оптически более плотной среды, то есть среды с большим показателем преломления. При не слишком больших углах падения в этом случае фаза претерпевает изменение на
, следует учесть изменение фазы волны при отражении. В точке С на границе раздела «воздух – пленка» происходит отражение от оптически более плотной среды, то есть среды с большим показателем преломления. При не слишком больших углах падения в этом случае фаза претерпевает изменение на 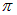 . (Такой же скачок фазы происходит при отражении волны, бегущей вдоль струны, от ее закрепленного конца.) В точке 0 на границе раздела «пленка - воздух» свет отражается от оптически менее плотной среды, так что скачка фазы не происходит.
. (Такой же скачок фазы происходит при отражении волны, бегущей вдоль струны, от ее закрепленного конца.) В точке 0 на границе раздела «пленка - воздух» свет отражается от оптически менее плотной среды, так что скачка фазы не происходит.
В итоге между лучами 1' и 2' возникает дополнительная разность фаз 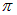 , соответствующая, как следует из формулы (4.12), оптической разности хода
, соответствующая, как следует из формулы (4.12), оптической разности хода  , которую можно учесть, если величину
, которую можно учесть, если величину  уменьшить или увеличить на половину длины волны в вакууме.
уменьшить или увеличить на половину длины волны в вакууме.
Следовательно, при выполнении соотношения
|
|
|
(4.28) |
получается максимум интерференции в отраженном свете, а в случае
|
|
|
(4.29) |
в отраженном свете наблюдается минимум.
Таким образом, при падении света на бензиновую пленку на воде в зависимости от угла зрения и толщины пленки наблюдается радужная окраска пленки, свидетельствующая об усилении световых волн с определенными длинами l. Интерференция в тонких пленках может наблюдаться не только в отраженном, но и в проходящем свете.
Как уже отмечалось, для возникновения наблюдаемой интерференционной картины оптическая разность хода интерферирующих волн не должна превышать длины когерентности  , что накладывает ограничение на толщину пленки.
, что накладывает ограничение на толщину пленки.
Пример. На мыльную пленку (п = 1.3), находящуюся в воздухе, падает по нормали пучок белого света. Определим, при какой наименьшей толщине d пленки отраженный свет с длиной волны 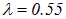 мкм окажется максимально усиленным в результате интерференции.
мкм окажется максимально усиленным в результате интерференции.
Из условия интерференционного максимума (4.28) находим для толщины пленки выражение
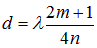
(угол падения 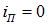 ). Минимальное значение d получается при
). Минимальное значение d получается при 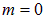 :
:
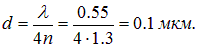
Рассмотрим отражение света от соприкасающихся друг с другом плоско-параллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 4.9). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный клин (зазор) между пластинкой и линзой. (Вследствие большой толщины пластинки и линзы отраженные от других поверхностей волны интерференционных картин не создают.)
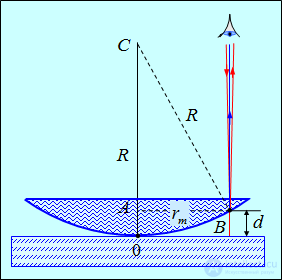
Рис. 4.9. Наблюдение колец Ньютона
При нормальном падении света интерференционная картина имеет вид концентрических окружностей (кольца Ньютона). Каждая из таких интерференционных полос возникает в результате отражения от участков воздушного клина с одинаковой толщиной (вследствие чего их называют интерференционными полосами равной толщины). Определим радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае 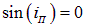 и оптическая разность хода равна (в воздушном зазоре
и оптическая разность хода равна (в воздушном зазоре  ):
):
|
|
|
(4.30) |
Из треугольника 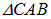 имеем (R>>d):
имеем (R>>d):
|
|
|
(4.31) |
или
|
|
|
(4.32) |
Таким образом, для светлых колец (максимумы) разность хода будет
|
|
|
(4.33) |
Отсюда следует выражение для радиусов светлых колец:
|
|
|
(4.34) |
Радиусы темных колец Ньютона получаются равными
|
|
|
(4.35) |
В точке касания пластинки и линзы, то есть при 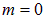 ,
,  , наблюдается минимум интенсивности, обусловленный изменением фазы колебаний на
, наблюдается минимум интенсивности, обусловленный изменением фазы колебаний на 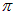 при отражении световой волны от пластинки.
при отражении световой волны от пластинки.
Пример. В отраженном свете с длиной волны 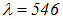 нм были измерены радиусы двух светлых колец Ньютона, оказавшиеся равными 0.161 см и 0.284 см. Было подсчитано, что между этими кольцами расположено 19 других светлых колец. Определим радиус кривизны линзы.
нм были измерены радиусы двух светлых колец Ньютона, оказавшиеся равными 0.161 см и 0.284 см. Было подсчитано, что между этими кольцами расположено 19 других светлых колец. Определим радиус кривизны линзы.
Пусть меньшее измеренное кольцо Ньютона имеет порядок m, тогда порядок большего равен m + 20. Используем (4.34):
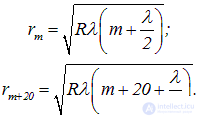
Возводя эти равенства в квадрат и разделив одно на другое, получим
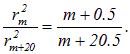
Отсюда находим порядок m меньшего из упомянутых колец Ньютона:
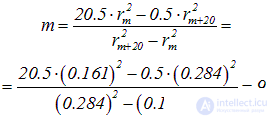
и искомый радиус кривизны линзы будет равен
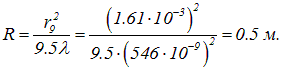
Исследование, описанное в статье про интерференция света, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое интерференция света и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Колебания и волны (Оптика, акустика и радиофизика)
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика