Лекция
Привет, Вы узнаете о том , что такое фракталы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое фракталы, фрактал , настоятельно рекомендую прочитать все из категории Синергетика.
фрактал (лат. fractus — дробленый, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближенно совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференцируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введен Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:
Многие объекты в природе обладают свойствами фрактала, например: побережья, облака, кроны деревьев, снежинки, система кровообращения, альвеолы.
Исследованы отдельные фрактальные структуры - множество Кантора, ковер Серпиньского, снежинка и др. Вводится понятие фрактальной размерности и метод ее расчета. Описано построение множества Мандельброта, и проводится с помощью компьютера его анализ.
I. При возникновении порядока в хаотических системах; сосуществовании хаоса и порядка, перехода от одного к другому; конкуренции или взаимоСОдействии в сложных системах есть общий элемент - конкуренция нескольких центров за доминирование на плоскости или их взаимоСОдействие. Обычно не встречается простой структуры границ, чаще имеет место филигранное переплетение и борьба за свои участки. В этой пограничной области происходит переход от одной формы существования к другой, от порядка к беспорядку и наоборот. Порой возникает третий конкурент, который пользуется разногласиями двух других и насаждает свою область влияния.
II. Математический подход к описанию таких процессов в природе дал в 1980 г. французский математик Бенуа Мандельброт, указавший на фрактальную геометрию природы. Фрактальные объекты самоподобны, т. е. их вид не претерпевает существенных изменений при разглядывании их в микроскоп с любым увеличением. О множествах, имеющих такую структуру, говорят, что они обладают геометрической (масштабной) инвариантностью. Процессы, порождающие такие структуры - это процессы с обратной связью, в которых одна и та же операция выполняется снова и снова. Здесь результат одной итерации является начальным условием для следующей, причем требуется нелинейная зависимость между результатом и начальным значением, т. е. динамический закон xn+1 = f(xn, С) более сложный, чем линейный xn+1 = kxn .
III. Существует важная количественная характеристика фрактальных объектов - дробная размерность. Рассмотрим некоторое множество А и попытаемся полностью покрыть его отрезками, квадратиками или гиперкубами со стороной  . Пусть N - минимальное число кубиков или квадратиков, необходимых для покрытия А. Рассмотрим предел
. Пусть N - минимальное число кубиков или квадратиков, необходимых для покрытия А. Рассмотрим предел
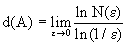 .
.
Величина d(А)=dF называется фрактальной размерностью.

Рис. 1 Покрытие объекта (множества точек) кубами с длинной ребра  :
:
а) одномерный объект, б) двумерное пространство.
Как следует из данной книги, синергетика целенаправленно пытается отыскать правила, по которым возникает порядок в хаотических системах; сосуществование хаоса и порядка, переход от одного к другому; конкуренция или взаимоСОдействие в сложных системах. Эти процессы возникают в различных физических и математических задачах. В них есть общий элемент: конкуренция нескольких центров за доминирование на плоскости или их взаимоСОдействие. Обычно не встречается простой структуры границ, чаще имеет место филигранное переплетение и борьба за свои участки. В этой пограничной области происходит переход от одной формы существования к другой, от порядка к беспорядку и наоборот. Порой возникает третий конкурент, который пользуется разногласиями двух других и насаждает свою область влияния.
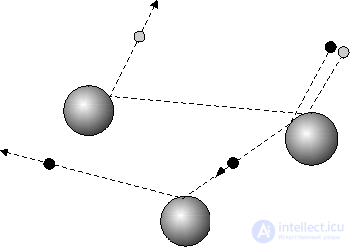
Рис 1. Движение маленького шарика со случайно расположенными большими фиксированными шарами.
Выше отмечалось, что любой нелинейный процесс приводит к ветвлению, к развилке на пути, в которой система может выбрать ту или иную ветвь, но последствия решения невозможно предсказать. Самые незначительные неточности в начальном состоянии системы развиваются, в каждый конкретный момент причинная связь сохраняется, но после нескольких ветвлений она уже не видна. Пример такой системы дает движение с участием жестких шаров, где рассматривается движение маленького шарика, сталкивающегося со случайно расположенными в пространстве большими фиксированными шарами (рис. 1). Если внести малейшую неопределенность в начальные условия, то она будет очень быстро возрастать и делает невозможным предсказание уже после нескольких первых столкновений о местоположении малых шаров. Увеличение точности задания начальных условий потребует бесконечного увеличения информации, иначе придем к необратимости.
Эти трудности, как уже отмечалось, характерны не только для механических задач, они встречаются и в физике элементарных частиц, и в биологии, и в социологии. Требуются новые взгляды в науке, новые концепции [15], новый математический аппарат. Это не означает, что известные до сих пор законы природы неверны, просто мы недостаточно осознаем, что в них скрыто. Математический подход к более широкому взгляду на природу дал в 1980 г. французский математик Бенуа Мандельброт, указавший на фрактальную геометрию природы. Известная нам геометрия неспособна описать форму облака, горы, дерева или берега моря. На приведенном рисунке хорошо видна фрактальная структура кровеносных сосудов сердца. Сравнивая исходное изображение (cверху) и его увеличенный фрагмент (внизу) можно убедится, что топология крупных и мелких сосудов статистически идентична.
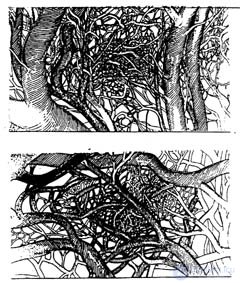
Природа демонстрирует нам совсем иной уровень сложности, связанной с морфологией аморфного. Теперь приведем следующие фракталы "искуственного происхождения":


Не правда ли, очень правдоподобно? Следующий пример - уже научно значимый результат: слева фотография диффузионных каналов в пористой среде, а справа - математическая фрактальная модель этого процесса.
 |
 |
Фрактальные объекты самоподобны, т. е. их вид не претерпевает существенных изменений при разглядывании их в микроскоп с любым увеличением. О множествах, имеющих такую структуру, говорят, что они обладают геометрической (масштабной) инвариантностью. Процессы, порождающие такие структуры - это процессы с обратной связью, в которых одна и та же операция выполняется снова и снова.
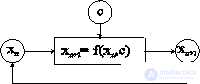
Рис. 2 Схематическая диаграмма динамического процесса xn+1=f(xn, С)
Здесь результат одной итерации является начальным условием для следующей (рис. 2), причем требуется нелинейная зависимость между результатом и начальным значением, т. е. динамический закон xn+1 = f(xn, С) более сложный, чем линейный xn+1 = kxn . Как следует из рис. 2, зависимость xn+1 от xn должна содержать параметр С. Если начать итерационный процесс с некоторого значения x0, то его результатом будет последовательность x1, x2, ... Если исследовать поведение такой последовательности, мы и получим (как правило) какой-либо фрактальный объект. Такие последовательности сильно отличаются от обыных последовательностей в математике. Очередной шаг зависит от предыдущего и случайностей, а не от начального значения. А в жизни чаще всего так и бывает: ваши действия в основном определяются событиями предыдущих дней и отчасти случаем и не зависят от вашего дня рождения (астрологию не трогаем, т.к. за начальное значение с полным правом можно взять любой другой день вашей жизни).
Большинство приведенных в этом параграфе примеры фракталов - "искуственного" происхождения: т.е. Об этом говорит сайт https://intellect.icu . самоподобие в них является правилом построения. Через параграф мы рассмотрим примеры фракталов, возникающих по механизму на рис 2, а далее - как строятся и исследуются фракталы.
Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены первый, второй и четвертый шаги этой процедуры для кривой Коха.
Примерами таких кривых служат:
С помощью похожей процедуры получается дерево Пифагора.
Свойство самоподобия можно математически строго выразить следующим образом. Пусть — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:
Можно показать, что отображение является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.
Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения — отображения подобия, а
— число звеньев генератора.
Для треугольника Серпинского и отображения
,
,
— гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении
.
В случае, когда отображения — преобразования подобия с коэффициентами
, размерность
фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения
. Так, для треугольника Серпинского получаем
.
По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения , мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.
Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задается итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.
Пусть — многочлен,
— комплексное число. Рассмотрим следующую последовательность:
Нас интересует поведение этой последовательности при стремлении к бесконечности. Эта последовательность может:
Множества значений }, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.
Так, множество Жюлиа — множество точек бифуркации для многочлена (или другой похожей функции), то есть тех значений
, для которых поведение последовательности {\displaystyle z_{n}}
может резко меняться при сколь угодно малых изменениях
.
Другой вариант получения фрактальных множеств — введение параметра в многочлен и рассмотрение множества тех значений параметра, при которых последовательность
демонстрирует определенное поведение при фиксированном
. Так, множество Мандельброта — это множество всех
, при которых
для
и
не стремится к бесконечности.
Еще один известный пример такого рода — бассейны Ньютона.
Популярно создание красивых графических образов на основе комплексной динамики путем раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления к бесконечности (определяемой, скажем, как наименьший номер
, при котором
превысит фиксированную большую величину
).
Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:
Природные объекты (квазифракталы) отличаются от идеальных абстрактных фракталов неполнотой и неточностью повторений структуры. Большинство встречающихся в природе фракталоподобных структур (линия берега, деревья, листья растений, кораллы, …) являются квазифракталами, поскольку на некотором малом масштабе фрактальная структура исчезает. Природные структуры не могут быть идеальными фракталами из-за ограничений, накладываемых размерами живой клетки и, в конечном итоге, размерами молекул.
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и тому подобное. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов). После создания кривой Коха было предложено использовать ее при вычислении протяженности береговой линии.
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил ее на лист бумаги, затем присоединил к приемнику.
Коэн основал собственную компанию и наладил серийный выпуск своих антенн. C тех пор теория фрактальных антенн продолжает интенсивно развиваться. Преимуществом таких антенн является многодиапазонность и сравнительная широкополосность.
Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).
Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.
|
Фракталы
|
||
|---|---|---|
| Характеристики |
Фрактальная размерность (Размерность Хаусдорфа · Размерность Лебега) · Рекурсия · Самоподобие
|
|
| Простейшие фракталы |
Папоротник Барнсли · Канторово множество · Кривая дракона · Кривая Коха · Губка Менгера · Ковер Серпинского · Треугольник Серпинского · Заполняющая пространство кривая
|
|
| Странный аттрактор |
Мультифрактал
|
|
| L- система |
Заполняющая пространство кривая
|
|
| Бифуркационные фракталы | ||
| Случайные фракталы | ||
| Люди |
Георг Кантор · Феликс Хаусдорф · Гастон Жюлиа · Хельге фон Кох · Поль Леви · Александр Ляпунов · Бенуа Мандельброт · Льюис Ричардсон · Вацлав Серпинский
|
|
| Связанные темы | ||
Прочтение данной статьи про фракталы позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое фракталы, фрактал и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика
Комментарии
Оставить комментарий
Синергетика
Термины: Синергетика