4.2 Энтропийный насос. Диссипативные структуры

Привет, Вы узнаете о том , что такое энтропийный насос диссипативные структуры, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое энтропийный насос диссипативные структуры , настоятельно рекомендую прочитать все из категории Синергетика.

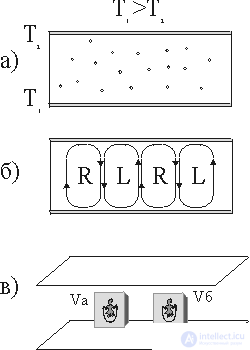Рис. 1 Перенос теплового потока в газе:
а) молекулярный перенос;
б) конвективные токи, вращающиеся по часовой (R) и против часовой (L) стрелок;
в) наблюдатель в объемах V_а и V_б.

В 1901 году физик Бенар обнаружил странный эффект в конвективном движении газа и жидкости. Рассмотрим слой жидкости, подогреваемой снизу (рис. 1,а) при малых значениях произведения чисел Грасгофа Gr и Прандтля Pr (Gr*Pr <10³). (Подробнее о Gr и Pr.) Тепло переносится в результате процесса теплопроводности, т. е. благодаря молекулярной передаче энергии хаотически движущихся молекул газа или жидкости.

Эффект Бенара можно также наблюдать в следующем опыте: в неглубокий сосуд помещают растительное или силиконовое масло и равномерно подогревают его снизу. Возникает разность температур между верхней и нижней поверхностями. При 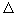 T > 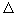 T_кр возникает конвекция и жидкость разбивается на гексагональные ячейки (рис. 2), т. е. возникает динамическая, организованная, упорядоченная структура - это один из видов диссипативной структуры.

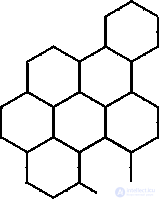
Посмотрим на явления хаоса и порядка с позиции миниатюрного наблюдателя, помещенного в объемы V_А и V_В жидкости (рис. 1,в) в условиях хаотического движения жидкости между пластинами (рис. 1,а).

Наблюдатель строит свои суждения лишь на наблюдениях над окружающей средой, он не сможет определить в каком из двух объемов (V_А или V_В) он находится. Иными словами, все объемы, которые можно выделить в жидкости, будут неразличимы между собою и наблюдателю безразлично, куда его поместят - везде все едино, и у него нет внутренних возможностей воспринять пространство. Если на такую систему оказать возмущение, например, изменить где-то ее температуру, то оно затухает во времени. Это устойчивое состояние. В таком состоянии наблюдатель не в состоянии иметь собственные представления ни о времени, ни о пространстве. Ситуация существенно изменяется, если в системе возникнут конвекционные токи, изображенные на рис. 1,б. Например, наблюдатель может решить, где он находится, наблюдая характер вращения (по часовой R или против часовой L стрелки) в своей ячейке. Подсчитывая количество ячеек, которые он минует, он может получить представление о пространстве: он обнаруживает упорядоченность системы. Иными словами, возникают корреляции между удаленными частями системы, т. е. мы наблюдаем эффект самоорганизации. Обратим внимание на различие между дальнодействующим характером (порядка см и больше) этих корреляций и короткодействующим характером межмолекулярных сил (порядка ангстрем 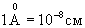 ). Столь сильное различие в масштабах выражает глубокую разницу между равновесным и неравновесным состояниями. Каков же механизм "согласованного действия" молекул на расстояниях, в сотни миллионов раз превышающих расстояния межмолекулярных взаимодействий?

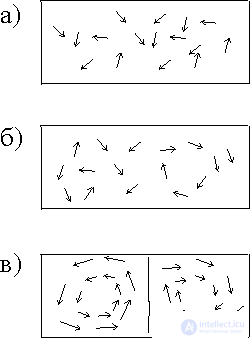Рис 3. Зарождение конвективного движения:
а) хаотическое движение;
б) возникают и разрушаются конвективные ячейки
в) ячейки Бенара.

В 1988 г. было проведено численное моделирование вихрей Бенара: исследовалось 5050 твердых дисков, двигающихся и сталкивающихся в двумерном ящике. Верхняя и нижняя границы ящика поддерживались при различных температурах (диски, сталкиваясь с каждой из сторон, отлетали с новой скоростью, соответствующей температуре стенки). Далее диски были подвержены действию внешней силы, моделирующей силу тяжести (она направлена против gradT). Исходное положение: диски случайно распределены по ящику, как в равновесном состоянии частицы при некоторой температуре Т (рис. 3,а). 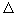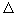Если  Т <  Т_кр (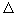 Т_кр связана с критерием К_кр), то наблюдается возникновение в системе малых вихрей, которые вскоре исчезают (рис. Об этом говорит сайт https://intellect.icu . 3,б). При  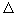T  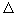 Т_кр и выше вихри не исчезают. Они вовлекают в свое движение все большее число "молекул" до тех пор, пока весь слой жидкости не окажется вовлеченным в вихревое движение (рис. 3,в). Отметим, что такой эксперимент характеризуется высокой воспроизводимостью: при одних и тех же условиях превышение  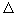Т_кр всегда приводит к появлению конвекционной картины. Однако при этом возможно изменение направления вращения в ячейках. Например, в левой ячейке (рис. 1,б) правое вращение (R) может замениться на левое (L). Итак, как только превысили значение  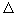Т_кр, совершенно точно появятся конвекционные токи (детерминизм), но направление их вращения непредсказуемо (случайность). Удивительное сотрудничество между случайностью и определенностью. Высказанные соображения представлены на рис. 4: мы видим, что вдали от равновесия система может приспосабливаться к окружению несколькими различными способами, и лишь случай решает, какое из этих решений будет реализовано [3, 6].

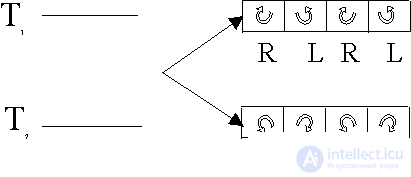
Можно высказать утверждение, что при 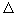 Т =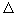 Т_кр появляется неустойчивость процесса: вблизи равновесия второе начало еще гарантирует, что флуктуации затухают и в конце концов вымирают. Равновесные системы контролируются экспериментатором. В неравновесных системах экспериментатор не может управлять спонтанным возникновением вихрей. Неконтролируемые флуктуации могут усиливаться и играть решающую роль.

Итак, неустойчивость означает, что флуктуации могут перестать быть просто "шумом" и превратиться в фактор, направляющий глобальную эволюцию системы. То же событие, та же флуктуация могут быть вполне пренебрежимыми, если система устойчива, и стать весьма существенными для неравновесной системы.

Следует отметить еще одну важную особенность: на рис. 3 представлены результаты осреднения по времени для большого числа столкновений (более миллиона). Если бы сделать мгновенный снимок (рис. 3,б), то можно усмотреть неупорядоченность системы, т. е. не обратить внимание на появление упорядоченных вихрей. Демон, наблюдающий мгновенное состояние картин 3,а и 3,б не смог бы заметить элементов упорядоченности в рис. 3,б. Он видел бы в том и другом случае запутанное движение молекул.

Что произойдет в том случае, когда будет превышен первый порог структурирования 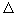 Т = 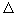 Т_кр1 и разность температур будет дальше возрастать? В некоторой области  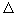T >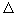 Т_кр1 ячейки Бенара будут существовать, однако, некоторые их характеристики начнут меняться. Затем, после перехода через второе критическое состояние  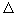Т  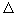 T_кр2 структура течения станет размытой и возникнет новый режим, характеризуемый неупорядоченной зависимостью переменных во времени - это так называемый турбулентный режим.

Выше рассматривался один из множества примеров, когда совокупность частиц превращается в систему, и у нее возникают новые свойства кооперативного взаимодействия, не сводящиеся к свойствам составляющих ее элементов.

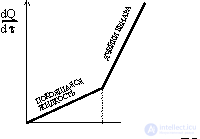
Приведем попытку количественного описания наблюдаемых эффектов. На рис. 5 представлена зависимость потока теплоты dQ/d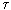 =q Дж/с, Вт от разности температур  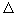Т на пластинах. При  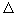Т=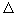 Т_кр происходит резкий излом зависимости dQ/d 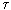и возникает структурообразование. Так как рассматриваемая система обменивается теплотой с окружающей средой, то можно представить общий поток энтропии через поверхность жидкости с помощью формулы (функция диссипации)

 <0

Жидкость в этих условиях экспортирует энтропию. В стационарных условиях этот отток энтропии компенсируется производством энтропии (внутреннее трение, теплопроводность). Как отмечалось выше, такие системы называют диссипативными: открытые, далекие от равновесия, структурообразующие, самоорганизующиеся системы.

Диссипативные системы заставляют по-новому посмотреть на проблему связи второго начала термодинамики и законов классической механики. Машинная имитация динамики соударяющихся частиц с целью проследить судьбу эволюции такой системы была реализована С. И. Яковенко. Им рассмотрена замкнутая система со многими частицами, заданы из классической механики законы взаимодействия частиц, прочие влияния на судьбу системы исключены. Поскольку максимум энтропии соответствует состоянию максимума хаоса, то по характеру движения частиц можно представить себе и действие второго закона в системе частиц. Было выполнено большое число машинных экспериментов, которые привели автора к следующему выводу: состояние максимального хаоса не реализуется само по себе, как следствие эволюции частиц согласно законам классической механики [3].

Далее, С. И. Яковенко обнаружил, что достаточно ввести тем или иным способом некое стохастическое начало, чтобы получить наблюдаемую в природе картину. Иными словами, возможна связь между присущим микромиру статистическим началом и свойством системы, характеризующимся величиной энтропии. А последняя принадлежит макромиру, т. е. у системы появляются свойства, не выводимые из свойств элементов.

Возможно по-новому взглянуть на второе начало термодинамики, как на системный закон: он имеет смысл для большого числа частиц и уже поэтому не выводим из законов механики и законов парных взаимодействий. У совокупности частиц могут возникнуть свойства, отсутствующие у ее отдельных элементов. Системные особенности, по-видимому, появляются на определенном уровне сложности систем, когда последняя теряет устойчивость и движение частиц приобретает хаотический характер. Причиной разрушения порядка служит здесь случайность.

Можно привести много примеров, когда совокупность частиц превращается в систему и у нее возникают новые свойства кооперативного взаимодействия. Мы еще вернемся к этому вопросу в разделе, посвященном социальным явлениям (перейти).

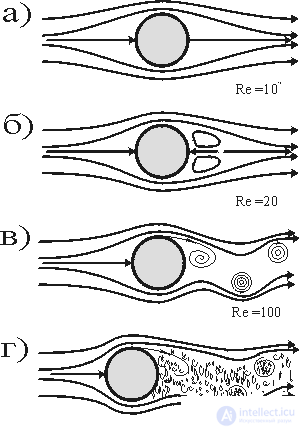
Рис 6. Рождение турбулентности при обтекакании шара потоком жидкости:
а) ламинарное течение (Re=10^-2);
б) появление вихрей в кормовой части (Re=20);
в) развитие вихрей (Re=10²);
г) развитая турбулентность (Re>10⁴).

Рассмотрим цилиндр, ось которого перпендикулярна скорости V движущейся жидкости. На рис. 6,а) схематически показаны линии тока жидкости при малой скорости ее движения. Характер этих линий зависит не только от скорости, но и от кинематической вязкости 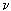 =  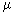/ ( 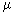- вязкость жидкости,  - ее плотность) и от диаметра d цилиндра. Эти числа объединяют в безразмерный комплекс Рейнольдса, Re=Vd/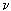 , который более полно, чем одна скорость описывает картину обтекания цилиндра жидкостью. Итак, при малых числах Re  20 линии тока стационарны, т. е. не меняются со временем. Но после того, как скорость превысит некий порог, появляются рециркуляционные вихри в следе за цилиндром (рис. 6,б). Стационарный режим исчезает, уступая место цепочке вихрей, вращающихся попеременно то в одну, то в другую сторону. Это явление носит название вихревой дорожки Бенера- Кармана. На рис. 6 изображена эволюция вихрей для различных значений 20  Re  10⁶. При Re > 20 появляется пара вихрей, при Re > 10² вихри осциллируют. При еще более высокой скорости (Re > 10⁶) появляется нерегулярная картина - турбулентный поток. В последней можно также усмотреть появление новой картины самоорганизации - порядка в хаосе.

Подчеркнем универсальный характер описываемых здесь периодических явлений: след Бенара- Кармана можно обнаружить в структуре облаков, создаваемых ветром над городом и за Большим красным пятном на Юпитере.

Прочтение данной статьи про энтропийный насос диссипативные структуры позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое энтропийный насос диссипативные структуры и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика