6.3 Мера информации по Шеннону Примеры

Привет, Вы узнаете о том , что такое мера информации по шеннону ы , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое мера информации по шеннону ы , настоятельно рекомендую прочитать все из категории Синергетика.

Пример 1

Рассмотрим дискретную случайную величину и будем понимать под испытанием получение ее очередного значения. Попробуем прогнозировать результат испытания, т. е. предсказать значение, которое примет случайная величина. Конечно в силу случайности рассматриваемой величины исход испытания несет в себе некоторую неопределенность, но, зная закон распределения, мы можем пытаться в какой-то степени оценить надежность прогноза.

Естественно пытаться использовать для этой цели наиболее уже известные из курса теории вероятностей и математической статистики математические ожидания (M(X)) и дисперсии (D(X)):

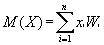
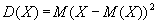
Однако оказывается, что для прогнозирования значения случайной величины эти характеристики могут оказаться бесполезными. В этом можно убедиться на следующем примере.

Пусть заданы две случайные величины, обладающие следующими законами распределения:

x 0 1 W 0.5 0.5

y 1/3 2 W 0.9 0.1

Найдем их математические ожидания и дисперсии:

M(x) = 0*1/2 + 1*1/2 = 1/2,

M(y) = 1/3*0.9 + 2*0.1 = 1/2.

Таким образом, математические ожидания этих случайных величин совпадают. Об этом говорит сайт https://intellect.icu . То же относится и к дисперсиям.

Действительно,

D(x) = 0²*1/2 + 1²*1/2 - 0.25= 0.25,

D(x) = 1/3²*0.9 + 2²*0.1 - 0.25= 0.25.

Однако интуитивно ясно, что закон распределения y несет в себе значительно меньшую неопределенность и позволяет с довольно большой надежностью предсказать, что результатом испытания будет значение y = 1/3. Следовательно, ни математическое ожидание, ни дисперсия в качестве меры неопределенности распределения использованы быть не могут.

Подсчитаем по формуле (5) энтропию приведенных выше распределений. Для удобства подсчета логарифмы будем считать натуральными.

Для случайной величины x получаем

I = -2*0.5*ln 0.5 = 0.6931;

энтропия распределения y равна

I = -0.9*ln 0.9 - 0.1*ln 0.1 = 0.1054*0.9 + 2.3026*0.1 = 0.3251,

т. е. энтропия распределения x более чем вдвое превосходит энтропию распределения y. Это соотношение вполне согласуется с интуитивным представлением о неопределенности имеющихся распределений.

Пример 2

Вероятность наступления события при одном испытании равна W. При каком W результат испытания обладает наибольшей неопределенностью.

Если случайная величина есть число наступлений события в данном испытании, то она описывается схемой

x	0	1
W	1-W	W

Согласно формуле (5) энтропия этой схемы равна

I = - (1-W)*ln (1-W) - W*ln W.

Для удобства вычислений примем, что логарифмы берутся натуральными и найдем максимум этой функции:

dI/dW = ln (1 - W) + 1 - ln W - 1 = ln (1-W) - ln W.

Приравнивая dI/dW к нулю, находим ln (1-W) = ln W, откуда W = 1 - W = 1/2. Так как

то ясно, что при W = 1/2 величина I имеет максимум. 

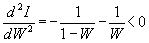
Прочтение данной статьи про мера информации по шеннону ы позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое мера информации по шеннону ы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика

Из статьи мы узнали кратко, но содержательно про мера информации по шеннону ы