7.3 Множество Мандельброта кратко

Привет, Вы узнаете о том , что такое множество мандельброта, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое множество мандельброта, множество жюлиа , настоятельно рекомендую прочитать все из категории Синергетика.

Выше был рассмотрен один из путей построения фракталов - последовательные операции построения подобных элементов. Теперь перейдем к фракталам, возникающим согласно схеме из §7.1.

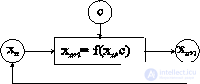
Рис. 1 Схематическая диаграмма динамического процесса x_n+1=f(x_n, С)

В 1980 г. Бенуа Мандельброт обнаружил универсальное множество, теперь носящее его имя. Мандельброт вместо действительных чисел рассмотрел комплексные и наблюдал процесс х₀ х₁ х₂ не на прямой, а в плоскости. Процесс Мандельброта осуществляется по формуле

х_n+1=f(х_n)=х_n +C, C = а + bi,

т. е. выбираем произвольное число х₀, возводим его в квадрат, прибавляем константу С и получаем х₁; затем повторяем для х₂, х₃ и т. д.

Положим С = 0, тогда х₀ 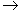х₀² 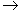х₀⁴ 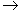х₀⁸ и эта последовательность имеет три возможности:

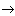• числа становятся все меньше и их последовательность стремится к нулю, т.е. нуль становится аттрактором для процесса х х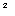 . Об этом говорит сайт https://intellect.icu . Все точки, лежащие на расстоянии меньше 1 от аттрактора движутся к нему.
• числа становятся все больше и стремятся к бесконечности, которая является аттрактором для этого процесса. Все точки, лежащие на расстоянии больше 1 от нуля, идут к бесконечности.
• точки находятся на расстоянии 1 от нуля, их последовательности образуют окружность единичного радиуса.

Плоскость делится на две зоны влияния, а граница - окружность.

Сюрпризы начинаются, когда выберем ненулевое значение С = а + bi. Ниже изображено множество мандельброта (ММ) для процесса х х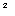 +C ,где показана часть комплексной С-области: - 2,25 < Re C < 0,75, - 1,5 < Im C < 1,5. Фигура отражает соответствие различным значениям параметра С различных типов границ на комплексной С-плоскости. Обозначим черным цветом область значений С, где последовательность ограничена, а белым - экспоненциальное расхождение.

Рис. 2 Множество Мандельброта и его увеличенный фрагмент "в чистом виде"

Видно, что с выходом на комплексную плоскость получаем более полную картину по сравнению с анализом на действительной оси. Различный выбор комплексного числа С приводит к разнообразным конфигурациям. На простом черно-белом изображении не видно такого богатства форм. Сложную динамическую структуру можно отразить только в цвете.

Рис. 3 Эквипотенциальные поверхности вокруг множества Мандельброта.

с

Опишем, как происходит раскрашивание окрестности ММ. Пусть множество изготовлено из металла и несет на себе электрический заряд, тогда поверхность имеет постоянный электрический потенциал, например, 1000 В. В области, окружающей проводник, потенциал падает до нуля. Можно построить эквипотенциальные линии, окружающие ММ. Например, линия, отвечающая потенциалу 1 В, настолько далека от ММ, что выглядит почти как окружность, а линия 900 В напоминает форму ММ и т. д. Раскраска рисунков соответствует этим линиям: разные цвета дают контурную карту электростатического потенциала между ММ и бесконечностью. С ММ тесно связан еще один фрактал - множество жюлиа .

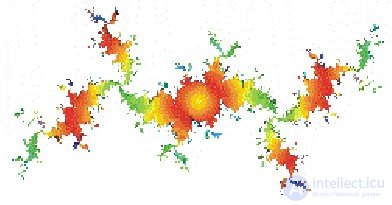
Рис. 4 Множество Жюлиа

Если в ММ Х₀=const=0, а параметр С - комплексная координата точки, на которой выпоняется построение; то в множестве Жюлиа С=const, задаваемая заранее, а плоскость построения - плоскость возможных начальных значений Х₀. Существует много программ, которые строят рассматриваемые фракталы, подробнее об этом можно узнать на домашней страничке авторов. Трудно поверить, но формула х х +C содержит в себе массу структур. Само множество ММ проявляется снова и снова, различных размеров, но всегда одной и той же формы.Это напоминает генетическую организацию высших организмов: каждая клетка содержит полный геном, совокупность всех форм проявления, но в любой точке организма проявляется только некоторая малая часть этих форм.

Вау!! 😲 Ты еще не читал? Это зря!

• Бифуркационные фракталы
• Фрактал Ляпунова
• Бассейны Ньютона

Прочтение данной статьи про множество мандельброта позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое множество мандельброта, множество жюлиа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика